16.2 Two One-Sided Tests Equivalence Testing
The Two One-Sided Tests (TOST) procedure is a method used in equivalence testing to determine whether a population effect size falls within a range of practical equivalence.
Unlike traditional null hypothesis significance testing (NHST), which focuses on detecting differences, TOST tests for similarity by checking whether an effect is small enough to be practically insignificant.
16.2.1 When to Use TOST?
- Bioequivalence Testing
- Example: Determining whether a generic drug is equivalent to a brand-name drug in terms of effectiveness.
- Non-Inferiority Testing
- Example: Assessing whether a new teaching method is not worse than a traditional method by a meaningful margin.
- Equivalence in Business & Finance
- Example: Comparing the performance of two financial models to determine if they produce practically the same results.
- Psychological & Behavioral Research
- Example: Determining whether a new intervention is equally effective as an existing one.
In traditional hypothesis testing, we assess:
\[ H_0: \theta = \theta_0 \quad vs. \quad H_a: \theta \neq \theta_0 \]
where \(\theta\) is a population parameter (e.g., mean difference, regression coefficient, or effect size).
However, in equivalence testing, we are interested in whether \(\theta\) falls within a predefined equivalence margin (\(-\Delta, \Delta\)).
This leads to the TOST procedure, where we conduct two one-sided tests:
1st One-Sided Test:
\[ H_0: \theta \leq -\Delta \quad vs. \quad H_a: \theta > -\Delta \]
2nd One-Sided Test:
\[ H_0: \theta \geq \Delta \quad vs. \quad H_a: \theta < \Delta \]
If both null hypotheses are rejected, then we conclude equivalence (i.e., \(\theta\) is within the equivalence range).
16.2.2 Interpretation of the TOST Procedure
- If the p-value for both one-sided tests is less than \(\alpha\), then we conclude that the effect size falls within the equivalence bounds.
- If one or both p-values are greater than \(\alpha\), we fail to reject the null hypothesis and cannot claim equivalence.
- The TOST procedure provides stronger evidence of similarity than traditional NHST, which only assesses whether an effect is statistically different from zero rather than practically insignificant.
16.2.3 Relationship to Confidence Intervals
Another way to interpret TOST is through confidence intervals (CIs):
- If the entire \((1 - 2\alpha) \times 100\%\) confidence interval lies within \([-\Delta, \Delta]\), we conclude equivalence.
- If the confidence interval extends beyond the equivalence range, we fail to establish equivalence.
This relationship ensures that TOST is consistent with CI-based inference.
16.2.4 Example 1: Testing the Equivalence of Two Means
Suppose we have two groups and want to test whether their mean difference is practically insignificant within a range of \([-0.5, 0.5]\).
library(TOSTER)
# Simulated data: Two groups with similar means
set.seed(123)
group1 <- rnorm(30, mean = 5, sd = 1)
group2 <- rnorm(30, mean = 5.1, sd = 1)# Perform TOST equivalence test
TOSTtwo(
m1 = mean(group1),
sd1 = sd(group1),
n1 = length(group1),
m2 = mean(group2),
sd2 = sd(group2),
n2 = length(group2),
low_eqbound = -0.5,
high_eqbound = 0.5,
alpha = 0.05
)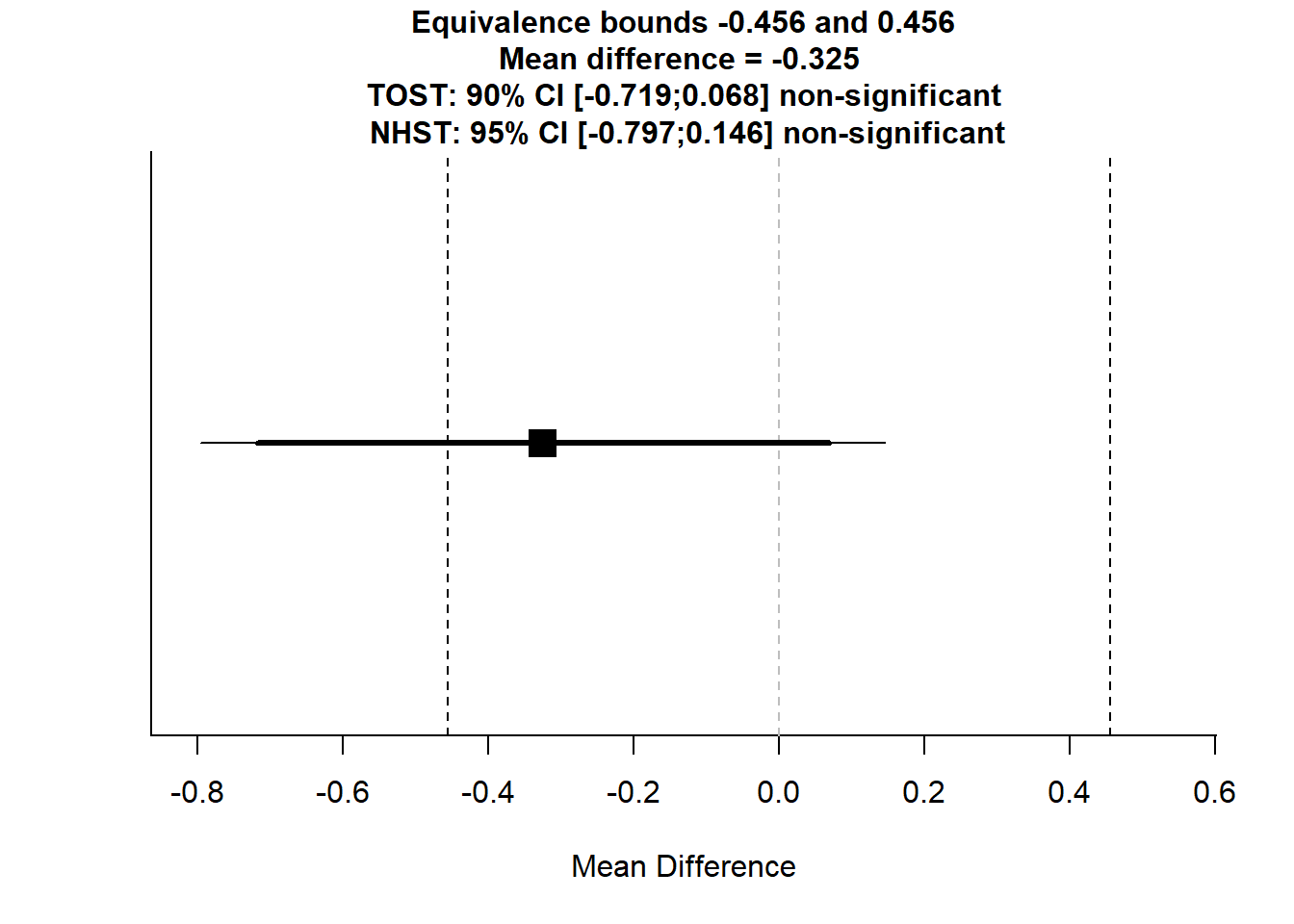
Figure 16.2: Mean Difference Analysis
#> TOST results:
#> t-value lower bound: 0.553 p-value lower bound: 0.291
#> t-value upper bound: -3.32 p-value upper bound: 0.0008
#> degrees of freedom : 56.56
#>
#> Equivalence bounds (Cohen's d):
#> low eqbound: -0.5
#> high eqbound: 0.5
#>
#> Equivalence bounds (raw scores):
#> low eqbound: -0.4555
#> high eqbound: 0.4555
#>
#> TOST confidence interval:
#> lower bound 90% CI: -0.719
#> upper bound 90% CI: 0.068
#>
#> NHST confidence interval:
#> lower bound 95% CI: -0.797
#> upper bound 95% CI: 0.146
#>
#> Equivalence Test Result:
#> The equivalence test was non-significant, t(56.56) = 0.553, p = 0.291, given equivalence bounds of -0.456 and 0.456 (on a raw scale) and an alpha of 0.05.
#>
#> Null Hypothesis Test Result:
#> The null hypothesis test was non-significant, t(56.56) = -1.384, p = 0.172, given an alpha of 0.05.If both p-values are less than 0.05, we conclude that the groups are equivalent within the given range.
The confidence interval helps visualize whether the effect size falls entirely within \([-0.5, 0.5]\).
16.2.4.1 Example 2: TOST for Correlation Equivalence
We can also use TOST to test whether a correlation coefficient is effectively zero.
# Simulated correlation data
set.seed(123)
x <- rnorm(50)
y <- x * 0.02 + rnorm(50, sd = 1) # Very weak correlation# TOST for correlation
TOSTr(
n = length(x),
r = cor(x, y),
low_eqbound_r = -0.1,
high_eqbound_r = 0.1,
alpha = 0.05
)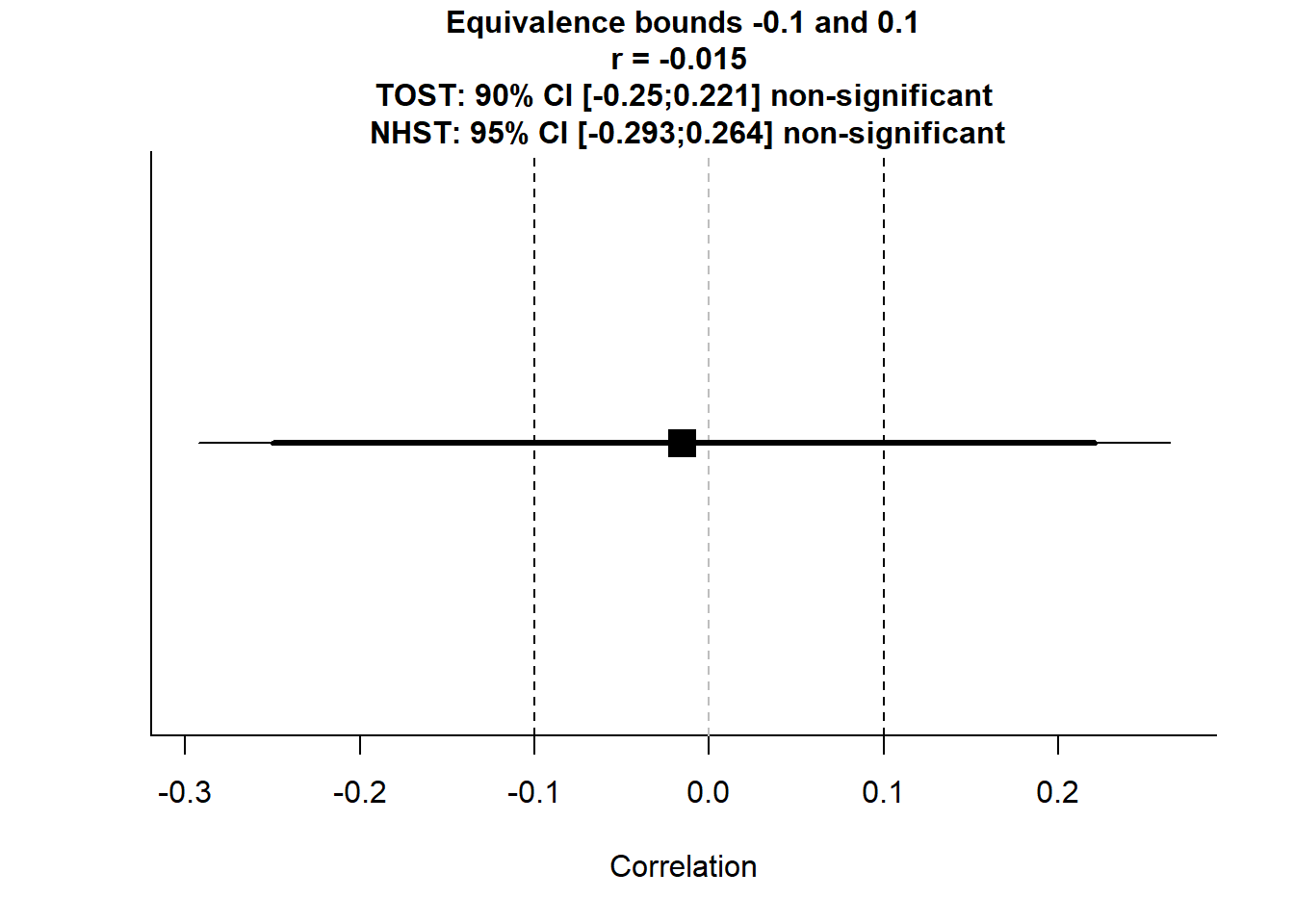
Figure 16.3: Equivalence Bounds
#> TOST results:
#> p-value lower bound: 0.280
#> p-value upper bound: 0.214
#>
#> Equivalence bounds (r):
#> low eqbound: -0.1
#> high eqbound: 0.1
#>
#> TOST confidence interval:
#> lower bound 90% CI: -0.25
#> upper bound 90% CI: 0.221
#>
#> NHST confidence interval:
#> lower bound 95% CI: -0.293
#> upper bound 95% CI: 0.264
#>
#> Equivalence Test Result:
#> The equivalence test was non-significant, p = 0.280, given equivalence bounds of -0.100 and 0.100 and an alpha of 0.05.
#>
#> Null Hypothesis Test Result:
#> The null hypothesis test was non-significant, p = 0.915, given an alpha of 0.05.This tests whether the correlation is within \([-0.1, 0.1]\), meaning “practically zero”.
If both p-values are significant, we conclude that the correlation is effectively negligible.
16.2.5 Advantages of TOST Equivalence Testing
Avoids Misinterpretation of Non-Significance
Traditional NHST failing to reject \(H_0\) does not imply equivalence.
TOST explicitly tests for equivalence, preventing misinterpretation.
Aligned with Confidence Intervals
- TOST conclusions align with confidence interval-based reasoning.
Applicable to Various Statistical Tests
- Can be used for means, correlations, regression coefficients, and more.
Commonly Used in Regulatory & Clinical Studies
- Required for bioequivalence trials by organizations like the FDA (Schuirmann 1987).
16.2.6 When Not to Use TOST
If your research question is about detecting a difference rather than establishing equivalence.
If the equivalence bounds are too wide to be meaningful in practice.
If the sample size is too small, making it difficult to detect equivalence reliably.
| Feature | Traditional NHST | TOST Equivalence Testing |
|---|---|---|
| Null Hypothesis | \(H_0\): No effect (\(\theta = 0\)) | \(H_0\): Effect is outside equivalence bounds |
| Alternative Hypothesis | \(H_a\): There is an effect (\(\theta \neq 0\)) | \(H_a\): Effect is within equivalence bounds |
| Goal | Detect difference | Establish similarity |
| p-value Interpretation | Small \(p\) means evidence for an effect | Small \(p\) means evidence for equivalence |