7.7 Multinomial Logistic Regression
When dealing with categorical response variables with more than two possible outcomes, the multinomial logistic regression is a natural extension of the binary logistic model.
7.7.1 The Multinomial Distribution
Suppose we have a categorical response variable \(Y_i\) that can take values in \(\{1, 2, \dots, J\}\). For each observation \(i\), the probability that it falls into category \(j\) is given by:
\[ p_{ij} = P(Y_i = j), \quad \text{where} \quad \sum_{j=1}^{J} p_{ij} = 1. \]
The response follows a multinomial distribution:
\[ Y_i \sim \text{Multinomial}(1; p_{i1}, p_{i2}, ..., p_{iJ}). \]
This means that each observation belongs to exactly one of the \(J\) categories.
7.7.2 Modeling Probabilities Using Log-Odds
We cannot model the probabilities \(p_{ij}\) directly because they must sum to 1. Instead, we use a logit transformation, comparing each category \(j\) to a baseline category (typically the first category, \(j=1\)):
\[ \eta_{ij} = \log \frac{p_{ij}}{p_{i1}}, \quad j = 2, \dots, J. \]
Using a linear function of covariates \(\mathbf{x}_i\), we define:
\[ \eta_{ij} = \mathbf{x}_i' \beta_j = \beta_{j0} + \sum_{p=1}^{P} \beta_{jp} x_{ip}. \]
Rearranging to express probabilities explicitly:
\[ p_{ij} = p_{i1} \exp(\mathbf{x}_i' \beta_j). \]
Since all probabilities must sum to 1:
\[ p_{i1} + \sum_{j=2}^{J} p_{ij} = 1. \]
Substituting for \(p_{ij}\):
\[ p_{i1} + \sum_{j=2}^{J} p_{i1} \exp(\mathbf{x}_i' \beta_j) = 1. \]
Solving for \(p_{i1}\):
\[ p_{i1} = \frac{1}{1 + \sum_{j=2}^{J} \exp(\mathbf{x}_i' \beta_j)}. \]
Thus, the probability for category \(j\) is:
\[ p_{ij} = \frac{\exp(\mathbf{x}_i' \beta_j)}{1 + \sum_{l=2}^{J} \exp(\mathbf{x}_i' \beta_l)}, \quad j = 2, \dots, J. \]
This formulation is known as the multinomial logit model.
7.7.3 Softmax Representation
An alternative formulation avoids choosing a baseline category and instead treats all \(J\) categories symmetrically using the softmax function:
\[ P(Y_i = j | X_i = x) = \frac{\exp(\beta_{j0} + \sum_{p=1}^{P} \beta_{jp} x_p)}{\sum_{l=1}^{J} \exp(\beta_{l0} + \sum_{p=1}^{P} \beta_{lp} x_p)}. \]
This representation is often used in neural networks and general machine learning models.
7.7.4 Log-Odds Ratio Between Two Categories
The log-odds ratio between two categories \(k\) and \(k'\) is:
\[ \log \frac{P(Y = k | X = x)}{P(Y = k' | X = x)} = (\beta_{k0} - \beta_{k'0}) + \sum_{p=1}^{P} (\beta_{kp} - \beta_{k'p}) x_p. \]
This equation tells us that:
- If \(\beta_{kp} > \beta_{k'p}\), then increasing \(x_p\) increases the odds of choosing category \(k\) over \(k'\).
- If \(\beta_{kp} < \beta_{k'p}\), then increasing \(x_p\) decreases the odds of choosing \(k\) over \(k'\).
7.7.5 Estimation
To estimate the parameters \(\beta_j\), we use Maximum Likelihood estimation.
Given \(n\) independent observations \((Y_i, X_i)\), the likelihood function is:
\[ L(\beta) = \prod_{i=1}^{n} \prod_{j=1}^{J} p_{ij}^{Y_{ij}}. \]
Taking the log-likelihood:
\[ \log L(\beta) = \sum_{i=1}^{n} \sum_{j=1}^{J} Y_{ij} \log p_{ij}. \]
Since there is no closed-form solution, numerical methods (see Non-linear Least Squares Estimation) are used for estimation.
7.7.6 Interpretation of Coefficients
- Each \(\beta_{jp}\) represents the effect of \(x_p\) on the log-odds of category \(j\) relative to the baseline.
- Positive coefficients mean increasing \(x_p\) makes category \(j\) more likely relative to the baseline.
- Negative coefficients mean increasing \(x_p\) makes category \(j\) less likely relative to the baseline.
7.7.7 Application: Multinomial Logistic Regression
1. Load Necessary Libraries and Data
library(faraway) # For the dataset
library(dplyr) # For data manipulation
library(ggplot2) # For visualization
library(nnet) # For multinomial logistic regression
# Load and inspect data
data(nes96, package="faraway")
head(nes96, 3)
#> popul TVnews selfLR ClinLR DoleLR PID age educ income vote
#> 1 0 7 extCon extLib Con strRep 36 HS $3Kminus Dole
#> 2 190 1 sliLib sliLib sliCon weakDem 20 Coll $3Kminus Clinton
#> 3 31 7 Lib Lib Con weakDem 24 BAdeg $3Kminus ClintonThe dataset nes96 contains survey responses, including political party identification (PID), age (age), and education level (educ).
2. Define Political Strength Categories
We classify political strength into three categories:
Strong: Strong Democrat or Strong Republican
Weak: Weak Democrat or Weak Republican
Neutral: Independents and other affiliations
# Check distribution of political identity
table(nes96$PID)
#>
#> strDem weakDem indDem indind indRep weakRep strRep
#> 200 180 108 37 94 150 175
# Define Political Strength variable
nes96 <- nes96 %>%
mutate(Political_Strength = case_when(
PID %in% c("strDem", "strRep") ~ "Strong",
PID %in% c("weakDem", "weakRep") ~ "Weak",
PID %in% c("indDem", "indind", "indRep") ~ "Neutral",
TRUE ~ NA_character_
))
# Summarize
nes96 %>% group_by(Political_Strength) %>% summarise(Count = n())
#> # A tibble: 3 × 2
#> Political_Strength Count
#> <chr> <int>
#> 1 Neutral 239
#> 2 Strong 375
#> 3 Weak 3303. Visualizing Political Strength by Age
We visualize the proportion of each political strength category across age groups.
# Prepare data for visualization
Plot_DF <- nes96 %>%
mutate(Age_Grp = cut_number(age, 4)) %>%
group_by(Age_Grp, Political_Strength) %>%
summarise(count = n(), .groups = 'drop') %>%
group_by(Age_Grp) %>%
mutate(etotal = sum(count), proportion = count / etotal)
# Plot age vs political strength
Age_Plot <- ggplot(
Plot_DF,
aes(
x = Age_Grp,
y = proportion,
group = Political_Strength,
linetype = Political_Strength,
color = Political_Strength
)
) +
geom_line(size = 2) +
labs(title = "Political Strength by Age Group",
x = "Age Group",
y = "Proportion")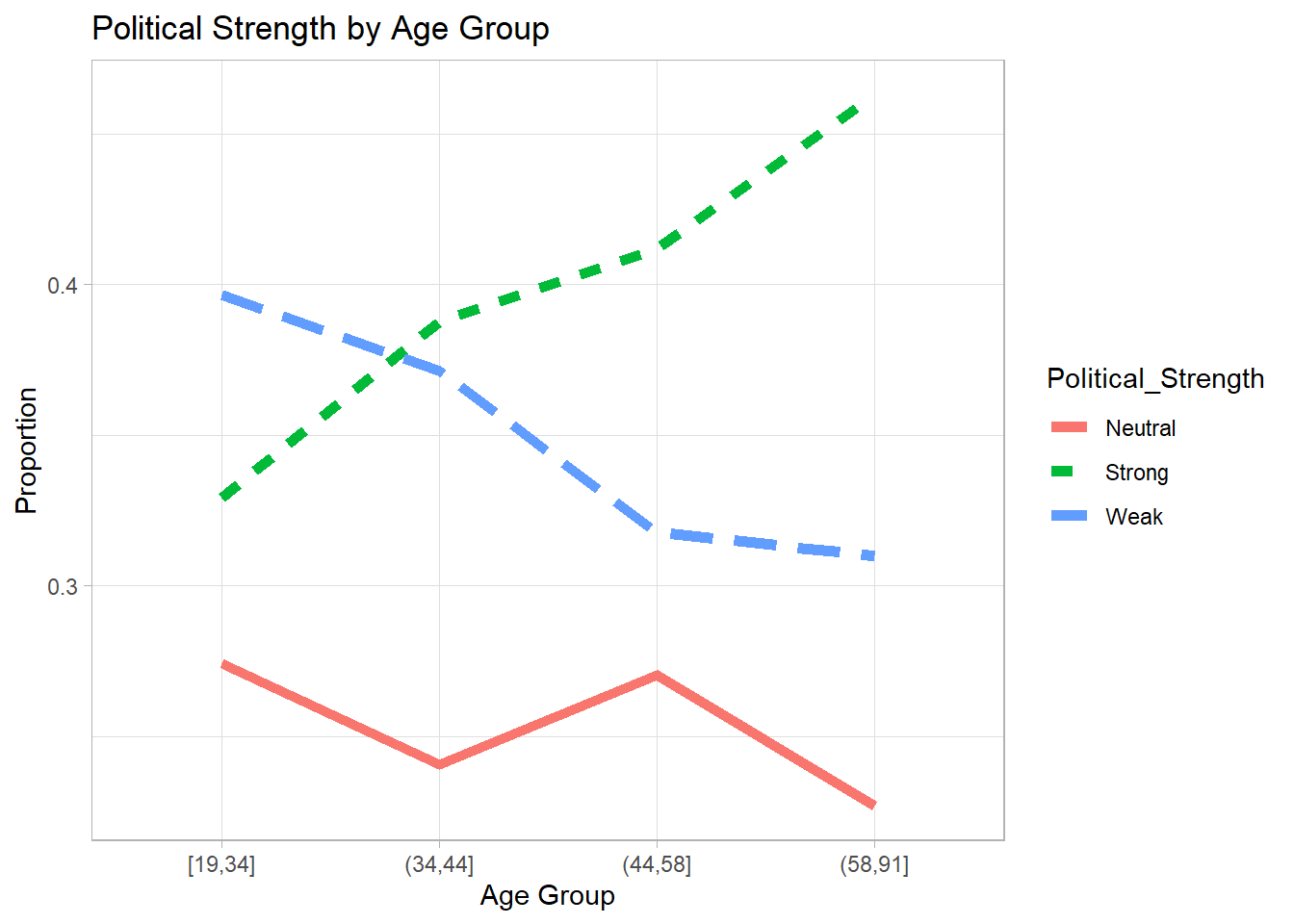
Figure 7.9: Political Strength by Age Group
4. Fit a Multinomial Logistic Model
We model political strength as a function of age and education.
# Fit multinomial logistic regression
Multinomial_Model <-
multinom(Political_Strength ~ age + educ,
data = nes96,
trace = FALSE)
summary(Multinomial_Model)
#> Call:
#> multinom(formula = Political_Strength ~ age + educ, data = nes96,
#> trace = FALSE)
#>
#> Coefficients:
#> (Intercept) age educ.L educ.Q educ.C educ^4
#> Strong -0.08788729 0.010700364 -0.1098951 -0.2016197 -0.1757739 -0.02116307
#> Weak 0.51976285 -0.004868771 -0.1431104 -0.2405395 -0.2411795 0.18353634
#> educ^5 educ^6
#> Strong -0.1664377 -0.1359449
#> Weak -0.1489030 -0.2173144
#>
#> Std. Errors:
#> (Intercept) age educ.L educ.Q educ.C educ^4
#> Strong 0.3017034 0.005280743 0.4586041 0.4318830 0.3628837 0.2964776
#> Weak 0.3097923 0.005537561 0.4920736 0.4616446 0.3881003 0.3169149
#> educ^5 educ^6
#> Strong 0.2515012 0.2166774
#> Weak 0.2643747 0.2199186
#>
#> Residual Deviance: 2024.596
#> AIC: 2056.5965. Stepwise Model Selection Based on AIC
We perform stepwise selection to find the best model.
Multinomial_Step <- step(Multinomial_Model, trace = 0)
#> trying - age
#> trying - educ
#> trying - age
Multinomial_Step
#> Call:
#> multinom(formula = Political_Strength ~ age, data = nes96, trace = FALSE)
#>
#> Coefficients:
#> (Intercept) age
#> Strong -0.01988977 0.009832916
#> Weak 0.59497046 -0.005954348
#>
#> Residual Deviance: 2030.756
#> AIC: 2038.756Compare the best model to the full model based on deviance:
pchisq(
q = deviance(Multinomial_Step) - deviance(Multinomial_Model),
df = Multinomial_Model$edf - Multinomial_Step$edf,
lower.tail = FALSE
)
#> [1] 0.9078172A non-significant p-value suggests no major difference between the full and stepwise models.
6. Predictions & Visualization
Predicting Political Strength Probabilities by Age
# Create data for prediction
PlotData <- data.frame(age = seq(from = 19, to = 91))
# Get predicted probabilities
Preds <- PlotData %>%
bind_cols(data.frame(predict(Multinomial_Step,
PlotData,
type = "probs")))# Plot predicted probabilities across age
plot(
x = Preds$age,
y = Preds$Neutral,
type = "l",
ylim = c(0.2, 0.6),
col = "black",
ylab = "Proportion",
xlab = "Age"
)
lines(x = Preds$age,
y = Preds$Weak,
col = "blue")
lines(x = Preds$age,
y = Preds$Strong,
col = "red")
legend(
"topleft",
legend = c("Neutral", "Weak", "Strong"),
col = c("black", "blue", "red"),
lty = 1
)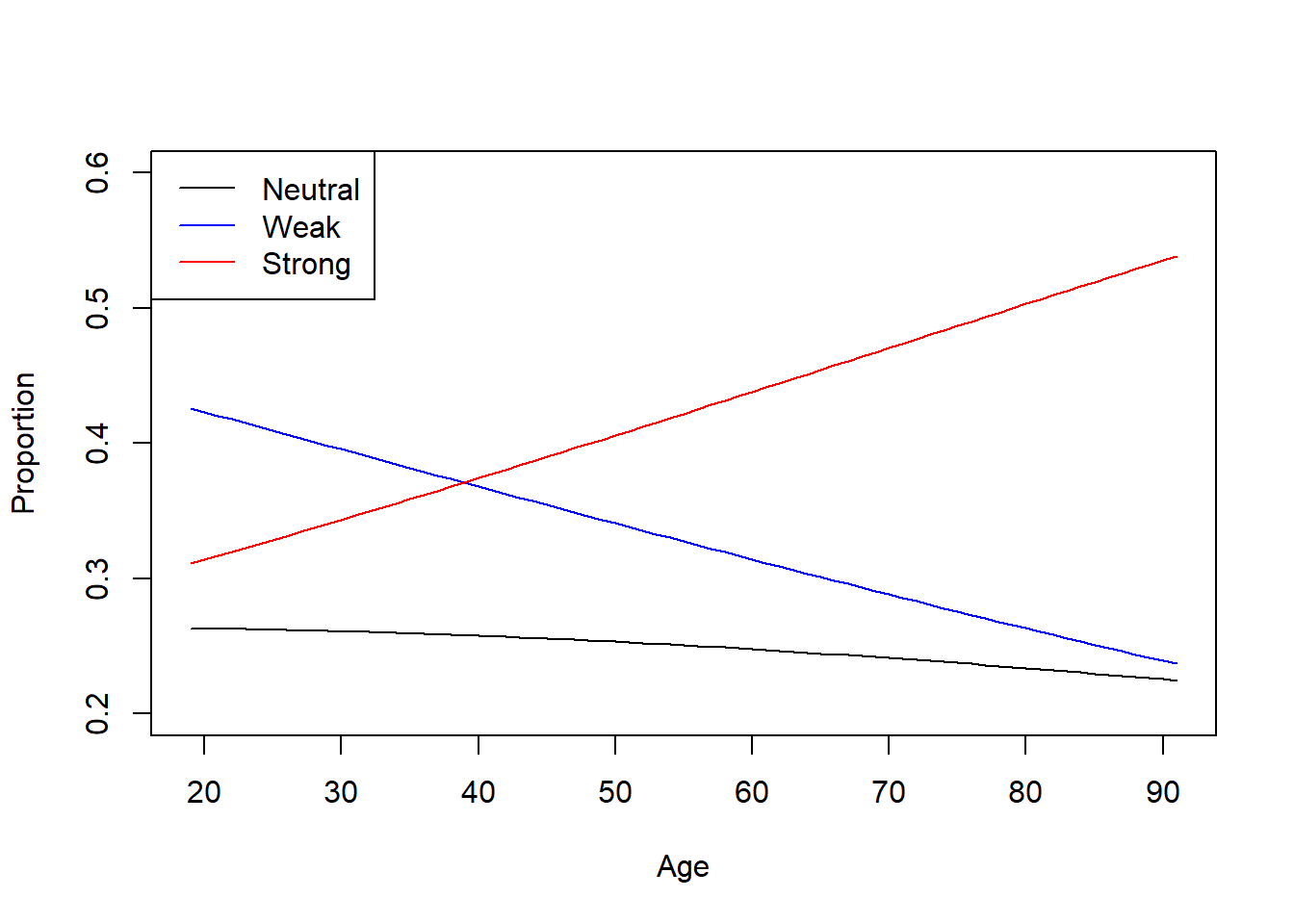
Figure 7.10: Age Group by Predicted Probabilities
Predict for Specific Ages
# Predict class for a 34-year-old
predict(Multinomial_Step, data.frame(age = 34))
#> [1] Weak
#> Levels: Neutral Strong Weak
# Predict probabilities for 34 and 35-year-olds
predict(Multinomial_Step,
data.frame(age = c(34, 35)),
type = "probs")
#> Neutral Strong Weak
#> 1 0.2597275 0.3556910 0.3845815
#> 2 0.2594080 0.3587639 0.38182817.7.8 Application: Gamma Regression
When response variables are strictly positive, we use Gamma regression.
1. Load and Prepare Data
library(agridat) # Agricultural dataset
library(ggplot2)
# Load and filter data
dat <- agridat::streibig.competition
gammaDat <- subset(dat, sseeds < 1) # Keep only barley
gammaDat <-
transform(gammaDat,
x = bseeds,
y = bdwt,
block = factor(block))2. Visualization of Inverse Yield
ggplot(gammaDat, aes(x = x, y = 1 / y)) +
geom_point(aes(color = block, shape = block)) +
labs(title = "Inverse Yield vs Seeding Rate",
x = "Seeding Rate",
y = "Inverse Yield")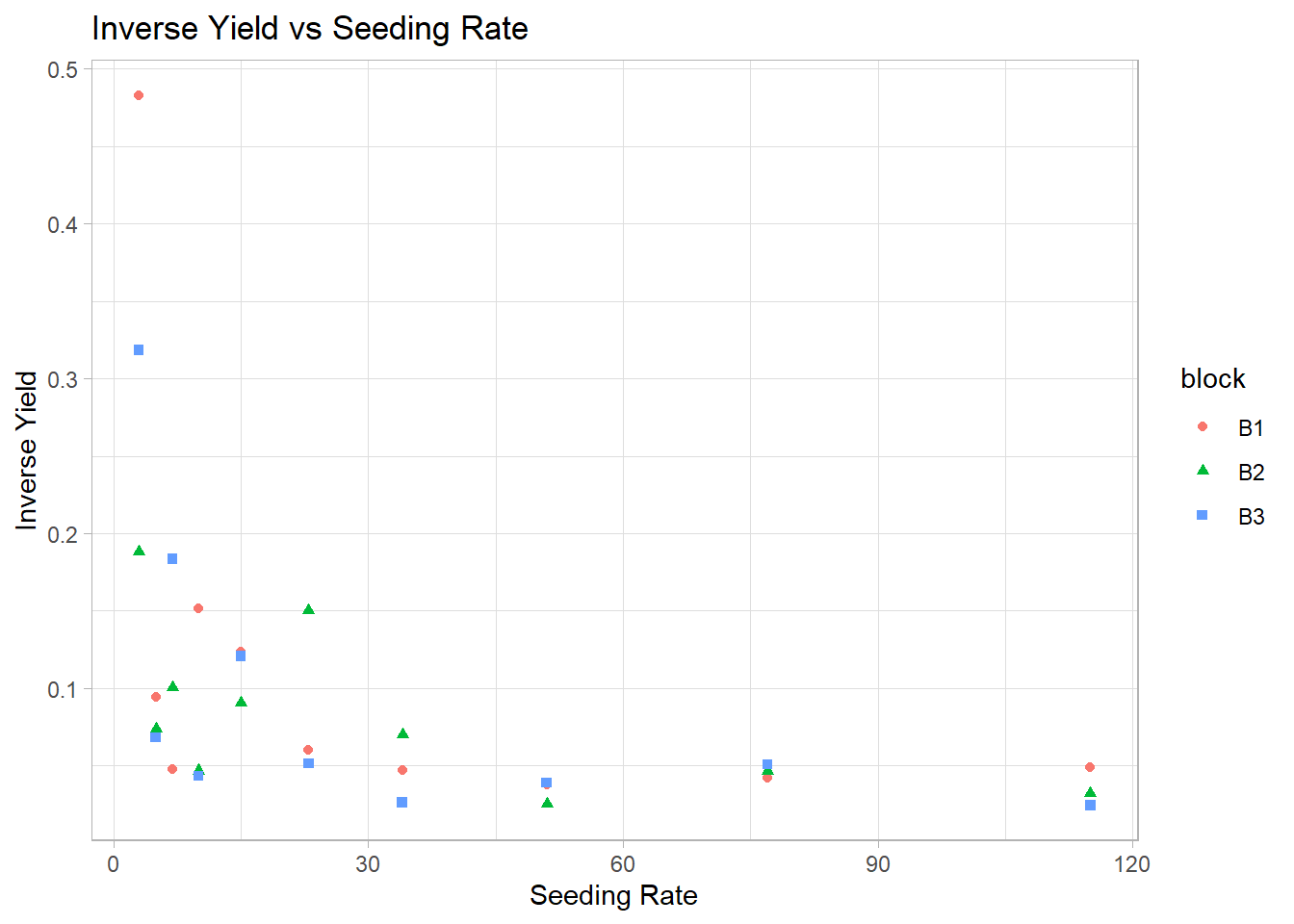
Figure 7.11: Inverse Yield vs Seeding Rate
3. Fit Gamma Regression Model
Gamma regression models yield as a function of seeding rate using an inverse link:
\[ \eta_{ij} = \beta_{0j} + \beta_{1j} x_{ij} + \beta_2 x_{ij}^2, \quad Y_{ij} = \eta_{ij}^{-1} \]
m1 <- glm(y ~ block + block * x + block * I(x^2),
data = gammaDat, family = Gamma(link = "inverse"))
summary(m1)
#>
#> Call:
#> glm(formula = y ~ block + block * x + block * I(x^2), family = Gamma(link = "inverse"),
#> data = gammaDat)
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 1.115e-01 2.870e-02 3.886 0.000854 ***
#> blockB2 -1.208e-02 3.880e-02 -0.311 0.758630
#> blockB3 -2.386e-02 3.683e-02 -0.648 0.524029
#> x -2.075e-03 1.099e-03 -1.888 0.072884 .
#> I(x^2) 1.372e-05 9.109e-06 1.506 0.146849
#> blockB2:x 5.198e-04 1.468e-03 0.354 0.726814
#> blockB3:x 7.475e-04 1.393e-03 0.537 0.597103
#> blockB2:I(x^2) -5.076e-06 1.184e-05 -0.429 0.672475
#> blockB3:I(x^2) -6.651e-06 1.123e-05 -0.592 0.560012
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> (Dispersion parameter for Gamma family taken to be 0.3232083)
#>
#> Null deviance: 13.1677 on 29 degrees of freedom
#> Residual deviance: 7.8605 on 21 degrees of freedom
#> AIC: 225.32
#>
#> Number of Fisher Scoring iterations: 54. Predictions and Visualization
# Generate new data for prediction
newdf <-
expand.grid(x = seq(0, 120, length = 50),
block = factor(c("B1", "B2", "B3")))
# Predict responses
newdf$pred <- predict(m1, newdata = newdf, type = "response")# Plot predictions
ggplot(gammaDat, aes(x = x, y = y)) +
geom_point(aes(color = block, shape = block)) +
geom_line(data = newdf, aes(
x = x,
y = pred,
color = block,
linetype = block
)) +
labs(title = "Predicted Yield by Seeding Rate",
x = "Seeding Rate",
y = "Yield")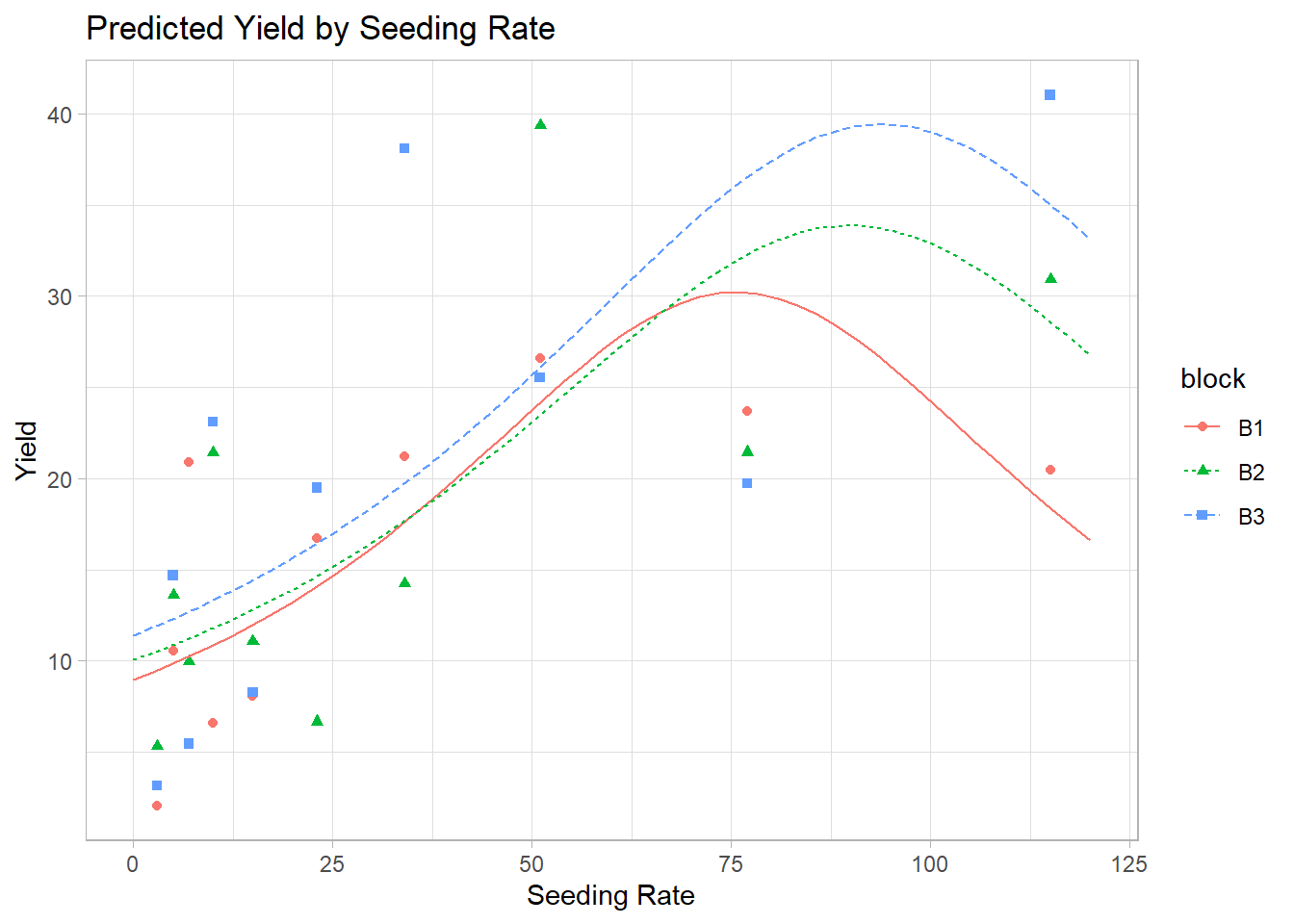
Figure 7.12: Predicted Yield by Seeding Rate