34 Instrumental Variables
In many empirical settings, we seek to estimate the causal effect of an explanatory variable \(X\) on an outcome variable \(Y\). A common starting point is the Ordinary Least Squares regression:
\[ Y = \beta_0 + \beta_1 X + \varepsilon. \]
For OLS to provide an unbiased and consistent estimate of \(\beta_1\), the explanatory variable \(X\) must satisfy the exogeneity condition:
\[ \mathbb{E}[\varepsilon \mid X] = 0. \]
However, when \(X\) is correlated with the error term \(\varepsilon\), this assumption is violated, leading to endogeneity. As a result, the OLS estimator is biased and inconsistent. Common causes of endogeneity include:
- Omitted Variable Bias (OVB): When a relevant variable is omitted from the regression, leading to correlation between \(X\) and \(\varepsilon\).
- Simultaneity: When \(X\) and \(Y\) are jointly determined, such as in supply-and-demand models.
- Measurement Error: Errors in measuring \(X\) introduce bias in estimation.
- Attenuation Bias in Errors-in-Variables: measurement error in the independent variable leads to an underestimate of the true effect (biasing the coefficient toward zero).
Instrumental Variables (IV) estimation addresses endogeneity by introducing an instrument \(Z\) that affects \(Y\) only through \(X\). Similar to RCT, we try to introduce randomization (random assignment to treatment) to our treatment variable by using only variation in the instrument.
Logic of using an instrument:
Use only exogenous variation to see the variation in treatment (try to exclude all endogenous variation in the treatment)
Use only exogenous variation to see the variation in outcome (try to exclude all endogenous variation in the outcome)
See the relationship between treatment and outcome in terms of residual variations that are exogenous to omitted variables.
For an instrument \(Z\) to be valid, it must satisfy two conditions:
Relevance Condition: The instrument \(Z\) must be correlated with the endogenous variable \(X\): \[ \text{Cov}(Z, X) \neq 0. \]
Exogeneity Condition (Exclusion Restriction): The instrument \(Z\) must be uncorrelated with the error term \(\varepsilon\) and affect \(Y\) only through \(X\): \[ \text{Cov}(Z, \varepsilon) = 0. \]
These conditions ensure that \(Z\) provides exogenous variation in \(X\), allowing us to isolate the causal effect of \(X\) on \(Y\).
These conditions ensure that \(Z\) provides exogenous variation in \(X\), allowing us to estimate the causal effect of \(X\) on \(Y\). Random assignment of \(Z\) helps ensure exogeneity, but we must also confirm that \(Z\) influences \(Y\) only through \(X\) to satisfy the exclusion restriction.
The IV approach dates back to early econometric research in the 1920s and 1930s, with a significant role in Cowles Commission studies on simultaneous equations. Key contributions include:
- P. G. Wright (1928): One of the earliest applications, studying supply and demand for pig iron.
- J. Angrist and Imbens (1991): Popularized IV methods using quarter-of-birth as an instrument for education.
The credibility revolution in econometrics (1990s–2000s) led to widespread use of IVs in applied research, particularly in economics, political science, and epidemiology.
34.1 Challenges with Instrumental Variables
While IVs can provide a solution to endogeneity, several challenges arise:
- Exclusion Restriction Violations: If \(Z\) affects \(Y\) through any channel other than \(X\), the IV estimate is biased.
- Repeated Use of Instruments: Common instruments, such as weather or policy changes, may be invalid due to their widespread application across studies (Gallen 2020). One needs to test for invalid instruments (Hausman-like test).
- A notable example is Mellon (2021), who documents that 289 social sciences studies have used weather as an instrument for 195 variables, raising concerns about exclusion violations.
- Heterogeneous Treatment Effects: The Local Average Treatment Effect (LATE) estimated by IV applies only to compliers—units whose treatment status is affected by the instrument.
- Weak Instruments: Too little correlation with the endogenous regressor yields unstable estimates.
- Invalid Instruments: If the instrument violates exogeneity, your results are inconsistent.
- Interpretation Mistakes: The IV identifies only the effect for those “marginal” units whose treatment status is driven by the instrument.
34.2 Framework for Instrumental Variables
We consider a binary treatment framework where:
\(D_i \sim Bernoulli(p)\) is a dummy treatment variable.
\((Y_{0i}, Y_{1i})\) are the potential outcomes under control and treatment.
The observed outcome is: \[ Y_i = Y_{0i} + (Y_{1i} - Y_{0i}) D_i. \]
-
We introduce an instrumental variable \(Z_i\) satisfying: \[ Z_i \perp (Y_{0i}, Y_{1i}, D_{0i}, D_{1i}). \]
- This means \(Z_i\) is independent of potential outcomes and potential treatment status.
- \(Z_i\) must also be correlated with \(D_i\) to satisfy the relevance condition.
34.2.1 Constant-Treatment-Effect Model
Under the constant treatment effect assumption (i.e., the treatment effect is the same for all individuals),
\[ \begin{aligned} Y_{0i} &= \alpha + \eta_i, \\ Y_{1i} - Y_{0i} &= \rho, \\ Y_i &= Y_{0i} + D_i (Y_{1i} - Y_{0i}) \\ &= \alpha + \eta_i + D_i \rho \\ &= \alpha + \rho D_i + \eta_i. \end{aligned} \]
where:
- \(\eta_i\) captures individual-level heterogeneity.
- \(\rho\) is the constant treatment effect.
The problem with OLS estimation is that \(D_i\) may be correlated with \(\eta_i\), leading to endogeneity bias.
34.2.2 Instrumental Variable Solution
A valid instrument \(Z_i\) allows us to estimate the causal effect \(\rho\) via:
\[ \begin{aligned} \rho &= \frac{\text{Cov}(Y_i, Z_i)}{\text{Cov}(D_i, Z_i)} \\ &= \frac{\text{Cov}(Y_i, Z_i) / V(Z_i) }{\text{Cov}(D_i, Z_i) / V(Z_i)} \\ &= \frac{\text{Reduced form estimate}}{\text{First-stage estimate}} \\ &= \frac{E[Y_i |Z_i = 1] - E[Y_i | Z_i = 0]}{E[D_i |Z_i = 1] - E[D_i | Z_i = 0 ]}. \end{aligned} \]
This ratio measures the treatment effect only if \(Z_i\) is a valid instrument.
34.2.3 Heterogeneous Treatment Effects and the LATE Framework
In a more general framework where treatment effects vary across individuals,
Define potential outcomes as: \[ Y_i(d,z) = \text{outcome for unit } i \text{ given } D_i = d, Z_i = z. \]
-
Define treatment status based on \(Z_i\): \[ D_i = D_{0i} + Z_i (D_{1i} - D_{0i}). \]
where:
- \(D_{1i}\) is the treatment status when \(Z_i = 1\).
- \(D_{0i}\) is the treatment status when \(Z_i = 0\).
- \(D_{1i} - D_{0i}\) is the causal effect of \(Z_i\) on \(D_i\).
34.2.4 Assumptions for LATE Identification
34.2.4.1 Independence (Instrument Randomization)
The instrument must be as good as randomly assigned:
\[ [\{Y_i(d,z); \forall d, z \}, D_{1i}, D_{0i} ] \perp Z_i. \]
This ensures that \(Z_i\) is uncorrelated with potential outcomes and potential treatment status.
This assumption let the first-stage equation be the average causal effect of \(Z_i\) on \(D_i\)
\[ \begin{aligned} E[D_i |Z_i = 1] - E[D_i | Z_i = 0] &= E[D_{1i} |Z_i = 1] - E[D_{0i} |Z_i = 0] \\ &= E[D_{1i} - D_{0i}] \end{aligned} \]
This assumption also is sufficient for a causal interpretation of the reduced form, where we see the effect of the instrument \(Z_i\) on the outcome \(Y_i\):
\[ E[Y_i |Z_i = 1 ] - E[Y_i|Z_i = 0] = E[Y_i (D_{1i}, Z_i = 1) - Y_i (D_{0i} , Z_i = 0)] \]
34.2.4.2 Exclusion Restriction
This is also known as the existence of the instrument assumption (G. W. Imbens and Angrist 1994). The instrument should only affect \(Y_i\) through \(D_i\) (i.e., the treatment \(D_i\) fully mediates the effect of \(Z_i\) on \(Y_i\)):
\[ \begin{aligned} Y_{1i} &= Y_i (1,1) = Y_i (1,0)\\ Y_{0i} &= Y_i (0,1) = Y_i (0,0) \end{aligned} \]
Under this assumption (and assume \(Y_{1i, Y_{0i}}\) already satisfy the independence assumption), the observed outcome \(Y_i\) can be rewritten as:
\[ \begin{aligned} Y_i &= Y_i (0, Z_i) + [Y_i (1 , Z_i) - Y_i (0, Z_i)] D_i \\ &= Y_{0i} + (Y_{1i} - Y_{0i}) D_i. \end{aligned} \]
This assumption let us go from reduced-form causal effects to treatment effects (J. D. Angrist and Imbens 1995).
34.2.4.3 Monotonicity (No Defiers)
We assume that \(Z_i\) affects \(D_i\) in a monotonic way:
\[ D_{1i} \geq D_{0i}, \quad \forall i. \]
- This assumption lets us assume that there is a first stage, in which we examine the proportion of the population that \(D_i\) is driven by \(Z_i\). It implies that \(Z_i\) only moves individuals toward treatment, but never away. This rules out “defiers” (i.e., individuals who would have taken the treatment when not assigned but refuse when assigned).
- This assumption is used to solve to problem of the shifts between participation status back to non-participation status.
Alternatively, one can solve the same problem by assuming constant (homogeneous) treatment effect (G. W. Imbens and Angrist 1994), but this is rather restrictive.
A third solution is the assumption that there exists a value of the instrument, where the probability of participation conditional on that value is 0 J. Angrist and Imbens (1991).
Under monotonicity,
\[ \begin{aligned} E[D_{1i} - D_{0i} ] = P[D_{1i} > D_{0i}]. \end{aligned} \]
34.2.5 Local Average Treatment Effect Theorem
Given Independence, Exclusion, and Monotonicity, we obtain the LATE result (J. D. Angrist and Pischke 2009, 4.4.1):
\[ \begin{aligned} \frac{E[Y_i | Z_i = 1] - E[Y_i | Z_i = 0]}{E[D_i |Z_i = 1] - E[D_i |Z_i = 0]} = E[Y_{1i} - Y_{0i} | D_{1i} > D_{0i}]. \end{aligned} \]
This states that the IV estimator recovers the causal effect only for compliers—units whose treatment status changes due to \(Z_i\).
IV only identifies treatment effects for switchers (compliers):
| Switcher Type | Compliance Type | Definition |
|---|---|---|
| Switchers | Compliers | \(D_{1i} > D_{0i}\) (take treatment if \(Z_i = 1\), not if \(Z_i = 0\)) |
| Non-switchers | Always-Takers | \(D_{1i} = D_{0i} = 1\) (always take treatment) |
| Non-switchers | Never-Takers | \(D_{1i} = D_{0i} = 0\) (never take treatment) |
- IV estimates nothing for always-takers and never-takers since their treatment status is unaffected by \(Z_i\) (Similar to the fixed-effects models).
34.2.6 IV in Randomized Trials (Noncompliance)
- In randomized trials, if compliance is imperfect (i.e., compliance is voluntary), where individuals in the treatment group will not always take the treatment (e.g., selection bias), intention-to-treat (ITT) estimates are valid but contaminated by noncompliance.
- IV estimation using random assignment (\(Z_i\)) as an instrument for actual treatment received (\(D_i\)) recovers the LATE.
\[ \begin{aligned} \frac{E[Y_i |Z_i = 1] - E[Y_i |Z_i = 0]}{E[D_i |Z_i = 1]} = \frac{\text{Intent-to-Treat Effect}}{\text{Compliance Rate}} = E[Y_{1i} - Y_{0i} |D_i = 1]. \end{aligned} \]
Under full compliance, LATE = Treatment Effect on the Treated (TOT).
34.3 Estimation
34.3.1 Two-Stage Least Squares Estimation
Two-Stage Least Squares (2SLS) is the most widely used IV estimator It’s a special case of IV-GMM. Consider the structural equation:
\[ Y_i = X_i \beta + \varepsilon_i, \]
where \(X_i\) is endogenous. We introduce an instrument \(Z_i\) satisfying:
- Relevance: \(Z_i\) is correlated with \(X_i\).
- Exogeneity: \(Z_i\) is uncorrelated with \(\varepsilon_i\).
2SLS Steps
-
First-Stage Regression: Predict \(X_i\) using the instrument: \[ X_i = \pi_0 + \pi_1 Z_i + v_i. \]
- Obtain fitted values \(\hat{X}_i = \pi_0 + \pi_1 Z_i\).
-
Second-Stage Regression: Use \(\hat{X}_i\) in place of \(X_i\): \[ Y_i = \beta_0 + \beta_1 \hat{X}_i + \varepsilon_i. \]
- The estimated \(\hat{\beta}_1\) is our IV estimator.
library(fixest)
base = iris
names(base) = c("y", "x1", "x_endo_1", "x_inst_1", "fe")
set.seed(2)
base$x_inst_2 = 0.2 * base$y + 0.2 * base$x_endo_1 + rnorm(150, sd = 0.5)
base$x_endo_2 = 0.2 * base$y - 0.2 * base$x_inst_1 + rnorm(150, sd = 0.5)
# IV Estimation
est_iv = feols(y ~ x1 | x_endo_1 + x_endo_2 ~ x_inst_1 + x_inst_2, base)
summary(est_iv)
#> TSLS estimation - Dep. Var.: y
#> Endo. : x_endo_1, x_endo_2
#> Instr. : x_inst_1, x_inst_2
#> Second stage: Dep. Var.: y
#> Observations: 150
#> Standard-errors: IID
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 1.831380 0.411435 4.45121 1.6844e-05 ***
#> fit_x_endo_1 0.444982 0.022086 20.14744 < 2.2e-16 ***
#> fit_x_endo_2 0.639916 0.307376 2.08186 3.9100e-02 *
#> x1 0.565095 0.084715 6.67051 4.9180e-10 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> RMSE: 0.398842 Adj. R2: 0.725033
#> F-test (1st stage), x_endo_1: stat = 903.1628, p < 2.2e-16 , on 2 and 146 DoF.
#> F-test (1st stage), x_endo_2: stat = 3.2583, p = 0.041268, on 2 and 146 DoF.
#> Wu-Hausman: stat = 6.7918, p = 0.001518, on 2 and 144 DoF.Diagnostic Tests
To assess instrument validity:
fitstat(est_iv, type = c("n", "f", "ivf", "ivf1", "ivf2", "ivwald", "cd"))
#> Observations: 150
#> F-test: stat = 131.9612, p < 2.2e-16 , on 3 and 146 DoF.
#> F-test (1st stage), x_endo_1: stat = 903.1628, p < 2.2e-16 , on 2 and 146 DoF.
#> F-test (1st stage), x_endo_2: stat = 3.2583, p = 0.041268, on 2 and 146 DoF.
#> F-test (2nd stage): stat = 194.1967, p < 2.2e-16 , on 2 and 146 DoF.
#> Wald (1st stage), x_endo_1 : stat = 903.1628, p < 2.2e-16 , on 2 and 146 DoF, VCOV: IID.
#> Wald (1st stage), x_endo_2 : stat = 3.2583, p = 0.041268, on 2 and 146 DoF, VCOV: IID.
#> Cragg-Donald: 3.11162To set default printing
# always add second-stage Wald test
setFixest_print(fitstat = ~ . + ivwald2)
est_ivTo see results from different stages
# first-stage
summary(est_iv, stage = 1)
# second-stage
summary(est_iv, stage = 2)
# both stages
etable(summary(est_iv, stage = 1:2), fitstat = ~ . + ivfall + ivwaldall.p)
etable(summary(est_iv, stage = 2:1), fitstat = ~ . + ivfall + ivwaldall.p)
# .p means p-value, not statistic
# `all` means IV only34.3.2 IV-GMM
The Generalized Method of Moments (GMM) provides a flexible estimation framework that generalizes the Instrumental Variables (IV) approach, including 2SLS as a special case. The key idea behind GMM is to use moment conditions derived from economic models to estimate parameters efficiently, even in the presence of endogeneity.
Consider the standard linear regression model:
\[ Y = X\beta + u, \quad u \sim (0, \Omega) \]
where:
- \(Y\) is an \(N \times 1\) vector of the dependent variable.
- \(X\) is an \(N \times k\) matrix of endogenous regressors.
- \(\beta\) is a \(k \times 1\) vector of coefficients.
- \(u\) is an \(N \times 1\) vector of error terms.
- \(\Omega\) is the variance-covariance matrix of \(u\).
To address endogeneity in \(X\), we introduce an \(N \times l\) matrix of instruments, \(Z\), where \(l \geq k\). The moment conditions are then given by:
\[ E[Z_i' u_i] = E[Z_i' (Y_i - X_i \beta)] = 0. \]
In practice, these expectations are replaced by their sample analogs. The empirical moment conditions are given by:
\[ \bar{g}(\beta) = \frac{1}{N} \sum_{i=1}^{N} Z_i' (Y_i - X_i \beta) = \frac{1}{N} Z' (Y - X\beta). \]
GMM estimates \(\beta\) by minimizing a quadratic function of these sample moments.
34.3.2.1 IV and GMM Estimators
- Exactly Identified Case (\(l = k\))
When the number of instruments equals the number of endogenous regressors (\(l = k\)), the moment conditions uniquely determine \(\beta\). In this case, the IV estimator is:
\[ \hat{\beta}_{IV} = (Z'X)^{-1}Z'Y. \]
This is equivalent to the classical 2SLS estimator.
- Overidentified Case (\(l > k\))
When there are more instruments than endogenous variables (\(l > k\)), the system has more moment conditions than parameters. In this case, we project \(X\) onto the instrument space:
\[ \hat{X} = Z(Z'Z)^{-1} Z' X = P_Z X. \]
The 2SLS estimator is then given by:
\[ \begin{aligned} \hat{\beta}_{2SLS} &= (\hat{X}'X)^{-1} \hat{X}' Y \\ &= (X'P_Z X)^{-1} X' P_Z Y. \end{aligned} \]
However, 2SLS does not optimally weight the instruments when \(l > k\). The IV-GMM approach resolves this issue.
34.3.2.2 IV-GMM Estimation
The GMM estimator is obtained by minimizing the objective function:
\[ J (\hat{\beta}_{GMM} ) = N \bar{g}(\hat{\beta}_{GMM})' W \bar{g} (\hat{\beta}_{GMM}), \]
where \(W\) is an \(l \times l\) symmetric weighting matrix.
For the IV-GMM estimator, solving the first-order conditions yields:
\[ \hat{\beta}_{GMM} = (X'ZWZ' X)^{-1} X'ZWZ'Y. \]
For any weighting matrix \(W\), this is a consistent estimator. The optimal choice of \(W\) is \(S^{-1}\), where \(S\) is the covariance matrix of the moment conditions:
\[ S = E[Z' u u' Z] = \lim_{N \to \infty} N^{-1} [Z' \Omega Z]. \]
A feasible estimator replaces \(S\) with its sample estimate from the 2SLS residuals:
\[ \hat{\beta}_{FEGMM} = (X'Z \hat{S}^{-1} Z' X)^{-1} X'Z \hat{S}^{-1} Z'Y. \]
When \(\Omega\) satisfies standard assumptions:
- Errors are independently and identically distributed.
- \(S = \sigma_u^2 I_N\).
- The optimal weighting matrix is proportional to the identity matrix.
Then, the IV-GMM estimator simplifies to the standard IV (or 2SLS) estimator.
Comparison of 2SLS and IV-GMM
| Feature | 2SLS | IV-GMM |
|---|---|---|
| Instrument usage | Uses a subset of available instruments | Uses all available instruments |
| Weighting | No weighting applied | Weights instruments for efficiency |
| Efficiency | Suboptimal in overidentified cases | Efficient when \(W = S^{-1}\) |
| Overidentification test | Not available | Uses Hansen’s \(J\)-test (overid test) |
Key Takeaways:
- Use IV-GMM whenever overidentification is a concern (i.e., \(l > k\)).
- 2SLS is a special case of IV-GMM when the weighting matrix is proportional to the identity matrix.
- IV-GMM improves efficiency by optimally weighting the moment conditions.
# Standard approach
library(gmm)
gmm_model <- gmm(y ~ x1, ~ x_inst_1 + x_inst_2, data = base)
summary(gmm_model)
#>
#> Call:
#> gmm(g = y ~ x1, x = ~x_inst_1 + x_inst_2, data = base)
#>
#>
#> Method: twoStep
#>
#> Kernel: Quadratic Spectral(with bw = 0.72368 )
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 1.4385e+01 1.8960e+00 7.5871e+00 3.2715e-14
#> x1 -2.7506e+00 6.2101e-01 -4.4292e+00 9.4584e-06
#>
#> J-Test: degrees of freedom is 1
#> J-test P-value
#> Test E(g)=0: 7.9455329 0.0048206
#>
#> Initial values of the coefficients
#> (Intercept) x1
#> 16.117875 -3.36062234.3.2.3 Overidentification Test: Hansen’s \(J\)-Statistic
A key advantage of IV-GMM is that it allows testing of instrument validity through the Hansen \(J\)-test (also known as the GMM distance test or Hayashi’s C-statistic). The test statistic is:
\[ J = N \bar{g}(\hat{\beta}_{GMM})' \hat{S}^{-1} \bar{g} (\hat{\beta}_{GMM}), \]
which follows a \(\chi^2\) distribution with degrees of freedom equal to the number of overidentifying restrictions (\(l - k\)). A significant \(J\)-statistic suggests that the instruments may not be valid.
34.3.2.4 Cluster-Robust Standard Errors
In empirical applications, errors often exhibit heteroskedasticity or intra-group correlation (clustering), violating the assumption of independently and identically distributed errors. Standard IV-GMM estimators remain consistent but may not be efficient if clustering is ignored.
To address this, we adjust the GMM weighting matrix by incorporating cluster-robust variance estimation. Specifically, the covariance matrix of the moment conditions \(S\) is estimated as:
\[ \hat{S} = \frac{1}{N} \sum_{c=1}^{C} \left( \sum_{i \in c} Z_i' u_i \right) \left( \sum_{i \in c} Z_i' u_i \right)', \]
where:
\(C\) is the number of clusters,
\(i \in c\) represents observations belonging to cluster \(c\),
\(u_i\) is the residual for observation \(i\),
\(Z_i\) is the vector of instruments.
Using this robust weighting matrix, we compute a clustered GMM estimator that remains consistent and improves inference when clustering is present.
# Load required packages
library(gmm)
library(dplyr)
library(MASS) # For generalized inverse if needed
# General IV-GMM function with clustering
gmmcl <- function(formula, instruments, data, cluster_var, lambda = 1e-6) {
# Ensure cluster_var exists in data
if (!(cluster_var %in% colnames(data))) {
stop("Error: Cluster variable not found in data.")
}
# Step 1: Initial GMM estimation (identity weighting matrix)
initial_gmm <- gmm(formula, instruments, data = data, vcov = "TrueFixed",
weightsMatrix = diag(ncol(model.matrix(instruments, data))))
# Extract residuals
u_hat <- residuals(initial_gmm)
# Matrix of instruments
Z <- model.matrix(instruments, data)
# Ensure clusters are treated as a factor
data[[cluster_var]] <- as.factor(data[[cluster_var]])
# Compute clustered weighting matrix
cluster_groups <- split(seq_along(u_hat), data[[cluster_var]])
# Remove empty clusters (if any)
cluster_groups <- cluster_groups[lengths(cluster_groups) > 0]
# Initialize cluster-based covariance matrix
S_cluster <- matrix(0, ncol(Z), ncol(Z)) # Zero matrix
# Compute clustered weight matrix
for (indices in cluster_groups) {
if (length(indices) > 0) { # Ensure valid clusters
u_cluster <- matrix(u_hat[indices], ncol = 1) # Convert to column matrix
Z_cluster <- Z[indices, , drop = FALSE] # Keep matrix form
S_cluster <- S_cluster + t(Z_cluster) %*% (u_cluster %*% t(u_cluster)) %*% Z_cluster
}
}
# Normalize by sample size
S_cluster <- S_cluster / nrow(data)
# Ensure S_cluster is invertible
S_cluster <- S_cluster + lambda * diag(ncol(S_cluster)) # Regularization
# Compute inverse or generalized inverse if needed
if (qr(S_cluster)$rank < ncol(S_cluster)) {
S_cluster_inv <- ginv(S_cluster) # Use generalized inverse (MASS package)
} else {
S_cluster_inv <- solve(S_cluster)
}
# Step 2: GMM estimation using clustered weighting matrix
final_gmm <- gmm(formula, instruments, data = data, vcov = "TrueFixed",
weightsMatrix = S_cluster_inv)
return(final_gmm)
}
# Example: Simulated Data for IV-GMM with Clustering
set.seed(123)
n <- 200 # Total observations
C <- 50 # Number of clusters
data <- data.frame(
cluster = rep(1:C, each = n / C), # Cluster variable
z1 = rnorm(n),
z2 = rnorm(n),
x1 = rnorm(n),
y1 = rnorm(n)
)
data$x1 <- data$z1 + data$z2 + rnorm(n) # Endogenous regressor
data$y1 <- data$x1 + rnorm(n) # Outcome variable
# Run standard IV-GMM (without clustering)
gmm_results_standard <- gmm(y1 ~ x1, ~ z1 + z2, data = data)
# Run IV-GMM with clustering
gmm_results_clustered <- gmmcl(y1 ~ x1, ~ z1 + z2, data = data, cluster_var = "cluster")
# Display results for comparison
summary(gmm_results_standard)
#>
#> Call:
#> gmm(g = y1 ~ x1, x = ~z1 + z2, data = data)
#>
#>
#> Method: twoStep
#>
#> Kernel: Quadratic Spectral(with bw = 1.09893 )
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 4.4919e-02 6.5870e-02 6.8193e-01 4.9528e-01
#> x1 9.8409e-01 4.4215e-02 2.2257e+01 9.6467e-110
#>
#> J-Test: degrees of freedom is 1
#> J-test P-value
#> Test E(g)=0: 1.6171 0.2035
#>
#> Initial values of the coefficients
#> (Intercept) x1
#> 0.05138658 0.98580796
summary(gmm_results_clustered)
#>
#> Call:
#> gmm(g = formula, x = instruments, vcov = "TrueFixed", weightsMatrix = S_cluster_inv,
#> data = data)
#>
#>
#> Method: One step GMM with fixed W
#>
#> Kernel: Quadratic Spectral
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 4.9082e-02 7.0878e-05 6.9249e+02 0.0000e+00
#> x1 9.8238e-01 5.2798e-05 1.8606e+04 0.0000e+00
#>
#> J-Test: degrees of freedom is 1
#> J-test P-value
#> Test E(g)=0: 1247099 034.3.3 Limited Information Maximum Likelihood
LIML is an alternative to 2SLS that performs better when instruments are weak.
It solves: \[ \min_{\lambda} \left| \begin{bmatrix} Y - X\beta \\ \lambda (D - X\gamma) \end{bmatrix} \right| \] where \(\lambda\) is an eigenvalue.
34.3.4 Jackknife IV
JIVE reduces small-sample bias by leaving each observation out when estimating first-stage fitted values:
\[ \begin{aligned} \hat{X}_i^{(-i)} &= Z_i (Z_{-i}'Z_{-i})^{-1} Z_{-i}'X_{-i}. \\ \hat{\beta}_{JIVE} &= (X^{(-i)'}X^{(-i)})^{-1}X^{(-i)'} Y \end{aligned} \]
library(AER)
jive_model = ivreg(y ~ x_endo_1 | x_inst_1, data = base, method = "jive")
summary(jive_model)
#>
#> Call:
#> ivreg(formula = y ~ x_endo_1 | x_inst_1, data = base, method = "jive")
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -1.2390 -0.3022 -0.0206 0.2772 1.0039
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 4.34586 0.08096 53.68 <2e-16 ***
#> x_endo_1 0.39848 0.01964 20.29 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.4075 on 148 degrees of freedom
#> Multiple R-Squared: 0.7595, Adjusted R-squared: 0.7578
#> Wald test: 411.6 on 1 and 148 DF, p-value: < 2.2e-1634.3.5 Control Function Approach
The Control Function (CF) approach, also known as two-stage residual inclusion (2SRI), is a method used to address endogeneity in regression models. This approach is particularly suited for models with nonadditive errors, such as discrete choice models or cases where both the endogenous variable and the outcome are binary.
The control function approach is particularly useful in:
- Binary outcome and binary endogenous variable models:
- In rare events, the second stage typically uses a logistic model (E. Tchetgen Tchetgen 2014).
- In non-rare events, a risk ratio regression is often more appropriate.
- Marketing applications:
- Used in consumer choice models to account for endogeneity in demand estimation (Petrin and Train 2010).
The general model setup is:
\[ Y = g(X) + U \]
\[ X = \pi(Z) + V \]
with the key assumptions:
Conditional mean independence:
\[E(U |Z,V) = E(U|V)\]
This implies that once we control for \(V\), the instrumental variable \(Z\) does not directly affect \(U\).Instrument relevance:
\[E(V|Z) = 0\]
This ensures that \(Z\) is a valid instrument for \(X\).
Under the control function approach, the expectation of \(Y\) conditional on \((Z,V)\) can be rewritten as:
\[ E(Y|Z,V) = g(X) + E(U|Z,V) = g(X) + E(U|V) = g(X) + h(V). \]
Here, \(h(V)\) is the control function that captures endogeneity through the first-stage residuals.
34.3.5.1 Implementation
Rather than replacing the endogenous variable \(X_i\) with its predicted value \(\hat{X}_i\), the CF approach explicitly incorporates the residuals from the first-stage regression:
Stage 1: Estimate First-Stage Residuals
Estimate the endogenous variable using its instrumental variables:
\[ X_i = Z_i \pi + v_i. \]
Obtain the residuals:
\[ \hat{v}_i = X_i - Z_i \hat{\pi}. \]
Stage 2: Include Residuals in Outcome Equation
Regress the outcome variable on \(X_i\) and the first-stage residuals:
\[ Y_i = X_i \beta + \gamma \hat{v}_i + \varepsilon_i. \]
If endogeneity is present, \(\gamma \neq 0\); otherwise, the endogenous regressor \(X\) would be exogenous.
34.3.5.2 Comparison to Two-Stage Least Squares
The control function method differs from 2SLS depending on whether the model is linear or nonlinear:
- Linear Endogenous Variables:
- When both \(X\) and \(Y\) are continuous, the CF approach is equivalent to 2SLS.
- Nonlinear Endogenous Variables:
- If \(X\) is nonlinear (e.g., a binary treatment), CF differs from 2SLS and often performs better.
- Nonlinear in Parameters:
- In models where \(g(X)\) is nonlinear (e.g., logit/probit models), CF is typically superior to 2SLS because it explicitly models endogeneity via the control function \(h(V)\).
library(fixest)
library(tidyverse)
library(modelsummary)
# Set the seed for reproducibility
set.seed(123)
n = 1000
# Generate the exogenous variable from a normal distribution
exogenous <- rnorm(n, mean = 5, sd = 1)
# Generate the omitted variable as a function of the exogenous variable
omitted <- rnorm(n, mean = 2, sd = 1)
# Generate the endogenous variable as a function of the omitted variable and the exogenous variable
endogenous <- 5 * omitted + 2 * exogenous + rnorm(n, mean = 0, sd = 1)
# nonlinear endogenous variable
endogenous_nonlinear <- 5 * omitted^2 + 2 * exogenous + rnorm(100, mean = 0, sd = 1)
unrelated <- rexp(n, rate = 1)
# Generate the response variable as a function of the endogenous variable and the omitted variable
response <- 4 + 3 * endogenous + 6 * omitted + rnorm(n, mean = 0, sd = 1)
response_nonlinear <- 4 + 3 * endogenous_nonlinear + 6 * omitted + rnorm(n, mean = 0, sd = 1)
response_nonlinear_para <- 4 + 3 * endogenous ^ 2 + 6 * omitted + rnorm(n, mean = 0, sd = 1)
# Combine the variables into a data frame
my_data <-
data.frame(
exogenous,
omitted,
endogenous,
response,
unrelated,
response,
response_nonlinear,
response_nonlinear_para
)
# View the first few rows of the data frame
# head(my_data)
wo_omitted <- feols(response ~ endogenous + sw0(unrelated), data = my_data)
w_omitted <- feols(response ~ endogenous + omitted + unrelated, data = my_data)
# ivreg::ivreg(response ~ endogenous + unrelated | exogenous, data = my_data)
iv <- feols(response ~ 1 + sw0(unrelated) | endogenous ~ exogenous, data = my_data)
etable(
wo_omitted,
w_omitted,
iv,
digits = 2
# vcov = list("each", "iid", "hetero")
)
#> wo_omitted.1 wo_omitted.2 w_omitted iv.1
#> Dependent Var.: response response response response
#>
#> Constant -3.8*** (0.30) -3.6*** (0.31) 3.9*** (0.16) 12.0*** (1.4)
#> endogenous 4.0*** (0.01) 4.0*** (0.01) 3.0*** (0.01) 3.2*** (0.07)
#> unrelated -0.14. (0.08) -0.02 (0.03)
#> omitted 6.0*** (0.08)
#> _______________ ______________ ______________ _____________ _____________
#> S.E. type IID IID IID IID
#> Observations 1,000 1,000 1,000 1,000
#> R2 0.98756 0.98760 0.99817 0.11406
#> Adj. R2 0.98755 0.98757 0.99816 0.11317
#>
#> iv.2
#> Dependent Var.: response
#>
#> Constant 12.2*** (1.4)
#> endogenous 3.2*** (0.07)
#> unrelated -0.28. (0.16)
#> omitted
#> _______________ _____________
#> S.E. type IID
#> Observations 1,000
#> R2 0.11608
#> Adj. R2 0.11430
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Linear in parameter and linear in endogenous variable
# manual
# 2SLS
first_stage = lm(endogenous ~ exogenous, data = my_data)
new_data = cbind(my_data, new_endogenous = predict(first_stage, my_data))
second_stage = lm(response ~ new_endogenous, data = new_data)
summary(second_stage)
#>
#> Call:
#> lm(formula = response ~ new_endogenous, data = new_data)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -68.126 -14.949 0.608 15.099 73.842
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 11.9910 5.7671 2.079 0.0379 *
#> new_endogenous 3.2097 0.2832 11.335 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 21.49 on 998 degrees of freedom
#> Multiple R-squared: 0.1141, Adjusted R-squared: 0.1132
#> F-statistic: 128.5 on 1 and 998 DF, p-value: < 2.2e-16
new_data_cf = cbind(my_data, residual = resid(first_stage))
second_stage_cf = lm(response ~ endogenous + residual, data = new_data_cf)
summary(second_stage_cf)
#>
#> Call:
#> lm(formula = response ~ endogenous + residual, data = new_data_cf)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -5.1039 -1.0065 0.0247 0.9480 4.2521
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 11.99102 0.39849 30.09 <2e-16 ***
#> endogenous 3.20974 0.01957 164.05 <2e-16 ***
#> residual 0.95036 0.02159 44.02 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 1.485 on 997 degrees of freedom
#> Multiple R-squared: 0.9958, Adjusted R-squared: 0.9958
#> F-statistic: 1.175e+05 on 2 and 997 DF, p-value: < 2.2e-16
modelsummary(list(second_stage, second_stage_cf))| (1) | (2) | |
|---|---|---|
| (Intercept) | 11.991 | 11.991 |
| (5.767) | (0.398) | |
| new_endogenous | 3.210 | |
| (0.283) | ||
| endogenous | 3.210 | |
| (0.020) | ||
| residual | 0.950 | |
| (0.022) | ||
| Num.Obs. | 1000 | 1000 |
| R2 | 0.114 | 0.996 |
| R2 Adj. | 0.113 | 0.996 |
| AIC | 8977.0 | 3633.5 |
| BIC | 8991.8 | 3653.2 |
| Log.Lik. | -4485.516 | -1812.768 |
| F | 128.483 | 117473.460 |
| RMSE | 21.47 | 1.48 |
Nonlinear in endogenous variable
# 2SLS
first_stage = lm(endogenous_nonlinear ~ exogenous, data = my_data)
new_data = cbind(my_data, new_endogenous_nonlinear = predict(first_stage, my_data))
second_stage = lm(response_nonlinear ~ new_endogenous_nonlinear, data = new_data)
summary(second_stage)
#>
#> Call:
#> lm(formula = response_nonlinear ~ new_endogenous_nonlinear, data = new_data)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -101.26 -53.01 -13.50 39.33 376.16
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 11.7539 21.6478 0.543 0.587
#> new_endogenous_nonlinear 3.1253 0.5993 5.215 2.23e-07 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 70.89 on 998 degrees of freedom
#> Multiple R-squared: 0.02653, Adjusted R-squared: 0.02555
#> F-statistic: 27.2 on 1 and 998 DF, p-value: 2.234e-07
new_data_cf = cbind(my_data, residual = resid(first_stage))
second_stage_cf = lm(response_nonlinear ~ endogenous_nonlinear + residual, data = new_data_cf)
summary(second_stage_cf)
#>
#> Call:
#> lm(formula = response_nonlinear ~ endogenous_nonlinear + residual,
#> data = new_data_cf)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -12.8559 -0.8337 0.4429 1.3432 4.3147
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 11.75395 0.67012 17.540 < 2e-16 ***
#> endogenous_nonlinear 3.12525 0.01855 168.469 < 2e-16 ***
#> residual 0.13577 0.01882 7.213 1.08e-12 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 2.194 on 997 degrees of freedom
#> Multiple R-squared: 0.9991, Adjusted R-squared: 0.9991
#> F-statistic: 5.344e+05 on 2 and 997 DF, p-value: < 2.2e-16
modelsummary(list(second_stage, second_stage_cf))| (1) | (2) | |
|---|---|---|
| (Intercept) | 11.754 | 11.754 |
| (21.648) | (0.670) | |
| new_endogenous_nonlinear | 3.125 | |
| (0.599) | ||
| endogenous_nonlinear | 3.125 | |
| (0.019) | ||
| residual | 0.136 | |
| (0.019) | ||
| Num.Obs. | 1000 | 1000 |
| R2 | 0.027 | 0.999 |
| R2 Adj. | 0.026 | 0.999 |
| AIC | 11364.2 | 4414.7 |
| BIC | 11378.9 | 4434.4 |
| Log.Lik. | -5679.079 | -2203.371 |
| F | 27.196 | 534439.006 |
| RMSE | 70.82 | 2.19 |
Nonlinear in parameters
# 2SLS
first_stage = lm(endogenous ~ exogenous, data = my_data)
new_data = cbind(my_data, new_endogenous = predict(first_stage, my_data))
second_stage = lm(response_nonlinear_para ~ new_endogenous, data = new_data)
summary(second_stage)
#>
#> Call:
#> lm(formula = response_nonlinear_para ~ new_endogenous, data = new_data)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -1402.34 -462.21 -64.22 382.35 3090.62
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -1137.875 173.811 -6.547 9.4e-11 ***
#> new_endogenous 122.525 8.534 14.357 < 2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 647.7 on 998 degrees of freedom
#> Multiple R-squared: 0.1712, Adjusted R-squared: 0.1704
#> F-statistic: 206.1 on 1 and 998 DF, p-value: < 2.2e-16
new_data_cf = cbind(my_data, residual = resid(first_stage))
second_stage_cf = lm(response_nonlinear_para ~ endogenous_nonlinear + residual, data = new_data_cf)
summary(second_stage_cf)
#>
#> Call:
#> lm(formula = response_nonlinear_para ~ endogenous_nonlinear +
#> residual, data = new_data_cf)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -904.77 -154.35 -20.41 143.24 953.04
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 492.2494 32.3530 15.21 < 2e-16 ***
#> endogenous_nonlinear 23.5991 0.8741 27.00 < 2e-16 ***
#> residual 30.5914 3.7397 8.18 8.58e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 245.9 on 997 degrees of freedom
#> Multiple R-squared: 0.8806, Adjusted R-squared: 0.8804
#> F-statistic: 3676 on 2 and 997 DF, p-value: < 2.2e-16
modelsummary(list(second_stage, second_stage_cf))| (1) | (2) | |
|---|---|---|
| (Intercept) | -1137.875 | 492.249 |
| (173.811) | (32.353) | |
| new_endogenous | 122.525 | |
| (8.534) | ||
| endogenous_nonlinear | 23.599 | |
| (0.874) | ||
| residual | 30.591 | |
| (3.740) | ||
| Num.Obs. | 1000 | 1000 |
| R2 | 0.171 | 0.881 |
| R2 Adj. | 0.170 | 0.880 |
| AIC | 15788.6 | 13853.1 |
| BIC | 15803.3 | 13872.7 |
| Log.Lik. | -7891.307 | -6922.553 |
| F | 206.123 | 3676.480 |
| RMSE | 647.01 | 245.58 |
34.3.6 Fuller and Bias-Reduced IV
Fuller adjusts LIML for bias reduction.
fuller_model = ivreg(y ~ x_endo_1 | x_inst_1, data = base, method = "fuller", k = 1)
summary(fuller_model)
#>
#> Call:
#> ivreg(formula = y ~ x_endo_1 | x_inst_1, data = base, method = "fuller",
#> k = 1)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -1.2390 -0.3022 -0.0206 0.2772 1.0039
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 4.34586 0.08096 53.68 <2e-16 ***
#> x_endo_1 0.39848 0.01964 20.29 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.4075 on 148 degrees of freedom
#> Multiple R-Squared: 0.7595, Adjusted R-squared: 0.7578
#> Wald test: 411.6 on 1 and 148 DF, p-value: < 2.2e-1634.4 Asymptotic Properties of the IV Estimator
IV estimation provides consistent and asymptotically normal estimates of structural parameters under a specific set of assumptions. Understanding the asymptotic properties of the IV estimator requires clarity on the identification conditions and the large-sample behavior of the estimator.
Consider the linear structural model:
\[ Y = X \beta + u \]
Where:
\(Y\) is the dependent variable (\(n \times 1\))
\(X\) is a matrix of endogenous regressors (\(n \times k\))
\(u\) is the error term
\(\beta\) is the parameter vector of interest (\(k \times 1\))
Suppose we have a matrix of instruments \(Z\) (\(n \times m\)), with \(m \ge k\).
The IV estimator of \(\beta\) is:
\[ \hat{\beta}_{IV} = (Z'X)^{-1} Z'Y \]
Alternatively, when using 2SLS, this is equivalent to:
\[ \hat{\beta}_{2SLS} = (X'P_ZX)^{-1} X'P_ZY \]
Where:
- \(P_Z = Z (Z'Z)^{-1} Z'\) is the projection matrix onto the column space of \(Z\).
34.4.1 Consistency
For \(\hat{\beta}_{IV}\) to be consistent, the following conditions must hold as \(n \to \infty\):
- Instrument Exogeneity
\[ \mathbb{E}[Z'u] = 0 \]
Instruments must be uncorrelated with the structural error term.
Guarantees instrument validity.
- Instrument Relevance
\[ \mathrm{rank}(\mathbb{E}[Z'X]) = k \]
Instruments must be correlated with the endogenous regressors.
Ensures identification of \(\beta\).
If this fails, the model is underidentified, and \(\hat{\beta}_{IV}\) does not converge to the true \(\beta\).
- Random Sampling (IID Observations)
- \(\{(Y_i, X_i, Z_i)\}_{i=1}^n\) are independent and identically distributed (i.i.d.).
- In more general settings, stationarity and mixing conditions can relax this.
- Finite Moments
- \(\mathbb{E}[||Z||^2] < \infty\) and \(\mathbb{E}[||u||^2] < \infty\)
- Ensures Law of Large Numbers applies to sample moments.
If these conditions are satisfied: \[ \hat{\beta}_{IV} \overset{p}{\to} \beta \] This means the IV estimator is consistent.
34.4.2 Asymptotic Normality
In addition to consistency conditions, we require:
- Homoskedasticity (Optional but Simplifying)
\[ \mathbb{E}[u u' | Z] = \sigma^2 I \]
Simplifies variance estimation.
If violated, heteroskedasticity-robust variance estimators must be used.
- Central Limit Theorem Conditions
- Sample moments must satisfy a CLT: \[ \sqrt{n} \left( \frac{1}{n} \sum_{i=1}^n Z_i u_i \right) \overset{d}{\to} N(0, \Omega) \] Where \(\Omega = \mathbb{E}[Z_i Z_i' u_i^2]\).
Under the above conditions: \[ \sqrt{n}(\hat{\beta}_{IV} - \beta) \overset{d}{\to} N(0, V) \]
Where the asymptotic variance-covariance matrix \(V\) is: \[ V = (Q_{ZX})^{-1} Q_{Zuu} (Q_{ZX}')^{-1} \] With:
\(Q_{ZX} = \mathbb{E}[Z_i X_i']\)
\(Q_{Zuu} = \mathbb{E}[Z_i Z_i' u_i^2]\)
34.4.3 Asymptotic Efficiency
- Optimal Instrument Choice
- Among all IV estimators, 2SLS is efficient when the instrument matrix \(Z\) contains all relevant information.
- Generalized Method of Moments (GMM) can deliver efficiency gains in the presence of heteroskedasticity, by optimally weighting the moment conditions.
GMM Estimator
\[ \hat{\beta}_{GMM} = \arg \min_{\beta} \left( \frac{1}{n} \sum_{i=1}^n Z_i (Y_i - X_i' \beta) \right)' W \left( \frac{1}{n} \sum_{i=1}^n Z_i (Y_i - X_i' \beta) \right) \]
Where \(W\) is an optimal weighting matrix, typically:
\[ W = \Omega^{-1} \]
Result
- If \(Z\) is overidentified (\(m > k\)), GMM can be more efficient than 2SLS.
- When instruments are exactly identified (\(m = k\)), IV, 2SLS, and GMM coincide.
Summary Table of Conditions
| Condition | Requirement | Purpose |
|---|---|---|
| Instrument Exogeneity | \(\mathbb{E}[Z'u] = 0\) | Instrument validity |
| Instrument Relevance | \(\mathrm{rank}(\mathbb{E}[Z'X]) = k\) | Model identification |
| Random Sampling | IID (or stationary and mixing) | LLN and CLT applicability |
| Finite Second Moments | \(\mathbb{E}[||Z||^2] < \infty\), etc. | LLN and CLT applicability |
| Homoskedasticity (optional) | \(\mathbb{E}[u u' | Z] = \sigma^2 I\) | Simplifies variance formulas |
| Optimal Weighting | \(W = \Omega^{-1}\) in GMM | Asymptotic efficiency |
34.5 Inference
Inference in IV models, particularly when instruments are weak, presents serious challenges that can undermine standard testing and confidence interval procedures. In this section, we explore the core issues of IV inference under weak instruments, discuss the standard and alternative approaches, and outline practical guidelines for applied research.
Consider the just-identified linear IV model:
\[ Y = \beta X + u \]
where:
\(X\) is endogenous: \(\text{Cov}(X, u) \neq 0\).
-
\(Z\) is an instrumental variable satisfying:
Relevance: \(\text{Cov}(Z, X) \neq 0\).
Exogeneity: \(\text{Cov}(Z, u) = 0\).
The IV estimator of \(\beta\) is consistent under these assumptions.
A commonly used approach for inference is the t-ratio method, constructing a 95% confidence interval as:
\[ \hat{\beta} \pm 1.96 \sqrt{\hat{V}_N(\hat{\beta})} \]
However, this approach is invalid when instruments are weak. Specifically:
The t-ratio does not follow a standard normal distribution under weak instruments.
Confidence intervals based on this method can severely under-cover the true parameter.
Hypothesis tests can over-reject, even in large samples.
This problem was first systematically identified by Staiger and Stock (1997) and Dufour (1997). Weak instruments create distortions in the finite-sample distribution of \(\hat{\beta}\).
Common Practices and Misinterpretations
- Overreliance on t-Ratio Tests
- Popular but problematic when instruments are weak.
- Known to over-reject null hypotheses and under-cover confidence intervals.
- Documented extensively by Nelson and Startz (1990), Bound, Jaeger, and Baker (1995), Dufour (1997), and Lee et al. (2022).
- Weak Instrument Diagnostics
- First-Stage F-Statistic:
- Rule of thumb: \(F > 10\) often used but simplistic and misleading.
- More accurate critical values provided by Stock and Yogo (2005).
- For 95% coverage, \(F > 16.38\) is often cited (Staiger and Stock 1997).
- Misinterpretations and Pitfalls
- Mistakenly interpreting \(\hat{\beta} \pm 1.96 \times \hat{SE}\) as a 95% CI when the instrument is weak, Staiger and Stock (1997) show that under \(F > 16.38\), the nominal 95% CI may only offer 85% coverage.
- Pretesting for weak instruments can exacerbate inference problems (A. R. Hall, Rudebusch, and Wilcox 1996).
- Selective model specification based on weak instrument diagnostics may introduce additional distortions (I. Andrews, Stock, and Sun 2019).
34.5.1 Weak Instruments Problem
An alternative statistic accounts for weak instrument issues by adjusting the standard Anderson-Rubin (AR) test:
\[ \hat{t}^2 = \hat{t}^2_{AR} \times \frac{1}{1 - \hat{\rho} \frac{\hat{t}_{AR}}{\hat{f}} + \frac{\hat{t}^2_{AR}}{\hat{f}^2}} \]
Where:
\(\hat{t}^2_{AR} \sim \chi^2(1)\) under the null, even with weak instruments (T. W. Anderson and Rubin 1949).
\(\hat{t}_{AR} = \dfrac{\hat{\pi}(\hat{\beta} - \beta_0)}{\sqrt{\hat{V}_N (\hat{\pi} (\hat{\beta} - \beta_0))}} \sim N(0,1)\).
\(\hat{f} = \dfrac{\hat{\pi}}{\sqrt{\hat{V}_N(\hat{\pi})}}\) measures instrument strength (first-stage F-stat).
\(\hat{\pi}\) is the coefficient from the first-stage regression of \(X\) on \(Z\).
\(\hat{\rho} = \text{Cov}(Zv, Zu)\) captures the correlation between first-stage residuals and \(u\).
Implications
- Even in large samples, \(\hat{t}^2 \neq \hat{t}^2_{AR}\) because the adjustment term does not converge to zero unless instruments are strong and \(\rho = 0\).
- The distribution of \(\hat{t}\) does not match the standard normal but follows a more complex distribution described by Staiger and Stock (1997) and Stock and Yogo (2005).
The divergence between \(\hat{t}^2\) and \(\hat{t}^2_{AR}\) depends on:
- Instrument Strength (\(\pi\)): Higher correlation between \(Z\) and \(X\) mitigates the problem.
- First-Stage F-statistic (\(E(F)\)): A weak first-stage regression increases the bias and distortion.
- Endogeneity Level (\(|\rho|\)): Greater correlation between \(X\) and \(u\) exacerbates inference errors.
| Scenario | Conditions | Inference Quality |
|---|---|---|
| Worst Case | \(\pi = 0\), \(|\rho| = 1\) | \(\hat{\beta} \pm 1.96 \times SE\) fails; Type I error = 100% |
| Best Case | \(\rho = 0\) (No endogeneity) or very large \(\hat{f}\) (strong \(Z\)) | Standard inference works; intervals cover \(\beta\) with correct rate |
| Intermediate Case | Moderate \(\pi\), \(\rho\), and \(F\) | Coverage and Type I error lie between extremes; standard inference risky |
34.5.2 Solutions and Approaches for Valid Inference
- Assume the Problem Away (Risky Assumptions)
- High First-Stage F-statistic:
- Require \(E(F) > 142.6\) for near-validity (Lee et al. 2022).
- While the first-stage \(F\) is observable, this threshold is high and often impractical.
- Low Endogeneity:
- Assume \(|\rho| < 0.565\) Lee et al. (2022). In other words, we assume endogeneity to be less than moderat level.
- This undermines the motivation for IV in the first place, which exists precisely because of suspected endogeneity.
- High First-Stage F-statistic:
- Confront the Problem Directly (Robust Methods)
-
Anderson-Rubin (AR) Test (T. W. Anderson and Rubin 1949):
- Valid under weak instruments.
- Tests whether \(Z\) explains variation in \(Y - \beta_0 X\).
-
tF Procedure (Lee et al. 2022):
- Combines t-statistics and F-statistics in a unified testing framework.
- Offers valid inference in presence of weak instruments.
-
Andrews-Kolesár (AK) Procedure (J. Angrist and Kolesár 2023):
- Provides uniformly valid confidence intervals for \(\beta\).
- Allows for weak instruments and arbitrary heteroskedasticity.
- Especially useful in overidentified settings.
-
Anderson-Rubin (AR) Test (T. W. Anderson and Rubin 1949):
34.5.3 Anderson-Rubin Approach
The Anderson-Rubin (AR) test, originally proposed by T. W. Anderson and Rubin (1949), remains one of the most robust inferential tools in the context of instrumental variable estimation, particularly when instruments are weak or endogenous regressors exhibit complex error structures.
The AR test directly evaluates the joint null hypothesis that:
\[ H_0: \beta = \beta_0 \]
by testing whether the instruments explain any variation in the residuals \(Y - \beta_0 X\). Under the null, the model becomes:
\[ Y - \beta_0 X = u \]
Given that \(\text{Cov}(Z, u) = 0\) (by the IV exogeneity assumption), the test regresses \((Y - \beta_0 X)\) on \(Z\). The test statistic is constructed as:
\[ AR(\beta_0) = \frac{(Y - \beta_0 X)' P_Z (Y - \beta_0 X)}{\hat{\sigma}^2} \]
- \(P_Z\) is the projection matrix onto the column space of \(Z\): \(P_Z = Z (Z'Z)^{-1} Z'\).
- \(\hat{\sigma}^2\) is an estimate of the error variance (under homoskedasticity).
Under \(H_0\), the statistic follows a chi-squared distribution:
\[ AR(\beta_0) \sim \chi^2(q) \]
where \(q\) is the number of instruments (1 in a just-identified model).
Key Properties of the AR Test
- Robust to Weak Instruments:
- The AR test does not rely on the strength of the instruments.
- Its distribution under the null hypothesis remains valid even when the instruments are weak (Staiger and Stock 1997).
- Robust to Non-Normality and Homoskedastic Errors:
- Maintains correct Type I error rates even under non-normal errors (Staiger and Stock 1997).
- Optimality properties under homoskedastic errors are established in D. W. Andrews, Moreira, and Stock (2006) and M. J. Moreira (2009).
- Robust to Heteroskedasticity, Clustering, and Autocorrelation:
- The AR test has been generalized to account for heteroskedasticity, clustered errors, and autocorrelation (Stock and Wright 2000; H. Moreira and Moreira 2019).
- Valid inference is possible when combined with heteroskedasticity-robust variance estimators or cluster-robust techniques.
| Setting | Validity | Reference |
|---|---|---|
| Non-Normal, Homoskedastic Errors | Valid without distributional assumptions | (Staiger and Stock 1997) |
| Heteroskedastic Errors | Generalized AR test remains valid; robust variance estimation recommended | (Stock and Wright 2000) |
| Clustered or Autocorrelated Errors | Extensions available using cluster-robust and HAC variance estimators | (H. Moreira and Moreira 2019) |
| Optimality under Homoskedasticity | AR test minimizes Type II error among invariant tests | (D. W. Andrews, Moreira, and Stock 2006; M. J. Moreira 2009) |
The AR test is relatively simple to implement and is available in most econometric software. Here’s an intuitive step-by-step breakdown:
- Specify the null hypothesis value \(\beta_0\).
- Compute the residual \(u = Y - \beta_0 X\).
- Regress \(u\) on \(Z\) and obtain the \(R^2\) from this regression.
- Compute the test statistic:
\[ AR(\beta_0) = \frac{R^2 \cdot n}{q} \]
(For a just-identified model with a single instrument, \(q=1\).)
- Compare \(AR(\beta_0)\) to the \(\chi^2(q)\) distribution to determine significance.
library(ivDiag)
# AR test (robust to weak instruments)
# example by the package's authors
ivDiag::AR_test(
data = rueda,
Y = "e_vote_buying",
# treatment
D = "lm_pob_mesa",
# instruments
Z = "lz_pob_mesa_f",
controls = c("lpopulation", "lpotencial"),
cl = "muni_code",
CI = FALSE
)
#> $Fstat
#> F df1 df2 p
#> 48.4768 1.0000 4350.0000 0.0000
g <- ivDiag::ivDiag(
data = rueda,
Y = "e_vote_buying",
D = "lm_pob_mesa",
Z = "lz_pob_mesa_f",
controls = c("lpopulation", "lpotencial"),
cl = "muni_code",
cores = 4,
bootstrap = FALSE
)
g$AR
#> $Fstat
#> F df1 df2 p
#> 48.4768 1.0000 4350.0000 0.0000
#>
#> $ci.print
#> [1] "[-1.2626, -0.7073]"
#>
#> $ci
#> [1] -1.2626 -0.7073
#>
#> $bounded
#> [1] TRUE
ivDiag::plot_coef(g)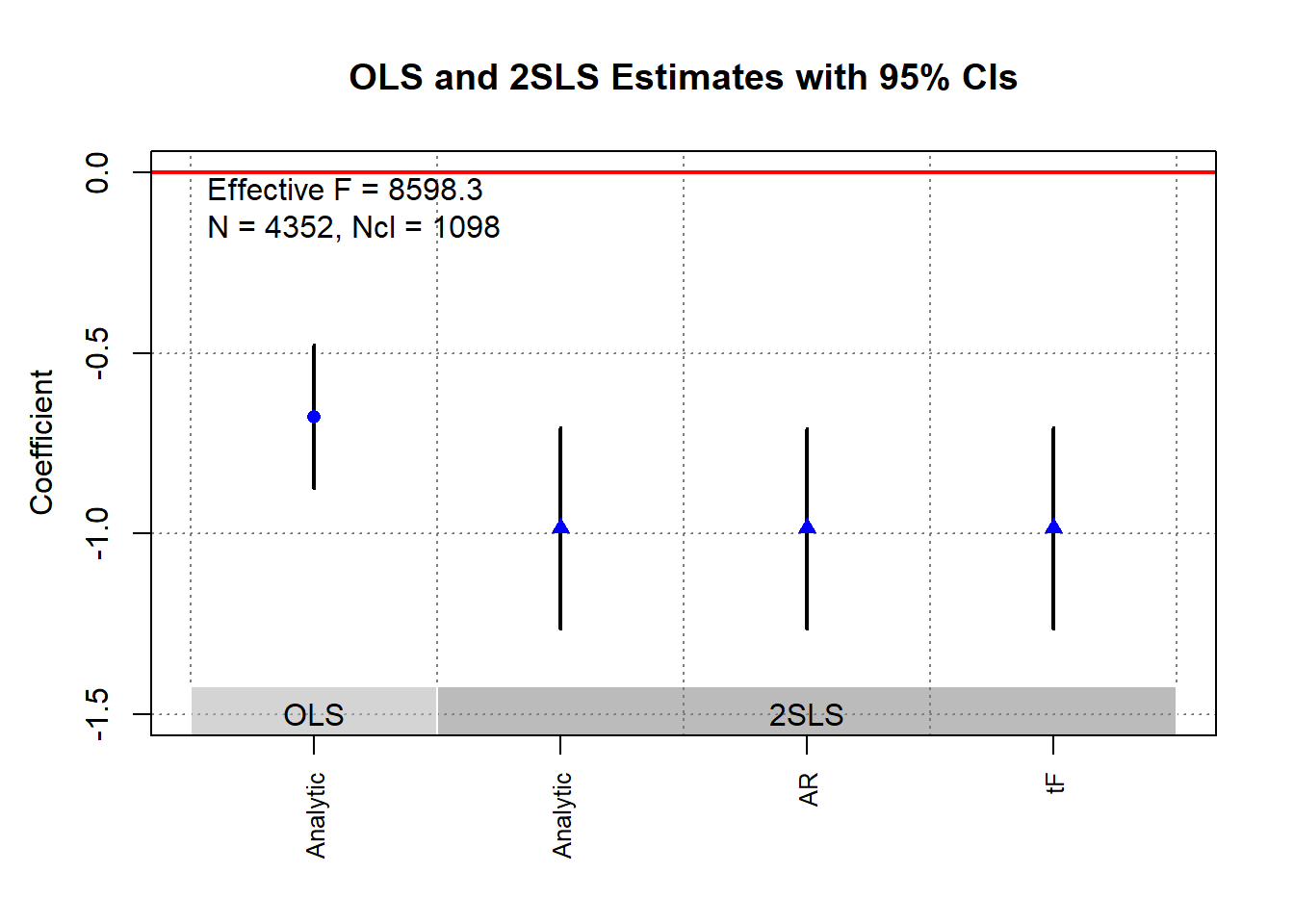
34.5.4 tF Procedure
Lee et al. (2022) introduce the tF procedure, an inference method specifically designed for just-identified IV models (single endogenous regressor and single instrument). It addresses the shortcomings of traditional 2SLS \(t\)-tests under weak instruments and offers a solution that is conceptually familiar to researchers trained in standard econometric practices.
Unlike the Anderson-Rubin test, which inverts hypothesis tests to form confidence sets, the tF procedure adjusts standard \(t\)-statistics and standard errors directly, making it a more intuitive extension of traditional hypothesis testing.
The tF procedure is widely applicable in settings where just-identified IV models arise, including:
Randomized controlled trials with imperfect compliance
(e.g., Local Average Treatment Effects in G. W. Imbens and Angrist (1994)).Fuzzy Regression Discontinuity Designs
(e.g., Lee and Lemieux (2010)).Fuzzy Regression Kink Designs
(e.g., (Card et al. 2015)).
A comparison of the AR approach and the tF procedure can be found in I. Andrews, Stock, and Sun (2019).
| Feature | Anderson-Rubin | tF Procedure |
|---|---|---|
| Robustness to Weak IV | Yes (valid under weak instruments) | Yes (valid under weak instruments) |
| Finite Confidence Intervals | No (interval becomes infinite for \(F \le 3.84\)) | Yes (finite intervals for all \(F\) values) |
| Interval Length | Often longer, especially when \(F\) is moderate (e.g., \(F = 16\)) | Typically shorter than AR intervals for \(F > 3.84\) |
| Ease of Interpretation | Requires inverting tests; less intuitive | Directly adjusts \(t\)-based standard errors; more intuitive |
| Computational Simplicity | Moderate (inversion of hypothesis tests) | Simple (multiplicative adjustment to standard errors) |
- With \(F > 3.84\), the AR test’s expected interval length is infinite, whereas the tF procedure guarantees finite intervals, making it superior in practical applications with weak instruments.
The tF procedure adjusts the conventional 2SLS \(t\)-ratio for the first-stage F-statistic strength. Instead of relying on a pre-testing threshold (e.g., \(F > 10\)), the tF approach provides a smooth adjustment to the standard errors.
Key Features:
- Adjusts the 2SLS \(t\)-ratio based on the observed first-stage F-statistic.
- Applies different adjustment factors for different significance levels (e.g., 95% and 99%).
- Remains valid even when the instrument is weak, offering finite confidence intervals even when the first-stage F-statistic is low.
Advantages of the tF Procedure
- Smooth Adjustment for First-Stage Strength
The tF procedure smoothly adjusts inference based on the observed first-stage F-statistic, avoiding the need for arbitrary pre-testing thresholds (e.g., \(F > 10\)).
-
It produces finite and usable confidence intervals even when the first-stage F-statistic is low:
\[ F > 3.84 \]
-
This threshold aligns with the critical value of 3.84 for a 95% Anderson-Rubin confidence interval, but with a crucial advantage:
- The AR interval becomes unbounded (i.e., infinite length) when \(F \le 3.84\).
- The tF procedure, in contrast, still provides a finite confidence interval, making it more practical in weak instrument cases.
- Clear and Interpretable Confidence Levels
-
The tF procedure offers transparent confidence intervals that:
Directly incorporate the impact of first-stage instrument strength on the critical values used for inference.
Mirror the distortion-free properties of robust methods like the Anderson-Rubin test, but remain closer in spirit to conventional \(t\)-based inference.
Researchers can interpret tF-based 95% and 99% confidence intervals using familiar econometric tools, without needing to invert hypothesis tests or construct confidence sets.
- Robustness to Common Error Structures
-
The tF procedure remains robust in the presence of:
- Heteroskedasticity
- Clustering
- Autocorrelation
-
No additional adjustments are necessary beyond the use of a robust variance estimator for both:
- The first-stage regression
- The second-stage IV regression
As long as the same robust variance estimator is applied consistently, the tF adjustment maintains valid inference without imposing additional computational complexity.
- Applicability to Published Research
-
One of the most powerful features of the tF procedure is its flexibility for re-evaluating published studies:
Researchers only need the reported first-stage F-statistic and standard errors from the 2SLS estimates.
No access to the original data is required to recalculate confidence intervals or test statistical significance using the tF adjustment.
-
This makes the tF procedure particularly valuable for meta-analyses, replications, and robustness checks of published IV studies, where:
- Raw data may be unavailable, or
- Replication costs are high.
Consider the linear IV model with additional covariates \(W\):
\[ Y = X \beta + W \gamma + u \]
\[ X = Z \pi + W \xi + \nu \]
Where:
\(Y\): Outcome variable.
\(X\): Endogenous regressor of interest.
\(Z\): Instrumental variable (single instrument case).
\(W\): Vector of exogenous controls, possibly including an intercept.
\(u\), \(\nu\): Error terms.
Key Statistics:
-
\(t\)-ratio for the IV estimator:
\[ \hat{t} = \frac{\hat{\beta} - \beta_0}{\sqrt{\hat{V}_N (\hat{\beta})}} \]
-
\(t\)-ratio for the first-stage coefficient:
\[ \hat{f} = \frac{\hat{\pi}}{\sqrt{\hat{V}_N (\hat{\pi})}} \]
-
First-stage F-statistic:
\[ \hat{F} = \hat{f}^2 \]
where
- \(\hat{\beta}\): Instrumental variable estimator.
- \(\hat{V}_N (\hat{\beta})\): Estimated variance of \(\hat{\beta}\), possibly robust to deal with non-iid errors.
- \(\hat{t}\): \(t\)-ratio under the null hypothesis.
- \(\hat{f}\): \(t\)-ratio under the null hypothesis of \(\pi=0\).
Under traditional asymptotics large samples, the \(t\)-ratio statistic follows:
\[ \hat{t}^2 \to^d t^2 \]
With critical values:
\(\pm 1.96\) for a 5% significance test.
\(\pm 2.58\) for a 1% significance test.
However, in IV settings (particularly with weak instruments):
The distribution of the \(t\)-statistic is distorted (i.e., \(t\)-distribution might not be normal), even in large samples.
The distortion arises because the strength of the instrument (\(F\)) and the degree of endogeneity (\(\rho\)) affect the \(t\)-distribution.
Stock and Yogo (2005) provide a formula to quantify this distortion (in the just-identified case) for Wald test statistics using 2SLS.:
\[ t^2 = f + t_{AR} + \rho f t_{AR} \]
Where:
\(\hat{f} \to^d f\)
\(\bar{f} = \dfrac{\pi}{\sqrt{\dfrac{1}{N} AV(\hat{\pi})}}\) and \(AV(\hat{\pi})\) is the asymptotic variance of \(\hat{\pi}\)
\(t_{AR}\) is asymptotically standard normal (\(AR = t^2_{AR}\))
\(\rho\) measures the correlation (degree of endogeneity) between \(Zu\) and \(Z\nu\) (when data are homoskedastic, \(\rho\) is the correlation between \(u\) and \(\nu\)).
Implications:
- For low \(\rho\) (\(\rho \in [0, 0.5]\)), rejection probabilities can be below nominal levels.
- For high \(\rho\) (\(\rho = 0.8\)), rejection rates can be inflated, e.g., 13% rejection at a nominal 5% significance level.
- Reliance on standard \(t\)-ratios leads to incorrect test sizes and invalid confidence intervals.
The tF procedure corrects for these distortions by adjusting the standard error of the 2SLS estimator based on the observed first-stage F-statistic.
Steps:
- Estimate \(\hat{\beta}\) and its conventional SE from 2SLS.
- Compute the first-stage \(\hat{F}\).
- Multiply the conventional SE by an adjustment factor, which depends on \(\hat{F}\) and the desired confidence level.
- Compute new \(t\)-ratios and construct confidence intervals using standard critical values (e.g., \(\pm 1.96\) for 95% CI).
Lee et al. (2022) refer to the adjusted standard errors as “0.05 tF SE” (for a 5% significance level) and “0.01 tF SE” (for 1%).
Lee et al. (2022) conducted a review of recent single-instrument studies in the American Economic Review.
Key Findings:
- For at least 25% of the examined specifications:
- tF-adjusted confidence intervals were 49% longer at the 5% level.
- tF-adjusted confidence intervals were 136% longer at the 1% level.
- Even among specifications with \(F > 10\) and \(t > 1.96\):
- Approximately 25% became statistically insignificant at the 5% level after applying the tF adjustment.
Takeaway:
- The tF procedure can substantially alter inference conclusions.
- Published studies can be re-evaluated with the tF method using only the reported first-stage F-statistics, without requiring access to the underlying microdata.
library(ivDiag)
g <- ivDiag::ivDiag(
data = rueda,
Y = "e_vote_buying",
D = "lm_pob_mesa",
Z = "lz_pob_mesa_f",
controls = c("lpopulation", "lpotencial"),
cl = "muni_code",
cores = 4,
bootstrap = FALSE
)
g$tF
#> F cF Coef SE t CI2.5% CI97.5% p-value
#> 8598.3264 1.9600 -0.9835 0.1424 -6.9071 -1.2626 -0.7044 0.0000
# example in fixest package
library(fixest)
library(tidyverse)
base = iris
names(base) = c("y", "x1", "x_endo_1", "x_inst_1", "fe")
set.seed(2)
base$x_inst_2 = 0.2 * base$y + 0.2 * base$x_endo_1 + rnorm(150, sd = 0.5)
base$x_endo_2 = 0.2 * base$y - 0.2 * base$x_inst_1 + rnorm(150, sd = 0.5)
est_iv = feols(y ~ x1 | x_endo_1 + x_endo_2 ~ x_inst_1 + x_inst_2, base)
est_iv
#> TSLS estimation - Dep. Var.: y
#> Endo. : x_endo_1, x_endo_2
#> Instr. : x_inst_1, x_inst_2
#> Second stage: Dep. Var.: y
#> Observations: 150
#> Standard-errors: IID
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 1.831380 0.411435 4.45121 1.6844e-05 ***
#> fit_x_endo_1 0.444982 0.022086 20.14744 < 2.2e-16 ***
#> fit_x_endo_2 0.639916 0.307376 2.08186 3.9100e-02 *
#> x1 0.565095 0.084715 6.67051 4.9180e-10 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> RMSE: 0.398842 Adj. R2: 0.725033
#> F-test (1st stage), x_endo_1: stat = 903.1628, p < 2.2e-16 , on 2 and 146 DoF.
#> F-test (1st stage), x_endo_2: stat = 3.2583, p = 0.041268, on 2 and 146 DoF.
#> Wu-Hausman: stat = 6.7918, p = 0.001518, on 2 and 144 DoF.
res_est_iv <- est_iv$coeftable |>
rownames_to_column()
coef_of_interest <-
res_est_iv[res_est_iv$rowname == "fit_x_endo_1", "Estimate"]
se_of_interest <-
res_est_iv[res_est_iv$rowname == "fit_x_endo_1", "Std. Error"]
fstat_1st <- fitstat(est_iv, type = "ivf1")[[1]]$stat
# To get the correct SE based on 1st-stage F-stat (This result is similar without adjustment since F is large)
# the results are the new CIS and p.value
tF(coef = coef_of_interest, se = se_of_interest, Fstat = fstat_1st) |>
causalverse::nice_tab(5)
#> F cF Coef SE t CI2.5. CI97.5. p.value
#> 1 903.1628 1.96 0.445 0.0221 20.1474 0.4017 0.4883 0
# We can try to see a different 1st-stage F-stat and how it changes the results
tF(coef = coef_of_interest, se = se_of_interest, Fstat = 2) |>
causalverse::nice_tab(5)
#> F cF Coef SE t CI2.5. CI97.5. p.value
#> 1 2 18.66 0.445 0.0221 20.1474 0.0329 0.8571 0.034334.5.5 AK Approach
J. Angrist and Kolesár (2024) offer a reappraisal of just-identified IV models, focusing on the finite-sample properties of conventional inference in cases where a single instrument is used for a single endogenous variable. Their findings challenge some of the more pessimistic views about weak instruments and inference distortions in microeconometric applications.
Rather than propose a new estimator or test, Angrist and Kolesár provide a framework and rationale supporting the validity of traditional just-ID IV inference in many practical settings. Their insights clarify when conventional t-tests and confidence intervals can be trusted, and they offer practical guidance on first-stage pretesting, bias reduction, and endogeneity considerations.
AK apply their framework to three canonical studies:
- J. D. Angrist and Krueger (1991) - Education returns
- J. D. Angrist and Evans (1998) - Family size and female labor supply
- J. D. Angrist and Lavy (1999) - Class size effects
Findings:
Endogeneity (\(\rho\)) in these studies is moderate (typically \(|\rho| < 0.47\)).
Conventional t-tests and confidence intervals work reasonably well.
In many micro applications, theoretical bounds on causal effects and plausible OVB scenarios limit \(\rho\), supporting the validity of conventional inference.
Key Contributions of the AK Approach
Reassessing Bias and Coverage:
AK demonstrate that conventional IV estimates and t-tests in just-ID IV models often perform better than theory might suggest—provided the degree of endogeneity (\(\rho\)) is moderate, and the first-stage F-statistic is not extremely weak.-
First-Stage Sign Screening:
- They propose sign screening as a simple, costless strategy to halve the median bias of IV estimators.
- Screening on the sign of the estimated first-stage coefficient (i.e., using only samples where the first-stage estimate has the correct sign) improves the finite-sample performance of just-ID IV estimates without degrading confidence interval coverage.
-
Bias-Minimizing Screening Rule:
- AK show that setting the first-stage t-statistic threshold \(c = 0\), i.e., requiring only the correct sign of the first-stage estimate, minimizes median bias while preserving conventional coverage properties.
-
Practical Implication:
- They argue that conventional just-ID IV inference, including t-tests and confidence intervals, is likely valid in most microeconometric applications, especially where theory or institutional knowledge suggests the direction of the first-stage relationship.
34.5.5.1 Model Setup and Notation
AK adopt a reduced-form and first-stage specification for just-ID IV models:
\[ \begin{aligned} Y_i &= Z_i \delta + X_i' \psi_1 + u_i \\ D_i &= Z_i \pi + X_i' \psi_2 + v_i \end{aligned} \] where
- \(Y_i\): Outcome variable
- \(D_i\): Endogenous treatment variable
- \(Z_i\): Instrumental variable (single instrument)
- \(X_i\): Control variables
- \(u_i, v_i\): Error terms
Parameter of Interest:
\[ \beta = \frac{\delta}{\pi} \]
34.5.5.2 Endogeneity and Instrument Strength
AK characterize the two key parameters governing finite-sample inference:
Instrument Strength:
\[ E[F] = \frac{\pi^2}{\sigma^2_{\hat{\pi}}} + 1 \]
(Expected value of the first-stage F-statistic.)Endogeneity:
\[ \rho = \text{cor}(\hat{\delta} - \hat{\pi} \beta, \hat{\pi}) \]
Measures the degree of correlation between reduced-form and first-stage residuals (or between \(u\) and \(v\) under homoskedasticity).
Key Insight:
For \(\rho < 0.76\), the coverage of conventional 95% confidence intervals is distorted by less than 5%, regardless of the first-stage F-statistic.
34.5.5.3 First-Stage Sign Screening
AK argue that pre-screening based on the sign of the first-stage estimate (\(\hat{\pi}\)) offers bias reduction without compromising confidence interval coverage.
Screening Rule:
- Screen if \(\hat{\pi} > 0\)
(or \(\hat{\pi} < 0\) if the theoretical sign is negative).
Results:
- Halves median bias of the IV estimator.
- No degradation of confidence interval coverage.
This screening approach:
Avoids the pitfalls of pre-testing based on first-stage F-statistics (which can exacerbate bias and distort inference).
Provides a “free lunch”: bias reduction with no coverage cost.
34.5.5.4 Rejection Rates and Confidence Interval Coverage
- Rejection rates of conventional t-tests stay close to the nominal level (5%) if \(|\rho| < 0.76\), independent of instrument strength.
- For \(|\rho| < 0.565\), conventional t-tests exhibit no over-rejection, aligning with findings from Lee et al. (2022).
Comparison with AR and tF Procedures:
| Approach | Bias Reduction | Coverage | CI Length (F > 3.84) |
|---|---|---|---|
| AK Sign Screening | Halves median bias | Near-nominal | Finite |
| AR Test | No bias (inversion method) | Exact | Infinite |
| tF Procedure | Bias adjusted | Near-nominal | Longer than AK (especially for moderate F) |
34.6 Testing Assumptions
We are interested in estimating the causal effect of an endogenous regressor \(X_2\) on an outcome variable \(Y\), using instrumental variables \(Z\) to address endogeneity.
The structural model of interest is:
\[ Y = \beta_1 X_1 + \beta_2 X_2 + \epsilon \]
- \(X_1\): Exogenous regressors
- \(X_2\): Endogenous regressor(s)
- \(Z\): Instrumental variables
If \(Z\) satisfies the relevance and exogeneity assumptions, we can identify \(\beta_2\) as:
\[ \beta_2 = \frac{Cov(Z, Y)}{Cov(Z, X_2)} \]
Alternatively, in terms of reduced form and first stage estimates:
- Reduced Form (effect of \(Z\) on \(Y\)):
\[ \rho = \frac{Cov(Y, Z)}{Var(Z)} \]
- First Stage (effect of \(Z\) on \(X_2\)):
\[ \pi = \frac{Cov(X_2, Z)}{Var(Z)} \]
- IV Estimate:
\[ \beta_2 = \frac{Cov(Y,Z)}{Cov(X_2, Z)} = \frac{\rho}{\pi} \]
To interpret \(\beta_2\) as the causal effect of \(X_2\) on \(Y\), the following assumptions must hold:
34.6.1 Relevance Assumption
In IV estimation, instrument relevance ensures that the instrument(s) \(Z\) can explain sufficient variation in the endogenous regressor(s) \(X_2\) to identify the structural equation:
\[ Y = \beta_1 X_1 + \beta_2 X_2 + \epsilon \]
The relevance condition requires that the instrument(s) \(Z\) be correlated with the endogenous variable(s) \(X_2\), conditional on other covariates \(X_1\). Formally:
\[ Cov(Z, X_2) \ne 0 \]
Or, in matrix notation for multiple instruments and regressors, the matrix of correlations (or more generally, the projection matrix) between \(Z\) and \(X_2\) must be of full column rank. This guarantees that \(Z\) has non-trivial explanatory power for \(X_2\).
An equivalent condition in terms of population moment conditions is that:
\[ E[Z' (X_2 - E[X_2 | Z])] \ne 0 \]
This condition ensures the identification of \(\beta_2\). Without it, the IV estimator would be undefined due to division by zero in its ratio form:
\[ \hat{\beta}_2^{IV} = \frac{Cov(Z, Y)}{Cov(Z, X_2)} \]
The first-stage regression operationalizes the relevance assumption:
\[ X_2 = Z \pi + X_1 \gamma + u \]
- \(\pi\): Vector of first-stage coefficients, measuring the effect of instruments on the endogenous regressor(s).
- \(u\): First-stage residual.
Identification of \(\beta_2\) requires that \(\pi \ne 0\). If \(\pi = 0\), the instrument has no explanatory power for \(X_2\), and the IV procedure collapses.
34.6.1.1 Weak Instruments
Even when \(Cov(Z, X_2) \ne 0\), weak instruments pose a serious problem in finite samples:
- Bias: The IV estimator becomes biased in the direction of the OLS estimator.
- Size distortion: Hypothesis tests can have inflated Type I error rates.
- Variance: Estimates become highly variable and unreliable.
Asymptotic vs. Finite Sample Problems
- IV estimators are consistent as \(n \to \infty\) if the relevance condition holds.
- With weak instruments, convergence can be so slow that finite-sample behavior is practically indistinguishable from inconsistency.
Boundaries between relevance and strength are thus critical in applied work.
34.6.1.2 First-Stage F-Statistic
In a single endogenous regressor case, the first-stage F-statistic is the standard test for instrument strength.
First-Stage Regression:
\[ X_2 = Z \pi + X_1 \gamma + u \]
We test:
\[ \begin{aligned} H_0&: \pi = 0 \quad \text{(Instruments have no explanatory power)} \\ H_1&: \pi \ne 0 \quad \text{(Instruments explain variation in $X_2$)} \end{aligned} \]
F-Statistic Formula:
\[ F = \frac{(SSR_r - SSR_{ur}) / q}{SSR_{ur} / (n - k - 1)} \]
- \(SSR_r\): Sum of squared residuals from the restricted model (no instruments).
- \(SSR_{ur}\): Sum of squared residuals from the unrestricted model (with instruments).
- \(q\): Number of excluded instruments (restrictions tested).
- \(n\): Number of observations.
- \(k\): Number of control variables.
Interpretation:
- A rule of thumb (Staiger and Stock 1997): If \(F < 10\), instruments are weak.
- However, Lee et al. (2022) criticizes this threshold, advocating for model-specific diagnostics.
- M. J. Moreira (2003) proposes the Conditional Likelihood Ratio test for inference under weak instruments (D. W. Andrews, Moreira, and Stock 2008).
Use linearHypothesis() in R to test instrument relevance.
34.6.1.3 Cragg-Donald Test
The Cragg-Donald statistic is essentially the same as the Wald statistic of the joint significance of the instruments in the first stage (Cragg and Donald 1993), and it’s used specifically when you have multiple endogenous regressors. It’s calculated as:
\[ CD = n \times (R_{ur}^2 - R_r^2) \]
where:
\(R_{ur}^2\) and \(R_r^2\) are the R-squared values from the unrestricted and restricted models respectively.
\(n\) is the number of observations.
For one endogenous variable, the Cragg-Donald test results should align closely with those from Stock and Yogo. The Anderson canonical correlation test, a likelihood ratio test, also works under similar conditions, contrasting with Cragg-Donald’s Wald statistic approach. Both are valid with one endogenous variable and at least one instrument.
library(cragg)
library(AER) # for dataaset
data("WeakInstrument")
cragg_donald(
# control variables
X = ~ 1,
# endogeneous variables
D = ~ x,
# instrument variables
Z = ~ z,
data = WeakInstrument
)
#> Cragg-Donald test for weak instruments:
#>
#> Data: WeakInstrument
#> Controls: ~1
#> Treatments: ~x
#> Instruments: ~z
#>
#> Cragg-Donald Statistic: 4.566136
#> Df: 198Large CD statistic implies that the instruments are strong, but not in our case here. But to judge it against some critical value, we have to look at Stock-Yogo
34.6.1.4 Stock-Yogo
The Stock-Yogo test does not directly compute a statistic like the F-test or Cragg-Donald, but rather uses pre-computed critical values to assess the strength of instruments. It often uses the eigenvalues derived from the concentration matrix:
\[ S = \frac{1}{n} (Z' X) (X'Z) \]
where \(Z\) is the matrix of instruments and \(X\) is the matrix of endogenous regressors.
Stock and Yogo provide critical values for different scenarios (bias, size distortion) for a given number of instruments and endogenous regressors, based on the smallest eigenvalue of \(S\). The test compares these eigenvalues against critical values that correspond to thresholds of permissible bias or size distortion in a 2SLS estimator.
- Critical Values and Test Conditions: The critical values derived by Stock and Yogo depend on the level of acceptable bias, the number of endogenous regressors, and the number of instruments. For example, with a 5% maximum acceptable bias, one endogenous variable, and three instruments, the critical value for a sufficient first stage F-statistic is 13.91. Note that this framework requires at least two overidentifying degree of freedom. Stock and Yogo (2002) set the critical values such that the bias is less then 10% (default)
\(H_0:\) Instruments are weak
\(H_1:\) Instruments are not weak
library(cragg)
library(AER) # for dataaset
data("WeakInstrument")
stock_yogo_test(
# control variables
X = ~ Sepal.Length,
# endogeneous variables
D = ~ Sepal.Width,
# instrument variables
Z = ~ Petal.Length + Petal.Width + Species,
size_bias = "bias",
data = iris
)
#> Results of Stock and Yogo test for weak instruments:
#>
#> Null Hypothesis: Instruments are weak
#> Alternative Hypothesis: Instruments are not weak
#>
#> Data: iris
#> Controls: ~Sepal.Length
#> Treatments: ~Sepal.Width
#> Instruments: ~Petal.Length + Petal.Width + Species
#>
#> Alpha: 0.05
#> Acceptable level of bias: 5% relative to OLS.
#> Critical Value: 16.85
#>
#> Cragg-Donald Statistic: 61.30973
#> Df: 14434.6.1.5 Anderson-Rubin Test
The Anderson-Rubin (AR) test addresses the issues of weak instruments by providing a test for the structural parameter (\(\beta\)) that is robust to weak instruments (T. W. Anderson and Rubin 1949). It does not rely on the strength of the instruments to control size, making it a valuable tool for inference when instrument relevance is questionable.
Consider the following linear IV model:
\[ Y = X \beta + u \]
- \(Y\): Dependent variable (\(n \times 1\))
- \(X\): Endogenous regressor (\(n \times k\))
-
\(Z\): Instrument matrix (\(n \times m\)), assumed to satisfy:
- Instrument Exogeneity: \(\mathbb{E}[Z'u] = 0\)
- Instrument Relevance: \(\mathrm{rank}(\mathbb{E}[Z'X]) = k\)
The relevance assumption ensures that \(Z\) contains valid information for predicting \(X\).
Relevance is typically assessed in the first-stage regression:
\[ X = Z \Pi + V \]
If \(Z\) is weakly correlated with \(X\), \(\Pi\) is close to zero, violating the relevance assumption.
The AR test is a Wald-type test for the null hypothesis:
\[ H_0: \beta = \beta_0 \]
It is constructed by examining whether the residuals from imposing \(\beta_0\) are orthogonal to the instruments \(Z\). Specifically:
- Compute the reduced-form residuals under \(H_0\):
\[ r(\beta_0) = Y - X \beta_0 \]
- The AR test statistic is:
\[ AR(\beta_0) = \frac{r(\beta_0)' P_Z r(\beta_0)}{\hat{\sigma}^2} \]
- \(P_Z = Z (Z'Z)^{-1} Z'\) is the projection matrix onto the column space of \(Z\).
- \(\hat{\sigma}^2 = \frac{r(\beta_0)' M_Z r(\beta_0)}{n - m}\) is the residual variance estimator, with \(M_Z = I - P_Z\).
Under \(H_0\), and assuming homoskedasticity, the AR statistic follows an F-distribution:
\[ AR(\beta_0) \sim F(m, n - m) \]
Alternatively, for large \(n\), the AR statistic can be approximated by a chi-squared distribution:
\[ AR(\beta_0) \sim \chi^2_m \]
Interpretation
- If \(AR(\beta_0)\) exceeds the critical value from the \(F\) (or \(\chi^2\)) distribution, we reject \(H_0\).
- The test assesses whether \(r(\beta_0)\) is orthogonal to \(Z\). If not, \(H_0\) is inconsistent with the moment conditions.
The key advantage of the AR test is that its size is correct even when instruments are weak. The AR statistic does not depend on the strength of the instruments (i.e., the magnitude of \(\Pi\)), making it valid under weak identification.
This contrasts with standard 2SLS-based Wald tests, whose distribution depends on the first-stage relevance and can be severely distorted if \(Z\) is weakly correlated with \(X\).
- The relevance assumption is necessary for point identification and consistent estimation in IV.
- If instruments are weak, point estimates of \(\beta\) from 2SLS can be biased.
- The AR test allows for valid hypothesis testing, even if instrument relevance is weak.
However, if instruments are completely irrelevant (i.e., \(Z'X = 0\)), the IV model is unidentified, and the AR test lacks power (i.e., it does not reject \(H_0\) for any \(\beta_0\)).
The AR test can be inverted to form confidence sets for \(\beta\):
- Compute \(AR(\beta)\) for a grid of \(\beta\) values.
- Include all \(\beta\) values for which \(AR(\beta)\) does not reject \(H_0\) at the chosen significance level.
These confidence sets are robust to weak instruments and can be disconnected or unbounded if identification is weak.
set.seed(123)
# Simulate data
n <- 500
Z <- cbind(1, rnorm(n)) # Instrument (include constant)
X <- 0.1 * Z[,2] + rnorm(n) # Weak first-stage relationship
beta_true <- 1
u <- rnorm(n)
Y <- X * beta_true + u
library(ivmodel)
ivmodel(Y = Y, D = X, Z = Z)
#>
#> Call:
#> ivmodel(Y = Y, D = X, Z = Z)
#> sample size: 500
#> _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
#>
#> First Stage Regression Result:
#>
#> F=0.684842, df1=2, df2=497, p-value is 0.50464
#> R-squared=0.002748329, Adjusted R-squared=-0.001264756
#> Residual standard error: 1.01117 on 499 degrees of freedom
#> _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
#>
#> Sargan Test Result:
#>
#> Sargan Test Statistics=0.007046677, df=1, p-value is 0.9331
#> _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
#>
#> Coefficients of k-Class Estimators:
#>
#> k Estimate Std. Error t value Pr(>|t|)
#> OLS 0.00000 1.05559 0.04396 24.015 <2e-16 ***
#> Fuller 0.99800 1.81913 0.80900 2.249 0.0250 *
#> TSLS 1.00000 2.37533 1.40555 1.690 0.0917 .
#> LIML 1.00001 2.38211 1.41382 1.685 0.0926 .
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
#>
#> Alternative tests for the treatment effect under H_0: beta=0.
#>
#> Anderson-Rubin test (under F distribution):
#> F=1.874305, df1=2, df2=497, p-value is 0.15454
#> 95 percent confidence interval:
#> Whole Real Line
#>
#> Conditional Likelihood Ratio test (under Normal approximation):
#> Test Stat=3.741629, p-value is 0.14881
#> 95 percent confidence interval:
#> Whole Real Line34.6.1.6 Stock-Wright Test
While the Anderson-Rubin test offers one solution by constructing test statistics that are valid regardless of instrument strength, another complementary approach is the Stock-Wright test, sometimes referred to as the S-test or Score test. This test belongs to a broader class of conditional likelihood ratio tests proposed by M. J. Moreira (2003) and Stock and Wright (2000), and it plays an important role in constructing weak-instrument robust confidence regions.
The Stock-Wright test exploits the conditional score function of the IV model to test hypotheses about structural parameters, offering robustness under weak identification.
Consider the linear IV model:
\[ Y = X \beta + u \]
- \(Y\): Outcome variable (\(n \times 1\))
- \(X\): Endogenous regressor (\(n \times k\))
- \(Z\): Instrument matrix (\(n \times m\)), where \(m \ge k\)
The exogeneity and relevance assumptions for \(Z\) are:
- \(\mathbb{E}[Z'u] = 0\) (Exogeneity)
- \(\mathrm{rank}(\mathbb{E}[Z'X]) = k\) (Relevance)
Weak instruments imply that the matrix \(\mathbb{E}[Z'X]\) is close to rank-deficient or nearly zero, which can invalidate standard inference.
The goal is to test the null hypothesis:
\[ H_0: \beta = \beta_0 \]
The Stock-Wright test provides a robust way to perform this hypothesis test by constructing a score statistic that is robust to weak instruments.
The score test (or Lagrange Multiplier test) evaluates whether the score (the gradient of the log-likelihood function with respect to \(\beta\)) is close to zero under the null hypothesis.
In the IV context, the conditional score is evaluated from the reduced-form equations. The SW test uses the fact that under \(H_0\), the moment condition:
\[ \mathbb{E}[Z'(Y - X \beta_0)] = 0 \]
should hold. Deviations from this condition can be tested using a score statistic.
The reduced-form equations are:
\[ \begin{aligned} Y &= Z \pi_Y + \epsilon_Y \\ X &= Z \pi_X + \epsilon_X \end{aligned} \]
Under this system:
\(\epsilon_Y\) and \(\epsilon_X\) are jointly normally distributed with covariance matrix \(\Sigma\).
The structural model implies a restriction on \(\pi_Y\): \(\pi_Y = \pi_X \beta\).
The Stock-Wright test statistic is given by:
\[ S(\beta_0) = (Z'(Y - X \beta_0))' \left[ \hat{\Omega}^{-1} \right] (Z'(Y - X \beta_0)) \]
Where:
\(\hat{\Omega}\) is an estimator of the covariance matrix of the moment condition \(Z'u\), often estimated by \(Z'Z\) times an estimator of \(\mathrm{Var}(u)\).
In homoskedastic settings, \(\hat{\Omega} = \hat{\sigma}^2 Z'Z\), with \(\hat{\sigma}^2\) estimated from the residuals under \(H_0\):
\[ \hat{\sigma}^2 = \frac{(Y - X \beta_0)' (Y - X \beta_0)}{n} \]
Under the null hypothesis \(H_0\), the test statistic \(S(\beta_0)\) follows a chi-squared distribution with \(m\) degrees of freedom:
\[ S(\beta_0) \sim \chi^2_m \]
The Stock-Wright test is closely related to the Anderson-Rubin test. However:
- The AR test focuses on the orthogonality of the reduced-form residuals with \(Z\).
- The SW test focuses on the conditional score, derived from the likelihood framework.
- Both are robust to weak instruments, but they have different power properties depending on the data-generating process.
Geometric Intuition
- The SW test can be seen as testing whether the orthogonality condition between \(Z\) and \(u\) holds, using a score function.
- It effectively checks whether the directional derivative of the likelihood (evaluated at \(\beta_0\)) is zero, offering a generalized method of moments interpretation.
The Stock-Wright S-test can be inverted to form confidence regions:
- For a grid of \(\beta\) values, compute \(S(\beta)\).
- The confidence region consists of all \(\beta\) values where \(S(\beta)\) does not reject \(H_0\) at the chosen significance level.
These regions are robust to weak instruments, and can be disconnected or unbounded if the instruments are too weak to deliver informative inference.
set.seed(42)
# Simulate data
n <- 500
Z <- cbind(1, rnorm(n)) # Instrument (include constant)
X <- 0.1 * Z[,2] + rnorm(n) # Weak first-stage relationship
beta_true <- 1
u <- rnorm(n)
Y <- X * beta_true + u
# Null hypothesis to test
beta_0 <- 0
# Residuals under H0
r_beta0 <- Y - X * beta_0
# Estimate variance of residuals under H0
sigma2_hat <- mean(r_beta0^2)
# Compute Omega matrix
Omega_hat <- sigma2_hat * t(Z) %*% Z
# Compute the Stock-Wright S-statistic
S_stat <- t(t(Z) %*% r_beta0) %*% solve(Omega_hat) %*% (t(Z) %*% r_beta0)
# p-value from chi-squared distribution
df <- ncol(Z) # degrees of freedom
p_val <- 1 - pchisq(S_stat, df = df)
# Output
cat("Stock-Wright S-Statistic:", round(S_stat, 4), "\n")
#> Stock-Wright S-Statistic: 5.0957
cat("p-value:", round(p_val, 4), "\n")
#> p-value: 0.078334.6.1.7 Kleibergen-Paap rk Statistic
Traditional diagnostics for instrument relevance, such as:
The first-stage \(F\)-statistic (for single endogenous variables with homoskedastic errors)
The Cragg-Donald statistic (for multiple endogenous regressors under homoskedasticity)
are not valid when errors exhibit heteroskedasticity or non-i.i.d. behavior.
The Kleibergen-Paap (KP) rk statistic addresses these limitations by providing a robust test for underidentification and weak identification in IV models, even in the presence of heteroskedasticity.
Consider the linear IV model:
\[ Y = X \beta + u \]
- \(Y\): Dependent variable (\(n \times 1\))
- \(X\): Matrix of endogenous regressors (\(n \times k\))
- \(Z\): Instrument matrix (\(n \times m\)), with \(m \ge k\)
- \(u\): Structural error term
The moment conditions under exogeneity are:
\[ \mathbb{E}[Z'u] = 0 \]
The relevance assumption requires:
\[ \mathrm{rank}(\mathbb{E}[Z'X]) = k \]
If this condition fails, the model is underidentified, and consistent estimation of \(\beta\) is impossible.
The Kleibergen-Paap rk statistic performs two key functions:
- Test for underidentification (whether the instruments identify the equation)
- Weak identification diagnostics, analogous to the Cragg-Donald statistic, but robust to heteroskedasticity.
Why “rk”?
- “rk” stands for rank—the statistic tests whether the matrix of reduced-form coefficients has full rank, necessary for identification.
The KP rk statistic builds on the generalized method of moments framework and the canonical correlations between \(X\) and \(Z\).
The reduced-form for \(X\) is:
\[ X = Z \Pi + V \]
- \(\Pi\): Matrix of reduced-form coefficients (\(m \times k\))
- \(V\): First-stage residuals (\(n \times k\))
Under the null hypothesis of underidentification, the matrix \(\Pi\) is rank deficient, meaning \(\Pi\) does not have full rank \(k\).
The Kleibergen-Paap rk statistic tests the null hypothesis:
\[ H_0: \mathrm{rank}(\mathbb{E}[Z'X]) < k \]
Against the alternative:
\[ H_A: \mathrm{rank}(\mathbb{E}[Z'X]) = k \]
The Kleibergen-Paap rk statistic is a Lagrange Multiplier test statistic derived from the first-stage canonical correlations between \(X\) and \(Z\), adjusted for heteroskedasticity.
Computation Outline
- Compute first-stage residuals for each endogenous regressor.
- Estimate the covariance matrix of the residuals, allowing for heteroskedasticity.
- Calculate the rank test statistic, which has an asymptotic chi-squared distribution with \(k(m - k)\) degrees of freedom.
Under \(H_0\), the KP rk statistic follows:
\[ KP_{rk} \sim \chi^2_{k(m - k)} \]
Intuition Behind the KP rk Statistic
- The statistic examines whether the moment conditions based on \(Z\) provide enough information to identify \(\beta\).
- If \(Z\) fails to explain sufficient variation in \(X\), the instruments are not relevant, and the model is underidentified.
- The KP rk test is a necessary condition for relevance, though not a sufficient measure of instrument strength.
Practical Usage
- A rejection of \(H_0\) suggests that the instruments are relevant enough for identification.
- A failure to reject \(H_0\) implies underidentification, and the IV estimates are not valid.
While the KP rk statistic tests for underidentification, it does not directly assess weak instruments. However, it is often reported alongside Kleibergen-Paap LM and Wald statistics, which address weak instrument diagnostics in heteroskedastic settings.
Comparison: Kleibergen-Paap rk vs Cragg-Donald Statistic
| Feature | Kleibergen-Paap rk Statistic | Cragg-Donald Statistic |
|---|---|---|
| Robust to Heteroskedasticity | Yes | No |
| Valid Under Non-i.i.d. Errors | Yes | No |
| Underidentification Test | Yes | No (tests weak instruments) |
| Degrees of Freedom | \(k(m - k)\) | Varies (depends on \(k\) and \(m\)) |
| Applicability | Always preferred in practice | Homoskedastic errors only |
# Load necessary packages
library(sandwich) # For robust covariance estimators
library(lmtest) # For testing
library(AER) # For IV estimation (optional)
# Simulate data
set.seed(123)
n <- 500
Z1 <- rnorm(n)
Z2 <- rnorm(n)
Z <- cbind(1, Z1, Z2) # Instruments (include intercept)
# Weak instrument case
X1 <- 0.1 * Z1 + 0.1 * Z2 + rnorm(n)
X <- cbind(X1)
beta_true <- 1
u <- rnorm(n)
Y <- X %*% beta_true + u
# First-stage regression: X ~ Z
first_stage <- lm(X1 ~ Z1 + Z2)
V <- residuals(first_stage) # First-stage residuals
# Calculate robust covariance matrix of residuals
# Note: sandwich package already computes heteroskedasticity-consistent covariances
# Kleibergen-Paap rk test via sandwich estimators (conceptual)
# In practice, Kleibergen-Paap rk statistics are provided by ivreg2 (Stata) or via custom functions
# For illustration, using ivreg and summary statistics
iv_model <- ivreg(Y ~ X1 | Z1 + Z2)
# Kleibergen-Paap rk statistic (reported by summary under diagnostics)
summary(iv_model, diagnostics = TRUE)
#>
#> Call:
#> ivreg(formula = Y ~ X1 | Z1 + Z2)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -3.2259666 -0.6433047 0.0004169 0.8384112 3.4831350
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.05389 0.04810 1.120 0.263
#> X1 1.16437 0.22129 5.262 2.12e-07 ***
#>
#> Diagnostic tests:
#> df1 df2 statistic p-value
#> Weak instruments 2 497 11.793 9.91e-06 ***
#> Wu-Hausman 1 497 2.356 0.12541
#> Sargan 1 NA 6.934 0.00846 **
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 1.066 on 498 degrees of freedom
#> Multiple R-Squared: 0.3593, Adjusted R-squared: 0.358
#> Wald test: 27.69 on 1 and 498 DF, p-value: 2.123e-07
# Interpretation:
# Weak instruments are flagged if the KP rk statistic does not reject underidentification.Interpretation
The Kleibergen-Paap rk statistic is reported alongside LM and Wald weak identification tests.
The p-value of the rk statistic tells us whether the equation is identified.
If the test rejects, we proceed to evaluate weak instrument strength using Wald or LM statistics.
34.6.1.8 Comparison of Weak Instrument Tests
| Test | Description | Use Case | Assumptions |
|---|---|---|---|
| First-Stage F-Statistic | Joint significance of instruments on \(X_2\) | Simple IV models (1 endogenous regressor, 1+ instruments) | i.i.d. errors |
| Cragg-Donald Wald | Wald test for multiple instruments and endogenous variables | Multi-equation IV models | i.i.d. errors |
| Stock-Yogo | Critical values for bias/size distortion | Assess bias and size distortions in 2SLS estimator | i.i.d. errors |
| Anderson-Rubin | Joint significance test in structural equation | Robust to weak instruments; tests hypotheses on \(\beta_2\) | None (valid under weak IV) |
| Kleinbergen-Paap rk | Generalized Cragg-Donald for heteroskedastic/clustered errors | Robust inference when classical assumptions fail; heteroskedastic-consistent inference | Allows heteroskedasticity |
All the mentioned tests (Stock Yogo, Cragg-Donald, Anderson canonical correlation test) assume errors are independently and identically distributed. If this assumption is violated, the Kleinbergen-Paap test is robust against violations of the iid assumption and can be applied even with a single endogenous variable and instrument, provided the model is properly identified (Baum and Lewbel 2019).
34.6.2 Independence (Unconfoundedness)
- \(Z\) is independent of any factors affecting \(Y\), apart from through \(X_2\).
- Formally: \(Z \perp \epsilon\).
This is stronger than exclusion restriction and typically requires randomized assignment of \(Z\) or strong theoretical justification.
34.6.3 Monotonicity Assumption
- Relevant for identifying Local Average Treatment Effects (G. W. Imbens and Angrist 1994)
- Assumes there are no defiers: the instrument \(Z\) does not cause the treatment \(X_2\) to increase for some units while decreasing it for others.
\[ X_2(Z = 1) \ge X_2(Z = 0) \quad \text{for all individuals} \]
- Ensures we are identifying a [Local Average Treatment Effect] (LATE) for the group of compliers—individuals whose treatment status responds to the instrument.
This assumption is particularly important in empirical applications involving binary instruments and heterogeneous treatment effects.
In business settings, instruments often arise from policy changes, eligibility cutoffs, or randomized marketing campaigns. For instance:
- A firm rolls out a new loyalty program (\(Z = 1\)) in selected regions to encourage purchases (\(X_2\)). The monotonicity assumption implies that no customer reduces their purchases because of the program—it only increases or leaves them unchanged.
This assumption rules out defiers—individuals who respond to the instrument in the opposite direction—which would otherwise bias the IV estimate by introducing effects not attributable to compliers. Violations of monotonicity make the IV estimate difficult to interpret, as it may average over both compliers and defiers, yielding a non-causal or ambiguous LATE.
While monotonicity is an assumption about unobserved counterfactuals and thus not directly testable, several empirical strategies can provide suggestive evidence:
- First-Stage Regression
Estimate the impact of the instrument on the treatment. A strong, consistent sign across subgroups supports monotonicity.
set.seed(123)
# Sample size
n <- 1000
# Generate instrument (Z), treatment (D), and outcome (Y)
Z <- rbinom(n, 1, 0.5) # Binary instrument (e.g., policy change)
U <- rnorm(n) # Unobserved confounder
D <- 0.8 * Z + 0.3 * U + rnorm(n) # Treatment variable
Y <- 2 * D + 0.5 * U + rnorm(n) # Outcome variable
# Create a data frame
df <- data.frame(Z, D, Y)
# First-stage regression
first_stage <- lm(D ~ Z, data = df)
summary(first_stage)
#>
#> Call:
#> lm(formula = D ~ Z, data = df)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -3.2277 -0.7054 0.0105 0.7047 3.3846
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.02910 0.04651 0.626 0.532
#> Z 0.74286 0.06623 11.216 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 1.047 on 998 degrees of freedom
#> Multiple R-squared: 0.1119, Adjusted R-squared: 0.111
#> F-statistic: 125.8 on 1 and 998 DF, p-value: < 2.2e-16
# Check F-statistic
fs_f_stat <- summary(first_stage)$fstatistic[1]
fs_f_stat
#> value
#> 125.7911A positive and significant coefficient on \(Z\) supports a monotonic relationship.
If the coefficient is near zero or flips sign in subgroups, this may signal violations.
- Density Plot of First-Stage Residuals
# Extract residuals
residuals_first_stage <- residuals(first_stage)
# Plot density
library(ggplot2)
ggplot(data.frame(residuals = residuals_first_stage),
aes(x = residuals)) +
geom_density(fill = "blue", alpha = 0.5) +
ggtitle("Density of First-Stage Residuals") +
xlab("Residuals from First-Stage Regression") +
ylab("Density") +
causalverse::ama_theme()
A unimodal residual distribution supports monotonicity.
A bimodal or heavily skewed pattern could suggest a mixture of compliers and defiers.
- Subgroup Analysis
Split the sample into subgroups (e.g., by market segment or region) and compare the first-stage coefficients.
# Create two random subgroups
df$subgroup <- ifelse(runif(n) > 0.5, "Group A", "Group B")
# First-stage regression in subgroups
first_stage_A <- lm(D ~ Z, data = df[df$subgroup == "Group A", ])
first_stage_B <- lm(D ~ Z, data = df[df$subgroup == "Group B", ])
# Compare coefficients
coef_A <- coef(first_stage_A)["Z"]
coef_B <- coef(first_stage_B)["Z"]
cat("First-stage coefficient for Group A:", coef_A, "\n")
#> First-stage coefficient for Group A: 0.6645617
cat("First-stage coefficient for Group B:", coef_B, "\n")
#> First-stage coefficient for Group B: 0.8256711If both groups show a coefficient with the same sign, this supports monotonicity.
Opposing signs raise concerns that some individuals may respond against the instrument.
34.6.4 Homogeneous Treatment Effects (Optional)
- Assumes that the causal effect of \(X_2\) on \(Y\) is constant across individuals.
- Without this, IV estimates a local rather than global average treatment effect (LATE vs ATE).
34.6.5 Linearity and Additivity
- The functional form is linear in parameters:
\[ Y = X \beta + \epsilon \]
- No interactions or non-linearities unless explicitly modeled.
- Additivity of the error term \(\epsilon\) implies no heteroskedasticity in classic IV models (though robust standard errors can relax this).
34.6.6 Instrument Exogeneity (Exclusion Restriction)
- \(E[Z \epsilon] = 0\): Instruments must not be correlated with the error term.
- \(Z\) influences \(Y\) only through \(X_2\).
- No omitted variable bias from unobserved confounders correlated with \(Z\).
Key Interpretation:
- \(Z\) has no direct effect on \(Y\).
- Any pathway from \(Z\) to \(Y\) must operate exclusively through \(X_2\).
34.6.7 Exogeneity Assumption
The local average treatment effect (LATE) is defined as:
\[ \text{LATE} = \frac{\text{reduced form}}{\text{first stage}} = \frac{\rho}{\phi} \]
This implies that the reduced form (\(\rho\)) is the product of the first stage (\(\phi\)) and LATE:
\[ \rho = \phi \times \text{LATE} \]
Thus, if the first stage (\(\phi\)) is 0, the reduced form (\(\rho\)) should also be 0.
# Load necessary libraries
library(shiny)
library(AER) # for ivreg
library(ggplot2) # for visualization
library(dplyr) # for data manipulation
# Function to simulate the dataset
simulate_iv_data <- function(n, beta, phi, direct_effect) {
Z <- rnorm(n)
epsilon_x <- rnorm(n)
epsilon_y <- rnorm(n)
X <- phi * Z + epsilon_x
Y <- beta * X + direct_effect * Z + epsilon_y
data <- data.frame(Y = Y, X = X, Z = Z)
return(data)
}
# Function to run the simulations and calculate the effects
run_simulation <- function(n, beta, phi, direct_effect) {
# Simulate the data
simulated_data <- simulate_iv_data(n, beta, phi, direct_effect)
# Estimate first-stage effect (phi)
first_stage <- lm(X ~ Z, data = simulated_data)
phi <- coef(first_stage)["Z"]
phi_ci <- confint(first_stage)["Z", ]
# Estimate reduced-form effect (rho)
reduced_form <- lm(Y ~ Z, data = simulated_data)
rho <- coef(reduced_form)["Z"]
rho_ci <- confint(reduced_form)["Z", ]
# Estimate LATE using IV regression
iv_model <- ivreg(Y ~ X | Z, data = simulated_data)
iv_late <- coef(iv_model)["X"]
iv_late_ci <- confint(iv_model)["X", ]
# Calculate LATE as the ratio of reduced-form and first-stage coefficients
calculated_late <- rho / phi
calculated_late_se <- sqrt(
(rho_ci[2] - rho)^2 / phi^2 + (rho * (phi_ci[2] - phi) / phi^2)^2
)
calculated_late_ci <- c(calculated_late - 1.96 * calculated_late_se,
calculated_late + 1.96 * calculated_late_se)
# Return a list of results
list(phi = phi,
phi_ci = phi_ci,
rho = rho,
rho_ci = rho_ci,
direct_effect = direct_effect,
direct_effect_ci = c(direct_effect, direct_effect), # Placeholder for direct effect CI
iv_late = iv_late,
iv_late_ci = iv_late_ci,
calculated_late = calculated_late,
calculated_late_ci = calculated_late_ci,
true_effect = beta,
true_effect_ci = c(beta, beta)) # Placeholder for true effect CI
}
# Define UI for the sliders
ui <- fluidPage(
titlePanel("IV Model Simulation"),
sidebarLayout(
sidebarPanel(
sliderInput("beta", "True Effect of X on Y (beta):", min = 0, max = 1.0, value = 0.5, step = 0.1),
sliderInput("phi", "First Stage Effect (phi):", min = 0, max = 1.0, value = 0.7, step = 0.1),
sliderInput("direct_effect", "Direct Effect of Z on Y:", min = -0.5, max = 0.5, value = 0, step = 0.1)
),
mainPanel(
plotOutput("dotPlot")
)
)
)
# Define server logic to run the simulation and generate the plot
server <- function(input, output) {
output$dotPlot <- renderPlot({
# Run simulation
results <- run_simulation(n = 1000, beta = input$beta, phi = input$phi, direct_effect = input$direct_effect)
# Prepare data for plotting
plot_data <- data.frame(
Effect = c("First Stage (phi)", "Reduced Form (rho)", "Direct Effect", "LATE (Ratio)", "LATE (IV)", "True Effect"),
Value = c(results$phi, results$rho, results$direct_effect, results$calculated_late, results$iv_late, results$true_effect),
CI_Lower = c(results$phi_ci[1], results$rho_ci[1], results$direct_effect_ci[1], results$calculated_late_ci[1], results$iv_late_ci[1], results$true_effect_ci[1]),
CI_Upper = c(results$phi_ci[2], results$rho_ci[2], results$direct_effect_ci[2], results$calculated_late_ci[2], results$iv_late_ci[2], results$true_effect_ci[2])
)
# Create dot plot with confidence intervals
ggplot(plot_data, aes(x = Effect, y = Value)) +
geom_point(size = 3) +
geom_errorbar(aes(ymin = CI_Lower, ymax = CI_Upper), width = 0.2) +
labs(title = "IV Model Effects",
y = "Coefficient Value") +
coord_cartesian(ylim = c(-1, 1)) + # Limits the y-axis to -1 to 1 but allows CI beyond
theme_minimal() +
theme(axis.text.x = element_text(angle = 45, hjust = 1))
})
}
# Run the application
shinyApp(ui = ui, server = server)A statistically significant reduced form estimate without a corresponding first stage indicates an issue, suggesting an alternative channel linking instruments to outcomes or a direct effect of the IV on the outcome.
- No Direct Effect: When the direct effect is 0 and the first stage is 0, the reduced form is 0.
- Note: Extremely rare cases with multiple additional paths that perfectly cancel each other out can also produce this result, but testing for all possible paths is impractical.
- With Direct Effect: When there is a direct effect of the IV on the outcome, the reduced form can be significantly different from 0, even if the first stage is 0.
- This violates the exogeneity assumption, as the IV should only affect the outcome through the treatment variable.
To test the validity of the exogeneity assumption, we can use a sanity test:
- Identify groups for which the effects of instruments on the treatment variable are small and not significantly different from 0. The reduced form estimate for these groups should also be 0. These “no-first-stage samples” provide evidence of whether the exogeneity assumption is violated.
34.6.7.1 Overid Tests
-
Wald test and Hausman test for exogeneity of \(X\) assuming \(Z\) is exogenous
- People might prefer Wald test over Hausman test.
Sargan (for 2SLS) is a simpler version of Hansen’s J test (for IV-GMM)
Modified J test (i.e., Regularized jacknife IV): can handle weak instruments and small sample size (Carrasco and Doukali 2022) (also proposed a regularized F-test to test relevance assumption that is robust to heteroskedasticity).
New advances: endogeneity robust inference in finite sample and sensitivity analysis of inference (Kiviet 2020)
These tests that can provide evidence fo the validity of the over-identifying restrictions is not sufficient or necessary for the validity of the moment conditions (i.e., this assumption cannot be tested). (Deaton 2010; Parente and Silva 2012)
The over-identifying restriction can still be valid even when the instruments are correlated with the error terms, but then in this case, what you’re estimating is no longer your parameters of interest.
Rejection of the over-identifying restrictions can also be the result of parameter heterogeneity (J. D. Angrist, Graddy, and Imbens 2000)
Why overid tests hold no value/info?
-
Overidentifying restrictions are valid irrespective of the instruments’ validity
- Whenever instruments have the same motivation and are on the same scale, the estimated parameter of interests will be very close (Parente and Silva 2012, 316)
-
Overidentifying restriction are invalid when each instrument is valid
- When the effect of your parameter of interest is heterogeneous (e.g., you have two groups with two different true effects), your first instrument can be correlated with your variable of interest only for the first group and your second interments can be correlated with your variable of interest only for the second group (i.e., each instrument is valid), and if you use each instrument, you can still identify the parameter of interest. However, if you use both of them, what you estimate is a mixture of the two groups. Hence, the overidentifying restriction will be invalid (because no single parameters can make the errors of the model orthogonal to both instruments). The result may seem confusing at first because if each subset of overidentifying restrictions is valid, the full set should also be valid. However, this interpretation is flawed because the residual’s orthogonality to the instruments depends on the chosen set of instruments, and therefore the set of restrictions tested when using two sets of instruments together is not the same as the union of the sets of restrictions tested when using each set of instruments separately (Parente and Silva 2012, 316)
These tests (of overidentifying restrictions) should be used to check whether different instruments identify the same parameters of interest, not to check their validity (J. A. Hausman 1983; Parente and Silva 2012)
34.6.7.1.1 Wald Test
Assuming that \(Z\) is exogenous (a valid instrument), we want to know whether \(X_2\) is exogenous
1st stage:
\[ X_2 = \hat{\alpha} Z + \hat{\epsilon} \]
2nd stage:
\[ Y = \delta_0 X_1 + \delta_1 X_2 + \delta_2 \hat{\epsilon} + u \]
where
- \(\hat{\epsilon}\) is the residuals from the 1st stage
The Wald test of exogeneity assumes
\[ \begin{aligned} H_0: \delta_2 &= 0 \\ H_1: \delta_2 &\neq 0 \end{aligned} \]
If you have more than one endogenous variable with more than one instrument, \(\delta_2\) is a vector of all residuals from all the first-stage equations. And the null hypothesis is that they are jointly equal 0.
If you reject this hypothesis, it means that \(X_2\) is not endogenous. Hence, for this test, we do not want to reject the null hypothesis.
If the test is not sacrificially significant, we might just don’t have enough information to reject the null.
When you have a valid instrument \(Z\), whether \(X_2\) is endogenous or exogenous, your coefficient estimates of \(X_2\) should still be consistent. But if \(X_2\) is exogenous, then 2SLS will be inefficient (i.e., larger standard errors).
Intuition:
\(\hat{\epsilon}\) is the supposed endogenous part of \(X_2\), When we regress \(Y\) on \(\hat{\epsilon}\) and observe that its coefficient is not different from 0. It means that the exogenous part of \(X_2\) can explain well the impact on \(Y\), and there is no endogenous part.
34.6.7.1.2 Hausman’s Test
Similar to Wald Test and identical to Wald Test when we have homoskedasticity (i.e., homogeneity of variances). Because of this assumption, it’s used less often than Wald Test
34.6.7.1.3 Hansen’s J
-
J-test (over-identifying restrictions test): test whether additional instruments are exogenous
- Can only be applied in cases where you have more instruments than endogenous variables
- \(dim(Z) > dim(X_2)\)
- Assume at least one instrument within \(Z\) is exogenous
- Can only be applied in cases where you have more instruments than endogenous variables
Procedure IV-GMM:
- Obtain the residuals of the 2SLS estimation
- Regress the residuals on all instruments and exogenous variables.
- Test the joint hypothesis that all coefficients of the residuals across instruments are 0 (i.e., this is true when instruments are exogenous).
Compute \(J = mF\) where \(m\) is the number of instruments, and \(F\) is your equation \(F\) statistic (can you use
linearHypothesis()again).If your exogeneity assumption is true, then \(J \sim \chi^2_{m-k}\) where \(k\) is the number of endogenous variables.
- If you reject this hypothesis, it can be that
The first sets of instruments are invalid
The second sets of instruments are invalid
Both sets of instruments are invalid
Note: This test is only true when your residuals are homoskedastic.
For a heteroskedasticity-robust \(J\)-statistic, see (Carrasco and Doukali 2022; H. Li et al. 2022)
34.6.7.1.4 Sargan Test
Similar to Hansen’s J, but it assumes homoskedasticity
Have to be careful when sample is not collected exogenously. As such, when you have choice-based sampling design, the sampling weights have to be considered to have consistent estimates. However, even if we apply sampling weights, the tests are not suitable because the iid assumption off errors are already violated. Hence, the test is invalid in this case (Pitt 2011).
If one has heteroskedasticity in its design, the Sargan test is invalid (Pitt 2011})
34.6.7.2 Standard Interpretation of the J-Test for Overidentifying Restrictions Is Misleading
In IV estimation—particularly in overidentified models where the number of instruments \(m\) exceeds the number of endogenous regressors \(k\)—it is standard practice to conduct the J-test (Sargan 1958; L. P. Hansen 1982). Commonly, the J-test (or Sargan-Hansen test) is described as a method to test whether the instruments are valid. But this is misleading. The J-test cannot establish instrument validity merely because it “fails to reject” the null; at best, it can uncover evidence against validity.
What the J-Test Actually Does
Let \(Z\) denote the \(n \times m\) matrix of instruments, and let \(u\) be the structural error term from the IV model. The J-test evaluates the following moment conditions implied by instrument exogeneity:
\[ \begin{aligned} H_0 &: \mathbb{E}[Z'u] = 0 \quad \text{(All moment conditions hold simultaneously)},\\ H_A &: \mathbb{E}[Z'u] \neq 0 \quad \text{(At least one moment condition fails)}. \end{aligned} \]
- Reject \(H_0\): At least one instrument is invalid, or the model is otherwise misspecified.
- Fail to reject \(H_0\): There is no sample evidence that the instruments are invalid—but this does not mean they are necessarily valid.
The J-statistic can be written (in a Generalized Method of Moments context) as:
\[ J = n \hat{g}' W \hat{g}, \]
where \(\hat{g} = \frac{1}{n} \sum_{i=1}^n z_i \hat{u}_i\) is the sample average of instrument–residual covariances (for residuals \(\hat{u}_i\)), and \(W\) is an appropriate weighting matrix (often the inverse of the variance matrix of \(\hat{g}\)).
Under the null, \(J\) is asymptotically \(\chi^2_{m - k}\). A large \(J\) (relative to a \(\chi^2\) critical value) indicates rejection.
Key Insight: Failing to reject the J-test null does not confirm validity. It just means the test did not detect evidence of invalid instruments. If the test has low power (e.g., in small samples or with weak instruments), you may see “no rejection” even when instruments are truly invalid.
Why the “J-Test as a Validity Test” Is the Wrong Way to Think About It
-
The Null Hypothesis Is Almost Always Too Strong
- Economic models are approximations; strict exogeneity rarely holds perfectly.
- Even when instruments are “plausibly” exogenous, the population moment \(\mathbb{E}[Z'u]\) may only approximately hold.
- The J-test requires all instruments to be perfectly valid. Failing to reject \(H_0\) does not prove that they are.
-
Weak Instruments Lead to Weak Power
- The J-test can have low power when instruments are weak.
- You may fail to reject even invalid instruments if the test cannot detect violations.
-
Rejection Does Not Pinpoint Which Instrument Is Invalid
- You only learn that one or more instruments (or the entire model) is problematic; the J-test doesn’t tell you which ones.
-
Model Specification Error Confounds Interpretation
- A J-test rejection can stem from instrument invalidity or from broader model mis-specification (e.g., incorrect functional form).
- The test does not distinguish these sources.
-
Overidentification Itself Does Not Guarantee a Validity Check
- The J-test is only available if \(m > k\). If \(m = k\) (exact identification), no J-test is possible.
- Ironically, exactly-identified models often go “unquestioned” because we cannot run a J-test—yet that does not mean they are more valid.
How to Think About the J-Test Instead
A Diagnostic, Not a Proof
- Rejection: Suggests a problem—invalid instruments or mis-specification.
- No rejection: Implies no detected evidence of invalidity—but not a proof of validity.
Analogy: Not rejecting the J-test null is like a blood test that does not detect a virus. It does not guarantee the patient is healthy; the test may have been insensitive or the sample might have been too small.
Contextual Evaluation Is Key
- Substantive/Theoretical Knowledge: Instrument validity ultimately hinges on whether you can justify \(Z\) being uncorrelated with the error term in theory.
- The J-test is merely complementary, not a substitute for compelling arguments about why instruments are exogenous.
Practical Implications and Recommendations
-
Don’t Rely Solely on the J-Test
- Use it as a screening tool, but always provide theoretical or institutional justification for instrument exogeneity.
-
Assess Instrument Strength Separately
- The J-test says nothing about relevance.
- Weak instruments reduce the power of the J-test.
- Check first-stage \(F\)-statistics or Kleibergen-Paap rk statistics.
-
Sensitivity and Robustness Analysis
- Test different subsets of instruments or alternative specifications.
- Perform leave-one-out analyses to see whether dropping a particular instrument changes conclusions.
-
Use Weak-Instrument-Robust Tests
- Consider Anderson-Rubin, Stock-Wright, or Conditional Likelihood Ratio tests.
- These can remain valid or more robust in the presence of weak instruments or model misspecification.
Summary Table: Common Misinterpretations vs. Reality
| Common Misinterpretation | Correct Understanding |
|---|---|
| “The J-test proves my instruments are valid.” | Failing to reject does not prove validity; it only means no evidence against validity was found. |
| “A high p-value shows strong evidence of validity.” | A high p-value shows no evidence against validity, possibly due to low power or other limitations. |
| “Rejecting the J-test means I know which instrument is bad.” | Rejection only indicates a problem. It doesn’t pinpoint which instrument or whether the issue is broader model misspecification. |
| “The J-test replaces theory in validating instruments.” | The J-test is complementary to theory or institutional knowledge; instrument exogeneity still requires substantive justification. |
# Load packages
library(AER) # Provides ivreg function
# Simulate data for a small demonstration
set.seed(42)
n <- 500
Z1 <- rnorm(n)
Z2 <- rnorm(n)
Z <- cbind(Z1, Z2)
# Construct a (potentially) weak first stage
X <- 0.2 * Z1 + 0.1 * Z2 + rnorm(n)
u <- rnorm(n)
Y <- 1.5 * X + u
# Fit IV (overidentified) using both Z1 and Z2 as instruments
iv_model <- ivreg(Y ~ X | Z1 + Z2)
# Summary with diagnostics, including Sargan-Hansen J-test
summary(iv_model, diagnostics = TRUE)
#>
#> Call:
#> ivreg(formula = Y ~ X | Z1 + Z2)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -2.62393 -0.68911 -0.01314 0.69803 3.53553
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.02941 0.04579 0.642 0.521
#> X 1.47136 0.17654 8.335 7.63e-16 ***
#>
#> Diagnostic tests:
#> df1 df2 statistic p-value
#> Weak instruments 2 497 17.289 5.51e-08 ***
#> Wu-Hausman 1 497 0.003 0.959
#> Sargan 1 NA 0.131 0.717
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 1.005 on 498 degrees of freedom
#> Multiple R-Squared: 0.6794, Adjusted R-squared: 0.6787
#> Wald test: 69.47 on 1 and 498 DF, p-value: 7.628e-16
# Interpretation:
# - If the J-test p-value is large, do NOT conclude "valid instruments."
# - Check the first-stage F-stat or other measures of strength.Interpretation of Output:
A large (non-significant) J-test statistic (with a large p-value) means you do not reject the hypothesis that \(\hat{u} = 0\). It does not prove that all instruments are valid—it only suggests the sample does not provide evidence against validity.
Always pair this with theory-based justifications for \(Z\).
34.6.7.3 J-Test Rejects Even with Valid Instruments (Heterogeneous Treatment Effects)
A more subtle point: The J-test can reject even if all instruments truly are exogenous when the treatment effect is heterogeneous—i.e., each instrument identifies a different local average treatment effect.
The Core Issue: Inconsistent LATEs
The J-test implicitly assumes a single (homogeneous) treatment effect \(\beta\).
If different instruments identify different segments of the population, each instrument can yield a distinct causal effect.
This discrepancy can trigger a J-test rejection, not because the instruments are invalid, but because they don’t agree on a single parameter value.
library(AER)
set.seed(123)
n <- 5000
Z1 <- rbinom(n, 1, 0.5)
Z2 <- rbinom(n, 1, 0.5)
# Assign "complier type" for illustration
# (This is just one way to simulate different subpopulations responding differently.)
complier_type <- ifelse(Z1 == 1 & Z2 == 0, "Z1_only",
ifelse(Z2 == 1 & Z1 == 0, "Z2_only", "Both"))
# True LATEs differ by instrument-induced compliance
beta_Z1 <- 1.0
beta_Z2 <- 2.0
# Generate endogenous X with partial influence from Z1 and Z2
propensity <- 0.2 + 0.5 * Z1 + 0.5 * Z2
X <- rbinom(n, 1, propensity)
u <- rnorm(n)
# Outcome with heterogeneous effects
Y <- ifelse(complier_type == "Z1_only", beta_Z1 * X,
ifelse(complier_type == "Z2_only", beta_Z2 * X, 1.5 * X)) + u
df <- data.frame(Y, X, Z1, Z2)
# IV using Z1 only
iv_Z1 <- ivreg(Y ~ X | Z1, data = df)
summary(iv_Z1)
#>
#> Call:
#> ivreg(formula = Y ~ X | Z1, data = df)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -4.50464 -1.08224 -0.01943 1.08215 4.27937
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 1.1026 0.1101 10.01 < 2e-16 ***
#> X -0.5259 0.1977 -2.66 0.00785 **
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 1.466 on 3802 degrees of freedom
#> Multiple R-Squared: -0.2743, Adjusted R-squared: -0.2746
#> Wald test: 7.076 on 1 and 3802 DF, p-value: 0.007847
# IV using Z2 only
iv_Z2 <- ivreg(Y ~ X | Z2, data = df)
summary(iv_Z2)
#>
#> Call:
#> ivreg(formula = Y ~ X | Z2, data = df)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -4.5025384 -1.1458187 0.0002382 1.1747011 5.0622955
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) -1.2145 0.1279 -9.499 <2e-16 ***
#> X 3.7344 0.2306 16.195 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 1.533 on 3802 degrees of freedom
#> Multiple R-Squared: -0.3948, Adjusted R-squared: -0.3952
#> Wald test: 262.3 on 1 and 3802 DF, p-value: < 2.2e-16
# Overidentified model (Z1 + Z2)
iv_both <- ivreg(Y ~ X | Z1 + Z2, data = df)
summary(iv_both, diagnostics = TRUE)
#>
#> Call:
#> ivreg(formula = Y ~ X | Z1 + Z2, data = df)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -3.46090 -0.71661 -0.01045 0.71687 3.82014
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.02763 0.04423 0.625 0.532
#> X 1.45057 0.07494 19.356 <2e-16 ***
#>
#> Diagnostic tests:
#> df1 df2 statistic p-value
#> Weak instruments 2 3801 510.265 <2e-16 ***
#> Wu-Hausman 1 3801 0.751 0.386
#> Sargan 1 NA 264.175 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 1.059 on 3802 degrees of freedom
#> Multiple R-Squared: 0.3345, Adjusted R-squared: 0.3343
#> Wald test: 374.7 on 1 and 3802 DF, p-value: < 2.2e-16Expected Results
IV via Z1 only should yield an estimate \(\approx 1.0\).
IV via Z2 only should yield \(\approx 2.0\).
IV via Z1 and Z2 together yields a 2SLS estimate that is some weighted average of 1.0 and 2.0.
The J-test often rejects because the data do not support a single \(\beta\) across both instruments.
Key Takeaways
- The J-Test Assumes Homogeneity
- If treatment effects vary with the subpopulation that each instrument induces into treatment, the J-test can reject even when all instruments are exogenous.
- A Rejection May Signal Heterogeneity, Not Invalidity
- The test cannot distinguish invalid exogeneity from different underlying causal parameters.
- Practical Implications
Be aware of the [Local Average Treatment Effect] interpretation of your instruments.
If multiple instruments target different “complier” groups, the standard J-test lumps them into one homogenous \(\beta\).
Consider reporting separate IV estimates or using methods that explicitly account for treatment-effect heterogeneity (e.g., Marginal Treatment Effects or other advanced frameworks).
34.7 Cautions in IV
34.7.1 Negative \(R^2\) in IV
In IV estimation, particularly 2SLS and 3SLS, it is common and not problematic to encounter negative \(R^2\) values in the second stage regression. Unlike Ordinary Least Squares, where \(R^2\) is often used to assess the fit of the model, in IV regression the primary concern is consistency and unbiased estimation of the coefficients of interest, not the goodness-of-fit.
What Should You Look At Instead of \(R^2\) in IV?
- Instrument Relevance (First-stage \(F\)-statistics, Partial \(R^2\))
- Weak Instrument Tests (Kleibergen-Paap, Anderson-Rubin tests)
- Validity of Instruments (Overidentification tests like Sargan/Hansen J-test)
- Endogeneity Tests (Durbin-Wu-Hausman test for endogeneity)
- Confidence Intervals and Standard Errors, focusing on inference for \(\hat{\beta}\).
Geometric Intuition
- In OLS, the fitted values \(\hat{y}\) are the orthogonal projection of \(y\) onto the column space of \(X\).
- In 2SLS, \(\hat{y}\) is the projection onto the space spanned by \(Z\), not \(X\).
- As a result, the angle between \(y\) and \(\hat{y}\) may not minimize the residual variance, and RSS can be larger than in OLS.
Recall the formula for the coefficient of determination (\(R^2\)) in a regression model:
\[ R^2 = 1 - \frac{RSS}{TSS} = \frac{MSS}{TSS} \]
Where:
- \(TSS\) is the Total Sum of Squares: \[ TSS = \sum_{i=1}^n (y_i - \bar{y})^2 \]
- \(MSS\) is the Model Sum of Squares: \[ MSS = \sum_{i=1}^n (\hat{y}_i - \bar{y})^2 \]
- \(RSS\) is the Residual Sum of Squares: \[ RSS = \sum_{i=1}^n (y_i - \hat{y}_i)^2 \]
In OLS, the \(R^2\) measures the proportion of variance in \(Y\) that is explained by the regressors \(X\).
Key Properties in OLS:
- \(R^2 \in [0, 1]\)
- Adding more regressors (even irrelevant ones) never decreases \(R^2\).
- \(R^2\) measures in-sample goodness-of-fit, not causal interpretation.
34.7.1.1 Why Does \(R^2\) Lose Its Meaning in IV Regression?
In IV regression, the second stage regression replaces the endogenous variable \(X_2\) with its predicted values from the first stage:
Stage 1:
\[ X_2 = Z \pi + v \]
Stage 2:
\[ Y = X_1 \beta_1 + \hat{X}_2 \beta_2 + \epsilon \]
- \(\hat{X}_2\) is not the observed \(X_2\), but a proxy constructed from \(Z\).
- \(\hat{X}_2\) isolates the exogenous variation in \(X_2\) that is independent of \(\epsilon\).
- This reduces bias, but comes at a cost:
- The variation in \(\hat{X}_2\) is typically less than that in \(X_2\).
- The predicted values \(\hat{y}_i\) from the second stage are not necessarily close to \(y_i\).
34.7.1.2 Why \(R^2\) Can Be Negative:
- \(R^2\) is calculated using: \[ R^2 = 1 - \frac{RSS}{TSS} \] But in IV:
- The predicted values of \(Y\) are not chosen to minimize RSS, because IV is not minimizing the residuals in the second stage.
- Unlike OLS, 2SLS chooses \(\hat{\beta}\) to satisfy moment conditions rather than minimizing the sum of squared errors.
It is possible (and common in IV) for the residual sum of squares to be greater than the total sum of squares: \[ RSS > TSS \] Which makes: \[ R^2 = 1 - \frac{RSS}{TSS} < 0 \]
-
This happens because:
- The predicted values \(\hat{y}_i\) in IV are not optimized to fit the observed \(y_i\).
- The residuals can be larger, because IV focuses on identifying causal effects, not prediction.
For example, assume we have:
\(TSS = 100\)
\(RSS = 120\)
Then: \[ R^2 = 1 - \frac{120}{100} = -0.20 \]
This happens because the IV procedure does not minimize RSS. It prioritizes solving the endogeneity problem over explaining the variance in \(Y\).
34.7.1.3 Why We Don’t Care About \(R^2\) in IV
- IV Estimates Focus on Consistency, Not Prediction
- The goal of IV is to obtain a consistent estimate of \(\beta_2\).
- IV sacrifices fit (higher variance in \(\hat{y}_i\)) to remove endogeneity bias.
- \(R^2\) Does Not Reflect the Quality of an IV Estimator
- A high \(R^2\) in IV may be misleading (for instance, when instruments are weak or invalid).
- A negative \(R^2\) does not imply a bad IV estimator if the assumptions of instrument validity are met.
- IV Regression Is About Identification, Not In-Sample Fit
- IV relies on relevance and exogeneity of instruments, not residual minimization.
34.7.1.4 Technical Details on \(R^2\)
In OLS: \[ \hat{\beta}^{OLS} = (X'X)^{-1} X'Y \] Minimizes: \[ RSS = (Y - X \hat{\beta}^{OLS})'(Y - X \hat{\beta}^{OLS}) \]
In IV: \[ \hat{\beta}^{IV} = (X'P_Z X)^{-1} X'P_Z Y \]
where:
\(P_Z = Z (Z'Z)^{-1} Z'\) is the projection matrix onto \(Z\).
The IV estimator solves: \[ Z'(Y - X\hat{\beta}) = 0 \]
No guarantee that this minimizes RSS.
Residuals:
\[ e^{IV} = Y - X \hat{\beta}^{IV} \]
The norm of \(e^{IV}\) is typically larger than in OLS because IV uses fewer effective degrees of freedom (constrained variation via \(Z\)).
A Note on \(R^2\) in 3SLS and GMM
- In 3SLS or GMM IV, \(R^2\) can be similarly misleading.
- These methods often operate under moment conditions or system estimation, not residual minimization.
34.7.2 Many-Instruments Bias
While IV is powerful, it is also delicate. One critical issue that arises is the many-instruments problem, also known as many-IV bias.
Consider the structural model:
\(y_i = \beta x_i + u_i\)
where \(x_i\) is endogenous: \(\mathbb{E}[x_i u_i] \neq 0\). To address this, we introduce instruments \(z_i\) such that:
- Relevance: \(\mathbb{E}[z_i x_i] \neq 0\)
- Exogeneity: \(\mathbb{E}[z_i u_i] = 0\)
The standard 2SLS estimator is given by:
\(\hat{\beta}_{2SLS} = (X'P_ZX)^{-1} X'P_Zy\)
where \(P_Z = Z(Z'Z)^{-1}Z'\) is the projection matrix onto the column space of \(Z\).
The many-IV problem arises when the number of instruments \(L\) is large relative to the number of observations \(n\). In particular, the issue becomes severe as \(L/n \to \alpha > 0\), leading to several problems:
- Bias Toward OLS: The 2SLS estimator becomes increasingly biased toward the OLS estimator.
- Overfitting: The first-stage regression overfits the endogenous variable, capturing noise rather than true variation.
- Inflated Variance: The second-stage estimates become imprecise, leading to misleading inference.
Traditional IV asymptotics assume \(L\) is fixed as \(n \to \infty\). Bekker (1994) proposed an alternative framework where:
\(L/n \to \alpha \in (0, \infty) \quad \text{as } n \to \infty\)
Under Bekker asymptotics:
- 2SLS is biased and inconsistent unless the instruments are very strong.
- The bias grows with \(\alpha\), approaching that of OLS.
This formalized the intuition that adding more instruments—especially weak ones—does not help, and can actually harm estimation.
34.7.2.1 Sources of Many-IV Bias
Many instruments are individually weak (i.e., contribute little to explaining \(x\)), and collectively, they inflate the projection without improving identification.
- Overfitting the First Stage
With too many instruments, the first-stage regression captures random noise, leading to poor out-of-sample performance and contamination of the second stage.
- Endogeneity Leakage
Overfit first-stage predictions may reintroduce endogeneity due to incidental correlation with the structural error term.
34.7.2.2 Diagnostic Tools
- First-Stage F-Statistic
A weak instrument test: rule of thumb is \(F > 10\) for a single instrument; more stringent thresholds apply for many instruments.
- Overidentification Tests
- Sargan Test: Assumes homoskedastic errors
- Hansen’s J-Test: Robust to heteroskedasticity
- Eigenvalue Diagnostics
- Kleibergen-Paap rk statistic (generalized for clustered or heteroskedastic settings)
34.7.2.3 Remedies and Alternatives
- Instrument Selection
- Lasso IV / Post-Double Selection: Use regularization to select valid instruments.
- Factor-Based Methods: Project instruments onto principal components.
- Shrinkage Estimators
- Limited Information Maximum Likelihood (LIML): More robust to many-IV bias.
- Jackknife IV Estimator (JIVE): Adjusts for the overfitting bias in the first stage.
- Grouped or Aggregated Instruments
- Collapse multiple instruments into a smaller number of aggregated measures.
34.7.2.4 Practical Guidelines
- Avoid Including All Possible Instruments: Parsimony matters more than volume.
- Always Check First-Stage Strength: Even if \(R^2\) is high, individual instrument strength matters.
- Report Robustness with Alternative Estimators: LIML or JIVE can serve as robustness checks.
- Test for Overidentification: But interpret results cautiously when \(L\) is large.
34.7.3 Heterogeneous Effects in IV Estimation
34.7.3.1 Constant vs. Heterogeneous Treatment Effects
The standard instrumental variables framework assumes that the causal effect of an endogenous regressor \(D_i\) on an outcome \(Y_i\) is constant across individuals, i.e.:
\[ Y_i = \beta_0 + \beta_1 D_i + u_i \]
This implies homogeneous treatment effects, where \(\beta_1\) is a structural parameter that applies uniformly to all individuals \(i\) in the population. We refer to this as the homogeneous treatment effects model, and it underlies the traditional IV assumptions:
Linearity with a constant effect \(\beta_1\).
Instrument relevance: \(\mathrm{Cov}(Z_i, D_i) \ne 0\).
Instrument exogeneity: \(\mathrm{Cov}(Z_i, u_i) = 0\).
Under these assumptions, the IV estimator \(\hat{\beta}_1^{IV}\) consistently estimates the causal effect \(\beta_1\).
34.7.3.2 Heterogeneous Treatment Effects and the Problem for IV
In practice, treatment effects often vary across individuals. That is, the effect of \(D_i\) on \(Y_i\) depends on the individual’s characteristics or other unobserved factors:
\[ Y_i = \beta_{1i} D_i + u_i \]
Here, \(\beta_{1i}\) represents the individual-specific causal effect, and the population Average Treatment Effect is:
\[ ATE = \mathbb{E}[\beta_{1i}] \]
In the presence of treatment effect heterogeneity, the IV estimator \(\hat{\beta}_1^{IV}\) does not, in general, estimate the ATE. Instead, it estimates a weighted average of the heterogeneous treatment effects, with weights determined by the instrumental variation in the data.
This distinction is critical:
OLS estimates a weighted average treatment effect, with weights depending on the variance of \(D_i\).
IV estimates a [Local Average Treatment Effect] (LATE), depending on the instrument \(Z_i\).
When there is one endogenous regressor \(D_i\) and one instrument \(Z_i\), both binary variables, we can interpret the IV estimator as the [Local Average Treatment Effect] under specific assumptions. The setup is:
\[ Y_i = \beta_0 + \beta_{1i} D_i + u_i \]
- \(D_i \in \{0, 1\}\): The treatment indicator.
- \(Z_i \in \{0, 1\}\): The binary instrument.
Assumptions for the LATE Interpretation
\[ Z_i \perp (u_i, v_i) \] - The instrument is as good as randomly assigned, and is independent of both the structural error term \(u_i\) and the unobserved determinants \(v_i\) that affect treatment selection.
\[ \mathbb{P}(D_i = 1 | Z_i = 1) \ne \mathbb{P}(D_i = 1 | Z_i = 0) \] - The instrument must affect the likelihood of receiving treatment \(D_i\).
\[ D_i(1) \ge D_i(0) \quad \forall i \]
There are no defiers: no individual who takes the treatment when \(Z_i = 0\) but does not take it when \(Z_i = 1\).
Monotonicity is not testable, but must be defended on theoretical grounds.
Under these assumptions, \(\hat{\beta}_1^{IV}\) estimates the [Local Average Treatment Effect]:
\[ LATE = \mathbb{E}[\beta_{1i} | \text{Compliers}] \]
- Compliers are individuals who receive the treatment when \(Z_i = 1\), but not when \(Z_i = 0\).
- Local refers to the fact that the estimate pertains to this specific subpopulation of compliers.
Implications:
- The LATE is not the ATE, unless treatment effects are homogeneous, or the complier subpopulation is representative of the entire population.
- Different instruments define different complier groups, leading to different LATEs.
34.7.3.3 Multiple Instruments and Multiple LATEs
When we have multiple instruments \(Z_i^{(1)}, Z_i^{(2)}, \dots, Z_i^{(m)}\), each can induce different complier groups:
Each instrument has its own LATE, corresponding to its own group of compliers.
If heterogeneous treatment effects exist, these LATEs may differ.
In an overidentified model, where \(m > k\), the 2SLS estimator imposes the assumption that all instruments identify the same causal effect \(\beta_1\). This leads to the moment conditions:
\[ \mathbb{E}[Z_i^{(j)}(Y_i - D_i \beta_1)] = 0 \quad \forall j = 1, \dots, m \]
If instruments identify different LATEs:
These moment conditions can be inconsistent with one another.
The Sargan-Hansen J-test may reject, even though each instrument is valid (i.e., exogenous and relevant).
Key Insight: The J-test rejects because the homogeneity assumption is violated—not because instruments are invalid in the exogeneity sense.
34.7.3.4 Illustration: Multiple Instruments, Different LATEs
Consider the following example:
\(Z_i^{(1)}\) identifies a LATE of 1.0.
\(Z_i^{(2)}\) identifies a LATE of 2.0.
-
If both instruments are included in an overidentified IV model, the 2SLS estimator tries to reconcile these LATEs as if they were identifying the same \(\beta_1\), leading to:
An average of these LATEs.
A possible rejection of the overidentification restrictions via the J-test.
This scenario is common in:
Labor economics (e.g., different instruments for education identify different populations).
Marketing and pricing experiments (e.g., different price instruments impact different customer segments).
34.7.3.5 Practical Implications for Empirical Research
- Be Clear About Whose Effect You’re Estimating
- Different instruments often imply different complier groups.
- Understanding who the compliers are is essential for policy implications.
- Interpret the J-Test Carefully
- A rejection may indicate treatment effect heterogeneity, not necessarily instrument invalidity.
- Supplement the J-test with:
- Subgroup analysis.
- Sensitivity analysis.
- Local Instrumental Variable or Marginal Treatment Effects frameworks.
- Use Structural Models When Needed
- If you need an ATE, consider parametric or semi-parametric structural models that explicitly model heterogeneity.
- Don’t Assume LATE = ATE
- Be cautious in generalizing LATE estimates beyond the complier subpopulation.
34.7.3.6 Beyond LATE
The presence of heterogeneous treatment effects (\(\beta_{1i}\) varying across individuals) raises a fundamental challenge for causal inference using IV methods. As we have seen, the traditional IV estimator identifies the [Local Average Treatment Effect] (LATE) under certain assumptions. However, this approach implicitly adopts a reverse engineering strategy: it uses classical linear IV estimators designed under homogeneity, acknowledges their likely misspecification in the presence of unobserved heterogeneity, and interprets the resulting estimate in terms of a LATE.
This strategy has been highly influential and remains central to empirical work. Nevertheless, it comes with limitations:
- The interpretation depends critically on the specific instrument used (i.e., the definition of the complier group).
- It cannot recover the Average Treatment Effect (ATE) or other policy-relevant parameters unless strong additional assumptions hold.
34.7.3.7 Forward Engineering: The Marginal Treatment Effect
In contrast, recent work—including that of Mogstad and Torgovitsky (2024) —emphasizes a forward engineering approach. Rather than adapting estimators designed under homogeneity, this strategy builds models and estimators that explicitly allow for unobserved heterogeneity in treatment effects from the outset.
A key framework in this approach is the Marginal Treatment Effect (MTE), originally developed in the context of selection models (Gronau 1974; J. J. Heckman 1979). The idea is to model the treatment decision as the result of a latent index:
\[ D_i = \mathbb{1}[v_i \leq Z_i'\pi + \eta_i] \]
and to let the treatment effect vary with unobserved selection variables. The MTE is then defined as:
\[ \text{MTE}(u) = \mathbb{E}[Y_i(1) - Y_i(0) | U_i = u] \]
where \(U_i\) is the latent variable governing treatment selection. This function traces out how the treatment effect varies across individuals with different propensities to receive treatment, and it underlies other average effects such as:
- ATE: \(\int_0^1 \text{MTE}(u) du\)
- LATE: average of MTE over complier margin
- TT and TUT: other weighted averages of MTE
Comparison of IV, LATE, and MTE Approaches
| Feature | Traditional IV (LATE) | MTE / Selection Models |
|---|---|---|
| Assumes constant effects | Implicitly violated | Explicitly allows heterogeneity |
| Interpretation | LATE for compliers | MTE curve + all average treatment effects |
| Data requirements | Instrument + outcome | Richer variation in instrument (e.g., continuous) |
| Estimation complexity | Low (2SLS) | Higher (requires modeling selection) |
The MTE framework also connects to:
- Control function methods: which account for selection via inclusion of latent variables (e.g., residuals) in outcome equations.
- Partial identification / bounding methods: which avoid strong parametric assumptions and seek informative bounds on treatment effects.
These newer strategies reflect a shift in modern econometrics: away from treating unobserved heterogeneity as a nuisance, and toward modeling it directly for richer causal inference.
Understanding these two strategies helps practitioners choose appropriate methods based on:
- Their identifying assumptions.
- The richness of their instruments.
- Their target estimand (e.g., ATE, LATE, MTE).
- Their willingness to model the selection process.
Researchers should be cautious in interpreting IV estimates as general causal effects, especially when heterogeneous treatment effects are likely and the choice of instrument strongly influences the complier population.
34.7.4 Zero-Valued Outcomes
For outcomes that take zero values, log transformations can introduce interpretation issues. Specifically, the coefficient on a log-transformed outcome does not directly represent a percentage change (J. Chen and Roth 2024). We have to distinguish the treatment effect on the intensive (outcome: 10 to 11) vs. extensive margins (outcome: 0 to 1), and we can’t readily interpret the treatment coefficient of log-transformed outcome regression as percentage change. In such cases, researchers use alternative methods:
34.7.4.1 Proportional LATE Estimation
When dealing with zero-valued outcomes, direct log transformations can lead to interpretation issues. To obtain an interpretable percentage change in the outcome due to treatment among compliers, we estimate the proportional Local Average Treatment Effect (LATE), denoted as \(\theta_{ATE\%}\).
Steps to Estimate Proportional LATE:
-
Estimate LATE using 2SLS:
We first estimate the treatment effect using a standard Two-Stage Least Squares regression: \[ Y_i = \beta D_i + X_i + \epsilon_i, \] where:
- \(D_i\) is the endogenous treatment variable.
- \(X_i\) includes any exogenous controls.
- \(\beta\) represents the LATE in levels for the mean of the control group’s compliers.
-
Estimate the control complier mean (\(\beta_{cc}\)):
Using the same 2SLS setup, we estimate the control mean for compliers by transforming the outcome variable (Abadie, Angrist, and Imbens 2002): \[ Y_i^{CC} = -(D_i - 1) Y_i. \] The estimated coefficient from this regression, \(\beta_{cc}\), captures the mean outcome for compliers in the control group.
-
Compute the proportional LATE:
The estimated proportional LATE is given by: \[ \theta_{ATE\%} = \frac{\hat{\beta}}{\hat{\beta}_{cc}}, \] which provides a direct percentage change interpretation for the outcome among compliers induced by the instrument.
-
Obtain standard errors via non-parametric bootstrap:
Since \(\theta_{ATE\%}\) is a ratio of estimated coefficients, standard errors are best obtained using non-parametric bootstrap methods.
-
Special case: Binary instrument
If the instrument is binary, \(\theta_{ATE\%}\) for the intensive margin of compliers can be directly estimated using Poisson IV regression (
ivpoissonin Stata).
34.7.4.2 Bounds on Intensive-Margin Effects
Lee (2009) proposed a bounding approach for intensive-margin effects, assuming that compliers always have positive outcomes regardless of treatment (i.e., intensive-margin effect). These bounds help estimate treatment effects without relying on log transformations. However, this requires a monotonicity assumption for compliers where they should still have positive outcome regardless of treatment status.
34.8 Types of IV
34.8.1 Treatment Intensity
Two-Stage Least Squares is a powerful method for estimating the average causal effect when treatment intensity varies across units. Rather than simple binary treatment (treated vs. untreated), many empirical applications involve treatments that can take on a range of values. TSLS can identify causal effects in these settings, capturing “a weighted average of per-unit treatment effects along the length of a causal response function” (J. D. Angrist and Imbens 1995, 431).
Common examples of treatment intensity include:
- Drug dosage (e.g., milligrams administered)
- Hours of exam preparation on test performance (Powers and Swinton 1984)
- Cigarette consumption (e.g., packs per day) on infant birth weights (Permutt and Hebel 1989)
- Years of education and their effect on earnings
- Class size and its impact on student test scores (J. D. Angrist and Lavy 1999)
- Sibship size and later-life earnings (J. Angrist, Lavy, and Schlosser 2010)
- Social media adoption intensity (e.g., time spent, number of platforms)
The average causal effect here refers to the conditional expectation of the difference in outcomes between the treated unit (at a given treatment intensity) and what would have happened in the counterfactual scenario (at a different treatment intensity). Importantly:
- Linearity is not required in the relationships between the dependent variable, treatment intensities, and instruments. TSLS can accommodate nonlinear causal response functions, provided the assumptions of the method hold.
34.8.1.1 Example: Schooling and Earnings
In their seminal paper, J. D. Angrist and Imbens (1995) estimate the causal effect of years of schooling on earnings, using quarter of birth as an instrumental variable. The intuition is that individuals born in different quarters are subject to different compulsory schooling laws, which affect educational attainment but are plausibly unrelated to unobserved ability or motivation (the typical omitted variables in this context).
The structural outcome equation is:
\[ Y = \gamma_0 + \gamma_1 X_1 + \rho S + \varepsilon \]
where:
- \(Y\) is the log of earnings (the dependent variable)
- \(S\) is years of schooling (the endogenous regressor)
- \(X_1\) is a vector (or matrix) of exogenous covariates (e.g., demographic characteristics)
- \(\rho\) is the causal return to schooling we wish to estimate
- \(\varepsilon\) is the error term, capturing unobserved factors
Because schooling \(S\) may be endogenous (e.g., correlated with \(\varepsilon\)), we model its first-stage relationship with the exogenous variables and instruments:
\[ S = \delta_0 + X_1 \delta_1 + X_2 \delta_2 + \eta \]
where:
- \(X_2\) represents the instrumental variables (e.g., quarter of birth)
- \(\delta_2\) is the coefficient on the instrument
- \(\eta\) is the first-stage error term
The Two-Stage Procedure
-
First Stage Regression
Regress \(S\) on \(X_1\) and \(X_2\) to obtain the predicted (fitted) values \(\hat{S}\).
\[ \hat{S} = \widehat{\delta_0} + X_1 \widehat{\delta_1} + X_2 \widehat{\delta_2} \]
-
Second Stage Regression
Replace \(S\) with \(\hat{S}\) in the structural equation and estimate:
\[ Y = \gamma_0 + \gamma_1 X_1 + \rho \hat{S} + \nu \]
where \(\nu\) is the new error term (different from \(\varepsilon\) because \(\hat{S}\) is constructed to be exogenous).
Under the standard IV assumptions, \(\rho\) is a consistent estimator of the causal effect of schooling on earnings.
34.8.1.2 Causal Interpretation of \(\rho\)
For \(\rho\) to have a valid causal interpretation, two key assumptions are essential:
- SUTVA (Stable Unit Treatment Value Assumption)
- The potential outcomes of each individual are not affected by the treatment assignments of other units.
- There are no hidden variations of the treatment; “one year of schooling” means the same treatment type across individuals.
- While important, SUTVA is often assumed without extensive defense in empirical work, though violations (e.g., spillovers in education settings) should be acknowledged when plausible.
- [Local Average Treatment Effect] (LATE)
- TSLS identifies a weighted average of marginal effects at the points where the instrument induces variation in treatment intensity.
- Formally, \(\rho\) converges in probability to a weighted average of causal increments:
\[ \text{plim } \hat{\rho} = \sum_j w_j \cdot E[Y_j - Y_{j-1} \mid \text{Compliers at level } j] \]
where \(w_j\) are weights determined by the distribution of the instrument and treatment intensity.
- This LATE interpretation means that TSLS estimates apply to compliers whose treatment intensity changes in response to the instrument. If there is heterogeneity in treatment effects across units, the interpretation of \(\rho\) becomes instrument-dependent and may not generalize to the entire population.
34.8.2 Decision-Maker IV
Examiner designs, judge IV designs, and leniency IV refer to a family of instrumental variable strategies that exploit quasi-random assignment of decision-makers (such as judges or examiners) to observational units. These designs are used to identify causal effects in settings where controlled experiments are not feasible.
Examiner/judge IV design is an approach where the instrument is the identity or behavior of an assigned decision-maker (an “examiner” or a judge). The classic setup arises in courts: cases are typically assigned to judges in a manner that is as good as random (often conditional on timing or location), and different judges have systematically different propensities to rule harshly or leniently. This means that, purely by the luck of the draw, otherwise-similar individuals may receive different treatments (e.g. a longer vs. shorter sentence) depending on which judge they happen to get. In such a design, the judge assignment (or a function of it) serves as an instrumental variable for the treatment of interest (like sentence length). The key insight is that who the examiner/judge is can be treated as an exogenous shock that influences the treatment but is (ideally) unrelated to the person’s own characteristics.
The term judge IV design specifically refers to using judges in legal settings as instruments. This approach rose to prominence through studies of the criminal justice system; a well-known early example is Kling (2006), who used randomly assigned judges to instrument for incarceration length when studying its effect on later earnings. More generally, the literature often calls this the “judge leniency” design, because it leverages differences in judges’ leniency/harshness. Importantly, the same idea extends beyond literal judges. Examiners in various administrative or medical contexts can play an analogous role. For instance, bureaucrats evaluating benefit claims, patent examiners reviewing applications, or physicians making discretionary treatment decisions can all act like “judges” whose assignment is as-good-as-random and whose leniency varies. In these non-court contexts, researchers sometimes use the term examiner design as a more general label, but it is essentially the same IV strategy. In summary, whether we say examiner design, judge IV, or judge leniency IV, we are usually referring to the same identification strategy – using the quasi-random assignment of a decision-maker with varying tendencies as an instrument.
How the design is structured: In practice, one can implement this IV in a couple of ways. One method is to include dummy variables for each judge/examiner as instruments (since each judge is a distinct source of variation). Another common approach is to construct a leniency measure for each decision-maker – for example, the judge’s historical rate of granting the treatment – and use that as a single continuous instrument. The latter approach (using a summary measure of leniency) is popular because it reduces dimensionality and mitigates weak-instrument concerns when there are many judges. For instance, instead of having 50 separate judge dummies, one can calculate each judge’s leave-one-out approval or sentencing rate and use that number as the instrument. This “leave-one-out” or jackknife approach ensures the measure for each judge is calculated excluding the case in question (avoiding mechanical endogeneity). Overall, the examiner/judge IV design turns the naturally occurring randomness in examiner assignment into a source of exogenous variation: who you were randomly assigned to becomes the instrument for the treatment you received.
34.8.2.1 Achieving Identification with a Leniency IV
The examiner/judge design is a powerful way to achieve identification in observational data. It rests on the core requirements for a valid instrumental variable:
-
Quasi-Random Assignment (Exogeneity): Because examiners or judges are assigned to cases essentially at random (often by rotation, scheduling, or lottery), the particular decision-maker an individual gets is independent of that individual’s characteristics. This approximates the randomness of an experiment. As long as assignment is truly random (or as-good-as-random after conditioning on any known factors like time or location), the examiner identity is uncorrelated with unobserved confounders. In other words, which judge you draw should have no direct bearing on your outcome except through the judge’s decision. This satisfies the exogeneity condition for an IV.
Discretion Over a Binary Treatment: Each decision maker has discretionary authority over a treatment variable \(D_i\), typically binary (e.g., pretrial release vs. detention).
Heterogeneity in Behavior: Decision makers differ systematically in their propensity to assign treatment, allowing us to use these differences as instrumental variation.
Instrument Relevance: Different examiners have different propensities to deliver the treatment. Some judges are more severe (more likely to incarcerate or give long sentences), while others are more lenient; some doctors are more likely to prescribe an intensive treatment, etc. This translates into substantial variation in the probability of treatment based solely on who the case was assigned to. For example, in the patent context, being assigned a lenient patent examiner vs. a strict one can significantly change the probability of a patent grant (Farre-Mensa, Hegde, and Ljungqvist 2020).
Exclusion Restriction: The IV assumption is that the assigned examiner affects the outcome only through the treatment itself. In a judge design, this means the “type of judge you are assigned” should impact the defendant’s future outcomes solely via the judge’s decision (e.g. incarceration or release), not through any other channel. For instance, a harsh judge might send you to prison; a lenient judge might not – that difference can affect your future, but we assume that it’s only the incarceration that matters for your future outcome, not any direct effect of interacting with a harsh vs. nice judge per se. This exclusion restriction is more plausible when the decision-maker has no direct interaction with the individual beyond making the decision. Researchers take care to argue that conditional on the controls and the treatment itself, the identity of the examiner has no independent effect on outcomes. If these conditions (relevance and exogeneity/exclusion) hold, then the variation in treatment induced by examiner assignment can be used to consistently estimate the causal effect of the treatment.
By meeting these conditions, examiner/judge IV designs create a natural experiment. Essentially, they compare outcomes between individuals who, by random luck, received different treatment assignments (e.g. one was incarcerated, another not) due to differing examiner leniency, despite those individuals being comparable in expectation. This helps isolate the causal impact of the treatment from confounding factors. Notably, the estimates from such designs often correspond to a local average treatment effect (LATE) for those cases whose treatment status is swayed by the examiner’s leniency – for example, the “marginal” defendants who would be incarcerated by a strict judge but released by a lenient judge. In sum, these designs allow researchers to mimic a randomized experiment within observational data by leveraging institutional randomness (who gets assigned to whom) as an instrument.
34.8.2.2 Leniency IV: Clarifying the Terminology
The term leniency IV refers to this same instrumental variable strategy, emphasizing the role of the examiner’s leniency (or strictness). In many studies, the instrument is literally a measure of how lenient the assigned judge or examiner tends to be. For example, in a Social Security Disability study, researchers “exploit variation in examiners’ allowance rates as an instrument for benefit receipt.” (Maestas, Mullen, and Strand 2013). Here, an examiner’s allowance rate (the fraction of cases they approve) is a direct quantification of their leniency, and this serves as the instrumental variable. Similarly, one can define a judge’s leniency as the percentage of past defendants that judge jailed or the average sentence length they give, and use that as the IV. The phrase “leniency design” or leniency instrument simply underscores that it’s the lenient vs. strict tendencies of the decision-maker that provide the exogenous variation.
A leniency IV design typically involves constructing an instrument like “the leave-out mean decision rate of the assigned examiner.” This could be, for instance, the fraction of previous similar cases that the examiner approved (excluding the current case). That number captures how lenient or strict they generally are. Because assignment is random, some individuals get a high-leniency examiner and others a low-leniency examiner, creating exogenous variation in treatment. By comparing outcomes across these, one can identify the causal effect of the treatment. The term “leniency” highlights that it’s the discretionary toughness of the examiner that we’re leveraging.
34.8.2.3 Examples in Economics
Many influential studies across economics and related fields have employed examiner or judge IV designs to answer causal questions. Below are several prominent examples illustrating the range of applications and findings:
Criminal Sentencing and Recidivism: In his seminal study, Kling (2006) examined the effect of incarceration length on ex-prisoners’ labor market outcomes. He used the random assignment of judges as an instrument, capitalizing on the fact that some judges are harsher (give longer sentences) and others more lenient. This judge IV strategy has since been used extensively to study how prison time impacts future criminal behavior and employment.
Pre-Trial Detention Decisions: The leniency design is also applied to bail and pre-trial release. Dobbie, Goldin, and Yang (2018) use the fact that arraignment judges vary in their tendency to set bail (versus release defendants) as an instrument to study the impact of pre-trial detention on defendants’ case outcomes and future behavior. Because defendants are quasi-randomly assigned to bail judges, this approach isolates how being jailed before trial causally affects outcomes like conviction or re-offense. These authors and others find, for example, that having a more lenient bail judge (who releases you pre-trial) leads to better long-run outcomes compared to a strict judge, indicating that pre-trial detention can have harmful causal effects.
Juvenile Incarceration and Life Outcomes: In a related vein, Aizer and Doyle Jr (2015) studied the effect of juvenile detention on high school completion and adult crime. They leveraged the random assignment of juvenile court judges, where some judges were more likely to incarcerate young offenders than others. This judge IV design revealed large negative causal impacts of juvenile incarceration on educational attainment and an increase in adult crime, evidence that sentencing leniency in youth can dramatically alter life trajectories (results consistent with the general pattern found in other judge IV studies of incarceration). This application illustrates how judicial decisions in youth have been treated as natural experiments.
Disability Insurance and Labor Supply: In the realm of social insurance, Maestas, Mullen, and Strand (2013) used an examiner design to determine whether receiving disability benefits discourages work. Each disability claim is assigned to a disability examiner, and some examiners approve benefits at higher rates than others. By using the quasi-random examiner assignment as an instrument, they found that for applicants on the margin of eligibility, receiving Disability Insurance caused a significant reduction in employment compared to if they had been denied. They report that about 23% of applicants are affected by which examiner they get, and those who were allowed benefits due to a lenient examiner would have had substantially higher employment rates had they instead been assigned a stricter examiner (and thus been denied). This study is a prime example of using medical or administrative examiner assignments to identify a policy’s effect.
Patent Grants and Innovation: Examiner designs are not limited to courts or social programs; they have been applied in innovation economics as well. Farre-Mensa, Hegde, and Ljungqvist (2020) analyze the value of obtaining a patent for startups by exploiting the U.S. Patent Office’s quasi-random assignment of applications to patent examiners. Some patent examiners are much more lenient (more likely to grant a patent) than others, effectively creating a “patent lottery”. The authors use examiner leniency as an instrument for whether a startup’s patent is approved. They find striking results: startups that “won” the lottery by drawing a lenient examiner had 55% higher employment growth and 80% higher sales five years later on average, compared to similar startups that ended up with a strict examiner and thus didn’t get the patent. This suggests that patent grants have a large causal impact on firm growth. This study showcases an examiner design in a regulatory/innovation setting – the term leniency IV in this case refers to the examiner’s propensity to allow patents.
Business Accelerators and Firm Growth: In an entrepreneurial finance context, González-Uribe and Reyes (2021) evaluate the impact of getting accepted into a business accelerator. Admission to the accelerator was determined by panels of judges scoring startup applicants, and the judges’ scoring leniency varied randomly across groups. The researchers exploit this by constructing an instrument based on the generosity of the judges’ scores for each applicant. They find that participating in the accelerator had a dramatic effect: startups that just made it in (thanks to generous-scoring judges) grew about 166% more in revenue than those that just missed the cutoff. This is an example of a “judge leniency” design outside of a courtroom – here the “judges” were competition evaluators, and their leniency in scoring provided the exogenous variation in program entry. It demonstrates that the examiner/judge IV approach can be applied to settings like business program evaluations or any scenario with selection committees.
These examples illustrate how examiner/judge (leniency) IV designs have been used in a wide array of empirical settings: from judicial decisions about bail, sentencing, and juvenile detention, to administrative adjudications on disability and bankruptcy, to regulatory approvals like patents, to evaluation panels in business or education contexts. In each case, the randomness of assignment and the differing “strictness” of the decision-makers create a natural experiment that researchers harness to estimate causal effects.
Why are these designs so valuable? They allow analysts to address the problem of unobserved heterogeneity or selection bias in observational data. Normally, people who receive a treatment (go to prison, get a benefit, win an award) may differ systematically from those who don’t, confounding simple comparisons. But if an outside examiner’s quasi-random decision determines who gets the treatment, we have a credible instrument to break that link. As one article notes, this approach has become quite popular as a reliable way to recover causal effects, even as many other attempted instruments face skepticism. The trade-off is that one must have a context where such random examiner assignment occurs and must carefully check the assumptions (e.g. truly random assignment, no direct effect of the examiner on outcomes aside from via treatment). When those conditions are met, examiner and judge IV designs provide compelling evidence on causal relationships that would be hard to identify otherwise.
34.8.2.4 Examples in Marketing
In marketing research, analogous setups can be constructed by identifying quasi-random sources of variation in decision-makers’ behaviors—such as sales representatives, regional managers, or customer service agents—who differ systematically in their tendency to approve discounts, upgrade customers, or resolve complaints favorably. These agents’ “leniency” can serve as an instrument for treatment assignment, enabling researchers to isolate causal effects in observational data where randomization is infeasible.
This analogical use of judge leniency introduces a powerful framework for addressing endogeneity in business contexts, allowing us to disentangle the effect of marketing actions (e.g., discounts, loyalty offers) from the confounding influence of customer selection or targeting bias.
| Judge Analog | Case Analog | Instrument / Causal Variation | Use Case / Research Question | Potential Outcomes |
|---|---|---|---|---|
| Ad reviewer | Submitted ad | Reviewer identity, shift rotation | Effect of ad rejection or delay on sales | CTR, sales, acquisition |
| Search ranker | Product view/visit | Random tie-breaking in rank | Impact of product ranking on behavior | Purchases, engagement |
| Sales rep | Customer inquiry | Agent assignment variation | Salesperson influence on conversion | Conversion, satisfaction |
| CSR rep | Complaint or service issue | Shift schedule, escalation rules | Does service response tone affect churn? | Retention, NPS |
| Matching algorithm | Influencer-brand pairing | Batch assignment randomness | Does match quality affect campaign ROI? | ROI, awareness |
| Moderator | User post / ad | Moderator stringency variation | Enforcement effect on trust and activity | Engagement, advertiser trust |
| Grant reviewer | Startup or proposal | Panel assignment, reviewer fixed effects | Causal effect of grant approval on growth | Marketing scaling, performance |
34.8.2.5 Formal Setup and Notation
We define the setup formally as follows:
- Let \(i = 1, \dots, n\) index individuals.
- Each individual has two outcomes of interest:
- \(D_i\): the treatment decision, made by the decision maker (e.g., bail granted or not).
- \(Y_i\): the final outcome, potentially affected by \(D_i\) (e.g., rearrest, discharge success).
- Each individual is randomly assigned to one of \(K\) decision makers: \(Q_i \in \{0, 1, \dots, K - 1\}\).
- We define potential treatment outcomes as:
- \(D_i(q)\): the treatment decision if individual \(i\) were assigned to decision maker \(q\).
- We observe only the realized \(D_i = D_i(Q_i)\).
Note: There is no meaningful ordering of \(Q_i\). The variation is purely categorical, not ordinal.
We also define potential final outcomes:
- \(Y_i(D_i(q), q)\): the final outcome if individual \(i\) is assigned to decision maker \(q\), receives treatment \(D_i(q)\).
When conducting IV, we focus on the reduced form and first-stage variation induced by \(Q_i\), and seek to shut down the direct effect of \(Q_i\) on \(Y_i\), conditioning only on \(D_i\).
We first consider the variation in \(D_i\) across \(Q_i\), potentially conditioning on observed covariates \(W_i\).
- Assume conditional ignorability: assignment to \(Q_i\) is as good as random given \(W_i\).
- In the simplest case, \(W_i\) contains only a constant (i.e., unadjusted analysis).
We can define:
\[ \tau_{q, q'} = \mathbb{E}[D_i \mid Q_i = q] - \mathbb{E}[D_i \mid Q_i = q'] \]
This is the relative effect of decision maker \(q\) vs. \(q'\) on treatment assignment.
Define:
\[ \mu_D(q) = \mathbb{E}[D_i \mid Q_i = q] \]
- This is judge \(q\)’s average leniency (i.e., how often they assign the treatment).
- Estimated via simple regression:
\[ D_i = Q_i \mu_D + u_i \]
Where \(Q_i\) is a vector of \(K\) dummies. Then \(\hat{\mu}_D(q)\) are the fitted means.
To isolate judge-level variation while adjusting for baseline differences (e.g., location), we control for \(W_i\):
\[ D_i = Q_i \mu_D + W_i \gamma + u_i \]
- Here, \(\mu_D(q)\) reflects conditional leniency, net of \(W_i\).
- Define the predicted value:
\[ Z_i = \hat{D}_i^\perp \]
This is the residualized leniency score, representing how lenient decision maker \(Q_i\) is, beyond what is expected from covariates \(W_i\).
Interpreting the Instrument \(Z_i\)
- \(Z_i\) reflects within-location variation in decision maker behavior.
- It isolates judge-specific variation that is not confounded by observable case-level or court-level factors.
- Mechanically, we define the residualized predicted treatment as:
\[ \hat{D}_i^\perp = \frac{1}{n} \left( \sum_i \underbrace{1(Q_i = q) D_i}_{\text{judge mean}} - \sum_i \underbrace{1(W_i = w) D_i}_{\text{location mean}} \right) \]
- The judge mean captures the average treatment assigned by judge \(q\).
- The location mean captures the average treatment assigned across individuals with the same observable characteristics \(W_i = w\) (e.g., court, time window).
- Subtracting the location mean residualizes the judge effect by removing location-specific variation.
The goal is to extract only the variation across judges that is orthogonal to systematic location-level treatment patterns.
Why Is This Re-centering Necessary?
The raw leniency score \(\mu_D(q) = \mathbb{E}[D_i \mid Q_i = q]\) may reflect:
- Actual judge discretion, but also
- Systematic differences in case mix, depending on location or time of day
This can bias the instrument if judges are not assigned uniformly across these contexts.
By centering judge-level means relative to the mean outcome in their location, we obtain a more meaningful instrument:
- It now reflects how lenient this judge is relative to their local peer group, controlling for observable confounding.
Once we apply this residualization:
- We obtain a “recentered” leniency measure, which reflects within-location differences in decision-maker behavior.
- This measure is commonly used in empirical IV applications (e.g., in criminal justice, bankruptcy courts, asylum decisions).
This aligns with real-world practice in empirical work, which often uses leave-one-out versions of \(\mu_D(Q_i)\) to avoid mechanical endogeneity.
Why use leave-one-out?
- Including the individual’s own outcome in the estimation of their instrument can induce endogeneity (mechanical correlation).
- The leave-one-out leniency score for judge \(q\) is:
\[ \tilde{\mu}_D^{(-i)}(q) = \frac{1}{n_q - 1} \sum_{j \ne i, Q_j = q} D_j \]
Where \(n_q\) is the number of individuals assigned to judge \(q\).
- This ensures that the instrument is uncorrelated with individual-level shocks, a key IV requirement.
We can compute residualized outcomes by subtracting out location-level variation, just like we did with leniency:
\[ \hat{Y}_i^\perp = \hat{Y}_i - \mathbb{E}[Y_i \mid W_i] \]
This helps us distinguish how much of the variation in outcomes is due to judge effects, rather than location-level factors.
- Even after controlling for \(W_i\), we often still observe meaningful variation in \(Y_i\) across judges.
- This implies that judge assignment induces variation in outcomes, even when holding location and case mix fixed.
34.8.2.6 Assumptions
-
Relevance:
- The instrument \(Z_i\) (e.g., judge leniency) must be strongly correlated with \(D_i\).
- That is, \(\mathbb{E}[D_i \mid Z_i]\) must vary meaningfully across values of \(Z_i\).
-
Exclusion:
- The instrument must affect the outcome only through \(D_i\).
- That is, \(Q_i\) should not have a direct effect on \(Y_i\) once we control for \(D_i\).
-
Monotonicity (G. W. Imbens and Angrist 1994):
- The effect of the instrument should not “flip signs” across units.
- If judge \(q\) is more lenient than \(q'\), then they are more lenient for everyone.
Note: The exclusion and monotonicity assumptions are not directly testable and can be controversial. We’ll return to this in more depth later.
34.8.2.7 One vs. Many Instruments
In many applied papers, researchers use the leniency score \(Z_i = \hat{D}_i^\perp\) rather than judge dummies directly.
Why?
-
Computational Simplicity:
- Using \(Z_i\) avoids estimating an over-identified system (i.e., one instrument per judge).
- This speeds up computation, especially in large datasets.
-
Ease of Visualization:
- Researchers often plot reduced-form and first-stage coefficients against leniency.
- This offers intuitive visual evidence of instrument strength and outcome response.
-
First Stage Power:
- In a just-identified model, checking the strength of the instrument (e.g., F-statistic) is straightforward.
- In contrast, many-instrument settings can obscure weak instrument issues.
Recall the 2SLS estimator in matrix form:
\[ \hat{\beta}_{2SLS} = \frac{D'Q(Q'Q)^{-1}Q'Y}{D'Q(Q'Q)^{-1}Q'D} = \frac{\hat{D}'Y}{\hat{D}'D} \]
This highlights a key point:
- Using many instruments (judge dummies) and projecting onto them,
- or using the predicted value \(\hat{D}_i\) as a single instrument,
are algebraically equivalent in the absence of controls.
- Adding controls just residualizes \(D_i\), \(Y_i\), and \(Z_i\) with respect to \(W_i\).
So which approach is better?
- The core identifying variation is still the random assignment to \(K\) judges.
- Collapsing that variation into a predicted value \(Z_i\) does not change the source of randomness.
- However, using the predicted value may obsure the experimental structure.
While point estimates may be equivalent, the inference can differ:
- If we use \(\hat{\mu}_D(q)\) as the first-stage effect, we ignore the sampling uncertainty in estimating these means.
- The variance of \(\hat{D}_i^\perp\) does not account for variability in the projection, leading to potentially understated standard errors.
This issue is closely related to the many instrument problem, and arises especially when \(K\) is large or judge assignment is sparse.
In many empirical cases:
- The just-identified leniency instrument and over-identified judge-dummy approach yield similar standard errors.
- This occurs when \(\hat{\mu}_D(q)\) is estimated with high precision (i.e., many observations per judge).
The most important advantage of leniency instruments is that they naturally handle the “own-observation” bias.
- In the naive case, \(\hat{\mu}_D(q)\) includes individual \(i\)’s own treatment \(D_i\):
- This introduces mechanical endogeneity, as the instrument is correlated with the error in \(Y_i\).
- The leave-one-out leniency score corrects this:
\[ \tilde{\mu}_D^{(-i)}(q) = \frac{1}{n_q - 1} \sum_{\substack{j \ne i \\ Q_j = q}} D_j \]
- Researchers construct \(Z_i\) using \(\tilde{\mu}_D^{(-i)}(Q_i)\), which excludes \(i\)’s data from their own instrument.
This is essentially a finite-sample approximation to jackknife IV (JIVE).
- The bias corrected by LOO is exactly the one that arises in many-instrument IV in small samples.
- The correction is especially important when the number of judges per location is moderate or small.
Given that the leniency approach can be understood as a form of JIVE (J. D. Angrist, Imbens, and Krueger 1999), why not go further ? U-JIVE (Unbiased JIVE) is a modern refinement developed to directly address these issues in finite samples (Kolesà et al. 2013).
- With many instruments or many fixed effects (e.g., location and time dummies), we can face the same inference problems.
- U-JIVE provides a consistent and unbiased estimator even in these challenging setups.
34.8.2.8 Testing the Exclusion Restriction
The exclusion restriction requires that judge assignment affects the outcome only through treatment—i.e., \(Q_i\) affects \(Y_i\) only through \(D_i\).
This is challenging to test directly, but we can probe its plausibility using tools familiar from RCTs and observational causal inference: covariate balance checks.
Step 1: Predict Propensity Scores
- Compute the first-stage predicted treatment: \(\hat{\mu}_D(Q_i)\)
- This is judge \(Q_i\)’s estimated leniency (possibly residualized)
- Use this as a “propensity score” for treatment \(D_i\)
Step 2: Test Covariate Balance Across Leniency
- Regress observable covariates \(X_i\) on \(\hat{\mu}_D(Q_i)\)
- If the assignment of judges is random (conditional on covariates), we should see no systematic relationship between covariates and predicted treatment
This is analogous to testing for pre-treatment balance in randomized experiments.
See Table 1 of Dobbie, Goldsmith-Pinkham, and Yang (2017), which displays descriptive statistics and tests for covariate balance across predicted leniency scores. This is now a standard empirical diagnostic in papers using judge IV designs.
If covariates vary significantly with \(\hat{\mu}_D(Q_i)\), the exclusion assumption is questionable—it may indicate that judge assignment is confounded with case characteristics.
34.8.2.9 Testing the Monotonicity Assumption
The monotonicity assumption requires that if one judge is more lenient than another, they are more lenient for everyone—i.e., no individual who is treated by a strict judge would have been untreated by a lenient one.
This is subtle and particularly hard to test in multi-judge (non-binary instrument) designs.
Monotonicity violations imply violations of the LATE interpretation—our IV may no longer estimate a meaningful average causal effect.
Recent work attempts to develop testable implications of monotonicity (Kitagawa 2015; Frandsen, Lefgren, and Leslie 2023).
Let:
\(D\) be a binary treatment
\(Z\) a binary instrument (e.g., judge assignment)
\(Y\) the outcome of interest
Define the joint distributions:
- \(P(y, d) = \mathbb{P}(Y = y, D = d \mid Z = 1)\)
- \(Q(y, d) = \mathbb{P}(Y = y, D = d \mid Z = 0)\)
Kitagawa (2015) shows that in the binary IV case if the IV is valid and monotonic, then:
\[ \begin{aligned} P(B, 1) - Q(B, 1) &\ge 0 \\ P(B, 0) - Q(B, 0) &\ge 0 \end{aligned} \]
Where \(B\) is any set of outcomes (e.g., \(Y \in \{1\}\)). These inequalities follow from the complier potential outcome structure under monotonicity.
These are testable implications. Violations suggest either invalid instruments or monotonicity failures.
In judge IV designs, the instrument is not binary. Frandsen, Lefgren, and Leslie (2023) extended Kitagawa (2015) idea to this case.
Key idea:
Map multiple judges to a scalar leniency index, \(Z_i = \hat{\mu}_D(Q_i)\)
Discretize \(Z_i\) if needed, then apply Kitagawa-style tests
Challenges:
The mapping introduces estimation error and noise
Tests rely on finite-sample approximations and may be underpowered
Still, these tests provide useful diagnostic tools to evaluate monotonicity plausibility.
A practical question: what can we do if the exclusion or monotonicity assumptions fail?
- Estimating bounds on the treatment effect under partial violations
- Exploring subgroup monotonicity (e.g., within strata where judges are plausibly rankable)
- Using alternative identification strategies (e.g., weaker forms of LATE)
In other words, all is not lost—but interpretation becomes more cautious and subtle.
Even when assumptions are reasonable, inference remains challenging in judge-IV setups.
- Many instruments \(\to\) weak instrument concerns
- Many controls (fixed effects) \(\to\) finite-sample bias and overfitting
- Heteroskedasticity \(\to\) robust inference is tricky
34.8.3 Proxy Variables
In applied business and economic analysis, we often confront a frustrating reality: the variables we truly care about—like brand loyalty, employee ability, or investor sentiment—are not directly observable. Instead, we rely on proxy variables, which are observable measures that stand in for these latent or omitted variables. Though useful, proxy variables must be used with care, as they introduce their own risks, most notably measurement error and incomplete control of endogeneity.
A proxy variable is an observed variable used in place of a variable that is either unobservable or omitted from a model. It is typically used under the assumption that it is correlated with the latent variable and explains some of its variation.
Let:
\(X^*\) be the latent (unobserved) variable,
\(X\) be the observed proxy,
\(Y\) be the outcome.
We may desire to estimate: \[ Y = \beta_0 + \beta_1 X^* + \varepsilon, \] but since \(X^*\) is unavailable, we instead estimate:
\[ Y = \beta_0 + \beta_1 X + u. \]
The effectiveness of this approach hinges on whether \(X\) can validly stand in for \(X^*\).
34.8.3.1 Proxy Use and Omitted Variable Bias
Proxy variables are sometimes used as substitutes for omitted variables that cause endogeneity. Including a proxy can reduce endogeneity, but it will not generally eliminate bias, unless strict conditions are met.
Key Insight: Including a proxy does not allow us to estimate the effect of the omitted variable; rather, it helps mitigate the bias introduced by its omission.
To be more precise, let’s consider a classic omitted variable setup:
Suppose the true model is: \[ Y = \beta_0 + \beta_1 X + \beta_2 Z + \varepsilon, \] but \(Z\) is omitted from the estimation. If \(Z\) is correlated with \(X\), the OLS estimate of \(\beta_1\) will be biased.
Now, suppose we have a proxy \(Z_p\) for \(Z\). Including \(Z_p\) in the regression: \[ Y = \beta_0 + \beta_1 X + \beta_2 Z_p + u \] can help reduce the bias if \(Z_p\) meets the following criteria.
Let \(Z\) be the unobserved variable and \(Z_p\) be the proxy. Then, \(Z_p\) is a valid proxy if:
- Correlation: \(Z_p\) is correlated with \(Z\) (i.e., \(\text{Cov}(Z_p, Z) \ne 0\)).
- Residual Independence: The residual variation in \(Z\) unexplained by \(Z_p\) is uncorrelated with all regressors (including \(Z_p\) and \(X\)): \[ Z = \gamma_0 + \gamma_1 Z_p + \nu, \quad \text{where } \text{Cov}(\nu, X) = \text{Cov}(\nu, Z_p) = 0. \]
- No direct effect: \(Z_p\) affects \(Y\) only through \(Z\) (or at least not directly).
Violation of these conditions can lead to biased or inconsistent estimates.
34.8.3.2 Example: IQ as a Proxy for Ability in Wage Regressions
In labor economics, researchers often study the effect of education on wages. But ability—an unobservable factor—also affects both education and wages, leading to omitted variable bias.
Let:
\(Y\) = wage,
\(X\) = education,
\(Z^*\) = ability (unobserved),
\(Z\) = IQ test score (proxy for ability).
Suppose the true model is: \[ \text{wage} = \beta_0 + \beta_1 \text{education} + \beta_2 \text{ability} + \varepsilon. \]
Since ability is unobserved, we estimate: \[ \text{wage} = \beta_0 + \beta_1 \text{education} + \beta_2 \text{IQ} + u, \] under the assumption: \[ \text{ability} = \gamma_0 + \gamma_1 \text{IQ} + \nu, \] with \(\text{Cov}(\nu, \text{education}) = \text{Cov}(\nu, \text{IQ}) = 0\).
This inclusion of IQ helps reduce endogeneity but does not identify the pure effect of ability unless all variation in ability is captured by IQ.
34.8.3.3 Pros and Cons of Proxy Variables
Advantages
- Make latent variables measurable: Allows analysis of constructs that cannot be directly observed.
- Practicality: Makes use of available data to address endogeneity.
- Improved specification: Can reduce omitted variable bias if proxies are well chosen.
Disadvantages
-
Measurement error: Proxies usually include noise, causing attenuation bias (i.e., coefficients biased toward zero).
If \(X = X^* + \nu\), with \(\nu\) classical measurement error (zero mean, uncorrelated with \(X^*\) and \(\varepsilon\)), then: \[ \text{plim}(\hat{\beta}_1) = \lambda \beta_1, \quad \text{where } \lambda = \frac{\sigma^2_{X^*}}{\sigma^2_{X^*} + \sigma^2_\nu} < 1. \]
Interpretation issues: Coefficients on proxies conflate the causal effect with proxy quality.
Insufficient control: Proxies only partially reduce omitted variable bias unless they meet strict independence conditions.
34.8.3.4 Empirical Illustration: Simulating Attenuation Bias
set.seed(2025)
n <- 1000
ability <- rnorm(n) # latent variable
IQ <- ability + rnorm(n, sd = 0.5) # proxy variable
education <- 12 + 0.5 * ability + rnorm(n) # correlated regressor
wage <- 20 + 1.5 * education + 2 * ability + rnorm(n) # true model
# Model using education only (omitted variable bias)
mod1 <- lm(wage ~ education)
# Model using education and proxy
mod2 <- lm(wage ~ education + IQ)
summary(mod1)
#>
#> Call:
#> lm(formula = wage ~ education)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -7.4949 -1.3590 -0.0082 1.3766 6.6601
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 10.51325 0.71353 14.73 <2e-16 ***
#> education 2.28903 0.05918 38.68 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 2.061 on 998 degrees of freedom
#> Multiple R-squared: 0.5999, Adjusted R-squared: 0.5995
#> F-statistic: 1496 on 1 and 998 DF, p-value: < 2.2e-16
summary(mod2)
#>
#> Call:
#> lm(formula = wage ~ education + IQ)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -5.3224 -0.9052 0.0523 0.9370 4.5822
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 17.96426 0.49599 36.22 <2e-16 ***
#> education 1.67098 0.04114 40.62 <2e-16 ***
#> IQ 1.55953 0.04096 38.07 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 1.317 on 997 degrees of freedom
#> Multiple R-squared: 0.8369, Adjusted R-squared: 0.8366
#> F-statistic: 2558 on 2 and 997 DF, p-value: < 2.2e-16Observe how including the proxy reduces the bias in the coefficient on education, even if it doesn’t eliminate it entirely.
34.8.3.5 Example: Marketing — Brand Loyalty
Suppose you’re modeling the effect of brand loyalty (\(X^*\)) on repeat purchase (\(Y\)). Since loyalty is latent, we might use:
- Number of prior purchases,
- Duration of current brand use,
- Membership in loyalty programs.
These proxies are likely to be correlated with true loyalty, but none is a perfect substitute.
# Simulating attenuation bias with a proxy
set.seed(42)
n <- 1000
X_star <- rnorm(n) # true unobserved brand loyalty
proxy <- X_star + rnorm(n, sd = 0.6) # proxy with measurement error
error <- rnorm(n)
Y <- 3 + 2 * X_star + error # true model
# Model using the proxy variable
model_proxy <- lm(Y ~ proxy)
summary(model_proxy)
#>
#> Call:
#> lm(formula = Y ~ proxy)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -4.3060 -1.0130 -0.0018 0.9131 4.5493
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 2.98737 0.04584 65.17 <2e-16 ***
#> proxy 1.45513 0.03921 37.11 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 1.449 on 998 degrees of freedom
#> Multiple R-squared: 0.5798, Adjusted R-squared: 0.5794
#> F-statistic: 1377 on 1 and 998 DF, p-value: < 2.2e-16Observe that the estimated coefficient on proxy is less than the true coefficient (2), due to measurement error.
34.8.3.6 Example: Finance — Investor Sentiment
Investor sentiment affects market movements but cannot be directly measured. Proxies include:
Put-call ratios
Bullish/bearish sentiment surveys,
Volume of IPO activity,
Retail investor trading flows.
These capture different dimensions of sentiment, and their effectiveness varies by context.
34.8.3.7 Strategies to Improve Proxy Use
Multiple proxies: Use several proxies and combine them via factor analysis or PCA
Instrumental variables: If a valid instrument exists for the proxy, use two-stage least squares to correct for measurement error.
Latent variable models: Structural Equation Modeling (SEM) allows estimation of models with latent variables explicitly.
Proxy variables are valuable tools in empirical research when used with caution. They offer a bridge between theory and data when important variables are unobservable. However, this bridge is built on assumptions—especially regarding correlation, measurement error, and residual independence—that must be carefully justified.
Key Takeaway: A proxy can reduce bias from omitted variables but introduces its own risks—especially measurement error and interpretive ambiguity. The best practice is to use proxies transparently, test assumptions when possible, and consider alternative solutions such as instruments or structural models.