Data can be defined broadly as any set of values, facts, or statistics that can be used for reference, analysis, and drawing inferences. In research, data drives the process of understanding phenomena, testing hypotheses, and formulating evidence-based conclusions. Choosing the right type of data (and understanding its strengths and limitations) is critical for the validity and reliability of findings.
A foundational way to categorize data is by whether it is qualitative (non-numerical) or quantitative (numerical). These distinctions often guide research designs, data collection methods, and analytical techniques.
| Qualitative | Quantitative |
|---|---|
| Examples: In-depth interviews, focus groups, case studies, ethnographies, open-ended questions, field notes | Examples: Surveys with closed-ended questions, experiments, numerical observations, structured interviews |
| Nature: Text-based, often descriptive, subjective interpretations | Nature: Numeric, more standardized, objective measures |
| Analysis: Thematic coding, content analysis, discourse analysis | Analysis: Statistical tests, regression, hypothesis testing, descriptive statistics |
| Outcome: Rich context, detailed understanding of phenomena | Outcome: Measurable facts, generalizable findings (with appropriate sampling and design) |
Deep Understanding: Captures context, motivations, and perceptions in depth.
Flexibility: Elicits new insights through open-ended inquiry.
Inductive Approaches: Often used to build new theories or conceptual frameworks.
Measurement and Comparison: Facilitates measuring variables and comparing across groups or over time.
Generalizability: With proper sampling, findings can often be generalized to broader populations.
Hypothesis Testing: Permits the use of statistical methods to test specific predictions or relationships.
Qualitative:
Findings may be difficult to generalize if samples are small or non-representative.
Analysis can be time-consuming due to coding and interpreting text.
Potential for researcher bias in interpretation.
Quantitative:
May oversimplify complex human behaviors or contextual factors by reducing them to numbers.
Validity depends heavily on how well constructs are operationalized.
Can miss underlying meanings or nuances not captured in numeric measures.
Even within quantitative data, there are further distinctions based on the level of measurement. This classification is crucial for determining which statistical techniques are appropriate:
Nominal: Categorical data with no inherent order (e.g., gender, blood type, eye color).
Ordinal: Categorical data with a specific order or ranking but without consistent intervals between ranks (e.g., Likert scale responses: “strongly disagree,” “disagree,” “neutral,” “agree,” “strongly agree”).
Interval: Numeric data with equal intervals but no true zero (e.g., temperature in Celsius or Fahrenheit).
Ratio: Numeric data with equal intervals and a meaningful zero (e.g., height, weight, income).
The level of measurement affects which statistical tests (like t-tests, ANOVA, correlations, regressions) are valid and how you can interpret differences or ratios in the data.
Beyond observational structure, there are multiple other dimensions used to classify data:
Primary Data: Collected directly by the researcher for a specific purpose (e.g., firsthand surveys, experiments, direct measurements).
Secondary Data: Originally gathered by someone else for a different purpose (e.g., government census data, administrative records, previously published datasets).
Structured Data: Organized in a predefined manner, typically in rows and columns (e.g., spreadsheets, relational databases).
Semi-Structured Data: Contains organizational markers but not strictly tabular (e.g., JSON, XML logs, HTML).
Unstructured Data: Lacks a clear, consistent format (e.g., raw text, images, videos, audio files).
Characterized by the “3 Vs”: Volume (large amounts), Variety (diverse forms), and Velocity (high-speed generation).
Requires specialized computational tools (e.g., Hadoop, Spark) and often cloud-based infrastructure for storage and processing.
Can be structured or unstructured (e.g., social media feeds, sensor data, clickstream data).
Another primary way to categorize data is by how observations are collected over time. This classification shapes research design, analytic methods, and the types of inferences we can make. Four major types here are:
| Type | Advantages | Limitations |
|---|---|---|
| Cross-Sectional Data | Simple, cost-effective, good for studying distributions or correlations at a single time point. | Lacks temporal information, can only infer associations, not causal links. |
| Time Series Data | Enables trend analysis, seasonality detection, and forecasting. | Requires handling autocorrelation, stationarity issues, and structural breaks. |
| Repeated Cross-Sectional Data | Tracks shifts in population-level parameters over time; simpler than panel data. | Cannot track individual changes; comparability depends on consistent methodology. |
| Panel (Longitudinal) Data | Allows causal inference, controls for unobserved heterogeneity, tracks individual trajectories. | Expensive, prone to attrition, requires complex statistical methods. |
Cross-sectional data consists of observations on multiple entities (e.g., individuals, firms, regions, or countries) at a single point in time or over a very short period, where time is not a primary dimension of variation.
Examples
Key Characteristics
Advantages
Challenges
A typical cross-sectional regression model:
yi=β0+xi1β1+xi2β2+⋯+xi(k−1)βk−1+ϵi
where:
Time series data consists of observations on the same variable(s) recorded over multiple time periods for a single entity (or aggregated entity). These data points are typically collected at consistent intervals—hourly, daily, monthly, quarterly, or annually—allowing for the analysis of trends, patterns, and forecasting.
Examples
Key Characteristics
Advantages
Challenges
A time series typically consists of four key components:
A general linear time series model can be expressed as:
yt=β0+xt1β1+xt2β2+⋯+xt(k−1)βk−1+ϵt
Some Common Model Types
A simple time series regression:
yt=β0+x1β1+x2β2+x3β3+ϵt
Captures the effect of past values of an explanatory variable:
yt=β0+petδ0+pet−1δ1+pet−2δ2+ϵt
Long-Run Propensity: Measures the cumulative effect of explanatory variables over time:
LRP=δ0+δ1+δ2
A model incorporating lagged dependent variables:
GDPt=β0+β1GDPt−1+ϵt
For time series regression, standard OLS assumptions must be carefully examined. The following conditions affect estimation:
Finite Sample Properties
However, in time series settings, A3 often fails due to:
Several key models describe different time series behaviors:
Autoregressive Model (AR(p)): A process where current values depend on past values.
Moving Average Model (MA(q)): A process where past error terms influence current values.
Autoregressive Moving Average (ARMA(p, q)): A combination of AR and MA processes.
Autoregressive Conditional Heteroskedasticity (ARCH(p)): Models time-varying volatility.
Generalized ARCH (GARCH(p, q)): Extends ARCH by including past conditional variances.
When both the dependent and independent variables exhibit trending behavior, a regression may produce spurious results.
Spurious Regression Example
A simple regression with trending variables:
yt=α0+tα1+vt
xt=λ0+tλ1+ut
where
α1≠0 and λ1≠1
vt and ut are independent.
Despite no true relationship between xt and yt, estimating:
yt=β0+xtβ1+ϵt
results in:
We can also rewrite the equation as:
yt=β0+β1xt+ϵtϵt=α1t+vt
where β0=α0 and β1=0. Since xt is a deterministic function of time, ϵt is correlated with xt, leading to the usual omitted variable bias.
Solutions to Spurious Trends
The exogeneity assumption (A3) plays a crucial role in ensuring unbiased and consistent estimation in time series models. However, in many cases, the assumption is violated due to the inherent nature of time-dependent processes.
In a standard regression framework, we assume:
E(ϵt|x1,x2,...,xT)=0
which requires that the error term is uncorrelated with all past, present, and future values of the independent variables.
Common Violations of Exogeneity
In a simple regression model:
yt=β0+xtβ1+ϵt
the standard exogeneity assumption (A3) requires:
E(ϵt|x1,x2,...,xt,xt+1,...,xT)=0
However, in the presence of feedback, past errors affect future values of xt, leading to:
E(ϵt|xt+1,...,xT)≠0
Implication:
A dynamically specified model includes lagged dependent variables:
yt=β0+yt−1β1+ϵt
Exogeneity (A3) would require:
E(ϵt|y1,y2,...,yt,yt+1,...,yT)=0
However, since yt−1 depends on ϵt−1 from the previous period, we obtain:
Cov(yt−1,ϵt)≠0
Implication:
A finite distributed lag (FDL) model:
yt=β0+xtδ0+xt−1δ1+ϵt
assumes that the included lags fully capture the relationship between yt and past values of xt. However, if we omit relevant lags, the exogeneity assumption (A3):
E(ϵt|x1,x2,...,xt,xt+1,...,xT)=0
fails, as unmodeled lag effects create correlation between xt−2 and ϵt.
Implication:
If strict exogeneity (A3) fails, standard OLS assumptions no longer hold:
To address these issues, we can:
If strict exogeneity does not hold, we can instead assume A3a (Contemporaneous Exogeneity):
E(x′tϵt)=0
This weaker assumption only requires that xt is uncorrelated with the error in the same time period.
Key Differences from Strict Exogeneity
| Exogeneity Type | Requirement | Allows Dynamic Models? |
|---|---|---|
| Strict Exogeneity | E(ϵt|x1,x2,...,xT)=0 | No |
| Contemporaneous Exogeneity | E(x′tϵt)=0 | Yes |
With contemporaneous exogeneity, ϵt can be correlated with past and future values of xt.
This allows for dynamic specifications such as:
yt=β0+yt−1β1+ϵt
while still maintaining consistency under certain assumptions.
Deriving Large Sample Properties for Time Series
To establish consistency and asymptotic normality, we rely on the following assumptions:
However, the standard Weak Law of Large Numbers and Central Limit Theorem in OLS depend on A5 (Random Sampling), which does not hold in time series settings.
Since time series data exhibits dependence over time, we replace A5 (Random Sampling) with a weaker assumption:
Asymptotic Variance and Serial Correlation
The derivation of asymptotic variance depends on A4 (Homoskedasticity).
However, in time series settings, we often encounter serial correlation:
Cov(ϵt,ϵs)≠0for|t−s|>0
To ensure valid inference, standard errors must be corrected using methods such as Newey-West HAC estimators.
In time series analysis, a key assumption for OLS consistency is that the data-generating process exhibits A5a weak dependence (i.e., observations are not too strongly correlated over time). However, when yt and xt are highly persistent, standard OLS assumptions break down.
If a time series is not weakly dependent, it means:
Example: A classic example of a highly persistent process is a random walk:
yt=yt−1+ut
or with drift:
yt=α+yt−1+ut
where ut is a white noise error term.
A common way to transform non-stationary series into stationary ones is through first differencing:
Δyt=yt−yt−1=ut
Δyt=(Δxtβ)+(ϵt−ϵt−1)Δyt=Δxtβ+Δut
This ensures OLS estimation remains valid.
To formally determine whether a time series contains a unit root (i.e., is non-stationary), we test:
yt=α+ρyt−1+ut
Hypothesis Testing
Key Issues
The Dickey-Fuller test transforms the original equation by subtracting yt−1 from both sides:
Δyt=α+θyt−1+vt
where:
θ=ρ−1
Since yt follows a non-standard asymptotic distribution under H0, Dickey and Fuller derived specialized critical values.
Decision Rule
The standard DF test may fail due to two key limitations:
Solution:
Use the Augmented Dickey-Fuller test, which includes extra lags:
Δyt=α+θyt−1+γ1Δyt−1+⋯+γpΔyt−p+vt
Including lags of Δyt ensures a better-specified model.
If a series exhibits a deterministic trend, failing to include it biases the unit root test.
Example: If yt grows over time, a test without a trend component will falsely detect a unit root.
Solution: Include a deterministic time trend (t) in the regression:
Δyt=α+θyt−1+δt+vt
The ADF test generalizes the DF test by allowing for:
Regression Equation
Δyt=α+θyt−1+δt+γ1Δyt−1+⋯+γpΔyt−p+vt
where θ=1−ρ.
Hypotheses
Newey-West standard errors, also known as Heteroskedasticity and Autocorrelation Consistent (HAC) estimators, provide valid inference when errors exhibit both heteroskedasticity (i.e., A4 Homoskedasticity assumption is violated) and serial correlation. These standard errors adjust for dependence in the error structure, ensuring that hypothesis tests remain valid.
Key Features
The estimator is computed as:
ˆB=T−1T∑t=1e2tx′txt+g∑h=1(1−hg+1)T−1T∑t=h+1etet−h(x′txt−h+x′t−hxt)
where:
Choosing the Lag Length (g)
Selecting an appropriate lag truncation parameter (g) is crucial for balancing efficiency and bias. Common guidelines include:
Alternatively, data-driven methods can be used:
Newey-West Rule: g=⌊4(T/100)2/9⌋
Alternative Heuristic: g=⌊T1/4⌋
# Load necessary libraries
library(sandwich)
library(lmtest)
# Simulate data
set.seed(42)
T <- 100 # Sample size
time <- 1:T
x <- rnorm(T)
epsilon <- arima.sim(n = T, list(ar = 0.5)) # Autocorrelated errors
y <- 2 + 3 * x + epsilon # True model
# Estimate OLS model
model <- lm(y ~ x)
# Compute Newey-West standard errors
lag_length <- floor(4 * (T / 100) ^ (2 / 9)) # Newey-West rule
nw_se <- NeweyWest(model, lag = lag_length, prewhite = FALSE)
# Display robust standard errors
coeftest(model, vcov = nw_se)
#>
#> t test of coefficients:
#>
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 1.71372 0.13189 12.993 < 2.2e-16 ***
#> x 3.15831 0.13402 23.567 < 2.2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Serial correlation (also known as autocorrelation) occurs when error terms are correlated across time:
E(ϵtϵt−h)≠0for some h≠0
Steps for Detecting Serial Correlation
Regress et on xt and its lagged residual et−1:
et=γ0+x′tγ+ρet−1+vt
Test whether ρ is significantly different from zero.
Higher-Order Serial Correlation
To test for higher-order autocorrelation, extend the previous regression:
et=γ0+x′tγ+ρ1et−1+ρ2et−2+⋯+ρpet−p+vt
Step 1: Estimate an OLS Regression and Obtain Residuals
# Load necessary libraries
library(lmtest)
library(sandwich)
# Generate some example data
set.seed(123)
n <- 100
x <- rnorm(n)
y <- 1 + 0.5 * x + rnorm(n) # True model: y = 1 + 0.5*x + e
# Estimate the OLS regression
model <- lm(y ~ x)
# Obtain residuals
residuals <- resid(model)Step 2: Test for Autocorrelation in Residuals
# Create lagged residuals
lagged_residuals <- c(NA, residuals[-length(residuals)])
# Regress residuals on x and lagged residuals
autocorr_test_model <- lm(residuals ~ x + lagged_residuals)
# Summary of the regression
summary(autocorr_test_model)
#>
#> Call:
#> lm(formula = residuals ~ x + lagged_residuals)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -1.94809 -0.72539 -0.08105 0.58503 3.12941
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.008175 0.098112 0.083 0.934
#> x -0.002841 0.107167 -0.027 0.979
#> lagged_residuals -0.127605 0.101746 -1.254 0.213
#>
#> Residual standard error: 0.9707 on 96 degrees of freedom
#> (1 observation deleted due to missingness)
#> Multiple R-squared: 0.01614, Adjusted R-squared: -0.004354
#> F-statistic: 0.7876 on 2 and 96 DF, p-value: 0.4579
# Test if the coefficient of lagged_residuals is significant
rho <- coef(autocorr_test_model)["lagged_residuals"]
rho_p_value <-
summary(autocorr_test_model)$coefficients["lagged_residuals", "Pr(>|t|)"]
# Decision Rule
if (rho_p_value < 0.05) {
cat("Reject the null hypothesis: There is evidence of serial correlation.\n")
} else {
cat("Fail to reject the null hypothesis: No evidence of serial correlation.\n")
}
#> Fail to reject the null hypothesis: No evidence of serial correlation.Step 3: Testing for Higher-Order Serial Correlation
# Number of lags to test
p <- 2 # Example: testing for 2nd order autocorrelation
# Create a matrix of lagged residuals
lagged_residuals_matrix <- sapply(1:p, function(i) c(rep(NA, i), residuals[1:(n - i)]))
# Regress residuals on x and lagged residuals
higher_order_autocorr_test_model <- lm(residuals ~ x + lagged_residuals_matrix)
# Summary of the regression
summary(higher_order_autocorr_test_model)
#>
#> Call:
#> lm(formula = residuals ~ x + lagged_residuals_matrix)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -1.9401 -0.7290 -0.1036 0.6359 3.0253
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 0.006263 0.099104 0.063 0.950
#> x 0.010442 0.108370 0.096 0.923
#> lagged_residuals_matrix1 -0.140426 0.103419 -1.358 0.178
#> lagged_residuals_matrix2 -0.107385 0.103922 -1.033 0.304
#>
#> Residual standard error: 0.975 on 94 degrees of freedom
#> (2 observations deleted due to missingness)
#> Multiple R-squared: 0.02667, Adjusted R-squared: -0.004391
#> F-statistic: 0.8587 on 3 and 94 DF, p-value: 0.4655
# Joint F-test for the significance of lagged residuals
f_test <- car::linearHypothesis(higher_order_autocorr_test_model,
paste0("lagged_residuals_matrix", 1:p, " = 0"))
# Print the F-test results
print(f_test)
#>
#> Linear hypothesis test:
#> lagged_residuals_matrix1 = 0
#> lagged_residuals_matrix2 = 0
#>
#> Model 1: restricted model
#> Model 2: residuals ~ x + lagged_residuals_matrix
#>
#> Res.Df RSS Df Sum of Sq F Pr(>F)
#> 1 96 91.816
#> 2 94 89.368 2 2.4479 1.2874 0.2808
# Decision Rule
if (f_test$`Pr(>F)`[2] < 0.05) {
cat("Reject the null hypothesis: There is evidence of higher-order serial correlation.\n")
} else {
cat("Fail to reject the null hypothesis: No evidence of higher-order serial correlation.\n")
}
#> Fail to reject the null hypothesis: No evidence of higher-order serial correlation.Corrections for Serial Correlation
If serial correlation is detected, the following adjustments should be made:
| Problem | Solution |
|---|---|
| Mild serial correlation | Use Newey-West standard errors |
| Severe serial correlation | Use Generalized Least Squares or Prais-Winsten transformation |
| Autoregressive structure in errors | Model as an ARMA process |
| Higher-order serial correlation | Include lags of dependent variable or use HAC estimators with higher lag orders |
Repeated cross-sectional data consists of multiple independent cross-sections collected at different points in time. Unlike panel data, where the same individuals are tracked over time, repeated cross-sections draw a fresh sample in each wave.
This approach allows researchers to analyze aggregate trends over time, but it does not track individual-level changes.
Examples
Since repeated cross-sections do not track the same individuals, specific regression methods are used to analyze changes over time.
Combines multiple survey waves into a single dataset while controlling for time effects:
yi=xiβ+δ1y1+...+δTyT+ϵi
where:
yi is the outcome for individual i,
xi are explanatory variables,
yt are time period dummies,
δt captures the average change in outcomes across time periods.
Key Features:
Allows for different intercepts across time periods, capturing shifts in baseline outcomes.
Tracks overall population trends without assuming a constant effect of xi over time.
To test whether relationships between variables change over time (structural breaks), interactions between time dummies and explanatory variables can be introduced:
yi=xiβ+xiy1γ1+...+xiyTγT+δ1y1+...+δTyT+ϵi
Practical Application:
If xi represents education level and yt represents survey year, an interaction term can test whether the effect of education on income has changed over time.
Structural break tests help determine whether such time-varying effects are statistically significant.
Useful for policy analysis, where a policy might impact certain subgroups differently across time.
A simple approach to comparing aggregate trends:
ˉyt−ˉyt−1
Since repeated cross-sections do not track individuals, a synthetic cohort can be created by grouping observations based on shared characteristics:
| Advantage | Explanation |
|---|---|
| Tracks population trends | Useful for studying shifts in demographics, attitudes, and economic conditions over time. |
| Lower cost than panel data | Tracking individuals across multiple waves (as in panel studies) is expensive and prone to attrition. |
| No attrition bias | Unlike panel surveys, where respondents drop out over time, each wave draws a new representative sample. |
| Easier implementation | Organizations can design a single survey protocol and repeat it at set intervals without managing panel retention. |
| Disadvantage | Explanation |
|---|---|
| No individual-level transitions | Cannot track how specific individuals change over time (e.g., income mobility, changes in attitudes). |
| Limited causal inference | Since we observe different people in each wave, we cannot directly infer individual cause-and-effect relationships. |
| Comparability issues | Small differences in survey design (e.g., question wording or sampling frame) can make it difficult to compare across waves. |
To ensure valid comparisons across time:
Panel data (also called longitudinal data) consists of observations of the same entities over multiple time periods. Unlike repeated cross-sections, where new samples are drawn in each wave, panel data tracks the same individuals, households, firms, or regions over time, enabling richer statistical analysis.
Panel data combines cross-sectional variation (differences across entities) and time-series variation (changes within entities over time).
Examples
Structure
Types of Panels
| Advantage | Explanation |
|---|---|
| Captures individual trajectories | Allows for studying how individuals or firms evolve over time. |
| Controls for unobserved heterogeneity | Fixed effects models remove time-invariant individual characteristics. |
| Stronger causal inference | Difference-in-differences and FE models improve causal interpretation. |
| More efficient estimates | Exploits both cross-sectional and time-series variation. |
| Disadvantage | Explanation |
|---|---|
| Higher cost and complexity | Tracking individuals over time is resource-intensive. |
| Attrition bias | If certain individuals drop out systematically, results may be biased. |
| Measurement errors | Errors accumulate over time, leading to potential biases. |
Since we observe both individuals and time periods, we distinguish three types of variation:
| Estimate | Formula |
|---|---|
| Individual mean | ˉxi=1T∑txit |
| Overall mean | ˉx=1NT∑i∑txit |
| Overall variance | s2O=1NT−1∑i∑t(xit−ˉx)2 |
| Between variance | s2B=1N−1∑i(ˉxi−ˉx)2 |
| Within variance | s2W=1NT−1∑i∑t(xit−ˉxi)2 |
Note: s2O≈s2B+s2W
The Pooled Ordinary Least Squares estimator is the simplest way to estimate relationships in panel data. It treats panel data as a large cross-sectional dataset, ignoring individual-specific effects and time dependence.
The pooled OLS model is specified as:
yit=xitβ+ϵit
where:
yit is the dependent variable for individual i at time t,
xit is a vector of explanatory variables,
β is the vector of coefficients to be estimated,
ϵit=ci+uit is the composite error term.
ci is the unobserved individual heterogeneity.
uit is the idiosyncratic shock.
By treating all observations as independent, pooled OLS assumes no systematic differences across individuals beyond what is captured by xit.
For pooled OLS to be consistent and unbiased, the following conditions must hold:
For pooled OLS to be consistent, we require A3a:
E(x′it(ci+uit))=0
which holds if and only if:
Implication:
If ci is correlated with xit, pooled OLS is biased and inconsistent.
If ci is uncorrelated with xit, pooled OLS is consistent but inefficient.
Variance Decomposition in Panel Data
Since panel data contains both between-entity and within-entity variation, the total variance can be decomposed into:
s2O=s2B+s2W
where:
s2O = Overall variance (variation over time and across individuals),
s2B = Between variance (variation between individuals),
s2W = Within variance (variation within individuals over time).
Key Insight:
Pooled OLS does not separate within-individual and between-individual variation.
Fixed Effects models eliminate ci and use only within-individual variation.
Random Effects models use both within and between variation.
Robust Inference in Pooled OLS
If the standard assumptions fail, adjustments are necessary:
Comparing Pooled OLS with Alternative Panel Models
| Model | Assumption about ci | Uses Within Variation? | Uses Between Variation? | Best When |
|---|---|---|---|---|
| Pooled OLS | Assumes ci is uncorrelated with xit | ✅ Yes | ✅ Yes | No individual heterogeneity |
| Fixed Effects | Removes ci via demeaning | ✅ Yes | ❌ No | ci is correlated with xit |
| Random Effects | Assumes ci is uncorrelated with xit | ✅ Yes | ✅ Yes | ci is uncorrelated with xit |
When to Use Pooled OLS?
If individual heterogeneity is negligible
If panel is short (T is small) and cross-section is large (N is big)
If random effects assumption holds (E(x′itci)=0)
If these conditions fail, Fixed Effects or Random Effects models should be used instead.
In panel data, unobserved heterogeneity can arise when individual-specific factors (ci) influence the dependent variable. These effects can be:
The general model is:
yit=xitβ+ci+uit
where:
ci is the individual-specific effect (time-invariant),
uit is the idiosyncratic error (time-variant).
Comparing Fixed Effects and Random Effects
| Model | Assumption on ci | Uses Within Variation? | Uses Between Variation? | Best When |
|---|---|---|---|---|
| Fixed Effects | ci is correlated with xit | ✅ Yes | ❌ No | Unobserved heterogeneity bias present |
| Random Effects | ci is uncorrelated with xit | ✅ Yes | ✅ Yes | No correlation with regressors |
The Random Effects (RE) estimator is a Feasible Generalized Least Squares method used in panel data analysis. It assumes that individual-specific effects (ci) are uncorrelated with the explanatory variables (xit), allowing for estimation using both within-group (time variation) and between-group (cross-sectional variation).
The standard Random Effects model is:
yit=xitβ+ci+uit
where:
yit is the dependent variable for entity i at time t,
xit is a vector of explanatory variables,
β represents the coefficients of interest,
ci is the unobserved individual-specific effect (time-invariant),
uit is the idiosyncratic error (time-varying).
In contrast to the Fixed Effects model, which eliminates ci by demeaning the data, the Random Effects model treats ci as a random variable and incorporates it into the error structure.
For the Random Effects estimator to be consistent, the following assumptions must hold:
The idiosyncratic error term (uit) must be uncorrelated with regressors:
E(x′ituit)=0
This assumption ensures that within-period variation in the regressors does not systematically affect the error term.
A crucial assumption of the RE model is that the individual effect (ci) is uncorrelated with the explanatory variables:
E(x′itci)=0
This means that the individual-specific unobserved characteristics do not systematically affect the choice of explanatory variables.
The error term (uit) must be uncorrelated across time:
E(uituis)=0,∀t≠s
If this assumption fails:
Standard errors will be incorrect.
Generalized Least Squares adjustments or cluster-robust standard errors are required.
The RE estimator is a GLS estimator, meaning it is BLUE (Best Linear Unbiased Estimator) under homoskedasticity.
| Scenario | Efficiency of RE |
|---|---|
| A4 (Homoskedasticity) holds | RE is the most efficient estimator. |
| A4 fails (Heteroskedasticity or Serial Correlation) | RE remains more efficient than Pooled OLS but is no longer optimal. |
To efficiently estimate β, we transform the RE model using Generalized Least Squares.
Define the quasi-demeaned transformation:
˜yit=yit−θˉyi
˜xit=xit−θˉxi
where:
θ=1−√σ2uTσ2c+σ2u
The final RE regression equation is:
˜yit=˜xitβ+˜uit
which is estimated using GLS.
Also known as the Within Estimator, the FE model controls for individual-specific effects by removing them through transformation.
Key Assumption
If the RE assumption fails (E(x′itci)≠0), then:
However, FE only corrects bias from time-invariant factors and does not handle time-variant omitted variables.
Challenges with FE
To remove ci, we take the individual mean of the regression equation:
yit=xitβ+ci+uit
Averaging over time (T):
ˉyi=ˉxiβ+ci+ˉui
Subtracting the second equation from the first (i.e., within transformation):
(yit−ˉyi)=(xit−ˉxi)β+(uit−ˉui)
This transformation:
Eliminates ci, solving omitted variable bias.
Only uses within-individual variation.
The transformed regression is estimated via OLS:
yit−ˉyi=(xit−ˉxi)β+d1δ1+⋯+dT−2δT−2+(uit−ˉui)
where
dt is a time dummy variable, which equals 1 if the observation in the time periods t, and 0 otherwise. This variable is for period t=1,…,T−1 (one period omitted to avoid perfect multicollinearity).
δt is the coefficient on the time dummy, capturing aggregate shocks that affect all individual in period t.
Key Conditions for Consistency:
Strict Exogeneity (A3):
E[(xit−ˉxi)′(uit−ˉui)]=0
Time-invariant variables are dropped (e.g., gender, ethnicity). If you’re interested in the effect of these time-invariant variables, consider using either OLS or the between estimator.
Cluster-Robust Standard Errors should be used.
The Dummy Variable Approach is an alternative way to estimate Fixed Effects in panel data. Instead of transforming the data by demeaning (Within Transformation), this method explicitly includes individual dummy variables to control for entity-specific heterogeneity.
The general FE model is:
yit=xitβ+ci+uit
where:
ci is the unobserved, time-invariant individual effect (e.g., ability, cultural preferences, managerial style).
uit is the idiosyncratic error term (fluctuates over time and across individuals).
To estimate this model using the Dummy Variable Approach, we include a separate dummy variable for each individual:
yit=xitβ+d1δ1+...+dT−2δT−2+c1γ1+...+cn−1γn−1+uit
where:
ci is now modeled explicitly as a dummy variable (ciγi) for each individual.
dt are time dummies, capturing time-specific shocks.
δt are coefficients on time dummies, controlling for common time effects.
Interpretation of the Dummy Variables
The dummy variable ci takes a value of 1 for individual i and 0 otherwise:
ci={1if observation is for individual i0otherwise
These N dummy variables absorb all individual-specific variation, ensuring that only within-individual (over-time) variation remains.
Advantages of the Dummy Variable Approach
Limitations of the Dummy Variable Approach
An alternative way to eliminate individual-specific effects (ci) is to take first differences across time, rather than subtracting the individual mean.
The FE model:
yit=xitβ+ci+uit
Since ci is constant over time, taking the first difference:
yit−yi(t−1)=(xit−xi(t−1))β+(uit−ui(t−1))
This transformation removes ci completely, leaving a model that can be estimated using Pooled OLS.
Advantages of the First-Difference Approach
Limitations of the First-Difference Approach
| Approach | How it Works | Pros | Cons |
|---|---|---|---|
| Dummy Variable | Includes individual dummies (ci) in regression | Intuitive, easy to interpret | Computationally expensive for large N, standard errors may be incorrect |
| Within Transformation (Demeaning) | Subtracts individual mean from each variable | Computationally efficient, correct standard errors | Cannot estimate time-invariant variables |
| First-Difference Approach | Takes time differences to remove ci | Simple, works well for small T | Reduces sample size, introduces autocorrelation |
Key Insights
FE reduces variation by removing ci, which affects error variance:
ˆσ2ϵ=SSROLSNT−K
ˆσ2u=SSRFENT−(N+K)=SSRFEN(T−1)−K
Implication:
The variance of the error may increase or decrease because:
SSR can increase (since FE eliminates between variation).
Degrees of freedom decrease (as more parameters are estimated).
Research Questions
Mechanisms for Intergenerational Mobility
There are multiple pathways through which parental income influences child outcomes:
One way to measure the impact of income on human capital accumulation is:
%ΔHuman Capital%ΔParental Income
where human capital includes education, skills, and job market outcomes.
Income is measured in different ways to capture its long-term effects:
Key control variables must be exogenous to avoid bias. Bad Controls are those that are jointly determined with the dependent variable (e.g., mother’s labor force participation).
Exogenous controls:
Mother’s race
Birth location
Parental education
Household structure at age 14
The estimated model is:
Yijt=Xjtβi+Ijtαi+ϵijt
where:
i = test (e.g., academic test score).
j = individual (child).
t = time.
Xjt = observable child characteristics.
Ijt = parental income.
ϵijt = error term.
Grandmother’s Fixed-Effects Model
Since a child (j) is nested within a mother (m), and a mother is nested within a grandmother (g), we estimate:
Yijgmt=Xitβi+Ijtαi+γg+uijgmt
where:
g = Grandmother, m = Mother, j = Child, t = Time.
γg captures both grandmother and mother fixed effects.
The nested structure controls for genetic and fixed family environment effects.
Cluster standard errors at the family level to account for correlation in errors across generations.
Pros of Grandmother FE Model
Controls for genetics + fixed family background
Allows estimation of income effects independent of family background
Cons
Might not fully control for unobserved heterogeneity
Measurement errors in income can exaggerate attenuation bias
The study investigates:
How teacher quality influences student performance.
Whether students adjust course selection behavior based on past grading experiences.
How to properly estimate teacher fixed effects while addressing selection bias and measurement error.
The initial model estimates student performance (Tijct) based on class expectations and student characteristics:
Tijct=α0+Sjctα1+Xijctα2+uijct
where:
Tijct = Student test score.
Sjct = Class-level grading expectation (e.g., expected GPA in the course).
Xijct = Individual student characteristics.
i = Student, j = Instructor, c = Course, t = Time.
uijct = Idiosyncratic error term.
A key issue in this model is that grading expectations may not be randomly assigned. If students select into courses based on grading expectations, simultaneity bias can arise.
To control for instructor and course heterogeneity, the model introduces teacher-course fixed effects (μjc):
Tijct=β0+Sjctβ1+Xijctβ2+μjc+ϵijct
where:
μjc is a unique fixed effect for each instructor-course combination.
This controls for instructor-specific grading policies and course difficulty.
It differs from a simple instructor effect (θj) and course effect (δc) because it captures interaction effects.
Implications of Instructor-Course Fixed Effects
Identification Strategy
A key challenge in estimating teacher effects is endogeneity from:
To address these concerns, the model first controls for observable teacher characteristics:
Yijt=Xitβ1+Teacher Experiencejtβ2+Teacher Educationjtβ3+Teacher Scoreitβ4+⋯+ϵijt
However, if teacher characteristics are correlated with unobserved ability, we replace them with teacher fixed effects:
Yijt=Xitα+Γitθj+uijt
where:
θj = Teacher Fixed Effect, capturing all time-invariant teacher characteristics.
Γit represents within-teacher variation.
To further analyze teacher impact, we express student test scores as:
Yijt=Xitγ+ϵijt
where:
γ represents the between and within variation.
eijt is the prediction error.
Decomposing the error term:
eijt=Titδj+˜eijt
where:
δj = Group-level teacher effect.
˜eijt = Residual error.
To control for prior student performance, we introduce lagged test scores:
Yijkt=Yijkt−1+Xitβ+Titτj+(Wi+Pk+ϵijkt)
where:
Yijkt−1 = Lagged student test score.
τj = Teacher Fixed Effect.
Wi = Student Fixed Effect.
Pk = School Fixed Effect.
uijkt=Wi+Pk+ϵijkt.
A major issue is selection bias:
If students sort into better teachers, the teacher effect (τ) may be overestimated.
Bias in τ for teacher j is:
1NjNj∑i=1(Wi+Pk+ϵijkt)
If teachers switch schools, we can separately estimate:
Teacher Fixed Effects (τj)
School Fixed Effects (Pk)
The mobility web refers to the network of teacher transitions across schools, which helps in identifying both teacher and school fixed effects.
Thin mobility web: Few teachers switch schools, making it harder to separate teacher effects from school effects.
Thick mobility web: Many teachers switch schools, improving identification of teacher quality independent of school characteristics.
The panel data model capturing student performance over time is:
Yijkt=Yijk(t−1)α+Xitβ+Titτ+Pk+ϵijkt
where:
Yijkt = Student performance at time t.
Yijk(t−1) = Lagged student test score.
Xit = Student characteristics.
Tit = Teacher effect (τ).
Pk = School fixed effect.
ϵijkt = Idiosyncratic error term.
If we apply fixed effects (demeaning transformation):
Yijkt−ˉYijk=(Xit−ˉXi)β+(Tit−ˉTi)τ+(Pk−ˉP)+(ϵijkt−ˉϵijk)
The paper argues that controlling for school fixed effects (Pk) ensures no selection bias, meaning students are randomly assigned within schools.
A key claim in the paper is that teacher quality (τ) does not depend on the number of students per teacher (Nj).
To test this, we examine the variance of estimated teacher effects:
var(τ)
If:
var(τ)=0
this implies teacher quality does not impact student performance.
To empirically test this, the study analyzes:
1NjNj∑i=1ϵijkt
which represents teacher-level average residuals.
Key Finding:
The variance of teacher effects remains stable across different class sizes (Nj).
This suggests that random assignment of students across teachers is not biasing τ.
Since teacher effects (τj) are estimated with error (Spin-off of Measurement Error), we decompose them as:
ˆτj=τj+λj
where:
τj = True teacher effect.
λj = Measurement error (e.g., sampling error, estimation noise).
Assuming τj and λj are uncorrelated:
cov(τj,λj)=0
this means that the randomness in student assignments does not systematically bias teacher quality estimates.
The total observed variance in estimated teacher effects is:
var(ˆτ)=var(τ)+var(λ)
Rearranging:
var(τ)=var(ˆτ)−var(λ)
Since we observe var(ˆτ), we need to estimate var(λ).
Measurement error variance (var(λ)) can be approximated using the average squared standard error of teacher effects:
var(λ)=1JJ∑j=1ˆσ2j
where ˆσ2j is the squared standard error of teacher j (which depends on sample size Nj).
The signal-to-noise ratio (or reliability) of teacher effect estimates is:
var(τ)var(ˆτ)=Reliability
where:
Higher reliability indicates that most of the variation comes from true teacher effects (τ) rather than noise.
Lower reliability suggests that a large portion of variation is due to measurement error.
The proportion of error variance in estimated teacher effects is:
1−var(τ)var(ˆτ)=Noise
Even if true teacher quality depends on class size (Nj), our method for estimating λ remains unaffected.
To check whether teacher effects are biased by sampling error, we regress estimated teacher effects (ˆτj) on teacher characteristics (Xj):
ˆτj=β0+Xjβ1+ϵj
If teacher characteristics do not predict sampling error, then:
R2≈0
This would confirm that teacher characteristics are uncorrelated with measurement error, validating the identification strategy.
We typically don’t test heteroskedasticity explicitly because robust covariance matrix estimation is used. However, other key assumptions should be tested before choosing the appropriate panel model.
library("plm")
data("EmplUK", package="plm")
data("Produc", package="plm")
data("Grunfeld", package="plm")
data("Wages", package="plm")Tests whether coefficients are the same across individuals (also known as an F-test of stability or Chow test).
H0: All individuals have the same coefficients (i.e., equal coefficients for all individuals).
Ha: Different individuals have different coefficients.
Notes:
A fixed effects model assumes different intercepts per individual.
A random effects model assumes a common intercept.
library(plm)
plm::pooltest(inv ~ value + capital,
data = Grunfeld,
model = "within")
#>
#> F statistic
#>
#> data: inv ~ value + capital
#> F = 5.7805, df1 = 18, df2 = 170, p-value = 1.219e-10
#> alternative hypothesis: unstabilityIf the null is rejected, we should not use a pooled OLS model.
Checks for the presence of individual or time effects, or both.
Types of tests:
honda: Default test for individual effects (Honda 1985)
bp: Breusch-Pagan test for unbalanced panels (Breusch and Pagan 1980)
kw: King-Wu test for unbalanced panels with two-way effects (M. L. King and Wu 1997)
ghm: Gourieroux, Holly, and Monfort test for two-way effects (Gourieroux, Holly, and Monfort 1982)
pFtest(inv ~ value + capital,
data = Grunfeld,
effect = "twoways")
#>
#> F test for twoways effects
#>
#> data: inv ~ value + capital
#> F = 17.403, df1 = 28, df2 = 169, p-value < 2.2e-16
#> alternative hypothesis: significant effects
pFtest(inv ~ value + capital,
data = Grunfeld,
effect = "individual")
#>
#> F test for individual effects
#>
#> data: inv ~ value + capital
#> F = 49.177, df1 = 9, df2 = 188, p-value < 2.2e-16
#> alternative hypothesis: significant effects
pFtest(inv ~ value + capital,
data = Grunfeld,
effect = "time")
#>
#> F test for time effects
#>
#> data: inv ~ value + capital
#> F = 0.23451, df1 = 19, df2 = 178, p-value = 0.9997
#> alternative hypothesis: significant effectsIf the null hypothesis is rejected, a fixed effects model is more appropriate.
Tests whether residuals across entities are correlated.
pcdtest(inv ~ value + capital,
data = Grunfeld, model = "within")
#>
#> Pesaran CD test for cross-sectional dependence in panels
#>
#> data: inv ~ value + capital
#> z = 4.6612, p-value = 3.144e-06
#> alternative hypothesis: cross-sectional dependenceUses a spatial weight matrix w.
pcdtest(inv ~ value + capital,
data = Grunfeld,
model = "within",
w = weight_matrix)If the null is rejected, cross-sectional correlation exists and should be addressed.
Types of Serial Correlation Tests
library(plm)
data("Produc", package = "plm")
# Wooldridge test for unobserved individual effects
pwtest(log(gsp) ~ log(pcap) + log(pc) + log(emp) + unemp,
data = Produc)
#>
#> Wooldridge's test for unobserved individual effects
#>
#> data: formula
#> z = 3.9383, p-value = 8.207e-05
#> alternative hypothesis: unobserved effectInterpretation: If we reject H0, pooled OLS is inappropriate due to the presence of unobserved effects.
Joint LM Test for Random Effects and Serial Correlation
A Lagrange Multiplier test to jointly detect:
Null Hypothesis: Normality and homoskedasticity of idiosyncratic errors (Baltagi and Li 1991, 1995).
# Baltagi and Li's joint test for serial correlation and random effects
pbsytest(log(gsp) ~ log(pcap) + log(pc) + log(emp) + unemp,
data = Produc,
test = "j")
#>
#> Baltagi and Li AR-RE joint test
#>
#> data: formula
#> chisq = 4187.6, df = 2, p-value < 2.2e-16
#> alternative hypothesis: AR(1) errors or random effectsInterpretation: If we reject H0, either serial correlation, random effects, or both are present. But we don’t know the source of dependence.
To distinguish the source of dependence, we use either (both tests assume normality and homoskedasticity) (Bera, Sosa-Escudero, and Yoon 2001):
BSY Test for Serial Correlation
pbsytest(log(gsp) ~ log(pcap) + log(pc) + log(emp) + unemp,
data = Produc)
#>
#> Bera, Sosa-Escudero and Yoon locally robust test
#>
#> data: formula
#> chisq = 52.636, df = 1, p-value = 4.015e-13
#> alternative hypothesis: AR(1) errors sub random effectsBSY Test for Random Effects
pbsytest(log(gsp) ~ log(pcap) + log(pc) + log(emp) + unemp,
data = Produc,
test = "re")
#>
#> Bera, Sosa-Escudero and Yoon locally robust test (one-sided)
#>
#> data: formula
#> z = 57.914, p-value < 2.2e-16
#> alternative hypothesis: random effects sub AR(1) errorsIf serial correlation is “known” to be absent (based on the BSY test), the LM test for random effects is superior.
plmtest(inv ~ value + capital,
data = Grunfeld,
type = "honda")
#>
#> Lagrange Multiplier Test - (Honda)
#>
#> data: inv ~ value + capital
#> normal = 28.252, p-value < 2.2e-16
#> alternative hypothesis: significant effectsIf random effects are absent (based on the BSY test), we use Breusch-Godfrey’s serial correlation test (Breusch 1978; Godfrey 1978).
lmtest::bgtest()If Random Effects are Present: Use Baltagi and Li’s Test
Baltagi and Li’s test detects serial correlation in AR(1) and MA(1) processes under random effects.
Null hypothesis (H0): Uncorrelated errors.
Note:
The test has power only against positive serial correlation (one-sided).
It is applicable only to balanced panels
Applicable to random effects, pooled OLS, and fixed effects models.
Can test for higher-order serial correlation.
# Baltagi-Griffin test for higher-order serial correlation
plm::pbgtest(plm::plm(inv ~ value + capital,
data = Grunfeld,
model = "within"),
order = 2)
#>
#> Breusch-Godfrey/Wooldridge test for serial correlation in panel models
#>
#> data: inv ~ value + capital
#> chisq = 42.587, df = 2, p-value = 5.655e-10
#> alternative hypothesis: serial correlation in idiosyncratic errorsFor short panels (Small T, Large N), use Wooldridge’s test:
library(tseries)
# Example: Test for unit root in GDP data
adf.test(Produc$gsp, alternative = "stationary")
#>
#> Augmented Dickey-Fuller Test
#>
#> data: Produc$gsp
#> Dickey-Fuller = -6.5425, Lag order = 9, p-value = 0.01
#> alternative hypothesis: stationaryIf we reject H0, the series is stationary and does not exhibit a stochastic trend.
library(tseries)
library(plm)
# Levin-Lin-Chu (LLC) Unit Root Test
purtest(Grunfeld, test = "levinlin")
#>
#> Levin-Lin-Chu Unit-Root Test (ex. var.: None)
#>
#> data: Grunfeld
#> z = 0.39906, p-value = 0.6551
#> alternative hypothesis: stationarityIf we reject H0, the series is stationary.
Purpose: Detects heteroskedasticity in regression residuals.
Null hypothesis (H0): The data is homoskedastic (constant variance).
Alternative hypothesis (HA): The data exhibits heteroskedasticity (non-constant variance).
Decision Rule:
If the p-value is small (e.g., p<0.05), reject H0, suggesting heteroskedasticity.
If the p-value is large (p≥0.05), fail to reject H0, implying homoskedasticity.
library(lmtest)
# Fit a panel model (pooled OLS)
model <- lm(log(gsp) ~ log(pcap) + log(pc) + log(emp) + unemp,
data = Produc)
# Breusch-Pagan Test for Heteroskedasticity
bptest(model)
#>
#> studentized Breusch-Pagan test
#>
#> data: model
#> BP = 80.033, df = 4, p-value < 2.2e-16If heteroskedasticity is detected, we need to adjust for it using robust standard errors.
If heteroskedasticity is present, robust covariance matrix estimation is recommended. Different estimators apply depending on whether serial correlation is also an issue.
Choosing the Correct Robust Covariance Matrix Estimator
| Estimator | Corrects for Heteroskedasticity? | Corrects for Serial Correlation? | Recommended For |
|---|---|---|---|
"white1" |
✅ Yes | ❌ No | Random Effects |
"white2" |
✅ Yes (common variance within groups) | ❌ No | Random Effects |
"arellano" |
✅ Yes | ✅ Yes | Fixed Effects |
library(plm)
# Fit a fixed effects model
fe_model <- plm(log(gsp) ~ log(pcap) + log(pc) + log(emp) + unemp,
data = Produc,
model = "within")
# Compute robust standard errors using Arellano's method
coeftest(fe_model, vcov = vcovHC(fe_model, method = "arellano"))
#>
#> t test of coefficients:
#>
#> Estimate Std. Error t value Pr(>|t|)
#> log(pcap) -0.0261497 0.0603262 -0.4335 0.66480
#> log(pc) 0.2920069 0.0617425 4.7294 2.681e-06 ***
#> log(emp) 0.7681595 0.0816652 9.4062 < 2.2e-16 ***
#> unemp -0.0052977 0.0024958 -2.1226 0.03411 *
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Using a robust covariance matrix corrects for heteroskedasticity and/or serial correlation, ensuring valid inference.
Panel data models must be chosen based on the structure of the data and underlying assumptions. This section provides guidance on selecting between Pooled OLS, Random Effects, and Fixed Effects models.
The choice between POLS and RE depends on whether there are unobserved individual effects.
Breusch-Pagan Lagrange Multiplier Test
library(plm)
# Breusch-Pagan LM Test
plmtest(plm(inv ~ value + capital, data = Grunfeld,
model = "pooling"), type = "bp")
#>
#> Lagrange Multiplier Test - (Breusch-Pagan)
#>
#> data: inv ~ value + capital
#> chisq = 798.16, df = 1, p-value < 2.2e-16
#> alternative hypothesis: significant effectsIf the test is significant, RE is more appropriate than POLS.
The choice between FE and RE depends on whether the individual-specific effects are correlated with the regressors.
Key Assumptions and Properties
| Hypothesis | If True |
|---|---|
| H0:Cov(ci,xit)=0 | ˆβRE is consistent and efficient, while ˆβFE is consistent |
| H0:Cov(ci,xit)≠0 | ˆβRE is inconsistent, while ˆβFE remains consistent |
Hausman Test
For the Hausman test to work, you need to assume that
Then,
If p<0.05: Reject H0, meaning FE is preferred.
If p≥0.05: Fail to reject H0, meaning RE can be used.
library(plm)
# Fit FE and RE models
fe_model <- plm(inv ~ value + capital, data = Grunfeld, model = "within")
re_model <- plm(inv ~ value + capital, data = Grunfeld, model = "random")
# Hausman test
phtest(fe_model, re_model)
#>
#> Hausman Test
#>
#> data: inv ~ value + capital
#> chisq = 2.3304, df = 2, p-value = 0.3119
#> alternative hypothesis: one model is inconsistentIf the null hypothesis is rejected, use FE. If not, RE is appropriate.
All three estimators (POLS, RE, FE) require:
However, additional assumptions determine whether the estimator is consistent and efficient.
POLS
Consistent if:
A3a Exogeneity holds: E(x′ituit)=0
RE assumption holds: E(x′itci)=0
If A4 Homoskedasticity does not hold: Use cluster-robust standard errors, but POLS is not efficient.
RE
Consistent if:
A3a Exogeneity holds: E(x′ituit)=0
RE assumption holds: E(x′itci)=0
If A4 Homoskedasticity holds: RE is most efficient.
If A4 Homoskedasticity does not hold: Use cluster-robust standard errors. RE remains more efficient than POLS but is not the most efficient.
FE
Consistent if:
Limitations:
Cannot estimate the effects of time-constant variables.
A4 Homoskedasticity generally does not hold, so cluster-robust SEs are required.
Estimator Selection Guide
| Estimator / True Model | POLS | RE | FE |
|---|---|---|---|
| POLS | ✅ Consistent | ✅ Consistent | ❌ Inconsistent |
| FE | ✅ Consistent | ✅ Consistent | ✅ Consistent |
| RE | ✅ Consistent | ✅ Consistent | ❌ Inconsistent |
Other estimators are available depending on model violations and additional considerations:
Violation Estimators: Adjust for assumption violations.
Basic Estimators: Standard POLS, RE, FE.
Instrumental Variable Estimator: Used for endogeneity.
Variable Coefficient Estimator: Allows varying coefficients.
Generalized Method of Moments Estimator: For dynamic panel models.
General Feasible GLS Estimator: Accounts for heteroskedasticity and serial correlation.
Means Groups Estimator: Averages individual-specific estimates.
Common Correlated Effects Mean Group Estimator: Accounts for cross-sectional dependence.
Limited Dependent Variable Estimators: Used for binary or censored data.
plm Package
The plm package in R is designed for panel data analysis, allowing users to estimate various models, including pooled OLS, fixed effects, random effects, and other specifications commonly used in econometrics.
For a detailed guide, refer to:
The official vignette on plm functions.
# Load the package
library("plm")
data("Produc", package = "plm")
# Display first few rows
head(Produc)
#> state year region pcap hwy water util pc gsp emp
#> 1 ALABAMA 1970 6 15032.67 7325.80 1655.68 6051.20 35793.80 28418 1010.5
#> 2 ALABAMA 1971 6 15501.94 7525.94 1721.02 6254.98 37299.91 29375 1021.9
#> 3 ALABAMA 1972 6 15972.41 7765.42 1764.75 6442.23 38670.30 31303 1072.3
#> 4 ALABAMA 1973 6 16406.26 7907.66 1742.41 6756.19 40084.01 33430 1135.5
#> 5 ALABAMA 1974 6 16762.67 8025.52 1734.85 7002.29 42057.31 33749 1169.8
#> 6 ALABAMA 1975 6 17316.26 8158.23 1752.27 7405.76 43971.71 33604 1155.4
#> unemp
#> 1 4.7
#> 2 5.2
#> 3 4.7
#> 4 3.9
#> 5 5.5
#> 6 7.7To specify panel data, we define the individual (cross-sectional) and time identifiers:
# Convert data to panel format
pdata <- pdata.frame(Produc, index = c("state", "year"))
# Check structure
summary(pdata)
#> state year region pcap hwy
#> ALABAMA : 17 1970 : 48 5 :136 Min. : 2627 Min. : 1827
#> ARIZONA : 17 1971 : 48 8 :136 1st Qu.: 7097 1st Qu.: 3858
#> ARKANSAS : 17 1972 : 48 4 :119 Median : 17572 Median : 7556
#> CALIFORNIA : 17 1973 : 48 1 :102 Mean : 25037 Mean :10218
#> COLORADO : 17 1974 : 48 3 : 85 3rd Qu.: 27692 3rd Qu.:11267
#> CONNECTICUT: 17 1975 : 48 6 : 68 Max. :140217 Max. :47699
#> (Other) :714 (Other):528 (Other):170
#> water util pc gsp
#> Min. : 228.5 Min. : 538.5 Min. : 4053 Min. : 4354
#> 1st Qu.: 764.5 1st Qu.: 2488.3 1st Qu.: 21651 1st Qu.: 16503
#> Median : 2266.5 Median : 7008.8 Median : 40671 Median : 39987
#> Mean : 3618.8 Mean :11199.5 Mean : 58188 Mean : 61014
#> 3rd Qu.: 4318.7 3rd Qu.:11598.5 3rd Qu.: 64796 3rd Qu.: 68126
#> Max. :24592.3 Max. :80728.1 Max. :375342 Max. :464550
#>
#> emp unemp
#> Min. : 108.3 Min. : 2.800
#> 1st Qu.: 475.0 1st Qu.: 5.000
#> Median : 1164.8 Median : 6.200
#> Mean : 1747.1 Mean : 6.602
#> 3rd Qu.: 2114.1 3rd Qu.: 7.900
#> Max. :11258.0 Max. :18.000
#> The plm package allows for the estimation of several different panel data models.
A simple pooled OLS model assumes a common intercept and ignores individual-specific effects.
pooling <- plm(log(gsp) ~ log(pcap) + log(emp) + unemp,
data = pdata,
model = "pooling")
summary(pooling)
#> Pooling Model
#>
#> Call:
#> plm(formula = log(gsp) ~ log(pcap) + log(emp) + unemp, data = pdata,
#> model = "pooling")
#>
#> Balanced Panel: n = 48, T = 17, N = 816
#>
#> Residuals:
#> Min. 1st Qu. Median 3rd Qu. Max.
#> -0.302260 -0.085204 -0.018166 0.051783 0.500144
#>
#> Coefficients:
#> Estimate Std. Error t-value Pr(>|t|)
#> (Intercept) 2.2124123 0.0790988 27.9703 < 2e-16 ***
#> log(pcap) 0.4121307 0.0216314 19.0525 < 2e-16 ***
#> log(emp) 0.6205834 0.0199495 31.1078 < 2e-16 ***
#> unemp -0.0035444 0.0020539 -1.7257 0.08478 .
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Total Sum of Squares: 849.81
#> Residual Sum of Squares: 13.326
#> R-Squared: 0.98432
#> Adj. R-Squared: 0.98426
#> F-statistic: 16990.2 on 3 and 812 DF, p-value: < 2.22e-16This estimator takes the average over time for each entity, reducing within-group variation.
between <- plm(log(gsp) ~ log(pcap) + log(emp) + unemp,
data = pdata, model = "between")
summary(between)
#> Oneway (individual) effect Between Model
#>
#> Call:
#> plm(formula = log(gsp) ~ log(pcap) + log(emp) + unemp, data = pdata,
#> model = "between")
#>
#> Balanced Panel: n = 48, T = 17, N = 816
#> Observations used in estimation: 48
#>
#> Residuals:
#> Min. 1st Qu. Median 3rd Qu. Max.
#> -0.172055 -0.086456 -0.013203 0.038100 0.394336
#>
#> Coefficients:
#> Estimate Std. Error t-value Pr(>|t|)
#> (Intercept) 2.0784403 0.3277756 6.3410 1.063e-07 ***
#> log(pcap) 0.4585009 0.0892620 5.1366 6.134e-06 ***
#> log(emp) 0.5751005 0.0828921 6.9379 1.410e-08 ***
#> unemp -0.0031585 0.0145683 -0.2168 0.8294
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Total Sum of Squares: 48.875
#> Residual Sum of Squares: 0.65861
#> R-Squared: 0.98652
#> Adj. R-Squared: 0.98561
#> F-statistic: 1073.73 on 3 and 44 DF, p-value: < 2.22e-16The first-differences model eliminates time-invariant effects by differencing adjacent periods.
firstdiff <- plm(log(gsp) ~ log(pcap) + log(emp) + unemp,
data = pdata, model = "fd")
summary(firstdiff)
#> Oneway (individual) effect First-Difference Model
#>
#> Call:
#> plm(formula = log(gsp) ~ log(pcap) + log(emp) + unemp, data = pdata,
#> model = "fd")
#>
#> Balanced Panel: n = 48, T = 17, N = 816
#> Observations used in estimation: 768
#>
#> Residuals:
#> Min. 1st Qu. Median 3rd Qu. Max.
#> -0.0846921 -0.0108511 0.0016861 0.0124968 0.1018911
#>
#> Coefficients:
#> Estimate Std. Error t-value Pr(>|t|)
#> (Intercept) 0.0101353 0.0013206 7.6749 5.058e-14 ***
#> log(pcap) -0.0167634 0.0453958 -0.3693 0.712
#> log(emp) 0.8212694 0.0362737 22.6409 < 2.2e-16 ***
#> unemp -0.0061615 0.0007516 -8.1978 1.032e-15 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Total Sum of Squares: 1.0802
#> Residual Sum of Squares: 0.33394
#> R-Squared: 0.69086
#> Adj. R-Squared: 0.68965
#> F-statistic: 569.123 on 3 and 764 DF, p-value: < 2.22e-16Controls for time-invariant heterogeneity by demeaning data within individuals.
fixed <- plm(log(gsp) ~ log(pcap) + log(emp) + unemp,
data = pdata, model = "within")
summary(fixed)
#> Oneway (individual) effect Within Model
#>
#> Call:
#> plm(formula = log(gsp) ~ log(pcap) + log(emp) + unemp, data = pdata,
#> model = "within")
#>
#> Balanced Panel: n = 48, T = 17, N = 816
#>
#> Residuals:
#> Min. 1st Qu. Median 3rd Qu. Max.
#> -0.1253873 -0.0248746 -0.0054276 0.0184698 0.2026394
#>
#> Coefficients:
#> Estimate Std. Error t-value Pr(>|t|)
#> log(pcap) 0.03488447 0.03092191 1.1281 0.2596
#> log(emp) 1.03017988 0.02161353 47.6636 <2e-16 ***
#> unemp -0.00021084 0.00096121 -0.2194 0.8264
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Total Sum of Squares: 18.941
#> Residual Sum of Squares: 1.3077
#> R-Squared: 0.93096
#> Adj. R-Squared: 0.92645
#> F-statistic: 3438.48 on 3 and 765 DF, p-value: < 2.22e-16Accounts for unobserved heterogeneity by modeling it as a random component.
random <- plm(log(gsp) ~ log(pcap) + log(emp) + unemp,
data = pdata, model = "random")
summary(random)
#> Oneway (individual) effect Random Effect Model
#> (Swamy-Arora's transformation)
#>
#> Call:
#> plm(formula = log(gsp) ~ log(pcap) + log(emp) + unemp, data = pdata,
#> model = "random")
#>
#> Balanced Panel: n = 48, T = 17, N = 816
#>
#> Effects:
#> var std.dev share
#> idiosyncratic 0.001709 0.041345 0.103
#> individual 0.014868 0.121934 0.897
#> theta: 0.918
#>
#> Residuals:
#> Min. 1st Qu. Median 3rd Qu. Max.
#> -0.1246674 -0.0268273 -0.0049657 0.0214145 0.2389889
#>
#> Coefficients:
#> Estimate Std. Error z-value Pr(>|z|)
#> (Intercept) 3.10569727 0.14715985 21.1042 <2e-16 ***
#> log(pcap) 0.03708054 0.02747015 1.3498 0.1771
#> log(emp) 1.00937552 0.02103951 47.9752 <2e-16 ***
#> unemp 0.00004806 0.00092301 0.0521 0.9585
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Total Sum of Squares: 24.523
#> Residual Sum of Squares: 1.4425
#> R-Squared: 0.94118
#> Adj. R-Squared: 0.94096
#> Chisq: 12992.5 on 3 DF, p-value: < 2.22e-16Model Selection and Diagnostic Tests
The Breusch-Pagan LM test compares random effects with pooled OLS.
Null Hypothesis: OLS is preferred.
Alternative Hypothesis: Random effects model is appropriate.
plmtest(pooling, effect = "individual", type = "bp")
#>
#> Lagrange Multiplier Test - (Breusch-Pagan)
#>
#> data: log(gsp) ~ log(pcap) + log(emp) + unemp
#> chisq = 4567.1, df = 1, p-value < 2.2e-16
#> alternative hypothesis: significant effectsOther test types: "honda", "kw", "ghm". Other effects: "time", "twoways".
Breusch-Pagan LM test for cross-sectional dependence
pcdtest(fixed, test = "lm")
#>
#> Breusch-Pagan LM test for cross-sectional dependence in panels
#>
#> data: log(gsp) ~ log(pcap) + log(emp) + unemp
#> chisq = 6490.4, df = 1128, p-value < 2.2e-16
#> alternative hypothesis: cross-sectional dependencePesaran’s CD statistic
pcdtest(fixed, test = "cd")
#>
#> Pesaran CD test for cross-sectional dependence in panels
#>
#> data: log(gsp) ~ log(pcap) + log(emp) + unemp
#> z = 37.13, p-value < 2.2e-16
#> alternative hypothesis: cross-sectional dependenceUsed to check for autocorrelation in panel data.
pbgtest(fixed)
#>
#> Breusch-Godfrey/Wooldridge test for serial correlation in panel models
#>
#> data: log(gsp) ~ log(pcap) + log(emp) + unemp
#> chisq = 476.92, df = 17, p-value < 2.2e-16
#> alternative hypothesis: serial correlation in idiosyncratic errorsChecks whether a time series variable is stationary.
library(tseries)
adf.test(pdata$gsp, k = 2)
#>
#> Augmented Dickey-Fuller Test
#>
#> data: pdata$gsp
#> Dickey-Fuller = -5.9028, Lag order = 2, p-value = 0.01
#> alternative hypothesis: stationaryNull Hypothesis: Pooled OLS is appropriate.
Alternative Hypothesis: Fixed effects model is preferred.
pFtest(fixed, pooling)
#>
#> F test for individual effects
#>
#> data: log(gsp) ~ log(pcap) + log(emp) + unemp
#> F = 149.58, df1 = 47, df2 = 765, p-value < 2.2e-16
#> alternative hypothesis: significant effectsNull Hypothesis: Random effects are appropriate.
Alternative Hypothesis: Fixed effects are preferred (RE assumptions are violated).
phtest(random, fixed)
#>
#> Hausman Test
#>
#> data: log(gsp) ~ log(pcap) + log(emp) + unemp
#> chisq = 84.924, df = 3, p-value < 2.2e-16
#> alternative hypothesis: one model is inconsistentHeteroskedasticity and Robust Standard Errors
Tests whether heteroskedasticity is present in the panel dataset.
library(lmtest)
bptest(log(gsp) ~ log(pcap) + log(emp) + unemp, data = pdata)
#>
#> studentized Breusch-Pagan test
#>
#> data: log(gsp) ~ log(pcap) + log(emp) + unemp
#> BP = 98.223, df = 3, p-value < 2.2e-16If heteroskedasticity is detected, use robust standard errors:
For Random Effects Model
# Original coefficients
coeftest(random)
#>
#> t test of coefficients:
#>
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 3.10569727 0.14715985 21.1042 <2e-16 ***
#> log(pcap) 0.03708054 0.02747015 1.3498 0.1774
#> log(emp) 1.00937552 0.02103951 47.9752 <2e-16 ***
#> unemp 0.00004806 0.00092301 0.0521 0.9585
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# Heteroskedasticity-consistent standard errors
coeftest(random, vcovHC)
#>
#> t test of coefficients:
#>
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 3.10569727 0.23261788 13.3511 <2e-16 ***
#> log(pcap) 0.03708054 0.06125725 0.6053 0.5451
#> log(emp) 1.00937552 0.06395880 15.7817 <2e-16 ***
#> unemp 0.00004806 0.00215219 0.0223 0.9822
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# Different HC types
t(sapply(c("HC0", "HC1", "HC2", "HC3", "HC4"), function(x)
sqrt(diag(vcovHC(random, type = x)))
))
#> (Intercept) log(pcap) log(emp) unemp
#> HC0 0.2326179 0.06125725 0.06395880 0.002152189
#> HC1 0.2331901 0.06140795 0.06411614 0.002157484
#> HC2 0.2334857 0.06161618 0.06439057 0.002160392
#> HC3 0.2343595 0.06197939 0.06482756 0.002168646
#> HC4 0.2342815 0.06235576 0.06537813 0.002168867HC0: Default heteroskedasticity-consistent (White’s estimator).
HC1, HC2, HC3: Recommended for small samples.
HC4: Useful for small samples with influential observations.
For Fixed Effects Model
# Original coefficients
coeftest(fixed)
#>
#> t test of coefficients:
#>
#> Estimate Std. Error t value Pr(>|t|)
#> log(pcap) 0.03488447 0.03092191 1.1281 0.2596
#> log(emp) 1.03017988 0.02161353 47.6636 <2e-16 ***
#> unemp -0.00021084 0.00096121 -0.2194 0.8264
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# Heteroskedasticity-consistent standard errors
coeftest(fixed, vcovHC)
#>
#> t test of coefficients:
#>
#> Estimate Std. Error t value Pr(>|t|)
#> log(pcap) 0.03488447 0.06661083 0.5237 0.6006
#> log(emp) 1.03017988 0.06413365 16.0630 <2e-16 ***
#> unemp -0.00021084 0.00217453 -0.0970 0.9228
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# Arellano method for robust errors
coeftest(fixed, vcovHC(fixed, method = "arellano"))
#>
#> t test of coefficients:
#>
#> Estimate Std. Error t value Pr(>|t|)
#> log(pcap) 0.03488447 0.06661083 0.5237 0.6006
#> log(emp) 1.03017988 0.06413365 16.0630 <2e-16 ***
#> unemp -0.00021084 0.00217453 -0.0970 0.9228
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# Different HC types
t(sapply(c("HC0", "HC1", "HC2", "HC3", "HC4"), function(x)
sqrt(diag(vcovHC(fixed, type = x)))
))
#> log(pcap) log(emp) unemp
#> HC0 0.06661083 0.06413365 0.002174525
#> HC1 0.06673362 0.06425187 0.002178534
#> HC2 0.06689078 0.06441024 0.002182114
#> HC3 0.06717278 0.06468886 0.002189747
#> HC4 0.06742431 0.06496436 0.002193150| Test | Null Hypothesis (H₀) | Decision Rule |
|---|---|---|
| LM Test | OLS is appropriate | Reject H₀ → Use RE |
| Hausman Test | Random effects preferred | Reject H₀ → Use FE |
| pFtest | OLS is appropriate | Reject H₀ → Use FE |
| Breusch-Pagan | No heteroskedasticity | Reject H₀ → Use robust SE |
Variance Components Structure
Beyond the standard random effects model, the plm package provides additional methods for estimating variance components models and instrumental variable techniques for dealing with endogeneity in panel data.
Different estimators for the variance components structure exist in the literature, and plm allows users to specify them through the random.method argument.
Random Effects Estimators:
"swar" (default): Swamy and Arora estimator (Swamy and Arora 1972).
"walhus": Wallace and Hussain estimator (Wallace and Hussain 1969).
"amemiya": Amemiya estimator (Amemiya 1971).
"nerlove": Nerlove estimator (Nerlove 1971) (Note: Not available for two-way random effects).
Effects in Panel Models:
Individual effects (default).
Time effects (effect = "time").
Two-way effects (effect = "twoways").
amemiya <- plm(
log(gsp) ~ log(pcap) + log(emp) + unemp,
data = pdata,
model = "random",
random.method = "amemiya",
effect = "twoways"
)
summary(amemiya)
#> Twoways effects Random Effect Model
#> (Amemiya's transformation)
#>
#> Call:
#> plm(formula = log(gsp) ~ log(pcap) + log(emp) + unemp, data = pdata,
#> effect = "twoways", model = "random", random.method = "amemiya")
#>
#> Balanced Panel: n = 48, T = 17, N = 816
#>
#> Effects:
#> var std.dev share
#> idiosyncratic 0.001228 0.035039 0.028
#> individual 0.041201 0.202981 0.941
#> time 0.001359 0.036859 0.031
#> theta: 0.9582 (id) 0.8641 (time) 0.8622 (total)
#>
#> Residuals:
#> Min. 1st Qu. Median 3rd Qu. Max.
#> -0.13796209 -0.01951506 -0.00053384 0.01807398 0.20452581
#>
#> Coefficients:
#> Estimate Std. Error z-value Pr(>|z|)
#> (Intercept) 3.9581876 0.1767036 22.4001 < 2.2e-16 ***
#> log(pcap) 0.0378443 0.0253963 1.4902 0.136184
#> log(emp) 0.8891887 0.0227677 39.0548 < 2.2e-16 ***
#> unemp -0.0031568 0.0011240 -2.8086 0.004976 **
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Total Sum of Squares: 5.3265
#> Residual Sum of Squares: 0.98398
#> R-Squared: 0.81527
#> Adj. R-Squared: 0.81458
#> Chisq: 3583.53 on 3 DF, p-value: < 2.22e-16The ercomp() function retrieves estimates of the variance components in a random effects model. Below, we extract the variance decomposition using Amemiya’s method:
ercomp(log(gsp) ~ log(pcap) + log(emp) + unemp,
data = pdata,
method = "amemiya",
effect = "twoways")
#> var std.dev share
#> idiosyncratic 0.001228 0.035039 0.028
#> individual 0.041201 0.202981 0.941
#> time 0.001359 0.036859 0.031
#> theta: 0.9582 (id) 0.8641 (time) 0.8622 (total)This output includes:
Variance of the individual effect.
Variance of the time effect (if applicable).
Variance of the idiosyncratic error.
Checking Panel Data Balance
Panel datasets may be balanced (each individual has observations for all time periods) or unbalanced (some individuals are missing observations). The punbalancedness() function measures the degree of balance in the data, with values closer to 1 indicating a balanced panel (Ahrens and Pincus 1981).
punbalancedness(random)
#> gamma nu
#> 1 1Instrumental Variables in Panel Data
Instrumental variables (IV) are used to address endogeneity, which arises when regressors are correlated with the error term. plm provides various IV estimation methods through the inst.method argument.
Instrumental Variable Estimators
"bvk": Balestra-Varadharajan-Krishnakumar estimator (default) (Balestra and Varadharajan-Krishnakumar 1987).
"baltagi": Baltagi estimator (Baltagi 1981).
"am": Amemiya-MaCurdy estimator (Amemiya and MaCurdy 1986).
"bms": Breusch-Mizon-Schmidt estimator (Breusch, Mizon, and Schmidt 1989).
Other Estimators in Panel Data Models
Beyond standard fixed effects and random effects models, the plm package provides additional estimation techniques tailored for heterogeneous coefficients, dynamic panel models, and feasible generalized least squares (FGLS) methods.
Variable Coefficients Model (pvcm)
The variable coefficients model (VCM) allows coefficients to vary across cross-sectional units, accounting for unobserved heterogeneity more flexibly.
Two Estimation Approaches:
Fixed effects (within): Assumes coefficients are constant over time but vary across individuals.
Random effects (random): Assumes coefficients are drawn from a random distribution.
fixed_pvcm <-
pvcm(log(gsp) ~ log(pcap) + log(emp) + unemp,
data = pdata,
model = "within")
random_pvcm <-
pvcm(log(gsp) ~ log(pcap) + log(emp) + unemp,
data = pdata,
model = "random")
summary(fixed_pvcm)
#> Oneway (individual) effect No-pooling model
#>
#> Call:
#> pvcm(formula = log(gsp) ~ log(pcap) + log(emp) + unemp, data = pdata,
#> model = "within")
#>
#> Balanced Panel: n = 48, T = 17, N = 816
#>
#> Residuals:
#> Min. 1st Qu. Median 3rd Qu. Max.
#> -0.075247625 -0.013247956 0.000666934 0.013852996 0.118966807
#>
#> Coefficients:
#> (Intercept) log(pcap) log(emp) unemp
#> Min. :-3.8868 Min. :-1.11962 Min. :0.3790 Min. :-1.597e-02
#> 1st Qu.: 0.9917 1st Qu.:-0.38475 1st Qu.:0.8197 1st Qu.:-5.319e-03
#> Median : 2.9848 Median :-0.03147 Median :1.1506 Median : 5.335e-05
#> Mean : 2.8079 Mean :-0.06028 Mean :1.1656 Mean : 9.024e-04
#> 3rd Qu.: 4.3553 3rd Qu.: 0.25573 3rd Qu.:1.3779 3rd Qu.: 8.374e-03
#> Max. :12.8800 Max. : 1.16922 Max. :2.4276 Max. : 2.507e-02
#>
#> Total Sum of Squares: 15729
#> Residual Sum of Squares: 0.40484
#> Multiple R-Squared: 0.99997
summary(random_pvcm)
#> Oneway (individual) effect Random coefficients model
#>
#> Call:
#> pvcm(formula = log(gsp) ~ log(pcap) + log(emp) + unemp, data = pdata,
#> model = "random")
#>
#> Balanced Panel: n = 48, T = 17, N = 816
#>
#> Residuals:
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> -0.23364 -0.03401 0.05558 0.09811 0.19349 1.14326
#>
#> Estimated mean of the coefficients:
#> Estimate Std. Error z-value Pr(>|z|)
#> (Intercept) 2.79030044 0.53104167 5.2544 1.485e-07 ***
#> log(pcap) -0.04195768 0.08621579 -0.4867 0.6265
#> log(emp) 1.14988911 0.07225221 15.9149 < 2.2e-16 ***
#> unemp 0.00031135 0.00163864 0.1900 0.8493
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Estimated variance of the coefficients:
#> (Intercept) log(pcap) log(emp) unemp
#> (Intercept) 11.2648882 -1.335932 0.2035824 0.00827707
#> log(pcap) -1.3359322 0.287021 -0.1872915 -0.00345298
#> log(emp) 0.2035824 -0.187291 0.2134845 0.00336374
#> unemp 0.0082771 -0.003453 0.0033637 0.00009425
#>
#> Total Sum of Squares: 15729
#> Residual Sum of Squares: 40.789
#> Multiple R-Squared: 0.99741
#> Chisq: 739.334 on 3 DF, p-value: < 2.22e-16
#> Test for parameter homogeneity: Chisq = 21768.8 on 188 DF, p-value: < 2.22e-16Generalized Method of Moments Estimator (pgmm)
The Generalized Method of Moments estimator is commonly used for dynamic panel models, especially when:
There is concern over endogeneity in lagged dependent variables.
Instrumental variables are used for estimation.
library(plm)
# estimates a dynamic labor demand function using one-step GMM,
# applying lagged variables as instruments
z2 <- pgmm(
log(emp) ~ lag(log(emp), 1) + lag(log(wage), 0:1) +
lag(log(capital), 0:1) |
lag(log(emp), 2:99) +
lag(log(wage), 2:99) + lag(log(capital), 2:99),
data = EmplUK,
effect = "twoways",
model = "onestep",
transformation = "ld"
)
summary(z2, robust = TRUE)
#> Twoways effects One-step model System GMM
#>
#> Call:
#> pgmm(formula = log(emp) ~ lag(log(emp), 1) + lag(log(wage), 0:1) +
#> lag(log(capital), 0:1) | lag(log(emp), 2:99) + lag(log(wage),
#> 2:99) + lag(log(capital), 2:99), data = EmplUK, effect = "twoways",
#> model = "onestep", transformation = "ld")
#>
#> Unbalanced Panel: n = 140, T = 7-9, N = 1031
#>
#> Number of Observations Used: 1642
#> Residuals:
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> -0.7530341 -0.0369030 0.0000000 0.0002882 0.0466069 0.6001503
#>
#> Coefficients:
#> Estimate Std. Error z-value Pr(>|z|)
#> lag(log(emp), 1) 0.935605 0.026295 35.5810 < 2.2e-16 ***
#> lag(log(wage), 0:1)0 -0.630976 0.118054 -5.3448 9.050e-08 ***
#> lag(log(wage), 0:1)1 0.482620 0.136887 3.5257 0.0004224 ***
#> lag(log(capital), 0:1)0 0.483930 0.053867 8.9838 < 2.2e-16 ***
#> lag(log(capital), 0:1)1 -0.424393 0.058479 -7.2572 3.952e-13 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Sargan test: chisq(100) = 118.763 (p-value = 0.097096)
#> Autocorrelation test (1): normal = -4.808434 (p-value = 1.5212e-06)
#> Autocorrelation test (2): normal = -0.2800133 (p-value = 0.77947)
#> Wald test for coefficients: chisq(5) = 11174.82 (p-value = < 2.22e-16)
#> Wald test for time dummies: chisq(7) = 14.71138 (p-value = 0.039882)Explanation of Arguments:
log(emp) ~ lag(log(emp), 1) + lag(log(wage), 0:1) + lag(log(capital), 0:1)
→ Specifies the dynamic model, where log(emp) depends on its first lag and contemporaneous plus lagged values of log(wage) and log(capital).
| lag(log(emp), 2:99) + lag(log(wage), 2:99) + lag(log(capital), 2:99)
→ Instruments for endogenous regressors, using further lags.
effect = "twoways"
→ Includes both individual and time effects.
model = "onestep"
→ Uses one-step GMM (alternative: "twostep" for efficiency gain).
transformation = "ld"
→ Uses lagged differences as transformation.
Generalized Feasible Generalized Least Squares Models (pggls)
The FGLS estimator (pggls) is robust against:
Intragroup heteroskedasticity.
Serial correlation (within groups).
However, it assumes no cross-sectional correlation and is most suitable when NNN (cross-sectional units) is much larger than TTT (time periods), i.e., long panels.
Random Effects FGLS Model:
zz <- pggls(
log(emp) ~ log(wage) + log(capital),
data = EmplUK,
model = "pooling"
)
summary(zz)
#> Oneway (individual) effect General FGLS model
#>
#> Call:
#> pggls(formula = log(emp) ~ log(wage) + log(capital), data = EmplUK,
#> model = "pooling")
#>
#> Unbalanced Panel: n = 140, T = 7-9, N = 1031
#>
#> Residuals:
#> Min. 1st Qu. Median Mean 3rd Qu. Max.
#> -1.80696 -0.36552 0.06181 0.03230 0.44279 1.58719
#>
#> Coefficients:
#> Estimate Std. Error z-value Pr(>|z|)
#> (Intercept) 2.023480 0.158468 12.7690 < 2.2e-16 ***
#> log(wage) -0.232329 0.048001 -4.8401 1.298e-06 ***
#> log(capital) 0.610484 0.017434 35.0174 < 2.2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> Total Sum of Squares: 1853.6
#> Residual Sum of Squares: 402.55
#> Multiple R-squared: 0.78283Fixed Effects FGLS Model:
zz <- pggls(
log(emp) ~ log(wage) + log(capital),
data = EmplUK,
model = "within"
)
summary(zz)
#> Oneway (individual) effect Within FGLS model
#>
#> Call:
#> pggls(formula = log(emp) ~ log(wage) + log(capital), data = EmplUK,
#> model = "within")
#>
#> Unbalanced Panel: n = 140, T = 7-9, N = 1031
#>
#> Residuals:
#> Min. 1st Qu. Median 3rd Qu. Max.
#> -0.508362414 -0.074254395 -0.002442181 0.076139063 0.601442300
#>
#> Coefficients:
#> Estimate Std. Error z-value Pr(>|z|)
#> log(wage) -0.617617 0.030794 -20.056 < 2.2e-16 ***
#> log(capital) 0.561049 0.017185 32.648 < 2.2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> Total Sum of Squares: 1853.6
#> Residual Sum of Squares: 17.368
#> Multiple R-squared: 0.99063Key Considerations:
Efficient under the assumption of homoskedasticity.
Inefficient if there is group-wise heteroskedasticity.
Ideal for large-N, small-T panels.
| Estimator | Method | Application |
|---|---|---|
Variable Coefficients (pvcm) |
Fixed (within), Random (random) |
Allows coefficients to vary across individuals. |
GMM (pgmm) |
One-step, Two-step | Used in dynamic models with endogeneity. |
Feasible GLS (pggls) |
Fixed (within), Random (pooling) |
Handles heteroskedasticity and serial correlation but assumes no cross-sectional correlation. |
fixest Package
The fixest package provides efficient and flexible methods for estimating fixed effects and generalized linear models in panel data. It is optimized for handling large datasets with high-dimensional fixed effects and allows for multiple model estimation, robust standard errors, and split-sample estimation.
For further details, refer to the official fixest vignette.
Available Estimation Functions in fixest
| Function | Model Type |
|---|---|
feols |
Fixed effects OLS (linear regression) |
feglm |
Generalized linear models (GLMs) |
femlm |
Maximum likelihood estimation (MLE) |
feNmlm |
Non-linear models (non-linear in RHS parameters) |
fepois |
Poisson fixed-effects regression |
fenegbin |
Negative binomial fixed-effects regression |
Note: These functions work only for
fixestobjects.
library(fixest)
data(airquality)
# Setting a variable dictionary for output labeling
setFixest_dict(
c(
Ozone = "Ozone (ppb)",
Solar.R = "Solar Radiation (Langleys)",
Wind = "Wind Speed (mph)",
Temp = "Temperature"
)
)
# Fixed effects OLS with stepwise estimation and clustering
est <- feols(
Ozone ~ Solar.R + sw0(Wind + Temp) | csw(Month, Day),
data = airquality,
cluster = ~ Day
)
# Display results
etable(est)
#> est.1 est.2
#> Dependent Var.: Ozone (ppb) Ozone (ppb)
#>
#> Solar Radiation (Langleys) 0.1148*** (0.0234) 0.0522* (0.0202)
#> Wind Speed (mph) -3.109*** (0.7986)
#> Temperature 1.875*** (0.3671)
#> Fixed-Effects: ------------------ ------------------
#> Month Yes Yes
#> Day No No
#> __________________________ __________________ __________________
#> S.E.: Clustered by: Day by: Day
#> Observations 111 111
#> R2 0.31974 0.63686
#> Within R2 0.12245 0.53154
#>
#> est.3 est.4
#> Dependent Var.: Ozone (ppb) Ozone (ppb)
#>
#> Solar Radiation (Langleys) 0.1078** (0.0329) 0.0509* (0.0236)
#> Wind Speed (mph) -3.289*** (0.7777)
#> Temperature 2.052*** (0.2415)
#> Fixed-Effects: ----------------- ------------------
#> Month Yes Yes
#> Day Yes Yes
#> __________________________ _________________ __________________
#> S.E.: Clustered by: Day by: Day
#> Observations 111 111
#> R2 0.58018 0.81604
#> Within R2 0.12074 0.61471
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# Output in LaTeX format
etable(est, tex = TRUE)
#> \begingroup
#> \centering
#> \begin{tabular}{lcccc}
#> \tabularnewline \midrule \midrule
#> Dependent Variable: & \multicolumn{4}{c}{Ozone (ppb)}\\
#> Model: & (1) & (2) & (3) & (4)\\
#> \midrule
#> \emph{Variables}\\
#> Solar Radiation (Langleys) & 0.1148$^{***}$ & 0.0522$^{**}$ & 0.1078$^{***}$ & 0.0509$^{**}$\\
#> & (0.0234) & (0.0202) & (0.0329) & (0.0236)\\
#> Wind Speed (mph) & & -3.109$^{***}$ & & -3.289$^{***}$\\
#> & & (0.7986) & & (0.7777)\\
#> Temperature & & 1.875$^{***}$ & & 2.052$^{***}$\\
#> & & (0.3671) & & (0.2415)\\
#> \midrule
#> \emph{Fixed-effects}\\
#> Month & Yes & Yes & Yes & Yes\\
#> Day & & & Yes & Yes\\
#> \midrule
#> \emph{Fit statistics}\\
#> Observations & 111 & 111 & 111 & 111\\
#> R$^2$ & 0.31974 & 0.63686 & 0.58018 & 0.81604\\
#> Within R$^2$ & 0.12245 & 0.53154 & 0.12074 & 0.61471\\
#> \midrule \midrule
#> \multicolumn{5}{l}{\emph{Clustered (Day) standard-errors in parentheses}}\\
#> \multicolumn{5}{l}{\emph{Signif. Codes: ***: 0.01, **: 0.05, *: 0.1}}\\
#> \end{tabular}
#> \par\endgroup
# Extract fixed-effects coefficients
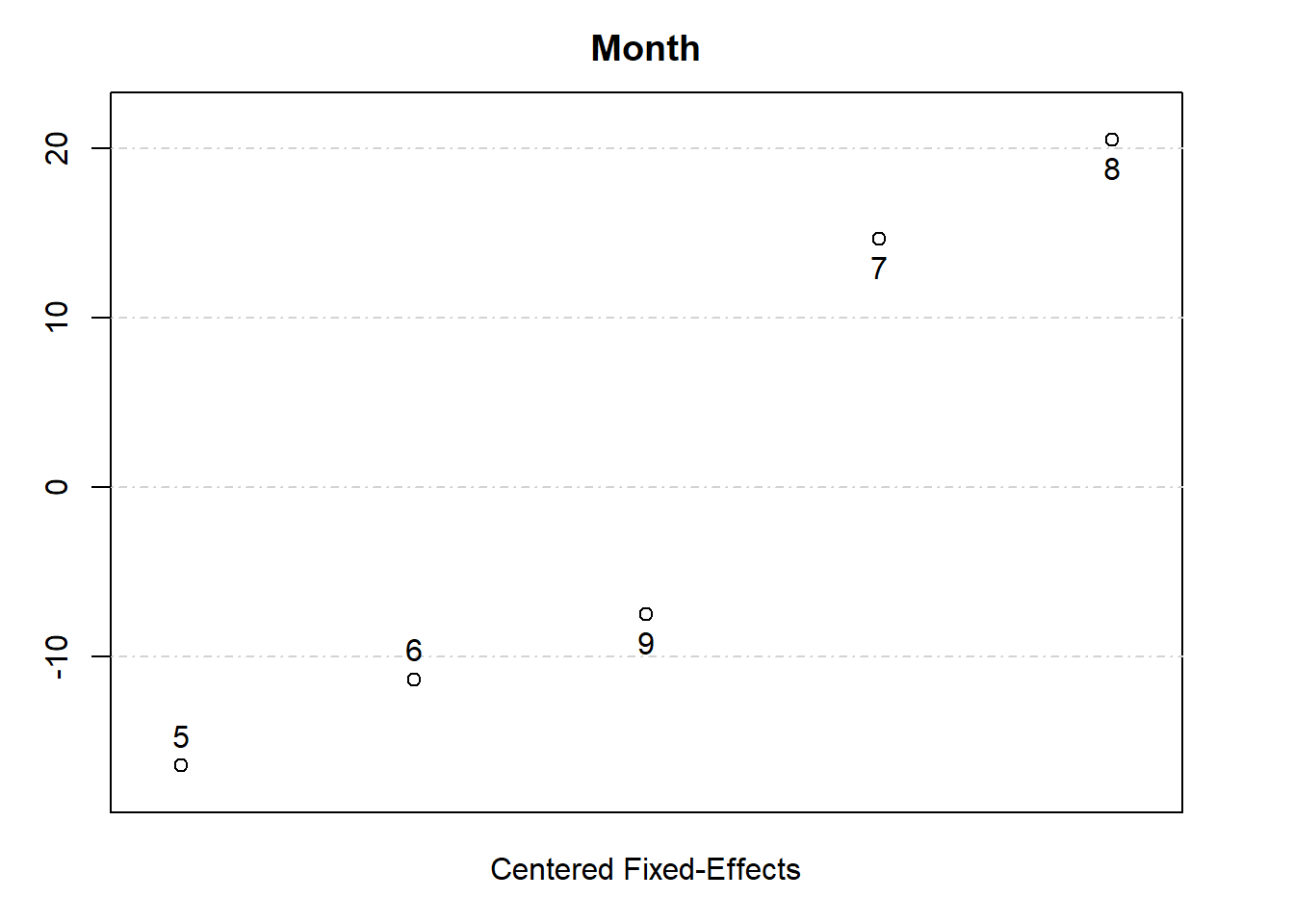
fixedEffects <- fixef(est[[1]])
summary(fixedEffects)
#> Fixed_effects coefficients
#> Number of fixed-effects for variable Month is 5.
#> Mean = 19.6 Variance = 272
#>
#> COEFFICIENTS:
#> Month: 5 6 7 8 9
#> 3.219 8.288 34.26 40.12 12.13
# View fixed effects for one dimension
fixedEffects$Month
#> 5 6 7 8 9
#> 3.218876 8.287899 34.260812 40.122257 12.130971
# Plot fixed effects
plot(fixedEffects)
This example demonstrates:
Fixed effects estimation (| csw(Month, Day)).
Stepwise selection (sw0(Wind + Temp)).
Clustering of standard errors (cluster = ~ Day).
Extracting and plotting fixed effects.
Multiple Model Estimation
Use feols() to estimate models with multiple dependent variables simultaneously:
etable(feols(c(Sepal.Length, Sepal.Width) ~
Petal.Length + Petal.Width,
data = iris))
#> feols(c(Sepal.L..1 feols(c(Sepal.Le..2
#> Dependent Var.: Sepal.Length Sepal.Width
#>
#> Constant 4.191*** (0.0970) 3.587*** (0.0937)
#> Petal.Length 0.5418*** (0.0693) -0.2571*** (0.0669)
#> Petal.Width -0.3196* (0.1605) 0.3640* (0.1550)
#> _______________ __________________ ___________________
#> S.E. type IID IID
#> Observations 150 150
#> R2 0.76626 0.21310
#> Adj. R2 0.76308 0.20240
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Alternatively, define a list of dependent variables and loop over them:
depvars <- c("Sepal.Length", "Sepal.Width")
res <- lapply(depvars, function(var) {
feols(xpd(..lhs ~ Petal.Length + Petal.Width, ..lhs = var), data = iris)
})
etable(res)
#> model 1 model 2
#> Dependent Var.: Sepal.Length Sepal.Width
#>
#> Constant 4.191*** (0.0970) 3.587*** (0.0937)
#> Petal.Length 0.5418*** (0.0693) -0.2571*** (0.0669)
#> Petal.Width -0.3196* (0.1605) 0.3640* (0.1550)
#> _______________ __________________ ___________________
#> S.E. type IID IID
#> Observations 150 150
#> R2 0.76626 0.21310
#> Adj. R2 0.76308 0.20240
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Use stepwise functions to estimate different model specifications efficiently.
Options to write the functions
sw (stepwise): sequentially analyze each elements
y ~ sw(x1, x2) will be estimated as y ~ x1 and y ~ x2
sw0 (stepwise 0): similar to sw but also estimate a model without the elements in the set first
y ~ sw(x1, x2) will be estimated as y ~ 1 and y ~ x1 and y ~ x2
csw (cumulative stepwise): sequentially add each element of the set to the formula
y ~ csw(x1, x2) will be estimated as y ~ x1 and y ~ x1 + x2
csw0 (cumulative stepwise 0): similar to csw but also estimate a model without the elements in the set first
y ~ csw(x1, x2) will be estimated as y~ 1 y ~ x1 and y ~ x1 + x2
mvsw (multiverse stepwise): all possible combination of the elements in the set (it will get large very quick).
mvsw(x1, x2, x3) will be sw0(x1, x2, x3, x1 + x2, x1 + x3, x2 + x3, x1 + x2 + x3)
| Stepwise Function | Description |
|---|---|
sw(x1, x2) |
Sequentially estimates models with each element separately. |
sw0(x1, x2) |
Same as sw(), but also estimates a baseline model without the elements. |
csw(x1, x2) |
Sequentially adds each element to the formula. |
csw0(x1, x2) |
Same as csw(), but also includes a baseline model. |
mvsw(x1, x2, x3) |
Estimates all possible combinations of the variables. |
# Example: Cumulative Stepwise Estimation
etable(feols(Ozone ~ csw(Solar.R, Wind, Temp), data = airquality))
#> feols(Ozone ~ c..1 feols(Ozone ~ c..2
#> Dependent Var.: Ozone (ppb) Ozone (ppb)
#>
#> Constant 18.60** (6.748) 77.25*** (9.068)
#> Solar Radiation (Langleys) 0.1272*** (0.0328) 0.1004*** (0.0263)
#> Wind Speed (mph) -5.402*** (0.6732)
#> Temperature
#> __________________________ __________________ __________________
#> S.E. type IID IID
#> Observations 111 111
#> R2 0.12134 0.44949
#> Adj. R2 0.11328 0.43930
#>
#> feols(Ozone ~ c..3
#> Dependent Var.: Ozone (ppb)
#>
#> Constant -64.34** (23.05)
#> Solar Radiation (Langleys) 0.0598* (0.0232)
#> Wind Speed (mph) -3.334*** (0.6544)
#> Temperature 1.652*** (0.2535)
#> __________________________ __________________
#> S.E. type IID
#> Observations 111
#> R2 0.60589
#> Adj. R2 0.59484
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Split-Sample Estimation
Estimate separate regressions for different subgroups in the dataset using fsplit.
etable(feols(Ozone ~ Solar.R + Wind, fsplit = ~ Month, data = airquality))
#> feols(Ozone ~ S..1 feols(Ozone ..2 feols(Ozone ~..3
#> Sample (Month) Full sample 5 6
#> Dependent Var.: Ozone (ppb) Ozone (ppb) Ozone (ppb)
#>
#> Constant 77.25*** (9.068) 50.55* (18.30) 8.997 (16.83)
#> Solar Radiation (Langleys) 0.1004*** (0.0263) 0.0294 (0.0379) 0.1518. (0.0676)
#> Wind Speed (mph) -5.402*** (0.6732) -2.762* (1.300) -0.6177 (1.674)
#> __________________________ __________________ _______________ ________________
#> S.E. type IID IID IID
#> Observations 111 24 9
#> R2 0.44949 0.22543 0.52593
#> Adj. R2 0.43930 0.15166 0.36790
#>
#> feols(Ozone ~ ..4 feols(Ozone ~ ..5
#> Sample (Month) 7 8
#> Dependent Var.: Ozone (ppb) Ozone (ppb)
#>
#> Constant 88.39*** (20.81) 95.76*** (19.83)
#> Solar Radiation (Langleys) 0.1135. (0.0582) 0.2146** (0.0654)
#> Wind Speed (mph) -6.319*** (1.559) -8.228*** (1.528)
#> __________________________ _________________ _________________
#> S.E. type IID IID
#> Observations 26 23
#> R2 0.52423 0.70640
#> Adj. R2 0.48286 0.67704
#>
#> feols(Ozone ~ ..6
#> Sample (Month) 9
#> Dependent Var.: Ozone (ppb)
#>
#> Constant 67.10*** (14.35)
#> Solar Radiation (Langleys) 0.0373 (0.0463)
#> Wind Speed (mph) -4.161*** (1.071)
#> __________________________ _________________
#> S.E. type IID
#> Observations 29
#> R2 0.38792
#> Adj. R2 0.34084
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1This estimates models separately for each Month in the dataset.
Robust Standard Errors in fixest
fixest supports a variety of robust standard error estimators, including:
iid: errors are homoskedastic and independent and identically distributed
hetero: errors are heteroskedastic using White correction
cluster: errors are correlated within the cluster groups
newey_west: (Newey and West 1986) use for time series or panel data. Errors are heteroskedastic and serially correlated.
vcov = newey_west ~ id + period where id is the subject id and period is time period of the panel.
to specify lag period to consider vcov = newey_west(2) ~ id + period where we’re considering 2 lag periods.
driscoll_kraay (Driscoll and Kraay 1998) use for panel data. Errors are cross-sectionally and serially correlated.
vcov = discoll_kraay ~ periodconley: (Conley 1999) for cross-section data. Errors are spatially correlated
vcov = conley ~ latitude + longitude
to specify the distance cutoff, vcov = vcov_conley(lat = "lat", lon = "long", cutoff = 100, distance = "spherical"), which will use the conley() helper function.
hc: from the sandwich package
vcov = function(x) sandwich::vcovHC(x, type = "HC1"))To let R know which SE estimation you want to use, insert vcov = vcov_type ~ variables
Example: Newey-West Standard Errors
etable(feols(
Ozone ~ Solar.R + Wind,
data = airquality,
vcov = newey_west ~ Month + Day
))
#> feols(Ozone ~ So..
#> Dependent Var.: Ozone (ppb)
#>
#> Constant 77.25*** (10.03)
#> Solar Radiation (Langleys) 0.1004*** (0.0258)
#> Wind Speed (mph) -5.402*** (0.8353)
#> __________________________ __________________
#> S.E. type Newey-West (L=2)
#> Observations 111
#> R2 0.44949
#> Adj. R2 0.43930
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Specify the number of lag periods to consider:
etable(feols(
Ozone ~ Solar.R + Wind,
data = airquality,
vcov = newey_west(2) ~ Month + Day
))
#> feols(Ozone ~ So..
#> Dependent Var.: Ozone (ppb)
#>
#> Constant 77.25*** (10.03)
#> Solar Radiation (Langleys) 0.1004*** (0.0258)
#> Wind Speed (mph) -5.402*** (0.8353)
#> __________________________ __________________
#> S.E. type Newey-West (L=2)
#> Observations 111
#> R2 0.44949
#> Adj. R2 0.43930
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Conley Spatial Correlation: vcov = conley ~ latitude + longitude
To specify a distance cutoff: vcov = vcov_conley(lat = "lat", lon = "long", cutoff = 100, distance = "spherical")
Using Standard Errors from the sandwich Package
etable(feols(
Ozone ~ Solar.R + Wind,
data = airquality,
vcov = function(x)
sandwich::vcovHC(x, type = "HC1")
))
#> feols(Ozone ~ So..
#> Dependent Var.: Ozone (ppb)
#>
#> Constant 77.25*** (9.590)
#> Solar Radiation (Langleys) 0.1004*** (0.0231)
#> Wind Speed (mph) -5.402*** (0.8134)
#> __________________________ __________________
#> S.E. type vcovHC(type="HC1")
#> Observations 111
#> R2 0.44949
#> Adj. R2 0.43930
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Small Sample Correction
Apply small sample adjustments using ssc():
etable(feols(
Ozone ~ Solar.R + Wind,
data = airquality,
ssc = ssc(adj = TRUE, cluster.adj = TRUE)
))
#> feols(Ozone ~ So..
#> Dependent Var.: Ozone (ppb)
#>
#> Constant 77.25*** (9.068)
#> Solar Radiation (Langleys) 0.1004*** (0.0263)
#> Wind Speed (mph) -5.402*** (0.6732)
#> __________________________ __________________
#> S.E. type IID
#> Observations 111
#> R2 0.44949
#> Adj. R2 0.43930
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1This corrects for bias when working with small samples.
Selecting the appropriate data type depends on:
Research Questions: Do you need to understand changes over time at the individual level (panel) or just a snapshot comparison at one point (cross-sectional)?
Resources: Longitudinal or panel studies can be resource-intensive.
Time Constraints: If you need fast results, cross-sectional or repeated cross-sectional might be more practical.
Analytical Goals: Time-series forecasting, causal inference, or descriptive comparison each has different data requirements.
Availability: Sometimes only secondary or repeated cross-sectional data is available, which constrains the design.
Regardless of data type, data quality is crucial. Poor data—be it incomplete, biased, or improperly measured—can lead to incorrect conclusions. Researchers should:
Ensure Validity and Reliability: Use well-designed instruments and consistent measurement techniques.
Address Missing Data: Apply appropriate imputation methods if feasible.
Manage Attrition (in Panel Data): Consider weighting or sensitivity analyses to deal with dropouts.
Check Representativeness: Especially in cross-sectional and repeated cross-sectional surveys, ensure sampling frames match the target population.
Protect Confidentiality and Privacy: Particularly in panel studies with repeated contact, store data securely and follow ethical guidelines.
Obtain Proper Consent: Inform participants about study details, usage of data, and rights to withdraw.