27 Regression Discontinuity
Causal inference often requires creativity when randomized experiments are impractical, unethical, or too costly. In such situations, researchers turn to quasi-experimental designs that mimic the structure of randomized experiments under certain assumptions. One of the most compelling and rigorous among these is the Regression Discontinuity (RD) design, a method that turns a seemingly arbitrary policy rule into an opportunity for causal estimation.
Imagine a policy in which financial aid is awarded only to students whose family income falls below a certain threshold, or a marketing campaign targeted solely at customers with a credit score above a specified value. These cutoffs create a situation where treatment assignment hinges on a single continuous variable (e.g., income or credit score ) crossing a fixed boundary. This boundary, or cutoff, introduces a discrete change in treatment probability based on a smooth, underlying score. That is the central insight behind RD: when individuals just above and just below the threshold are otherwise similar, comparing their outcomes offers a window into local average treatment effects.
The RD design exploits this structure by focusing on the “edge” (the region near the cutoff) where treatment assignment changes abruptly. While units far from the threshold may differ systematically, those close to it are assumed to be comparable, as if randomly assigned to treatment or control. This gives RD a compelling advantage: under relatively mild assumptions, it can deliver credible causal estimates, particularly in situations where randomized controlled trials (RCTs) are infeasible.
Originally introduced by Thistlethwaite and Campbell (1960) in their evaluation of merit-based scholarships and their impact on academic outcomes, RD has since evolved into a widely used econometric tool across fields such as education, healthcare, marketing, political science, and finance. Its theoretical foundation was significantly refined and extended in modern work by G. Imbens and Lemieux (2008) and Lee and Lemieux (2010), who formalized its assumptions and estimation strategies.
RD designs come in two primary flavors:
Sharp RD, where the treatment assignment is perfectly determined by whether the running variable exceeds the cutoff.
Fuzzy RD, where the probability of treatment changes discontinuously at the cutoff but is not deterministically assigned.
In either case, the defining characteristic is the discontinuity in the treatment assignment rule based on a continuous score, often referred to as the running variable, forcing variable, or assignment variable.
Regression Discontinuity offers a powerful yet intuitive approach to causal inference, particularly when treatment assignment rules are rigid and known. In the sections that follow, we will develop the formal framework of RD designs, examine the key assumptions that underlie their validity, and apply the method to real-world business and policy problems.
27.1 Conceptual Framework
To truly appreciate the logic of RD designs, one must think like an experimentalist, but with observational data. RD transforms a deterministic rule (e.g., a policy cutoff) into an opportunity for quasi-random assignment. It is, in essence, a localized experiment conducted at the threshold of a continuous running variable.
At the heart of the RD framework is a deceptively simple idea: individuals just above and just below the cutoff are virtually identical in all respects, except for the treatment status induced by their position relative to the threshold. This intuition enables RD designs to estimate causal effects with high internal validity, even in the absence of random assignment.
RD’s strength lies in its focus on a narrow window around the cutoff, often called the bandwidth, where the assumption of exchangeability is most plausible. Within this narrow range, the assignment mechanism approximates a randomized experiment.
- Internal Validity: Extremely strong near the cutoff. The closer the observations are to the threshold, the more credible the assumption that they are otherwise comparable.
- External Validity: More limited. Estimates are local to the cutoff and may not generalize to units far from the threshold. This tradeoff between precision and generalizability is a defining characteristic of RD.
One of the most compelling validations of RD comes from empirical comparisons with randomized controlled trials (RCTs). Evidence from studies such as Chaplin et al. (2018) and Gleason, Resch, and Berk (2018) suggest that RD and RCTs often yield remarkably similar treatment effect estimates, underscoring RD’s credibility when its assumptions are met. While RD is not a substitute for randomization, it can come surprisingly close in practice.
RD is not an island; it shares conceptual and methodological links with several other causal inference frameworks. Understanding these connections helps clarify when RD is appropriate and how it complements alternative approaches.
- Randomized Experiment: RD can be seen as a local randomization design (treatment is “as-if” randomly assigned near the cutoff).
- Instrumental Variables: RD can be framed as a special case of a structural IV model (J. D. Angrist and Lavy 1999), where the running variable induces exogenous variation in treatment at the threshold.
- Matching Methods: RD resembles a highly targeted form of matching (matching units just above and below a single threshold) (J. J. Heckman, LaLonde, and Smith 1999).
- Interrupted Time Series (ITS): RD outperforms ITS when the running variable is finely measured and continuous. However, in settings with highly discrete or temporally aggregated data (e.g., quarterly revenues or annual crime rates), ITS may be more suitable. Still, when the data are dense or effectively continuous, RD offers a more precise and defensible design.
27.2 Types of Regression Discontinuity Designs
RD is not a one-size-fits-all approach. While the classic setup involves a binary treatment determined by a threshold-crossing rule, numerous extensions and variants exist, each tailored to different research contexts. Understanding these variations is essential for choosing the appropriate design and interpreting results correctly.
-
Sharp RD: The simplest and most intuitive form of RD:
- Definition: Treatment assignment jumps deterministically from 0 to 1 at the cutoff.
- Implication: Individuals below the threshold are never treated; those above always are.
- Identification: The treatment effect is identified as the jump in the outcome at the cutoff.
- Example: A scholarship awarded strictly to students with test scores ≥ 85.
-
Fuzzy RD: A generalization of the sharp design:
- Definition: The probability of treatment increases discontinuously at the cutoff, but does not jump from 0 to 1.
- Implication: Some individuals below the cutoff may receive the treatment, and some above may not.
- Identification: Requires instrumental variable methods to estimate the local average treatment effects (LATE) for compliers.
- Example: A healthcare subsidy that is more likely, but not guaranteed, to be received by patients above a certain income level.
-
Kink RD: A subtler variant based on a change in slope:
- Definition: The first derivative (slope) of the outcome changes at the cutoff, rather than its level.
- Identification: The treatment effect is identified from a discontinuity in the marginal effect of the running variable.
- Example: Tax incentives where the marginal benefit changes at a threshold income level.
- References: See theoretical foundations in (Card et al. 2015) and empirical applications in (Böckerman, Kanninen, and Suoniemi 2018; Nielsen, Sørensen, and Taber 2010).
- Regression Discontinuity in Time (RDiT): Also known as a special case of Interrupted Time Series:
- Definition: The running variable is time, and the cutoff corresponds to a policy implementation date or event.
- Application: Evaluates the immediate impact of an intervention that begins at a known point in time.
- Caveat: Since time trends are often confounded by other events, careful modeling of pre- and post-trends is essential.
Note: RDiT is often less reliable than traditional RD due to potential violations of the continuity assumption, especially when time is measured in coarse intervals (e.g., quarterly or yearly).
RD designs have been extended in several directions to accommodate real-world complexities:
-
Multiple Cutoffs:
- Use case: Different treatment thresholds apply to different subgroups (e.g., age groups, regions).
- Challenge: Requires careful pooling and stratification to maintain comparability.
-
Multiple Scores (Multiple Running Variables):
- Use case: Treatment depends on more than one score (e.g., income and age).
- Approach: Involves multivariate threshold rules or interaction effects.
- Geographic RD (Spatial RD):
- Definition: The cutoff is defined in space, such as administrative borders or policy boundaries.
- Example: A tax policy that applies only to businesses within a specific jurisdiction.
- Dynamic Treatments:
- Definition: Treatment effects may evolve over time after the initial intervention.
- Consideration: Requires longitudinal data and appropriate modeling of lagged effects.
- Continuous Treatment Intensity (Dose-Response RD):
- Definition: Instead of a binary treatment, units receive varying degrees of treatment intensity based on the running variable.
- Example: Advertising exposure that increases progressively with customer engagement scores.
27.2.1 Assumptions for RD Validity
Independent Assignment: The treatment is assigned solely based on the running variable.
-
Continuity of Conditional Expectations: The expected outcomes without treatment are continuous at the cutoff:
\[ E[Y(0)|X=x] \text{ and } E[Y(1)|X=x] \text{ are continuous at } x = c. \]
Exogeneity of the Cutoff: The cutoff should not be manipulable. No confounding interventions at the cutoff.
No Discontinuity in Confounding Variables: Other covariates should be smooth at the threshold. A common test is to check for jumps in covariates unrelated to treatment.
See Table 27.1 for examples of possible violations.
| Issue | Description | Solution |
|---|---|---|
| Violation of Continuity in Covariates | If other variables besides treatment exhibit a discontinuity at the cutoff, the estimated effect may be biased. | Conduct balance tests on pre-treatment covariates. |
| Multiple Discontinuities | When multiple threshold effects exist, identification becomes more challenging. | Use robustness checks with alternative model specifications. |
| Manipulation of the Running Variable | Subjects may manipulate \(X_i\) to qualify for treatment (e.g., strategic behavior in test scores). | Implement McCrary’s density test to check for discontinuities in the distribution of \(X_i\). |
27.3 Model Estimation Strategies
Under regression discontinuity framework, researchers can choose between parametric and nonparametric models. The choice depends on assumptions about functional form, data availability, and the trade-off between flexibility and interpretability.
27.3.1 Parametric Models: Polynomial Regression
Parametric models, such as linear regression, assume a specific functional form for the relationship between the dependent variable and predictors. One way to relax the strict linearity assumption is by incorporating polynomial functions of the forcing variable (Lee and Lemieux 2010). The choice of polynomial degree should be determined based on data characteristics.
However, using high-order polynomials comes with challenges. Gelman and Imbens (2019) highlight three key issues associated with global high-degree polynomials:
- Imprecise Estimates Due to Noise: Higher-degree polynomials can overfit, capturing noise instead of meaningful patterns.
- Sensitivity to Polynomial Degree: Estimates can vary significantly depending on the chosen degree, making the model less stable.
- Inadequate Confidence Interval Coverage: Confidence intervals tend to be misleading when using high-degree polynomials, leading to incorrect inference.
For these reasons, researchers are often advised to avoid global high-order polynomials and instead rely on alternative approaches (i.e., nonparametric version).
27.3.2 Nonparametric Models: Local Regression
Nonparametric models, such as local polynomial regression, offer greater flexibility by avoiding strong assumptions about functional form. Instead of fitting a single equation to the entire dataset, these methods estimate relationships locally, often using linear or quadratic polynomials within a neighborhood of each data point.
- Uses weighted observations near the cutoff.
- More flexible than global polynomial regression.
Local regression methods, such as local linear regression, address the shortcomings of high-order global polynomials by:
- Reducing overfitting, as they adapt to local patterns without excessive complexity.
- Providing stable estimates, since results are less sensitive to arbitrary choices of polynomial degree.
- Improving inference, ensuring more reliable confidence intervals.
By balancing flexibility and robustness, local regression techniques are often preferred over global polynomial models in applied research.
Best Practice: Use multiple model specifications to check for consistency in results.
27.4 Formal Definition
Let \(X_i\) be the running variable, \(c\) the cutoff, and \(D_i\) the treatment indicator:
\[ D_i = 1_{X_i > c} \]
or equivalently,
\[ D_i = \begin{cases} 1, & X_i > c \\ 0, & X_i < c \end{cases} \]
where:
\(D_i\): Treatment assignment
\(X_i\): Running variable (continuous)
\(c\): Cutoff value
27.4.1 Identification Assumptions
27.4.1.1 Continuity-Based Identification
RD estimates the [Local Average Treatment Effect] at the cutoff:
\[ \begin{aligned} \alpha_{SRDD} &= E[Y_{1i} - Y_{0i} | X_i = c] \\ &= E[Y_{1i}|X_i = c] - E[Y_{0i}|X_i = c] \\ &= \lim_{x \to c^+} E[Y_{1i}|X_i = x] - \lim_{x \to c^-} E[Y_{0i}|X_i = x] \end{aligned} \]
This relies on the assumption that, in the absence of treatment, the conditional expectation of potential outcomes is continuous at the threshold \(c\).
27.4.1.2 Local Randomization-Based Identification
Alternatively, identification can be achieved using local randomization within a small bandwidth \(W\) (i.e., a neighborhood around the cutoff). The [Local Average Treatment Effect] in this case is:
\[ \begin{aligned} \alpha_{LR} &= E[Y_{1i} - Y_{0i}|X_i \in W] \\ &= \frac{1}{N_1} \sum_{X_i \in W, D_i = 1} Y_i - \frac{1}{N_0} \sum_{X_i \in W, D_i = 0} Y_i \end{aligned} \]
Since RD estimates are local, they may not generalize to the entire population. However, for many applications, internal validity is of primary concern (rather than external validity).
27.5 Estimation and Inference
27.5.1 Local Randomization-Based Approach
The local randomization approach additionally assumes that within the chosen window \(W = [c - w, c + w]\), treatment assignment is as good as random. This requires:
- The joint probability distribution of running variable values inside \(W\) to be known.
- Potential outcomes to be independent of the running variable within \(W\).
This is a stronger assumption than continuity-based identification, as it requires that regression functions are smooth at \(c\) and remain unaffected by \(X_i\) within \(W\).
Since researchers can choose the window \(W\) (where random assignment plausibly holds), the sample size can often be small.
The selection of \(W\) can be based on:
- Pre-treatment covariate balance: Ensure covariates are similar across the threshold.
- Independent tests: Check for independence between the outcome and the running variable.
- Domain knowledge: Use theoretical or empirical justification for the window choice.
For inference, researchers can use:
- (Fisher) randomization inference
- (Neyman) design-based methods
27.5.2 Continuity-Based Approach
Also known as the local polynomial regression method, this approach estimates treatment effects by fitting a polynomial model locally around the cutoff. Global polynomial regression is not recommended due to issues such as:
- Lack of robustness
- Overfitting
- Runge’s phenomenon (oscillatory behavior at boundaries)
Steps for Local Polynomial Estimation
- Choose the polynomial order and weighting scheme
- Select an optimal bandwidth (minimizing MSE or coverage error)
- Estimate the parameter of interest
- Perform robust bias-corrected inference
This method ensures that estimation remains local, capturing the treatment effect precisely at the cutoff.
27.6 Specification Checks
To validate the credibility of an RD design, researchers perform several specification checks:
- Balance Checks
- Sorting, Bunching, and Manipulation
- Placebo Tests
- Sensitivity to Bandwidth Choice
- Manipulation-Robust Regression Discontinuity Bounds
27.6.1 Balance Checks
Also known as checking for discontinuities in average covariates, this test examines whether covariates that should not be affected by treatment exhibit a discontinuity at the cutoff.
- Null Hypothesis (\(H_0\)): The average effect of covariates on pseudo-outcomes (i.e., those that should not be influenced by treatment) is zero.
- If rejected, this raises serious doubts about the RD design, necessitating a strong justification.
27.6.2 Sorting, Bunching, and Manipulation
This test, also known as checking for discontinuities in the distribution of the forcing variable, detects whether subjects manipulate the running variable to sort into or out of treatment.
If individuals can manipulate the running variable, especially when the cutoff is known in advance, this can lead to bunching behavior (i.e., clustering just above or below the cutoff).
- If treatment is desirable, individuals will try to sort into treatment, leading to a gap just below the cutoff.
- If treatment is undesirable, individuals will try to avoid it, leading to a gap just above the cutoff.
Under RD, we assume that there is no manipulation in the running variable. However, bunching behavior, where firms or individuals strategically manipulate their position, violates this assumption.
To address this issue, the bunching approach estimates the counterfactual distribution, what the density of individuals would have been in the absence of manipulation.
The fraction of individuals who engaged in manipulation is then calculated by comparing the observed distribution to this counterfactual distribution.
In a standard RD framework, this step is unnecessary because it assumes that the observed distribution and the counterfactual (manipulation-free) distribution are the same, implying no manipulation
27.6.2.1 McCrary Sorting Test
A widely used formal test is the McCrary density test (McCrary 2008), later refined by Cattaneo, Idrobo, and Titiunik (2019).
- Null Hypothesis (\(H_0\)): The density of the running variable is continuous at the cutoff.
- Alternative Hypothesis (\(H_a\)): A discontinuity (jump) in the density function at the cutoff, suggesting manipulation.
- Interpretation:
- A significant discontinuity suggests manipulation, violating RD assumptions.
- A failure to reject \(H_0\) does not necessarily confirm validity, as some forms of manipulation may remain undetected.
- If there is two-sided manipulation, this test will fail to detect it.
27.6.2.2 Guidelines for Assessing Manipulation
- J. L. Zhang and Rubin (2003), Lee (2009), and Aronow, Baron, and Pinson (2019) provide criteria for evaluating manipulation risks.
- Knowing your research design inside out is crucial to anticipating possible manipulation attempts.
- Manipulation is often one-sided, meaning subjects shift only in one direction relative to the cutoff. In rare cases, two-sided manipulation may occur but often cancels out.
- We could also observe partial manipulation in reality (e.g., when subjects can only imperfectly manipulate). However, since we typically treat it like a fuzzy RD, we would not encounter identification problems. In contrast, complete manipulation would lead to serious identification issues.
Bunching Methodology
- Bunching occurs when individuals self-select into specific values of the running variable (e.g., policy thresholds). See Kleven (2016) for a review.
- The method helps estimate the counterfactual distribution (what the density would have been without manipulation).
- The fraction of individuals who manipulated can be estimated by comparing observed densities to the counterfactual.
If the running variable and outcome are simultaneously determined, a modified RD estimator can be used for consistent estimation (Bajari et al. 2011):
- One-sided manipulation: Individuals shift only in one direction relative to the cutoff (similar to the monotonicity assumption in instrumental variables).
- Bounded manipulation (regularity assumption): The density of individuals far from the threshold remains unaffected (Blomquist et al. 2021; Bertanha, McCallum, and Seegert 2021).
27.6.2.3 Steps for Bunching Analysis
- Identify the window where bunching occurs (based on Bosch, Dekker, and Strohmaier (2020)). Perform robustness checks by varying the manipulation window.
- Estimate the manipulation-free counterfactual distribution.
- Standard errors for inference can be calculated (following Chetty, Hendren, and Katz (2016)), where bootstrap resampling of residuals is used in estimating the counts of individuals within bins. However, this step may be unnecessary for large datasets.
If the bunching test fails to detect manipulation, we proceed to the Placebo Test.
McCrary Density Test (Discontinuity in Forcing Variable)
Figure 27.1 shows simulated data without discontinuity.
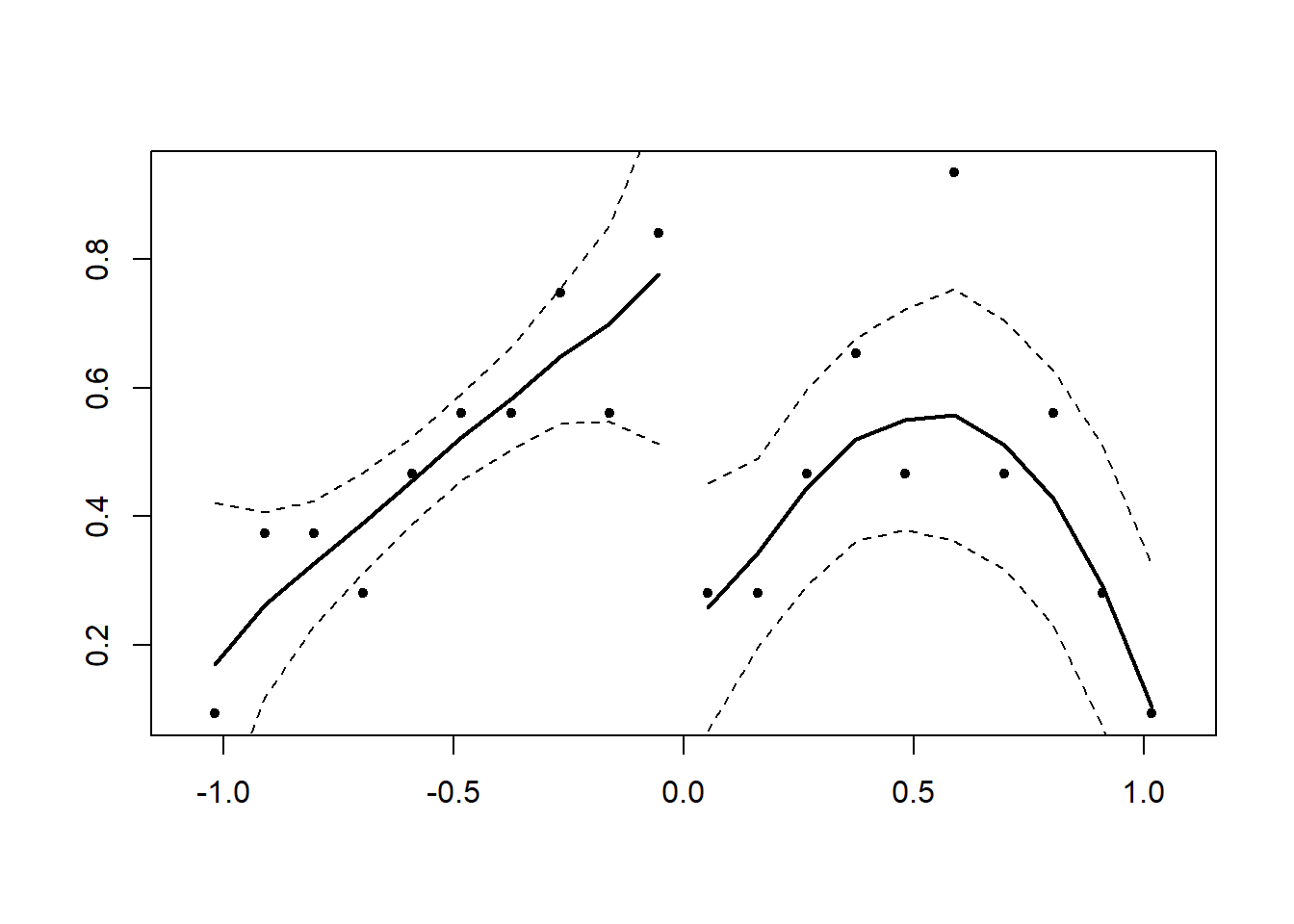
Figure 27.1: Local Polynomial Regression without Discontinuity at Cutoff
#> [1] 0.06355195Figure 27.2 shows simulated data with discontinuity.
# Simulated data with discontinuity
x <- runif(1000, -1, 1)
x <- x + 2 * (runif(1000, -1, 1) > 0 & x < 0)
DCdensity(x, 0) # Discontinuity detected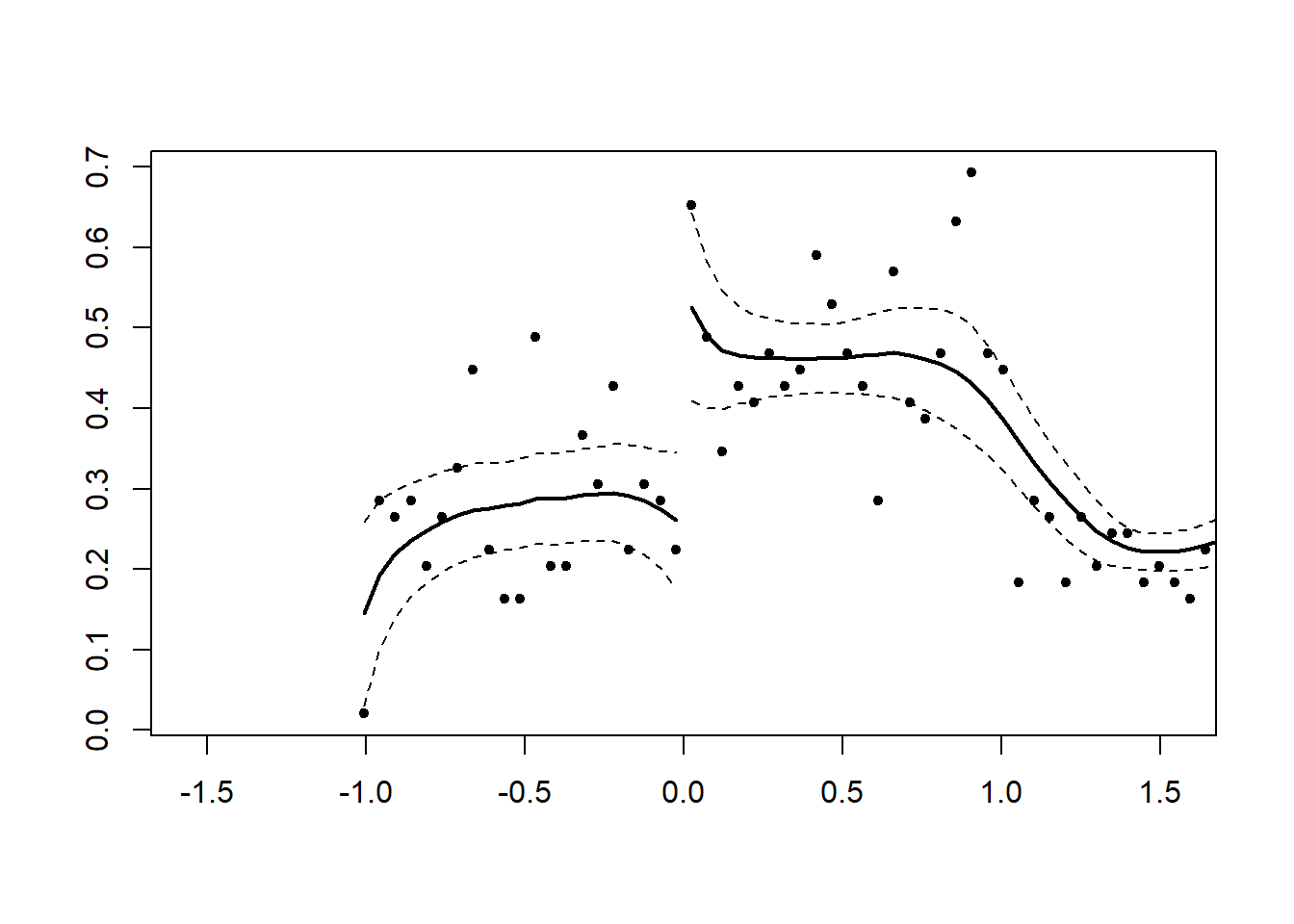
Figure 27.2: Local Polynomial Regression with Discontinuity at Cutoff
#> [1] 0.001936782Cattaneo Density Test (Improved Version)
library(rddensity)
# Simulated continuous density
set.seed(1)
x <- rnorm(100, mean = -0.5)
rdd <- rddensity(X = x, vce = "jackknife")
summary(rdd)
#>
#> Manipulation testing using local polynomial density estimation.
#>
#> Number of obs = 100
#> Model = unrestricted
#> Kernel = triangular
#> BW method = estimated
#> VCE method = jackknife
#>
#> c = 0 Left of c Right of c
#> Number of obs 66 34
#> Eff. Number of obs 38 25
#> Order est. (p) 2 2
#> Order bias (q) 3 3
#> BW est. (h) 0.922 0.713
#>
#> Method T P > |T|
#> Robust 0.6715 0.5019
#>
#>
#> P-values of binomial tests (H0: p=0.5).
#>
#> Window Length <c >=c P>|T|
#> 0.563 + 0.563 26 20 0.4614
#> 0.603 + 0.580 27 20 0.3817
#> 0.643 + 0.596 30 20 0.2026
#> 0.683 + 0.613 32 21 0.1690
#> 0.722 + 0.630 32 22 0.2203
#> 0.762 + 0.646 33 22 0.1770
#> 0.802 + 0.663 33 23 0.2288
#> 0.842 + 0.680 35 24 0.1925
#> 0.882 + 0.696 36 24 0.1550
#> 0.922 + 0.713 38 25 0.1299
# Plot requires customization (refer to package documentation)
# rdplotdensity(rdd, x,
# xlabel = "Running Variable",
# ylabel = "Density")27.6.3 Placebo Tests
Placebo tests, also known as falsification checks, assess whether discontinuities appear at points other than the treatment cutoff. This helps verify that observed effects are causal rather than artifacts of the method or data.
- There should be no jumps in the outcome at values other than the cutoff (\(X_i < c\) or \(X_i \geq c\)).
- The test involves shifting the cutoff along the running variable while using the same bandwidth to check for discontinuities in the conditional mean of the outcome.
- This approach is similar to balance checks in experimental design, ensuring no pre-existing differences. Remember, we can only test on observables, not unobservables.
Under a valid RD design, matching methods are unnecessary. Just as with randomized experiments, balance should naturally occur across the threshold. If adjustments are required, it suggests the RD assumptions may be invalid.
27.6.3.1 Applications of Placebo Tests
- Testing No Discontinuity in Predetermined Covariates: Covariates that should not be affected by treatment should not exhibit a jump at the cutoff.
- Testing Other Discontinuities: Checking for discontinuities at other arbitrary points along the running variable.
- Using Placebo Outcomes: If an outcome variable that should not be affected by treatment shows a significant discontinuity, this raises concerns about RD validity.
- Assessing Sensitivity to Covariates: RD estimates should not be highly sensitive to the inclusion or exclusion of covariates.
27.6.3.2 Mathematical Specification
The balance of observable characteristics on both sides of the threshold can be tested using:
\[ Z_i = \alpha_0 + \alpha_1 f(X_i) + I(X_i \geq c) \alpha_2 + [f(X_i) \times I(X_i \geq c)]\alpha_3 + u_i \]
where:
\(X_i\) = running variable
\(Z_i\) = predetermined characteristics (e.g., age, education, etc.)
\(\alpha_2\) should be zero if \(Z_i\) is unaffected by treatment.
If multiple covariates \(Z_i\) are tested simultaneously, simulating their joint distribution avoids false positives due to multiple comparisons. This step is unnecessary if covariates are independent, but such independence is unlikely in practice.
27.6.4 Sensitivity to Bandwidth Choice
The choice of bandwidth is crucial in RD estimation. Different bandwidth selection methods exist:
- Ad-hoc or Substantively Driven: Based on theoretical or empirical reasoning.
- Data-Driven Selection (Cross-Validation): Optimizes bandwidth to minimize prediction error.
- Conservative Approach: Uses robust optimal bandwidth selection methods (e.g., (Calonico, Cattaneo, and Farrell 2020)).
The objective is to minimize mean squared error (MSE) between estimated and actual treatment effects.
27.6.5 Assessing Sensitivity
- Results should be consistent across reasonable bandwidth choices.
- The optimal bandwidth for estimating treatment effects may differ from the optimal bandwidth for testing covariates but should be fairly close.
# Load required package
library(rdd)
# Simulate some data
set.seed(123)
n <- 100 # Sample size
# Running variable centered around 0
running_var <- runif(n, -1, 1)
# Treatment assigned at cutpoint 0
treatment <- ifelse(running_var >= 0, 1, 0)
# Outcome variable
outcome_var <- 2 * running_var + treatment * 1.5 + rnorm(n)
# Compute the optimal Imbens-Kalyanaraman bandwidth
bandwidth <-
IKbandwidth(running_var,
outcome_var,
cutpoint = 0,
kernel = "triangular")
# Print the bandwidth
print(bandwidth)
#> [1] 0.437414227.6.6 Manipulation-Robust Regression Discontinuity Bounds
Regression Discontinuity designs rely on the assumption that the running variable \(X_i\) is not manipulable by agents in the study. However, McCrary (2008) showed that a discontinuity in the density of \(X_i\) at the cutoff may indicate manipulation, potentially invalidating RD estimates. The common approach to handling detected manipulation is:
- If no manipulation is detected, proceed with RD analysis.
- If manipulation is detected, use the “doughnut-hole” method (i.e., excluding near-cutoff observations), but this contradicts the RD principles (Table 27.2).
However, strict adherence to this rule can lead to two problems:
- False Negatives: A small sample size might fail to detect manipulation, leading to biased estimates if manipulation still affects the running variable.
- Loss of Informative Data: Even when manipulation is detected, the data may still contain valuable information for causal inference.
To address these challenges, Gerard, Rokkanen, and Rothe (2020) introduce a framework that accounts for manipulated observations rather than discarding them. This approach:
- Identifies the extent of manipulation.
- Computes worst-case bounds on treatment effects.
- Provides a systematic way to incorporate manipulated observations while maintaining the credibility of RD analysis.
If manipulation is believed to be unlikely, an alternative approach is to conduct sensitivity analysis by:
Testing how different hypothetical values of \(\tau\) affect the bounds.
Comparing results across various \(\tau\) assumptions to assess robustness.
Consider independent observations \((X_i, Y_i, D_i)\):
- \(X_i\): Running variable.
- \(Y_i\): Outcome variable.
- \(D_i\): Treatment indicator (\(D_i = 1\) if \(X_i \geq c\), and \(D_i = 0\) otherwise).
A sharp RD design satisfies \(D_i = I(X_i \geq c)\), while a fuzzy RD design allows probabilistic treatment assignment.
The population consists of two types of units:
- Potentially-Assigned Units (\(M_i = 0\)): These units follow the standard RD framework. They have potential outcomes \(Y_i(d)\) and potential treatment states \(D_i(x)\).
- Always-Assigned Units (\(M_i = 1\)): These units always appear on one side of the cutoff and do not require potential outcomes.
If no always-assigned units exist (\(M_i = 1\) for no units), the standard RD model holds.
27.6.6.1 Key Assumptions
-
Local Independence and Continuity:
- Treatment probability jumps at \(c\) among potentially-assigned units: \[ P(D = 1|X = c^+, M = 0) > P(D = 1|X = c^-, M = 0). \]
- No defiers: \(P(D^+ \geq D^- | X = c, M = 0) = 1\).
- Potential outcomes and treatment states are continuous at \(c\).
- The density of the running variable among potentially-assigned units, \(F_{X|M=0}(x)\), is differentiable at \(c\).
-
Smoothness of the Running Variable among Potentially-Assigned Units:
- The derivative of \(F_{X|M=0}(x)\) is continuous at \(c\).
-
Restrictions on Always-Assigned Units:
- Always-assigned units satisfy \(P(X \geq c|M = 1) = 1\).
- The density of the running variable among always-assigned units, \(F_{X|M=1}(x)\), is right-differentiable at \(c\).
- This one-sided manipulation assumption allows identification of the proportion of always-assigned units.
When always-assigned units exist, the RD design effectively becomes fuzzy, since: 1. Some potentially-assigned units receive treatment while others do not. 2. Always-assigned units are always treated (or always untreated).
27.6.6.2 Estimating Treatment Effects
For potentially-assigned units, the causal effect of interest is:
\[ \Gamma = E[Y(1) - Y(0) | X = c, D^+ > D^-, M = 0]. \]
This parameter represents the local average treatment effect for potentially-assigned compliers, i.e., those whose treatment status is affected by their running variable crossing the cutoff.
27.6.6.3 Bounding Treatment Effects
The approach to bounding treatment effects consists of two key steps:
-
Estimating the Proportion of Always-Assigned Units:
- This is done by measuring the discontinuity in the density of \(X\) at \(c\).
- The larger the discontinuity, the greater the fraction of always-assigned units.
-
Computing Worst-Case Bounds on Treatment Effects:
- If manipulation exists, treatment effects must be inferred using extreme-case scenarios.
- For sharp RD designs, bounds are estimated by trimming extreme outcomes near the cutoff.
- For fuzzy RD designs, additional adjustments are required to account for the presence of always-assigned units.
Extensions of this approach use covariates and economic behavior assumptions to refine bounds further.
| Manipulation-Robust RD | Doughnut-Hole RD |
|---|---|
| Uses actual observed data at the cutoff. | Excludes observations near the cutoff. |
| Provides a direct estimate of causal effects. | Relies on extrapolation from other regions. |
| Accounts for manipulation explicitly. | Assumes a hypothetical counterfactual world. |
| Less sensitive to assumptions about manipulation. | Requires strong assumptions about bias. |
27.6.6.4 Identification Challenges
A central challenge in manipulation-robust RD designs is the inability to directly distinguish always-assigned from potentially-assigned units. As a result, the LATE \(\Gamma\) is not point identified. Instead, we establish sharp bounds on \(\Gamma\).
These bounds leverage the stochastic dominance of potential outcome cumulative distribution functions over observed distributions. This allows us to infer treatment effects without making strong parametric assumptions.
To formalize the population structure, we define five types of units:
-
Potentially-Assigned Units:
- \(C_0\) (Compliers): Receive treatment if and only if \(X \geq c\).
- \(A_0\) (Always-Takers): Always receive treatment, regardless of \(X\).
- \(N_0\) (Never-Takers): Never receive treatment, regardless of \(X\).
-
Always-Assigned Units:
- \(T_1\) (Treated Always-Assigned Units): Always appear above the cutoff and receive treatment.
- \(U_1\) (Untreated Always-Assigned Units): Always appear below the cutoff and do not receive treatment.
The measure \(\tau\), representing the proportion of always-assigned units near the cutoff, is point-identified using the discontinuity in the density of the running variable \(f_X\) at \(c\).
27.6.6.4.1 Identification in Sharp RD
In a sharp RD design:
- Units to the left of the cutoff are potentially-assigned units.
- The observed distribution of untreated outcomes, \(Y(0)\), among these units corresponds to the outcomes of potentially-assigned compliers (\(C_0\)) at the cutoff.
- To estimate sharp bounds on \(\Gamma\), we need to assess the distribution of treated outcomes (\(Y(1)\)) for compliers.
However, information on treated outcomes (\(Y(1)\)) at the cutoff is only available from the treated subpopulation, which includes:
Potentially-assigned compliers (\(C_0\))
Always-assigned treated units (\(T_1\))
Since \(\tau\) is point-identified, we can construct sharp bounds on \(\Gamma\) by adjusting for the presence of \(T_1\).
27.6.6.4.2 Identification in Fuzzy RD
In fuzzy RD, treatment assignment is not deterministic.
- Unit Types and Combinations: There are five distinct unit types and four combinations of treatment assignments and decisions relevant to the analysis. These distinctions are important because they affect how potential outcomes are analyzed and bounded.
- Outcome Distributions: The analysis involves estimating the distribution of potential outcomes (both treated and untreated) among potentially-assigned compliers at the cutoff.
- The goal is to estimate the distribution of potential outcomes (both treated and untreated) for potentially-assigned compliers at the cutoff.
27.6.6.5 Three-Step Process for Bounding Treatment Effects
The method to obtain sharp bounds on \(\Gamma\) follows three steps:
- Bounding Potential Outcomes Under Treatment:
- Use observed treated outcomes to estimate the upper and lower bounds on \(F_{Y(1)}(y | X = c, M = 0)\).
- Bounding Potential Outcomes Under Non-Treatment:
- Use observed untreated outcomes to estimate the upper and lower bounds on \(F_{Y(0)}(y | X = c, M = 0)\).
- Deriving Bounds on \(\Gamma\):
- Using the bounds from Steps 1 and 2, compute sharp upper and lower bounds on the local average treatment effect.
Extreme Value Consideration:
- The bounds account for worst-case scenarios by considering extreme assumptions about the distribution of potential outcomes.
- These bounds are sharp (i.e., they cannot be tightened further without additional assumptions) but remain empirically relevant.
27.6.6.6 Extensions
- Quantile Treatment Effects (QTEs)
An alternative to average treatment effects is the quantile treatment effect (QTE), which focuses on different percentiles of the outcome distribution. Advantages of QTE bounds include:
- Less Sensitivity to Extreme Values: Unlike ATE bounds, QTE bounds are less affected by outliers in the outcome distribution.
- More Informative for Policy Analysis: Helps determine whether effects are concentrated in certain segments of the population.
QTE vs. ATE Under Manipulation:
- ATE inference is highly sensitive to manipulation, with confidence intervals widening significantly as assumed manipulation increases.
- QTE inference remains meaningful even under substantial manipulation.
- Discrete Outcome Extensions: The framework applies not only to continuous outcomes but also to discrete outcome variables.
- Role of Behavioral Assumptions
- Making behavioral assumptions about high treatment likelihood among always-assigned units can refine the bounds.
- For example, assuming that most always-assigned units are treated allows for narrower bounds on treatment effects.
- Incorporation of Covariates
- Including pre-treatment covariates can refine treatment effect bounds.
- Covariates help:
- Distinguish between potentially-assigned and always-assigned units.
- Improve inference on treatment effect heterogeneity.
- Guide policy targeting by identifying unit types based on observed characteristics.
devtools::install_github("francoisgerard/rdbounds/R")
library(formattable)
library(data.table)
library(rdbounds)
set.seed(123)
df <- rdbounds_sampledata(1000, covs = FALSE)
#> [1] "True tau: 0.117999815082062"
#> [1] "True treatment effect on potentially-assigned: 2"
#> [1] "True treatment effect on right side of cutoff: 2.35399944524618"
head(df)
#> x y treatment
#> 1 -1.2532616 2.684827 0
#> 2 -0.5146925 5.845219 0
#> 3 3.4853777 6.166070 0
#> 4 0.1576616 3.227139 0
#> 5 0.2890962 7.031685 1
#> 6 3.8350019 10.238570 1
rdbounds_est <-
rdbounds(
y = df$y,
x = df$x,
# covs = as.factor(df$cov),
treatment = df$treatment,
c = 0,
discrete_x = FALSE,
discrete_y = FALSE,
bwsx = c(.2, .5),
bwy = 1,
# for median effect use
# type = "qte",
# percentiles = .5,
kernel = "epanechnikov",
orders = 1,
evaluation_ys = seq(from = 0, to = 15, by = 1),
refinement_A = TRUE,
refinement_B = TRUE,
right_effects = TRUE,
yextremes = c(0, 15),
num_bootstraps = 5
)
#> [1] "The proportion of always-assigned units just to the right of the cutoff is estimated to be 0.38047"
#> [1] "2025-11-04 09:27:50.247255 Estimating CDFs for point estimates"
#> [1] "2025-11-04 09:27:50.444951 .....Estimating CDFs for units just to the right of the cutoff"
#> [1] "2025-11-04 09:27:52.273855 Estimating CDFs with nudged tau (tau_star)"
#> [1] "2025-11-04 09:27:52.314649 .....Estimating CDFs for units just to the right of the cutoff"
#> [1] "2025-11-04 09:27:55.210347 Beginning parallelized output by bootstrap.."
#> [1] "2025-11-04 09:27:59.760454 Computing Confidence Intervals"
#> [1] "2025-11-04 09:28:11.395259 Time taken:0.35 minutes"
rdbounds_summary(rdbounds_est, title_prefix = "Sample Data Results")
#> [1] "Time taken: 0.35 minutes"
#> [1] "Sample size: 1000"
#> [1] "Local Average Treatment Effect:"
#> $tau_hat
#> [1] 0.3804665
#>
#> $tau_hat_CI
#> [1] 0.4180576 1.4333618
#>
#> $takeup_increase
#> [1] 0.6106973
#>
#> $takeup_increase_CI
#> [1] 0.4332132 0.7881814
#>
#> $TE_SRD_naive
#> [1] 1.589962
#>
#> $TE_SRD_naive_CI
#> [1] 1.083977 2.095948
#>
#> $TE_SRD_bounds
#> [1] 0.7165801 2.3454868
#>
#> $TE_SRD_CI
#> [1] -1.200992 7.733214
#>
#> $TE_SRD_covs_bounds
#> [1] NA NA
#>
#> $TE_SRD_covs_CI
#> [1] NA NA
#>
#> $TE_FRD_naive
#> [1] 2.583271
#>
#> $TE_FRD_naive_CI
#> [1] 1.506573 3.659969
#>
#> $TE_FRD_bounds
#> [1] 1.273896 3.684860
#>
#> $TE_FRD_CI
#> [1] -1.266341 10.306116
#>
#> $TE_FRD_bounds_refinementA
#> [1] 1.273896 3.684860
#>
#> $TE_FRD_refinementA_CI
#> [1] -1.266341 10.306116
#>
#> $TE_FRD_bounds_refinementB
#> [1] 1.420594 3.677963
#>
#> $TE_FRD_refinementB_CI
#> [1] NA NA
#>
#> $TE_FRD_covs_bounds
#> [1] NA NA
#>
#> $TE_FRD_covs_CI
#> [1] NA NA
#>
#> $TE_SRD_CIs_manipulation
#> [1] NA NA
#>
#> $TE_FRD_CIs_manipulation
#> [1] NA NA
#>
#> $TE_SRD_right_bounds
#> [1] -2.056178 3.650820
#>
#> $TE_SRD_right_CI
#> [1] -11.044937 9.282217
#>
#> $TE_FRD_right_bounds
#> [1] -2.900703 5.272370
#>
#> $TE_FRD_right_CI
#> [1] -14.75421 15.58640
rdbounds_est_tau <-
rdbounds(
y = df$y,
x = df$x,
# covs = as.factor(df$cov),
treatment = df$treatment,
c = 0,
discrete_x = FALSE,
discrete_y = FALSE,
bwsx = c(.2, .5),
bwy = 1,
kernel = "epanechnikov",
orders = 1,
evaluation_ys = seq(from = 0, to = 15, by = 1),
refinement_A = TRUE,
refinement_B = TRUE,
right_effects = TRUE,
potential_taus = c(.025, .05, .1, .2),
yextremes = c(0, 15),
num_bootstraps = 5
)
#> [1] "The proportion of always-assigned units just to the right of the cutoff is estimated to be 0.38047"
#> [1] "2025-11-04 09:28:12.885175 Estimating CDFs for point estimates"
#> [1] "2025-11-04 09:28:13.09748 .....Estimating CDFs for units just to the right of the cutoff"
#> [1] "2025-11-04 09:28:14.953451 Estimating CDFs with nudged tau (tau_star)"
#> [1] "2025-11-04 09:28:14.993297 .....Estimating CDFs for units just to the right of the cutoff"
#> [1] "2025-11-04 09:28:17.846789 Beginning parallelized output by bootstrap.."
#> [1] "2025-11-04 09:28:22.689488 Estimating CDFs with fixed tau value of: 0.025"
#> [1] "2025-11-04 09:28:22.761353 Estimating CDFs with fixed tau value of: 0.05"
#> [1] "2025-11-04 09:28:22.801681 Estimating CDFs with fixed tau value of: 0.1"
#> [1] "2025-11-04 09:28:22.842152 Estimating CDFs with fixed tau value of: 0.2"
#> [1] "2025-11-04 09:28:23.877805 Beginning parallelized output by bootstrap x fixed tau.."
#> [1] "2025-11-04 09:28:26.637232 Computing Confidence Intervals"
#> [1] "2025-11-04 09:28:37.92136 Time taken:0.42 minutes"Figure 27.3 shows the average treatment effect across different shares of always-assigned units.
causalverse::plot_rd_aa_share(rdbounds_est_tau) # For SRD (default)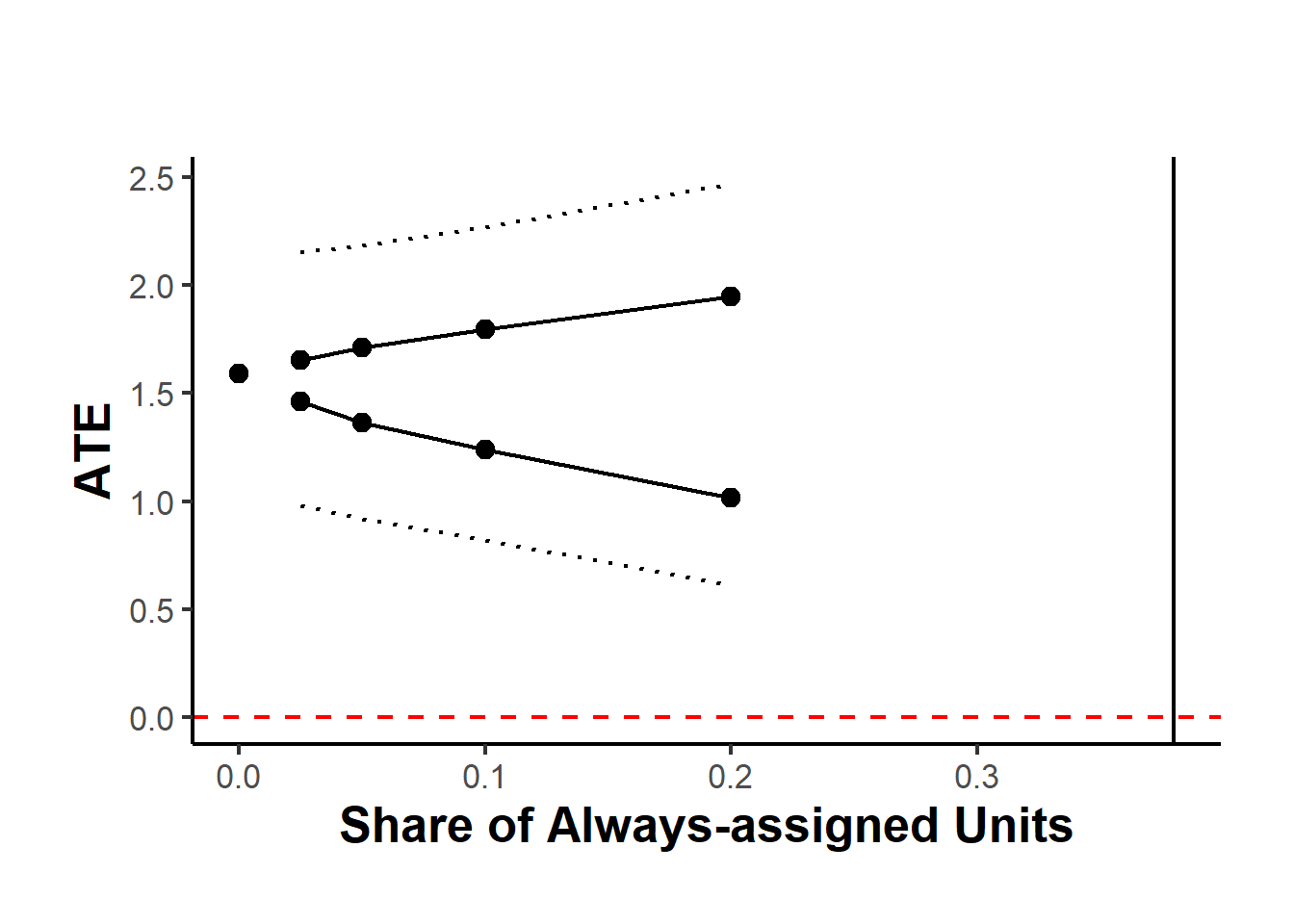
Figure 27.3: Robustness of Average Treatment Effect to Share of Always-assigned Units
# causalverse::plot_rd_aa_share(rdbounds_est_tau, rd_type = "FRD") # For FRD27.7 Fuzzy Regression Discontinuity Design
A Fuzzy Regression Discontinuity Design occurs when the assignment rule at the cutoff does not perfectly determine treatment status but instead causes a discontinuity in the probability of treatment. Unlike a Sharp RD Design, where crossing the threshold fully determines treatment, in a fuzzy RD, some individuals on both sides of the threshold may or may not receive the treatment.
If treatment is not strictly assigned at the cutoff, the usual RD estimator (which assumes deterministic assignment) is not valid. Instead, we use the cutoff as an instrumental variable to estimate the treatment effect for compliers (i.e., individuals whose treatment status depends on whether they cross the threshold).
Define an indicator variable \(Z_i\) (i.e., instrument for treatment assignment) that captures whether an individual is above or below the cutoff:
\[ Z_i = \begin{cases} 1 & \text{if } X_i \geq c \\ 0 & \text{if } X_i < c \end{cases} \]
This variable \(Z_i\) serves as an instrument for the treatment variable \(D_i\) because:
It strongly correlates with treatment (\(D_i\)).
It is exogenous, meaning it affects the outcome only through its effect on treatment.
27.7.1 Compliance Types
Since treatment assignment is no longer deterministic, individuals can be classified into four groups based on how they respond to the cutoff:
- Compliers (\(C_0\)): Individuals who receive treatment if and only if \(X_i \geq c\).
- Always-Takers (\(A_0\)): Individuals who always receive treatment, regardless of whether \(X_i \geq c\).
- Never-Takers (\(N_0\)): Individuals who never receive treatment, even if \(X_i \geq c\).
- Defiers (violating monotonicity, assumed to be zero): Individuals who receive treatment if \(X_i < c\) but not if \(X_i \geq c\).
The Fuzzy RD estimator identifies the treatment effect only for compliers, because their treatment status depends on \(Z_i\).
27.7.2 Estimating the Local Average Treatment Effect
We estimate the LATE using a ratio of discontinuities:
\[ \text{LATE} = \frac{\lim\limits_{x \downarrow c}E[Y|X = x] - \lim\limits_{x \uparrow c}E[Y|X = x]}{\lim\limits_{x \downarrow c } E[D |X = x] - \lim\limits_{x \uparrow c}E[D |X=x]} \]
Intuitively, this formula represents:
\[ \text{LATE} = \frac{\text{Discontinuity in } E[Y|X]}{\text{Discontinuity in } E[D|X]} \]
where:
The numerator captures the jump in the expected outcome at the cutoff.
The denominator captures the jump in the probability of treatment at the cutoff.
This ratio is valid under three key assumptions:
- Continuity in potential outcomes: \(E[Y(d)|X]\) is continuous at \(X = c\) for both \(d \in \{0,1\}\).
- Monotonicity: There are no defiers (\(P(D^+ \geq D^- | X = c) = 1\)).
- First-stage relevance: There is a discontinuity in \(P(D = 1 | X)\) at \(X = c\).
If these conditions hold, the fuzzy RD estimator gives a valid estimate of the causal effect of treatment for compliers.
27.7.3 Equivalent Representation Using Expectations
We can also define LATE in terms of conditional expectations of treatment and outcome:
\[ \lim_{\epsilon \to 0} \frac{E[Y |Z = 1] - E[Y |Z=0]}{E[D|Z = 1] - E[D|Z = 0]} \]
where \(Z\) is the instrument (indicator for being above the cutoff). This approach highlights the IV nature of fuzzy RD.
27.7.4 Estimation Strategies
There are two equivalent ways to estimate the LATE in practice:
Approach 1: Two-Step Estimation
-
Estimate Sharp RD for the Outcome \(Y\):
- Regress \(Y\) on \(X\) using a local linear regression on either side of \(c\).
- Estimate the discontinuity in \(E[Y|X]\) at \(c\).
-
Estimate Sharp RD for the Treatment \(D\):
- Regress \(D\) on \(X\) using a local linear regression on either side of \(c\).
- Estimate the discontinuity in \(E[D|X]\) at \(c\).
-
Compute the Ratio:
- Divide the estimated discontinuity in \(E[Y|X]\) by the estimated discontinuity in \(E[D|X]\).
Mathematically:
\[ \widehat{\text{LATE}} = \frac{\widehat{E[Y \mid X = c^+]} - \widehat{E[Y \mid X = c^-]}}{\widehat{E[D \mid X = c^+]} - \widehat{E[D \mid X = c^-]}} \] Approach 2: Instrumental Variables Regression
Subset the data to observations close to \(c\).
-
Use \(Z_i\) (above/below cutoff indicator) as an instrument for \(D_i\) in a two-stage least squares regression:
-
First-stage regression (predicting treatment using the cutoff indicator):
\[ D_i = \alpha + \beta Z_i + \gamma X_i + \epsilon_i \]
- This captures the effect of the cutoff on treatment assignment.
-
Second-stage regression (estimating treatment effect using predicted \(D_i\)):
\[ Y_i = \delta + \tau \widehat{D}_i + \lambda X_i + \nu_i \]
- The coefficient \(\tau\) gives the LATE estimate.
-
27.7.5 Practical Considerations
- Bandwidth Selection: Only observations near the cutoff should be used. Methods like cross-validation or Calonico, Cattaneo, and Farrell (2020) optimal bandwidth selection can help.
- Polynomial Order: A local linear model is typically preferred, but higher-order polynomials may be used cautiously.
- Robust Inference: Standard errors should be computed using heteroskedasticity-robust and clustered standard errors if necessary.
- Strong first-stage (e.g., \(F\)-stat \(\ge\) 16); no exclusion restriction violations; same model for both outcome and treatment take-up.
27.7.6 Steps for Fuzzy RD
1. Visualization
- Graph the Outcome Variable:
- Compute the average outcome within bins of the running variable \(X_i\).
- Choose bins large enough to display smooth trends but small enough to reveal discontinuities at the cutoff.
- Overlay a smoothed regression line on either side of the cutoff to visualize any jumps.
- Graph the Probability of Treatment:
- Compute the average treatment probability within the same bins.
- Plot \(E[D|X]\) to check for a discontinuity at \(X = c\), confirming the first-stage relevance of the instrument.
2. Estimation of Treatment Effect
Use Two-Stage Least Squares to estimate the Local Average Treatment Effect:
- First Stage (Predict Treatment Using Cutoff Indicator \(Z_i\)): \[
D_i = \alpha + \beta Z_i + \gamma X_i + \epsilon_i
\]
- This regression captures how treatment probability changes at the cutoff.
- The coefficient \(\beta\) measures the jump in treatment probability at \(X = c\).
- Second Stage (Estimate Outcome Using Predicted Treatment): \[
Y_i = \delta + \tau \widehat{D}_i + \lambda X_i + \nu_i
\]
- The coefficient \(\tau\) gives the LATE, which estimates the treatment effect for compliers.
3. Robustness Checks
- Assess Possible Jumps in Other Covariates:
- Check whether other pre-determined covariates (e.g., age, income) exhibit discontinuities at the cutoff.
- If covariates jump, this may indicate endogenous sorting or omitted variable bias.
- Hypothesis Testing for Bunching (McCrary Test):
- Test for manipulation of the running variable by examining whether the density of \(X_i\) changes discontinuously at \(c\).
- A significant density jump suggests sorting behavior, which could invalidate RD assumptions.
- Placebo Tests:
- Repeat the analysis at fake cutoffs (values of \(X\) where no intervention occurs).
- If a treatment effect appears at a placebo cutoff, this suggests a spurious RD effect.
- Varying Bandwidth Sensitivity:
- Re-run the analysis using different bandwidths around the cutoff.
- Check whether estimates remain stable as the window narrows or expands.
27.8 Sharp Regression Discontinuity Design
A Sharp Regression Discontinuity Design occurs when treatment assignment follows a strict rule at a known cutoff. That is, units receive treatment if and only if their running variable \(X_i\) crosses a threshold \(c\):
\[ D_i = \begin{cases} 1 & \text{if } X_i \geq c \\ 0 & \text{if } X_i < c \end{cases} \]
Unlike Fuzzy RD, where treatment probability changes discontinuously but is not deterministic, Sharp RD ensures perfect compliance with the cutoff rule.
The key idea is that units just below and just above the cutoff are nearly identical in expectation, except for their treatment status. This mimics randomized experiments in a local neighborhood around \(X = c\).
27.8.1 Assumptions for Identification
For a valid Sharp RD design, we assume:
-
Continuity of the Conditional Expectation of Potential Outcomes
- The expected outcome given \(X\) is smooth at \(c\) in the absence of treatment: \[ \lim_{x \uparrow c} E[Y(0) | X = x] = \lim_{x \downarrow c} E[Y(0) | X = x]. \]
- This ensures that any observed discontinuity in \(E[Y | X]\) at \(X = c\) is due to treatment, not pre-existing differences.
-
No Manipulation of the Running Variable
- Agents cannot perfectly sort themselves around the cutoff (e.g., students manipulating test scores to qualify for a scholarship).
- This is typically checked using the McCrary density test to detect discontinuities in the density of \(X\) at \(c\).
-
Local Randomization
- Near the cutoff, individuals are as good as randomly assigned to treatment or control.
If these conditions hold, the Sharp RD estimator provides an unbiased estimate of the causal effect of treatment.
27.8.2 Estimating the Local Average Treatment Effect
The treatment effect at the cutoff is given by:
\[ \tau = \lim_{x \downarrow c}E[Y | X = x] - \lim_{x \uparrow c} E[Y | X = x]. \]
This represents the jump in the expected outcome at the cutoff.
27.8.3 Estimation Methods
A common approach is to estimate separate linear regressions on each side of the cutoff:
For observations below the cutoff \((X < c)\):
\[ Y_i = \alpha + \beta (X_i - c) + \epsilon_i. \]
For observations above the cutoff \((X \geq c)\):
\[ Y_i = \gamma + \delta (X_i - c) + \tau D_i + \nu_i. \]
Here, the coefficient \(\tau\) captures the treatment effect at \(X = c\).
In practice, we estimate:
\[ \hat{\tau} = \hat{E}[Y | X = c^+] - \hat{E}[Y | X = c^-]. \]
This can be implemented using Weighted Least Squares with observations near the cutoff receiving higher weights.
- Global Polynomial Regression
An alternative approach is to use a polynomial regression:
\[ Y_i = \alpha + \sum_{k=1}^{K} \beta_k (X_i - c)^k + \tau D_i + \epsilon_i. \]
where:
Higher-order terms \((X_i - c)^k\) capture nonlinear relationships.
Typical choices for \(K\) are 2 or 3, but higher orders may lead to overfitting.
- Nonparametric Local Regression
Instead of assuming a linear or polynomial relationship, a local regression (kernel-based) method estimates:
\[ E[Y | X = x] = \sum_{i=1}^{n} K_h (X_i - x) Y_i. \]
where \(K_h\) is a kernel function (e.g., Epanechnikov), and \(h\) is the bandwidth.
- A smaller \(h\) captures local variation but increases variance.
- A larger \(h\) smooths noise but risks bias.
27.8.4 Steps for Sharp RD
- Visualization
-
Graph the outcome variable:
- Compute binned averages of \(Y_i\) over intervals of \(X\).
- Choose bin sizes that balance smoothness and clarity.
- Overlay a smoothed regression line on each side of \(c\).
-
Graph the running variable’s density:
- Use histograms to check for manipulation.
- Conduct a McCrary density test to detect discontinuities.
- Estimation of the Treatment Effect
- Run local linear regression separately on both sides of the cutoff.
- Use nonparametric methods (e.g., kernel regression) for robustness.
- Estimate treatment effect using: \[ \hat{\tau} = \hat{E}[Y | X = c^+] - \hat{E}[Y | X = c^-]. \]
- Robustness Checks
- Check for Jumps in Other Covariates
If any pre-determined covariate jumps at the cutoff, it suggests sorting or omitted variable bias.
-
Run RD regressions for each covariate:
\[ W_i = \alpha + \beta (X_i - c) + \gamma D_i + \epsilon_i. \]
A significant \(\gamma\) suggests a violation of continuity assumptions.
- McCrary Density Test (Checking for Manipulation)
- Run the McCrary test to examine whether the density of \(X_i\) exhibits a discontinuity at \(c\).
- A significant jump indicates sorting behavior, which can invalidate the RD design.
- Placebo Tests
- Perform fake cutoff tests by estimating RD effects at arbitrary points \(c^*\).
- If significant effects appear at non-cutoff points, the RD design may be picking up spurious trends.
- Varying Bandwidth
- Re-run RD analysis using different bandwidths \(h\).
- If results change dramatically, treatment effects may be highly sensitive to bandwidth choice.
- Use data-driven bandwidth selection methods (e.g., G. Imbens and Kalyanaraman (2012)).
27.9 Regression Kink Design
The Regression Kink Design (RKD) extends the logic of RD by exploiting changes in the slope of the treatment intensity function at a known threshold rather than a discontinuous jump in treatment assignment.
Instead of an RD jump in treatment probability at \(X = c\), the treatment function \(b(X)\) exhibits a kink at the cutoff:
- In Sharp RKD, the kink is deterministic, meaning the treatment function \(b(X)\) changes its slope exactly at \(X = c\).
- In Fuzzy RKD, treatment assignment remains probabilistic, requiring an instrumental variable approach similar to Fuzzy RD.
Example: Unemployment Benefits
Consider an unemployment insurance program where benefits increase at a diminishing rate as prior earnings increase. The function governing benefits, \(b(X)\), exhibits a kink at a threshold \(X = c\). The RKD framework allows us to estimate the marginal causal effect of additional benefits on employment duration.
27.9.1 Identification in Sharp Regression Kink Design
In a Sharp RKD, the treatment intensity function \(b(X)\) exhibits a known change in slope at \(X = c\), formally:
\[ D_i = b(X_i), \quad \text{where } b(X) \text{ has a kink at } X = c. \]
The key identification assumption is that the potential outcome function \(E[Y(d) | X]\) is smooth in \(X\). Thus, any observed change in the slope of \(E[Y | X]\) at \(X = c\) can be attributed to the change in \(b(X)\).
The causal effect of interest is:
\[ \alpha_{KRD} = \frac{\lim\limits_{x \downarrow c} \frac{d}{dx}E[Y |X = x]- \lim\limits_{x \uparrow c} \frac{d}{dx}E[Y |X = x]}{\lim\limits_{x \downarrow c} \frac{d}{dx}b(x) - \lim\limits_{x \uparrow c} \frac{d}{dx}b(x)}. \]
where:
\(b(X)\) is a known function determining treatment intensity.
The numerator captures the discontinuous change in the slope of the expected outcome at \(X = c\).
The denominator captures the change in the slope of the treatment function at \(X = c\).
If \(b(X)\) is known and deterministic, the denominator is non-random, allowing for precise estimation of \(\alpha_{KRD}\).
Assumptions for Identification
-
Continuity of Potential Outcomes
- The expected potential outcomes \(E[Y(d)|X]\) are smooth in \(X\) (no jumps).
-
No Manipulation of the Running Variable
- The density of \(X\) is continuous at \(X = c\), implying that agents cannot sort themselves based on the kink.
-
First-Stage Validity
- The slope of \(b(X)\) must change at \(X = c\) (i.e., the kink must exist).
If these assumptions hold, \(\alpha_{KRD}\) represents the marginal causal effect of treatment intensity on the outcome.
27.9.2 Identification in Fuzzy Regression Kink Design
In Fuzzy RKD, the treatment function \(D_i\) does not directly follow a deterministic function \(b(X)\) but instead exhibits a kink in its probability distribution:
\[ E[D | X] \text{ has a kink at } X = c. \]
The treatment intensity function is unknown, requiring an instrumental variable (IV) strategy, analogous to Fuzzy RD.
The causal effect is given by:
\[ \alpha_{KRD} = \frac{\lim\limits_{x \downarrow c} \frac{d}{dx}E[Y |X = x]- \lim\limits_{x \uparrow c} \frac{d}{dx}E[Y |X = x]}{\lim\limits_{x \downarrow c} \frac{d}{dx}E[D |X = x]- \lim\limits_{x \uparrow c} \frac{d}{dx}E[D |X = x]}. \]
where:
The numerator measures the kink in the expected outcome.
The denominator measures the kink in the probability of treatment.
The ratio provides a local instrumental variable estimate of the causal effect for compliers.
Identification Assumptions
In addition to the Sharp RKD assumptions, Fuzzy RKD requires:
-
Monotonicity
- No individuals decrease their treatment intensity while others increase at the kink (analogous to Fuzzy RD monotonicity).
-
Relevance of the Kink
- There must be a statistically significant slope change in \(E[D | X]\) at \(X = c\).
If these assumptions hold, the Fuzzy RKD estimator identifies a local treatment effect.
27.9.3 Estimation of RKD Effects
RKD estimation involves three main steps:
Step 1: Estimating the Kink in the Outcome Function
Estimate the left- and right-hand derivatives of \(E[Y | X]\):
\[ \frac{d}{dx}E[Y | X] = \lim_{h \to 0} \frac{E[Y | X = c + h] - E[Y | X = c - h]}{h}. \]
This can be done using:
Local linear regression on either side of the kink.
Higher-order polynomial regression for improved flexibility.
Step 2: Estimating the Kink in the Treatment Function
For Sharp RKD, the kink in \(b(X)\) is known.
For Fuzzy RKD, estimate the kink in \(E[D | X]\):
\[ \frac{d}{dx}E[D | X] = \lim_{h \to 0} \frac{E[D | X = c + h] - E[D | X = c - h]}{h}. \]
Use local regression or piecewise polynomials to estimate this slope.
Step 3: Compute RKD Estimator
For Sharp RKD:
\[ \hat{\alpha}_{KRD} = \frac{\hat{\tau}_Y}{\tau_b}, \]
where:
\(\hat{\tau}_Y\) is the estimated kink in \(E[Y | X]\).
\(\tau_b\) is the known slope change in \(b(X)\).
For Fuzzy RKD:
\[ \hat{\alpha}_{KRD} = \frac{\hat{\tau}_Y}{\hat{\tau}_D}. \]
where:
- \(\hat{\tau}_D\) is the estimated kink in \(E[D | X]\).
27.9.4 Robustness Checks
-
Assess Covariate Smoothness
- Verify that pre-determined covariates (e.g., age, education) do not exhibit kinks at \(X = c\).
-
Check for Manipulation of the Running Variable
- Perform a McCrary test to ensure the density of \(X\) is continuous at \(X = c\).
-
Placebo Kinks
- Test for spurious kinks at other arbitrary values of \(X\).
-
Bandwidth Sensitivity
- Estimate RKD effects with varying bandwidths to check for consistency.
27.10 Multi-Cutoff Regression Discontinuity Design
The Multi-Cutoff Regression Discontinuity Design extends the standard RD framework by allowing for multiple cutoff points across different groups or geographic regions. Instead of a single threshold \(c\), different subgroups are assigned different cutoffs \(C_i\). This framework allows for a heterogeneous treatment effect function:
\[ \tau (x,c)= E[Y_{1i} - Y_{0i}|X_i = x, C_i = c]. \]
Why Use Multi-Cutoff RD?
- Policy Variation: Policies often implement different cutoffs across regions or institutions (e.g., different states setting different minimum test scores for scholarship eligibility).
- Generalizability: Allows estimation of treatment effects across multiple populations instead of relying on a single threshold.
- Improved Precision: Leveraging multiple thresholds can enhance statistical power compared to a single-cutoff RD.
The multi-cutoff RD framework provides several advantages:
-
Estimation of Local Heterogeneous Effects
- Unlike standard RD, which estimates a single treatment effect, multi-cutoff RD allows heterogeneity in effects across groups.
-
Improved Precision
- More observations across different thresholds can increase statistical power.
-
Policy Implications
- Useful in settings where policy thresholds vary (e.g., different states setting different income eligibility limits for welfare programs).
27.10.1 Identification
Under the potential outcomes framework, each unit \(i\) has:
A running variable \(X_i\).
A cutoff specific to their group \(C_i\).
A binary treatment indicator:
\[ D_i = I(X_i \geq C_i). \]
The observed outcome is:
\[ Y_i = D_i Y_{1i} + (1 - D_i) Y_{0i}. \]
The treatment effect is the expected difference in potential outcomes:
\[ \tau(x, c) = E[Y_{1i} - Y_{0i} | X_i = x, C_i = c]. \]
27.10.2 Key Assumptions
To ensure causal identification, we extend the standard RD assumptions:
-
Continuity of Potential Outcomes
- The expected potential outcomes \(E[Y(0)|X]\) and \(E[Y(1)|X]\) are smooth functions of \(X\) at each cutoff \(C_i\).
- Formally: \[ \lim_{x \uparrow C_i} E[Y(0)|X=x, C_i=c] = \lim_{x \downarrow C_i} E[Y(0)|X=x, C_i=c]. \]
-
No Manipulation of the Running Variable
- The density of \(X_i\) must be continuous at each \(C_i\), ensuring that individuals cannot selectively sort above or below their assigned cutoff.
-
Local Randomization
- Near each cutoff, units are as-good-as-randomly assigned to treatment or control.
-
Independence Across Cutoffs
- The cutoff assignment rule should be exogenous and not correlated with unobserved determinants of \(Y\).
If these assumptions hold, each cutoff provides a valid local treatment effect estimate.
27.10.3 Estimation Approaches
27.10.3.1 Pooling Cutoffs with Fixed Effects
A straightforward way to estimate multi-cutoff RD is to include cutoff fixed effects:
\[ Y_i = \alpha + \beta (X_i - C_i) + \tau D_i + \gamma C_i + \epsilon_i. \]
where:
\(\tau\) captures the average treatment effect across all cutoffs.
\(C_i\) is included as a fixed effect to account for different intercepts across groups.
27.10.3.2 Separate RD Estimation for Each Cutoff
Instead of pooling, we can estimate separate RD effects for each \(C_i\):
\[ \tau_c = \lim_{x \downarrow C_i}E[Y|X = x, C_i = c] - \lim_{x \uparrow C_i} E[Y|X = x, C_i = c]. \]
This approach allows for heterogeneous treatment effects.
27.10.3.3 Interaction Model for Heterogeneous Effects
To estimate how treatment effects vary with \(C_i\), we interact \(D_i\) with \(C_i\):
\[ Y_i = \alpha + \beta (X_i - C_i) + \tau D_i + \lambda D_i C_i + \epsilon_i. \]
where:
\(\lambda\) captures how the treatment effect varies with the cutoff.
A significant \(\lambda\) implies that \(\tau(x, c)\) is not constant across cutoffs.
27.10.3.4 Nonparametric Local Estimation
A fully flexible approach estimates \(\tau(x, c)\) separately at each cutoff using kernel-based methods:
\[ \hat{\tau}(c) = \frac{\sum_{i=1}^{n} K_h (X_i - C_i) D_i Y_i}{\sum_{i=1}^{n} K_h (X_i - C_i) D_i} - \frac{\sum_{i=1}^{n} K_h (X_i - C_i) (1 - D_i) Y_i}{\sum_{i=1}^{n} K_h (X_i - C_i) (1 - D_i)}. \]
where:
\(K_h(\cdot)\) is a kernel function (e.g., Epanechnikov).
\(h\) is the bandwidth, chosen via cross-validation.
27.10.4 Robustness Checks
- Covariate Balance at Each Cutoff
Test whether pre-treatment covariates show jumps at each \(C_i\).
-
Run placebo RD regressions on covariates:
\[ W_i = \alpha + \beta (X_i - C_i) + \gamma D_i + \epsilon_i. \]
A significant \(\gamma\) suggests that RD assumptions are violated.
- McCrary Density Test
-
Perform a McCrary test separately at each cutoff to check for manipulation:
\[ f(X) \text{ should be continuous at } X = C_i. \]
If discontinuities exist, individuals may be sorting around cutoffs.
- Placebo Cutoffs
- Implement fake cutoffs and re-estimate \(\tau(x, c)\).
- If significant effects appear, the RD estimates may be biased.
- Varying Bandwidths
- Re-estimate treatment effects using different bandwidths.
- If \(\hat{\tau}(x,c)\) changes drastically, it suggests sensitivity to bandwidth choice.
27.11 Multi-Score Regression Discontinuity Design
The Multi-Score Regression Discontinuity Design extends the standard single-score RD and the multi-cutoff RD by introducing multiple running variables that simultaneously determine treatment eligibility. Instead of relying on a single threshold for assignment, treatment now depends on a combination of multiple continuous scores crossing predetermined cutoffs.
Multi-score RD is relevant when policy eligibility is based on multiple criteria, such as:
Education: Honors program admission based on both math and English scores.
Healthcare: Medical trial eligibility based on both BMI and blood pressure levels.
Taxation: Tax incentives based on income level and household size.
27.11.1 General Framework
Each individual \(i\) has:
Two running variables, \(X_{1i}\) and \(X_{2i}\).
Two predetermined cutoffs, \(C_1\) and \(C_2\).
A binary treatment indicator \(D_i\), assigned based on whether the individual’s scores exceed both thresholds.
The treatment effect is defined as:
\[ \tau (x_1, x_2) = E[Y_{1i} - Y_{0i} | X_{1i} = x_1, X_{2i} = x_2]. \]
This represents the local average treatment effect in a two-dimensional RD setting.
27.11.2 Identification
Under the potential outcomes framework, for each individual \(i\), we define:
\(Y_{1i}\): Potential outcome under treatment.
\(Y_{0i}\): Potential outcome under control.
\(D_i\): Treatment assignment rule.
The observed outcome is:
\[ Y_i = D_i Y_{1i} + (1 - D_i) Y_{0i}. \]
The treatment assignment mechanism follows:
\[ D_i = \begin{cases} 1 & \text{if } X_{1i} \geq C_1 \text{ and } X_{2i} \geq C_2, \\ 0 & \text{otherwise}. \end{cases} \]
27.11.3 Key Assumptions
To ensure valid causal inference, the multi-score RD framework extends the standard RD assumptions:
-
Continuity of Potential Outcomes in Both Running Variables
- The expected potential outcomes \(E[Y(0) | X_1, X_2]\) and \(E[Y(1) | X_1, X_2]\) are smooth in both \(X_1\) and \(X_2\).
- Formally: \[ \begin{aligned} \lim_{(x_1, x_2) \to (C_1, C_2)^-} E[Y(0) | X_1 = x_1, X_2 = x_2] = \\ \lim_{(x_1, x_2) \to (C_1, C_2)^+} E[Y(0) | X_1 = x_1, X_2 = x_2]. \end{aligned} \]
- Ensures that any observed discontinuity in \(E[Y | X_1, X_2]\) is attributable to treatment.
-
No Manipulation of Running Variables
- The density of \((X_1, X_2)\) must be continuous at \((C_1, C_2)\).
- No agents should be able to precisely manipulate both scores to cross the threshold.
-
Local Randomization
- Near \((C_1, C_2)\), units are as good as randomly assigned to treatment or control.
-
No Interaction Effects in Running Variables (optional)
- In some models, we assume that the effect of crossing \(C_1\) does not depend on \(C_2\) and vice versa.
If these assumptions hold, the treatment effect is identified as the discontinuity in \(E[Y | X_1, X_2]\) at \((C_1, C_2)\).
27.11.4 Estimation Approaches
27.11.4.1 Local Linear Regression in Two Dimensions
The simplest approach is to estimate separate regressions on each side of the cutoff in both dimensions:
For observations below the threshold \((C_1, C_2)\):
\[ Y_i = \alpha + \beta_1 (X_{1i} - C_1) + \beta_2 (X_{2i} - C_2) + \epsilon_i. \]
For observations above the threshold \((C_1, C_2)\):
\[ Y_i = \gamma + \delta_1 (X_{1i} - C_1) + \delta_2 (X_{2i} - C_2) + \tau D_i + \nu_i. \]
The treatment effect \(\tau\) is estimated as:
\[ \hat{\tau} = \hat{E}[Y | X_1 = C_1^+, X_2 = C_2^+] - \hat{E}[Y | X_1 = C_1^-, X_2 = C_2^-]. \]
This approach assumes local linearity, but higher-order polynomials can be used:
\[ Y_i = \alpha + \sum_{k=1}^{K} \beta_k (X_{1i} - C_1)^k + \sum_{k=1}^{K} \gamma_k (X_{2i} - C_2)^k + \tau D_i + \epsilon_i. \]
27.11.4.2 Kernel-Weighted Estimation
A more flexible approach estimates \(\tau(x_1, x_2)\) using nonparametric local regression:
\[ \hat{\tau}(x_1, x_2) = \frac{\sum_{i=1}^{n} K_h (X_{1i} - x_1) K_h (X_{2i} - x_2) D_i Y_i}{\sum_{i=1}^{n} K_h (X_{1i} - x_1) K_h (X_{2i} - x_2) D_i} - \frac{\sum_{i=1}^{n} K_h (X_{1i} - x_1) K_h (X_{2i} - x_2) (1 - D_i) Y_i}{\sum_{i=1}^{n} K_h (X_{1i} - x_1) K_h (X_{2i} - x_2) (1 - D_i)}. \]
where:
\(K_h(\cdot)\) is a kernel function (e.g., Epanechnikov).
\(h\) is the bandwidth, selected via cross-validation.
27.11.4.3 Interaction Model for Heterogeneous Effects
To assess interaction effects between running variables, estimate:
\[ Y_i = \alpha + \beta_1 (X_{1i} - C_1) + \beta_2 (X_{2i} - C_2) + \tau D_i + \lambda D_i (X_{1i} - C_1)(X_{2i} - C_2) + \epsilon_i. \]
- \(\lambda\) captures whether the treatment effect depends on both \(X_1\) and \(X_2\).
27.11.5 Robustness Checks
-
Covariate Balance in Both Dimensions
- Test whether pre-treatment covariates jump at \((C_1, C_2)\).
-
McCrary Density Test in Two Dimensions
- Verify that density of \((X_1, X_2)\) is smooth at \((C_1, C_2)\).
-
Placebo Cutoffs
- Implement fake cutoffs and re-estimate \(\tau(x_1, x_2)\).
-
Varying Bandwidths
- Re-estimate using different bandwidths for robustness.
27.12 Evaluation of a Regression Discontinuity Design
After estimating an RD model, it is crucial to evaluate whether the assumptions hold and whether the results are robust to different specifications. The key aspects of RD evaluation include:
- Graphical and formal evidence for a discontinuity in treatment and outcome variables.
-
Validation of RD assumptions, including:
- The absence of discontinuities in pre-treatment covariates.
- No manipulation of the assignment variable.
- Robustness checks for functional form and bandwidth choice.
- External validity: assessing whether results generalize beyond the cutoff.
A well-implemented RD should demonstrate a clear treatment effect at the cutoff while ensuring that no other discontinuous changes confound the effect.
27.12.1 Graphical and Formal Evidence
27.12.1.1 Visual Inspection of the RD Effect
A fundamental step in RD analysis is to plot the outcome variable against the running variable:
- Compute binned averages of \(Y_i\) for small intervals of \(X_i\).
- Overlay a smoothed polynomial regression separately for \(X < c\) and \(X \geq c\).
- A visible jump at \(X = c\) provides initial evidence of a treatment effect.
Additionally, plotting treatment probability \(P(D = 1 | X)\) ensures that assignment follows the expected RD rule.
27.12.1.2 No Discontinuity in Pre-Treatment Covariates
To rule out omitted variable bias, we check whether other covariates (age, education, prior test scores, etc.) exhibit jumps at the cutoff.
For each covariate \(W_i\), estimate:
\[ W_i = \alpha + f(X_i) \beta + \tau D_i + \epsilon_i. \]
- If \(\tau\) is statistically significant, it suggests a violation of RD assumptions.
- Covariate jumps imply that factors other than treatment may be driving the observed outcome change.
27.12.1.3 Manipulation Test (McCrary Density Test)
A critical assumption in RD is that units cannot precisely manipulate their values of \(X_i\). If individuals can selectively sort around \(c\) (e.g., students altering test scores to qualify for a scholarship), RD estimates become invalid.
To test for manipulation, we estimate the density function of \(X\) and test for a discontinuity at \(c\):
\[ \hat{f}(X) = \lim_{x \uparrow c} f(X) - \lim_{x \downarrow c} f(X). \]
A significant difference suggests sorting behavior, which violates RD assumptions.
27.12.2 Functional Form of the Running Variable
27.12.2.1 General RD Model
The most flexible RD specification includes:
A functional form \(f(X_i)\) to account for trends.
An indicator for treatment \(D_i\). - An interaction term \(D_i f(X_i)\) allowing for different slopes on each side.
\[ Y_i = \alpha_0 + f(X_i) \alpha_1 + I(X_i \geq c) \alpha_2 + f(X_i) I(X_i \geq c) \alpha_3 + u_i. \]
where:
\(\alpha_2\) captures the treatment effect at \(X = c\).
\(\alpha_3\) tests for differences in slopes across the threshold.
27.12.2.2 Simple Case: Linear RD
If \(f(X_i)\) is a linear function, we estimate:
\[ Y_i = \beta_0 + \beta_1 X_i + I(X_i \geq c) \beta_2 + \epsilon_i. \]
Figure ?? shows how to visualize the coefficients.
RD gives you \(\beta_2\) (causal effect) of \(X\) on \(Y\) at the cutoff point
In practice, everyone does
\[ Y_i = \alpha_0 + f(x) \alpha _1 + [I(x_i \ge c)]\alpha_2 + [f(x_i)\times [I(x_i \ge c)]\alpha_3 + u_i \]
Figure ?? shows how to visualize the coefficients when one uses dynamic slope.
where we estimate different slope on different sides of the line. And if you estimate \(\alpha_3\) to be no different from 0 then we return to the simple case.
27.12.2.3 Higher-Order Polynomials
A more flexible specification allows for nonlinear relationships:
\[ Y_i = \beta_0 + \beta_1 X_i + \beta_2 X_i^2 + \beta_3 X_i^3 + \tau D_i + \epsilon_i. \]
- Higher-order polynomials reduce bias but increase variance.
- Overfitting is a risk, especially with limited data near \(c\).
27.12.2.4 Nonparametric Estimation
When polynomial models are too restrictive, we use nonparametric local linear regression:
\[ \hat{E}[Y | X] = \sum_{i=1}^{n} K_h(X_i - c) Y_i. \]
where:
\(K_h(X)\) is a kernel function (e.g., Epanechnikov).
\(h\) is the bandwidth, chosen to optimize bias-variance tradeoff.
27.12.3 Bandwidth Selection
27.12.3.1 Tradeoff Between Bias and Efficiency
Choosing an appropriate bandwidth \(h\) is crucial:
Narrow \(h\) (close to \(c\)): Lower bias, but high variance.
Wider \(h\): More efficient estimates but potential bias.
27.12.4 Addressing Potential Confounders
27.12.4.1 Multiple Running Variables
If multiple forcing variables influence treatment (e.g., both math and English scores for honors eligibility), failing to account for them may introduce confounding.
A solution is to extend RD to a multi-score framework:
\[ Y_i = \alpha_0 + f(X_{1i}, X_{2i}) \alpha_1 + I(X_{1i} \geq c_1, X_{2i} \geq c_2) \alpha_2 + \epsilon_i. \]
- Controls for both scores simultaneously.
- Allows for interactions between assignment variables.
27.12.4.2 Bundling of Institutions
In cases where policies change at institutional levels (e.g., different states implementing varying minimum wages), treatment effects may reflect institutional bundling rather than individual cutoff effects.
One solution is to include institution fixed effects:
\[ Y_i = \alpha + f(X_i) \beta + \tau D_i + \gamma C_j + \epsilon_i. \]
where \(C_j\) is a categorical variable for institution \(j\).
27.12.5 External Validity in RD
While RD provides strong internal validity, its generalizability is often limited:
-
Local Nature of RD Estimates
- RD estimates apply only at the cutoff.
- Effects may not extrapolate to other values of \(X\).
-
Heterogeneous Treatment Effects
- If \(\tau\) varies across subgroups, RD estimates may not generalize.
-
Spillover Effects
- If treatment effects extend beyond the threshold (e.g., peer effects), RD assumptions may be violated.
27.13 Applications of RD Designs
Regression Discontinuity (RD) designs have widespread applications in empirical research across economics, political science, marketing, and public policy. These applications leverage threshold-based decision rules to identify causal effects in real-world settings where randomized experiments are infeasible.
Key applications include:
Marketing: Estimating the causal effects of promotions and advertising intensity.
Education: Evaluating the impact of financial aid or merit scholarships.
Healthcare: Assessing the effect of medical interventions assigned based on eligibility thresholds.
Labor Economics: Studying unemployment benefits and wage policies.
27.13.1 Applications in Marketing
RD has been widely applied in marketing research to estimate causal effects of pricing, advertising, and product positioning.
- Position Effects in Advertising
(Narayanan and Kalyanam 2015) uses an RD approach to estimate the causal impact of advertisement placement in search engines. Since ad placement follows an auction-based system, a discontinuity occurs where the top-ranked ad receives disproportionately more clicks than lower-ranked ads.
Key insights:
Higher-ranked ads generate more click-throughs, but this does not always translate into higher conversion rates.
The RD framework helps distinguish correlation from causation by leveraging the rank cutoff.
- Identifying Causal Marketing Mix Effects
(Hartmann, Nair, and Narayanan 2011) presents a nonparametric RD estimation approach to identify causal effects of marketing mix variables, such as:
Advertising budgets
Price changes
Promotional campaigns
By comparing firms just above and below an expenditure threshold, the RD framework isolates the true causal impact of marketing spending on consumer behavior.
27.13.2 R Packages for RD Estimation
Table 27.3 shows key RD Packages in R
| Feature | rdd | rdrobust | rddtools |
|---|---|---|---|
| Estimator | Local linear regression | Local polynomial regression | Local polynomial regression |
| Bandwidth Selection | (G. Imbens and Kalyanaraman 2012) | (Calonico, Cattaneo, and Titiunik 2014; G. Imbens and Kalyanaraman 2012 ; Calonico, Cattaneo, and Farrell 2020) | (G. Imbens and Kalyanaraman 2012) |
| Kernel Functions | Epanechnikov, Gaussian | Epanechnikov | Gaussian |
| Bias Correction | No | Yes | No |
| Covariate Inclusion | Yes | Yes | Yes |
| Assumption Testing | McCrary Sorting Test | No | McCrary Sorting, Covariate Distribution Tests |
For a detailed comparison, see Thoemmes, Liao, and Jin (2017) (Table 1, p. 347).
Specialized RD Packages
-
rddensity: Tests for discontinuities in the density of the running variable (useful for manipulation/bunching detection). -
rdlocrand: Implements randomization-based inference for RD. -
rdmulti: Extends RD to multiple cutoffs and multiple scores. -
rdpower: Conducts power calculations and sample selection for RD designs.
Why Use rdrobust?
- Implements local polynomial regression, providing bias correction and robust standard errors.
- Uses state-of-the-art bandwidth selection methods.
- Produces automatic RD plots for visualization.
27.13.3 Example of Regression Discontinuity in Education
We illustrate a Sharp RD using a simulated example of college GPA and future career success.
Setup:
Students qualify for a prestigious internship if their GPA ≥ 3.5.
The outcome variable is future career success (e.g., salary).
RD estimates the causal impact of the internship program on earnings.
\[ Y_i = \beta_0 + \beta_1 X_i + \beta_2 W_i + u_i \]
\[ X_i = \begin{cases} 1, W_i \ge c \\ 0, W_i < c \end{cases} \]
We simulate 100 observations, where GPA is the forcing variable and career success depends on GPA and the treatment effect.
# Set seed for reproducibility
set.seed(42)
n = 100
# Simulate GPA scores (0-4 scale)
GPA <- runif(n, 0, 4)
# Generate future success with treatment effect at GPA >= 3.5
future_success <- 10 + 2 * GPA + 10 * (GPA >= 3.5) + rnorm(n)
# Load RD package
library(rddtools)
# Format data for RD analysis
data <- rdd_data(future_success, GPA, cutpoint = 3.5)Figure 27.4 shows the scatter plot of GPA and Future Success.
# Plot RD scatterplot
plot(data, col = "red", cex = 0.5, xlab = "GPA", ylab = "Future Success")
Figure 27.4: Binned Scatter Plot of GPA and Future Success with Threshold at 3.5
We estimate the Sharp RD treatment effect using local linear regression:
# Estimate the sharp RDD model
rdd_mod <- rdd_reg_lm(rdd_object = data, slope = "same")
# Display results
summary(rdd_mod)
#>
#> Call:
#> lm(formula = y ~ ., data = dat_step1, weights = weights)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -3.08072 -0.54182 0.05352 0.54135 2.51267
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 17.21703 0.20060 85.83 <2e-16 ***
#> D 9.79856 0.31716 30.89 <2e-16 ***
#> x 2.14839 0.09914 21.67 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.9284 on 97 degrees of freedom
#> Multiple R-squared: 0.9746, Adjusted R-squared: 0.9741
#> F-statistic: 1863 on 2 and 97 DF, p-value: < 2.2e-16Figure 27.5 plots the RD regression line with binned observations:
# Plot RD regression
plot(rdd_mod, cex = 0.5, col = "red", xlab = "GPA", ylab = "Future Success")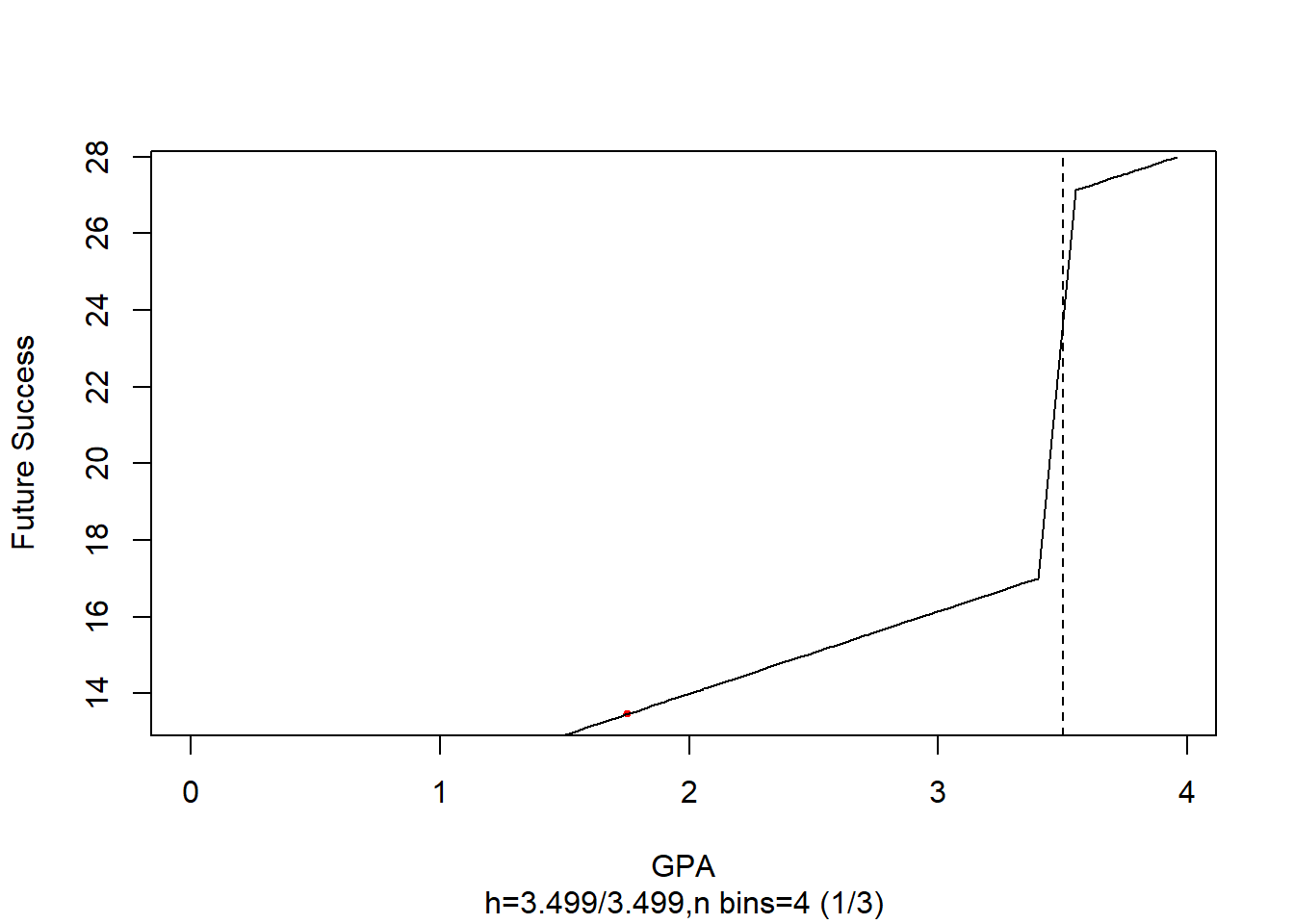
Figure 27.5: Coarse Binned Regression Discontinuity Plot of GPA and Future Success
We verify whether results hold under different bandwidths and functional forms:
- Varying the Bandwidth
# Using rdrobust for robust estimation
library(rdrobust)
# Estimate RD with optimal bandwidth
rd_out <- rdrobust(y = future_success, x = GPA, c = 3.5)
summary(rd_out)
#> Sharp RD estimates using local polynomial regression.
#>
#> Number of Obs. 100
#> BW type mserd
#> Kernel Triangular
#> VCE method NN
#>
#> Number of Obs. 83 17
#> Eff. Number of Obs. 7 12
#> Order est. (p) 1 1
#> Order bias (q) 2 2
#> BW est. (h) 0.361 0.361
#> BW bias (b) 0.670 0.670
#> rho (h/b) 0.540 0.540
#> Unique Obs. 83 17
#>
#> =====================================================================
#> Point Robust Inference
#> Estimate z P>|z| [ 95% C.I. ]
#> ---------------------------------------------------------------------
#> RD Effect 12.836 4.473 0.000 [7.677 , 19.653]
#> =====================================================================- McCrary Test for Manipulation
library(rddensity)
# Check for discontinuities in GPA distribution
rddensity(GPA, c = 3.5)
#> Call:
#> rddensity.
#> Sample size: 100. Cutoff: 3.5.
#> Model: unrestricted. Kernel: triangular. VCE: jackknife- Polynomial Functional Forms
We compare linear and quadratic specifications:
# Estimate RD with a quadratic polynomial
rdd_mod_quad <- rdd_reg_lm(rdd_object = data, slope = "separate", order = 2)
summary(rdd_mod_quad)
#>
#> Call:
#> lm(formula = y ~ ., data = dat_step1, weights = weights)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -3.06894 -0.52799 0.01642 0.55260 2.45318
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 17.30296 0.32241 53.667 < 2e-16 ***
#> D 9.14439 1.13752 8.039 2.65e-12 ***
#> x 2.29753 0.41955 5.476 3.61e-07 ***
#> `x^2` 0.04253 0.11228 0.379 0.706
#> x_right 2.51976 9.23566 0.273 0.786
#> `x^2_right` -1.61694 17.10035 -0.095 0.925
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.9376 on 94 degrees of freedom
#> Multiple R-squared: 0.9749, Adjusted R-squared: 0.9736
#> F-statistic: 731 on 5 and 94 DF, p-value: < 2.2e-1627.13.4 Example of Occupational Licensing and Market Efficiency
Occupational licensing is a form of labor market regulation that requires workers to obtain licenses or certifications before being allowed to work in specific professions. The debate around occupational licensing revolves around two competing effects:
-
Efficiency-enhancing effect:
- Licensing ensures that workers meet minimum quality standards, reducing information asymmetries between firms and consumers.
- Higher-quality service providers are selected into the labor market.
-
Barrier-to-entry effect:
- Licensing requirements impose costs on potential entrants, reducing labor supply.
- This creates frictions in the market, potentially leading to inefficiencies.
Bowblis and Smith (2021) investigates this tradeoff using a Fuzzy RD based on a threshold rule:
Nursing homes with 120 or more beds are required to hire a certain fraction of licensed/certified workers.
The study examines whether this policy improves quality of care or merely restricts labor market competition.
27.13.4.1 OLS Estimation: Naïve Approach and Its Bias
A simple Ordinary Least Squares regression can be used to estimate the effect of licensed workers on quality of service:
\[ Y_i = \alpha_0 + X_i \alpha_1 + LW_i \alpha_2 + \epsilon_i \]
where:
\(Y_i\) = Quality of service at facility \(i\).
\(LW_i\) = Proportion of licensed workers at facility \(i\).
\(X_i\) = Facility characteristics (e.g., size, staffing levels).
27.13.4.2 Potential Bias in \(\alpha_2\)
- Mitigation-Based Bias:
- Facilities with poor quality outcomes may hire more licensed workers in response to bad performance.
- This induces a negative correlation between \(LW_i\) and \(Y_i\), biasing \(\alpha_2\) downward.
- Preference-Based Bias:
- Higher-quality facilities may have greater incentives to hire certified workers.
- This induces a positive correlation between \(LW_i\) and \(Y_i\), biasing \(\alpha_2\) upward.
27.13.4.3 Fuzzy RD Framework
The OLS model is endogenous, so we implement a Fuzzy RD Design that exploits a discontinuity in licensing requirements at 120 beds.
\[ \begin{aligned}Y_{ist} = \beta_0 &+ \beta_1 \mathbb{1}(\text{Bed}_{ist} \geq 121) + \beta_2 f(\text{Size}_{ist}) \\&+ \beta_3 f(\text{Size}_{ist}) \times \mathbb{1}(\text{Bed}_{ist} \geq 121) \\&+ X_{it}'\delta + \gamma_s + \theta_t + \epsilon_{ist}\end{aligned} \]
where:
\(I(Bed \geq 121)\) = Indicator for treatment eligibility (having at least 120 beds).
\(f(Size_{ist})\) = Flexible functional form of facility size.
\(X_{it}\) = Other control variables.
\(\gamma_s\) = State fixed effects (accounts for state-level regulations).
\(\theta_t\) = Time fixed effects (accounts for temporal shocks).
\(\beta_1\) = Intent-to-treat (ITT) effect.
This model estimates discontinuities in quality outcomes at the 120-bed threshold.
27.13.4.4 Why This RD is Fuzzy
Unlike a Sharp RD, treatment is not fully determined at the cutoff:
Some facilities with fewer than 120 beds voluntarily hire licensed workers.
Some facilities with more than 120 beds may not comply fully.
Thus, the RD framework must be modified:
- Fixed-Effect Considerations:
- If states sort differently near the threshold, state fixed effects (\(\gamma_s\)) may be needed.
- However, if sorting is non-random, the RD assumption fails.
- Panel Data Implications:
- Fixed-effects models are not preferred in RD, as they are lower in the causal inference hierarchy.
- RD typically excludes pre-treatment periods, whereas fixed-effects require before-and-after comparisons.
- Variation in Facility Size:
- Hospitals rarely change bed capacity, so including hospital-specific fixed effects removes variation necessary for RD estimation.
27.13.4.5 Instrumental Variable Approach
To correct for endogeneity, we use a two-stage least squares IV approach, where the running variable serves as an instrument for treatment intensity.
Stage 1: First-Stage Regression
Estimate the probability of hiring licensed workers based on the 120-bed threshold:
\[ \begin{aligned}\text{QSW}_{ist} = \alpha_0 &+ \alpha_1 \mathbb{1}(\text{Bed}_{ist} \geq 121) + \alpha_2 f(\text{Size}_{ist}) \\&+ \alpha_3 f(\text{Size}_{ist}) \times \mathbb{1}(\text{Bed}_{ist} \geq 121) \\&+ X_{it}'\delta + \gamma_s + \theta_t + \epsilon_{ist}\end{aligned} \]
where:
- \(QSW_{ist}\) = Predicted proportion of licensed workers at facility \(i\) in state \(s\) at time \(t\).
Stage 2: Second-Stage Regression
Estimate the causal effect of hiring licensed workers on quality of service:
\[ \begin{aligned}Y_{ist} = \gamma_0 &+ \gamma_1 \widehat{\text{QSW}}_{ist} + \delta_2 f(\text{Size}_{ist}) \\&+ \delta_3 f(\text{Size}_{ist}) \times \mathbb{1}(\text{Bed}_{ist} \geq 121) \\&+ X_{it}'\lambda + \eta_s + \tau_t + u_{ist}\end{aligned} \]
where:
\(\hat{QWS}_{ist}\) = Instrumented proportion of licensed workers.
\(\gamma_1\) = Causal effect of certified staffing on quality outcomes.
Key Observations
- The larger the discontinuity at 120 beds, the closer \(\gamma_1 \approx \beta_1\).
- The ITT effect (\(\beta_1\)) will always be weaker than the local average treatment effect (\(\gamma_1\)).
27.13.4.6 Empirical Challenges
-
Bunching at Round Numbers:
- Figure 1 shows facilities clustering at every 5-bed increment.
- If manipulation occurs, we expect underrepresentation at 130 beds.
-
Clustering Standard Errors:
- Due to limited unique mass points (facilities at specific sizes), errors should be clustered by mass point instead of individual facilities.
-
Noncompliance and Selection Bias:
- Fuzzy RD requires that we do not drop non-compliers (as it would introduce selection bias).
- However, we can drop manipulators if there is clear evidence of behavioral bias (e.g., preference for round numbers).