26.7 Design vs. Model-Based Approaches
Quasi-experimental methods exist along a spectrum between design-based and model-based approaches, rather than fitting neatly into one category or the other. At one end, the design-based perspective emphasizes study structure, aiming to approximate randomization through external sources of variation, such as policy changes or natural experiments. At the other end, the model-based perspective relies more heavily on statistical assumptions and functional forms to estimate causal relationships.
Most quasi-experimental methods blend elements of both perspectives, differing in the degree to which they prioritize design validity over statistical modeling. This section explores the continuum of these approaches, highlighting their fundamental differences and implications for empirical research.
See Figure 26.3 for a visual spectrum, positioning common quasi-experimental methods along the continuum from design-based to model-based.
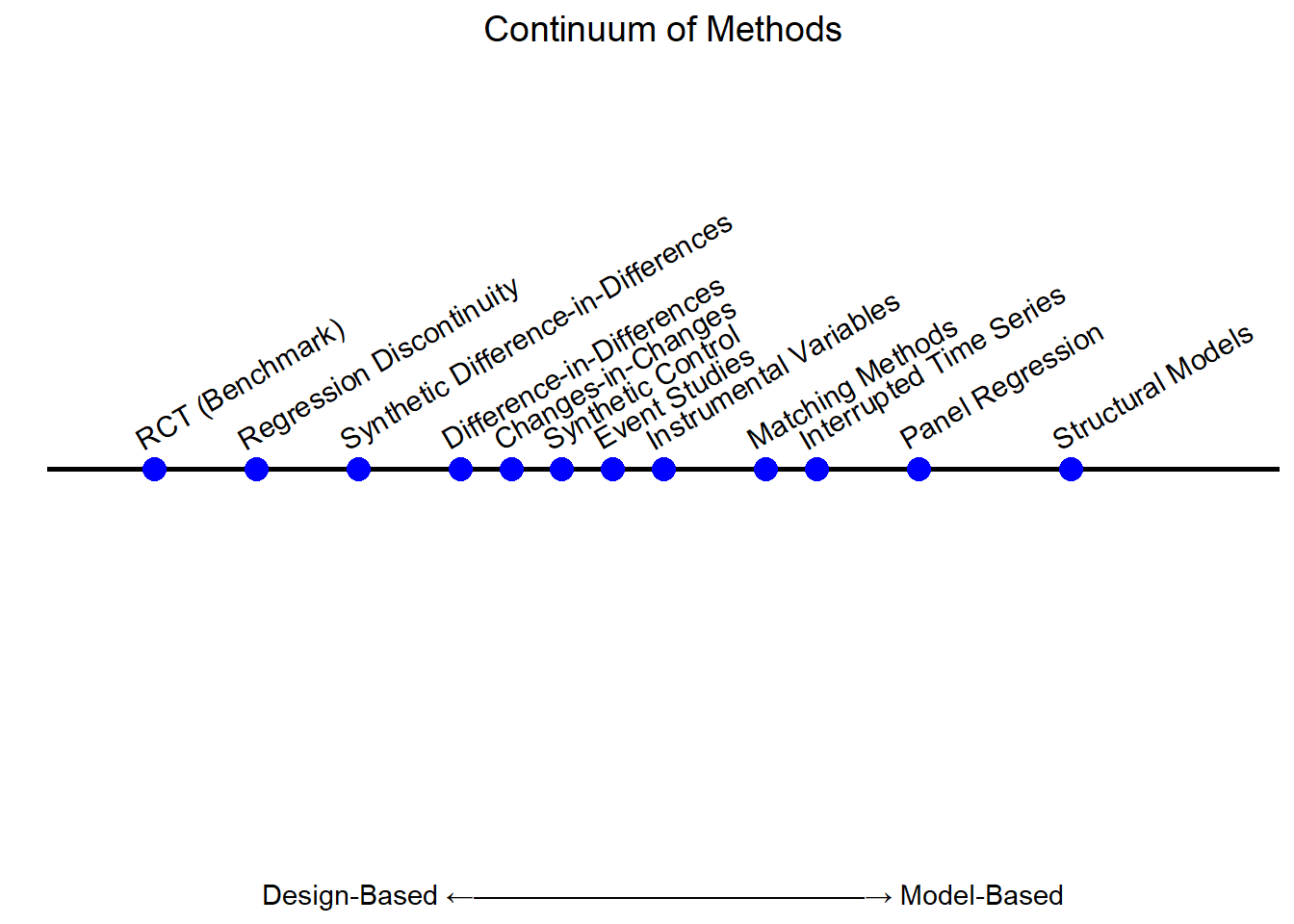
Figure 26.3: Continuum of Causal Inference Methods
- Design-Based Causal Inference:
Focuses on using the design of the study or experiment to establish causal relationships.
Relies heavily on randomization, natural experiments, and quasi-experimental designs (e.g., Difference-in-Differences, Regression Discontinuity, Instrumental Variables).
Assumes that well-designed studies or natural experiments produce plausibly exogenous variation in the treatment, minimizing reliance on strong modeling assumptions.
Emphasizes transparency in how the treatment assignment mechanism isolates causal effects.
- Model-Based Causal Inference:
Relies on explicit statistical models to infer causality, typically grounded in theory and assumptions about the data-generating process.
Commonly uses structural equation models, propensity score models, and frameworks like Bayesian inference.
Assumptions are crucial (e.g., no omitted variable bias, correct model specification, ignorability).
May be employed when experimental or quasi-experimental designs are not feasible.
| Aspect | Design-Based | Model-Based |
|---|---|---|
| Approach | Relies on study design | Relies on statistical models |
| Assumptions | Fewer, often intuitive (e.g., cutoff) | Stronger, often less testable |
| Examples | RCTs, natural experiments, RD, DiD | Structural models, PSM |
| Strengths | Transparent, robust to misspecification | Useful when design is not possible |
| Weaknesses | Limited generalizability, context-specific | Sensitive to assumptions |
Both streams are complementary, and often, researchers combine elements of both to robustly estimate causal effects (i.e., multi-method studies). For example, a design-based approach might be supplemented with a model-based framework to address specific limitations like imperfect randomization (Table 26.8).
26.7.1 Design-Based Perspective
The design-based perspective in causal inference emphasizes exploiting natural sources of variation that approximate randomization (Table 26.9). Unlike structural models, which rely on extensive theoretical assumptions, design-based methods leverage exogenous events, policy changes, or assignment rules to infer causal effects with minimal modeling assumptions.
These methods are particularly useful when:
Randomized controlled trials are infeasible, unethical, or impractical.
Treatment assignment is plausibly exogenous due to a policy, threshold, or external shock.
Quasi-random variation exists (e.g., firms, consumers, or individuals are assigned treatment based on factors outside their control).
| Method | Key Concept | Assumptions | Example (Marketing & Economics) |
|---|---|---|---|
| Regression Discontinuity | Units near a threshold are as good as random. | No precise control over cutoff; outcomes continuous. | Loyalty program tiers, minimum wage effects. |
| Synthetic Control | Constructs a weighted synthetic counterfactual. | Pre-treatment trends must match; no confounding post-treatment shocks. | National ad campaign impact, tax cut effects. |
| Event Studies | Measures how an event changes outcomes over time. | Parallel pre-trends; no anticipatory effects. | Black Friday sales, stock price reactions. |
| Matching Methods | Matches similar treated & untreated units. | Selection on observables; common support. | Ad exposure vs. non-exposure, education & earnings. |
| Instrumental Variables | Uses an exogenous variable to mimic randomization. | Instrument must be relevant; must not affect outcomes directly. | Ad regulations as IV for ad exposure, lottery-based college admissions. |
26.7.2 Model-Based Perspective
The model-based perspective in causal inference relies on statistical modeling techniques to estimate treatment effects, rather than exploiting exogenous sources of variation as in design-based approaches. In this framework, researchers explicitly specify relationships between variables, using mathematical models to control for confounding and estimate counterfactual outcomes (Table 26.10).
Unlike other quasi-experimental designs that leverage external assignment mechanisms (e.g., a cutoff, policy change, or natural experiment), model-based methods assume that confounding can be adequately adjusted for using statistical techniques alone. This makes them highly flexible but also more vulnerable to model misspecification and omitted variable bias.
Key Characteristics of Model-Based Approaches
Dependence on Correct Model Specification
The validity of causal estimates hinges on the correct functional form of the model.
If the model is misspecified (e.g., incorrect interactions, omitted variables), bias can arise.
No Need for Exogenous Variation
Unlike design-based methods, model-based approaches do not rely on policy shocks, thresholds, or instrumental variables.
Instead, they estimate causal effects entirely through statistical modeling.
Assumption of Ignorability
These methods assume that all relevant confounders are observed and properly included in the model.
This assumption is untestable and may be violated in practice, leading to biased estimates.
Flexibility and Generalizability
Model-based methods allow researchers to estimate treatment effects even when exogenous variation is unavailable.
They can be applied in a wide range of settings where policy-driven variation does not exist.
| Method | Key Concept | Assumptions | Example (Marketing & Economics) |
|---|---|---|---|
| Propensity Score Matching (PSM) / Weighting | Uses estimated probabilities of treatment to create comparable groups. | Treatment assignment is modeled correctly; no unmeasured confounding. | Job training programs (matching participants to non-participants); Ad campaign exposure. |
| Structural Causal Models (SCMs) / DAGs | Specifies causal relationships using directed acyclic graphs (DAGs). | Correct causal structure; no omitted paths. | Customer churn prediction; Impact of pricing on sales. |
| Covariate Adjustment (Regression-Based Approaches) | Uses regression to control for confounding variables. | Linear or nonlinear functional forms are correctly specified. | Estimating the impact of online ads on revenue. |
| Machine Learning for Causal Inference | Uses ML algorithms (e.g., causal forests, BART) to estimate treatment effects. | Assumes data-driven methods can capture complex relationships. | Personalized marketing campaigns; Predicting loan default rates. |
26.7.2.1 Propensity Score Matching and Weighting
Propensity Score Matching estimates the probability of treatment assignment based on observed characteristics, then matches treated and control units with similar probabilities to mimic randomization.
Key Assumptions
Correct Model Specification: The propensity score model (typically a logistic regression) must correctly capture all relevant covariates affecting treatment assignment.
Ignorability: There are no unmeasured confounders. All relevant differences between treated and control groups are accounted for.
Why It’s Model-Based
Unlike design-based methods, which exploit external sources of variation, PSM depends entirely on the statistical model to balance covariates.
Any mis-specification in the propensity score model can introduce bias.
Examples
Marketing: Evaluating the impact of targeted advertising on purchase behavior by matching customers exposed to an ad with unexposed customers who have similar browsing histories.
Economics: Estimating the effect of job training programs on income by matching participants with non-participants based on demographic and employment history.
26.7.2.2 Structural Causal Models and Directed Acyclic Graphs
SCMs provide a mathematical framework to represent causal relationships using structural equations and directed acyclic graphs (DAGs). These models explicitly encode assumptions about how variables influence each other.
Key Assumptions
Correct DAG Specification: The researcher must correctly specify the causal graph structure.
Exclusion Restrictions: Some variables must only affect outcomes through specified causal pathways.
Why It’s Model-Based
SCMs require explicit causal assumptions, unlike design-based approaches that rely on external assignments.
Identification depends on structural equations, which can be misspecified.
Examples
Marketing: Modeling the causal impact of pricing strategies on sales while accounting for advertising, competitor actions, and seasonal effects.
Economics: Estimating the effect of education on wages, considering the impact of family background, school quality, and job market conditions.
Covariate Adjustment (Regression-Based Approaches)
Regression models estimate causal effects by controlling for observed confounders. This includes linear regression, logistic regression, and more flexible models like generalized additive models (GAMs).
Key Assumptions
Linear or Nonlinear Functional Form Must Be Correct.
No Omitted Variable Bias: All relevant confounders must be measured and included.
Why It’s Model-Based
Estimates depend entirely on the correctness of the model form and covariates included.
Unlike design-based methods, there is no exogenous source of variation.
Examples
Marketing: Estimating the effect of social media ads on conversions while controlling for past purchase behavior and customer demographics.
Economics: Evaluating the impact of financial aid on student performance, adjusting for prior academic records.
26.7.2.3 Machine Learning for Causal Inference
Machine learning (ML) techniques, such as causal forests, Bayesian Additive Regression Trees (BART), and double machine learning (DML), provide flexible methods for estimating treatment effects without strict functional form assumptions.
Key Assumptions
Sufficient Training Data: ML models require large datasets to capture treatment heterogeneity.
Algorithm Interpretability: Unlike standard regression, ML-based causal inference can be harder to interpret.
Why It’s Model-Based
Relies on statistical learning algorithms rather than external assignment mechanisms.
Identification depends on data-driven feature selection, not a policy design.
Examples
Marketing: Predicting individualized treatment effects of ad targeting using causal forests.
Economics: Estimating heterogeneous effects of tax incentives on business investment.
26.7.3 Placing Methods Along a Spectrum
In reality, each method balances these two philosophies differently:
Strongly Design-Based: Randomized Controlled Trials, clear natural experiments (e.g., lotteries), or near-random assignment rules (RD near the threshold).
Hybrid / Semi-Design Approaches: Difference-in-Differences, Synthetic Control, many matching approaches (they rely on credible assumptions or designs but often still need modeling choices, e.g., functional form for trends).
Strongly Model-Based: Structural equation models (SCMs), certain propensity score approaches, Bayesian causal inference with a fully specified likelihood, etc.
Hence, the key question for each method is:
“How much is identification relying on the ‘as-good-as-random’ design versus how much on structural or statistical modeling assumptions?”
If you can argue the variation in treatment is practically random (or near-random) from a design standpoint, you’re leaning toward the design-based camp.
If your identification crucially depends on specifying a correct model or having strong assumptions about the data-generating process, you’re more in the model-based camp.
Most real-world applications lie somewhere in the middle, combining aspects of both approaches (Table 26.11.
| Feature | Design-Based Perspective | Model-Based Perspective |
|---|---|---|
| Causal Identification | Based on external design (e.g., policy, cutoff, exogenous event). | Based on statistical modeling of treatment assignment. |
| Reliance on Exogeneity | Yes, due to natural variation in treatment assignment. | No, relies on observed data adjustments. |
| Control for Confounders | Partially through design (e.g., RD exploits cutoffs). | Entirely through covariate control. |
| Handling of Unobserved Confounders | Often addressed through design assumptions. | Assumes ignorability (no unobserved confounders). |
| Examples | RD, DiD, IV, Synthetic Control. | PSM, DAGs, Regression-Based, ML-Based Causal Inference. |