4.1 Hypothesis Testing Framework
Hypothesis testing is one of the fundamental tools in statistics. It provides a formal procedure to test claims or assumptions (hypotheses) about population parameters using sample data. This process is essential in various fields, including business, medicine, and social sciences, as it helps answer questions like “Does a new marketing strategy improve sales?” or “Is there a significant difference in test scores between two teaching methods?”
The goal of hypothesis testing is to make decisions or draw conclusions about a population based on sample data. This is necessary because we rarely have access to the entire population. For example, if a company wants to determine whether a new advertising campaign increases sales, it might analyze data from a sample of stores rather than every store globally.
Key Steps in Hypothesis Testing
- Formulate Hypotheses: Define the null and alternative hypotheses.
- Choose a Significance Level (\(\alpha\)): Determine the acceptable probability of making a Type I error.
- Select a Test Statistic: Identify the appropriate statistical test based on the data and hypotheses.
- Define the Rejection Region: Specify the range of values for which the null hypothesis will be rejected.
- Compute the Test Statistic: Use sample data to calculate the test statistic.
- Make a Decision: Compare the test statistic to the critical value or use the p-value to decide whether to reject or fail to reject the null hypothesis.
4.1.1 Null and Alternative Hypotheses
At the heart of hypothesis testing lies the formulation of two competing hypotheses:
- Null Hypothesis (\(H_0\)):
- Represents the current state of knowledge, status quo, or no effect.
- It is assumed true unless there is strong evidence against it.
- Examples:
- \(H_0: \mu_1 = \mu_2\) (no difference in means between two groups).
- \(H_0: \beta = 0\) (a predictor variable has no effect in a regression model).
- Think of \(H_0\) as the “default assumption.”
- Alternative Hypothesis (\(H_a\) or \(H_1\)):
- Represents a claim that contradicts the null hypothesis.
- It is what you are trying to prove or find evidence for.
- Examples:
- \(H_a: \mu_1 \neq \mu_2\) (means of two groups are different).
- \(H_a: \beta \neq 0\) (a predictor variable has an effect).
4.1.2 Errors in Hypothesis Testing
Hypothesis testing involves decision-making under uncertainty, meaning there is always a risk of making errors. These errors are classified into two types:
- Type I Error (\(\alpha\)):
- Occurs when the null hypothesis is rejected, even though it is true.
- Example: Concluding that a medication is effective when it actually has no effect.
- The probability of making a Type I error is denoted by \(\alpha\), called the significance level (commonly set at 0.05 or 5%).
- Type II Error (\(\beta\)):
- Occurs when the null hypothesis is not rejected, but the alternative hypothesis is true.
- Example: Failing to detect that a medication is effective when it actually works.
- The complement of \(\beta\) is called the power of the test (\(1 - \beta\)), representing the probability of correctly rejecting the null hypothesis.
Analogy: The Legal System
To make this concept more intuitive, consider the analogy of a courtroom:
- Null Hypothesis (\(H_0\)): The defendant is innocent.
- Alternative Hypothesis (\(H_a\)): The defendant is guilty.
- Type I Error: Convicting an innocent person (false positive).
- Type II Error: Letting a guilty person go free (false negative).
Balancing \(\alpha\) and \(\beta\) is critical in hypothesis testing, as reducing one often increases the other. For example, if you make it harder to reject \(H_0\) (reducing \(\alpha\)), you increase the chance of failing to detect a true effect (increasing \(\beta\)).
4.1.3 The Role of Distributions in Hypothesis Testing
Distributions play a fundamental role in hypothesis testing because they provide a mathematical model for understanding how a test statistic behaves under the null hypothesis (\(H_0\)). Without distributions, it would be impossible to determine whether the observed results are due to random chance or provide evidence to reject the null hypothesis.
4.1.3.1 Expected Outcomes
One of the key reasons distributions are so crucial is that they describe the range of values a test statistic is likely to take when \(H_0\) is true. This helps us understand what is considered “normal” variation in the data due to random chance. For example:
- Imagine you are conducting a study to test whether a new marketing strategy increases the average monthly sales. Under the null hypothesis, you assume the new strategy has no effect, and the average sales remain unchanged.
- When you collect a sample and calculate the test statistic, you compare it to the expected distribution (e.g., the normal distribution for a \(z\)-test). This distribution shows the range of test statistic values that are likely to occur purely due to random fluctuations in the data, assuming \(H_0\) is true.
By providing this baseline of what is “normal,” distributions allow us to identify unusual results that may indicate the null hypothesis is false.
4.1.3.2 Critical Values and Rejection Regions
Distributions also help define critical values and rejection regions in hypothesis testing. Critical values are specific points on the distribution that mark the boundaries of the rejection region. The rejection region is the range of values for the test statistic that lead us to reject \(H_0\).
The location of these critical values depends on:
The level of significance (\(\alpha\)), which is the probability of rejecting \(H_0\) when it is true (a Type I error).
The shape of the test statistic’s distribution under \(H_0\).
For example:
- In a one-tailed \(z\)-test with \(\alpha = 0.05\), the critical value is approximately \(1.645\) for a standard normal distribution. If the calculated test statistic exceeds this value, we reject \(H_0\) because such a result would be very unlikely under \(H_0\).
Distributions help us visually and mathematically determine these critical points. By examining the distribution, we can see where the rejection region lies and what the probability is of observing a value in that region by random chance alone.
4.1.3.3 P-values
The p-value, a central concept in hypothesis testing, is directly derived from the distribution of the test statistic under \(H_0\). The p-value represents the probability of observing a test statistic as extreme as (or more extreme than) the one calculated, assuming \(H_0\) is true.
The p-value quantifies the strength of evidence against \(H_0\). It represents the probability of observing a test statistic as extreme as (or more extreme than) the one calculated, assuming \(H_0\) is true.
- Small p-value (< \(\alpha\)): Strong evidence against \(H_0\); reject \(H_0\).
- Large p-value (> \(\alpha\)): Weak evidence against \(H_0\); fail to reject \(H_0\).
For example:
Suppose you calculate a \(z\)-test statistic of \(2.1\) in a one-tailed test. Using the standard normal distribution, the p-value is the area under the curve to the right of \(z = 2.1\). This area represents the likelihood of observing a result as extreme as \(z = 2.1\) if \(H_0\) is true.
In this case, the p-value is approximately \(0.0179\). A small p-value (typically less than \(\alpha = 0.05\)) suggests that the observed result is unlikely under \(H_0\) and provides evidence to reject the null hypothesis.
4.1.3.4 Why Does All This Matter?
To summarize, distributions are the backbone of hypothesis testing because they allow us to:
Define what is expected under \(H_0\) by modeling the behavior of the test statistic.
Identify results that are unlikely to occur by random chance, which leads to the rejection of \(H_0\).
Calculate p-values to quantify the strength of evidence against \(H_0\).
Distributions provide the framework for understanding the role of chance in statistical analysis. They are essential for determining expected outcomes, setting thresholds for decision-making (critical values and rejection regions), and calculating p-values. A solid grasp of distributions will greatly enhance your ability to interpret and conduct hypothesis tests, making it easier to draw meaningful conclusions from data.
4.1.4 The Test Statistic
The test statistic is a crucial component in hypothesis testing, as it quantifies how far the observed data deviates from what we would expect if the null hypothesis (\(H_0\)) were true. Essentially, it provides a standardized way to compare the observed outcomes against the expectations set by \(H_0\), enabling us to assess whether the observed results are likely due to random chance or indicative of a significant effect.
The general formula for a test statistic is:
\[ \text{Test Statistic} = \frac{\text{Observed Value} - \text{Expected Value under } H_0}{\text{Standard Error}} \]
Each component of this formula has an important role:
- Numerator:
- The numerator represents the difference between the actual data (observed value) and the hypothetical value (expected value) that is assumed under \(H_0\).
- This difference quantifies the extent of the deviation. A larger deviation suggests stronger evidence against \(H_0\).
- Denominator:
- The denominator is the standard error, which measures the variability or spread of the data. It accounts for factors such as sample size and the inherent randomness of the data.
- By dividing the numerator by the standard error, the test statistic is standardized, allowing comparisons across different studies, sample sizes, and distributions.
The test statistic plays a central role in determining whether to reject \(H_0\). Once calculated, it is compared to a known distribution (e.g., standard normal distribution for \(z\)-tests or \(t\)-distribution for \(t\)-tests). This comparison allows us to evaluate the likelihood of observing such a test statistic under \(H_0\):
- If the test statistic is close to 0: This indicates that the observed data is very close to what is expected under \(H_0\). There is little evidence to suggest rejecting \(H_0\).
- If the test statistic is far from 0 (in the tails of the distribution): This suggests that the observed data deviates significantly from the expectations under \(H_0\). Such deviations may provide strong evidence against \(H_0\).
4.1.4.1 Why Standardizing Matters
Standardizing the difference between the observed and expected values ensures that the test statistic is not biased by factors such as the scale of measurement or the size of the sample. For instance:
A raw difference of 5 might be highly significant in one context but negligible in another, depending on the variability (standard error).
Standardizing ensures that the magnitude of the test statistic reflects both the size of the difference and the reliability of the sample data.
4.1.4.2 Interpreting the Test Statistic
After calculating the test statistic, it is used to:
- Compare with a critical value: For example, in a \(z\)-test with \(\alpha = 0.05\), the critical values are \(-1.96\) and \(1.96\) for a two-tailed test. If the test statistic falls beyond these values, \(H_0\) is rejected.
- Calculate the p-value: The p-value is derived from the distribution and reflects the probability of observing a test statistic as extreme as the one calculated if \(H_0\) is true.
4.1.5 Critical Values and Rejection Regions
The critical value is a point on the distribution that separates the rejection region from the non-rejection region:
- Rejection Region: If the test statistic falls in this region, we reject \(H_0\).
- Non-Rejection Region: If the test statistic falls here, we fail to reject \(H_0\).
The rejection region depends on the significance level (\(\alpha\)). For a two-tailed test with \(\alpha = 0.05\), the critical values correspond to the top 2.5% and bottom 2.5% of the distribution.
4.1.6 Visualizing Hypothesis Testing
Let’s create a visualization to tie these concepts together:
# Parameters
alpha <- 0.05 # Significance level
df <- 29 # Degrees of freedom (for t-distribution)
t_critical <-
qt(1 - alpha / 2, df) # Critical value for two-tailed test
# Generate t-distribution values
t_values <- seq(-4, 4, length.out = 1000)
density <- dt(t_values, df)
# Observed test statistic
t_obs <- 2.5 # Example observed test statistic
# Plot the t-distribution
plot(
t_values,
density,
type = "l",
lwd = 2,
col = "blue",
main = "Hypothesis Testing with Distribution",
xlab = "Test Statistic (t-value)",
ylab = "Density",
ylim = c(0, 0.4)
)
# Shade the rejection regions
polygon(c(t_values[t_values <= -t_critical], -t_critical),
c(density[t_values <= -t_critical], 0),
col = "red",
border = NA)
polygon(c(t_values[t_values >= t_critical], t_critical),
c(density[t_values >= t_critical], 0),
col = "red",
border = NA)
# Add observed test statistic
points(
t_obs,
dt(t_obs, df),
col = "green",
pch = 19,
cex = 1.5
)
text(
t_obs,
dt(t_obs, df) + 0.02,
paste("Observed t:", round(t_obs, 2)),
col = "green",
pos = 3
)
# Highlight the critical values
abline(
v = c(-t_critical, t_critical),
col = "black",
lty = 2
)
text(
-t_critical,
0.05,
paste("Critical Value:", round(-t_critical, 2)),
pos = 4,
col = "black"
)
text(
t_critical,
0.05,
paste("Critical Value:", round(t_critical, 2)),
pos = 4,
col = "black"
)
# Calculate p-value
p_value <- 2 * (1 - pt(abs(t_obs), df)) # Two-tailed p-value
text(0,
0.35,
paste("P-value:", round(p_value, 4)),
col = "blue",
pos = 3)
# Annotate regions
text(-3,
0.15,
"Rejection Region",
col = "red",
pos = 3)
text(3, 0.15, "Rejection Region", col = "red", pos = 3)
text(0,
0.05,
"Non-Rejection Region",
col = "blue",
pos = 3)
# Add legend
legend(
"topright",
legend = c("Rejection Region", "Critical Value", "Observed Test Statistic"),
col = c("red", "black", "green"),
lty = c(NA, 2, NA),
pch = c(15, NA, 19),
bty = "n"
)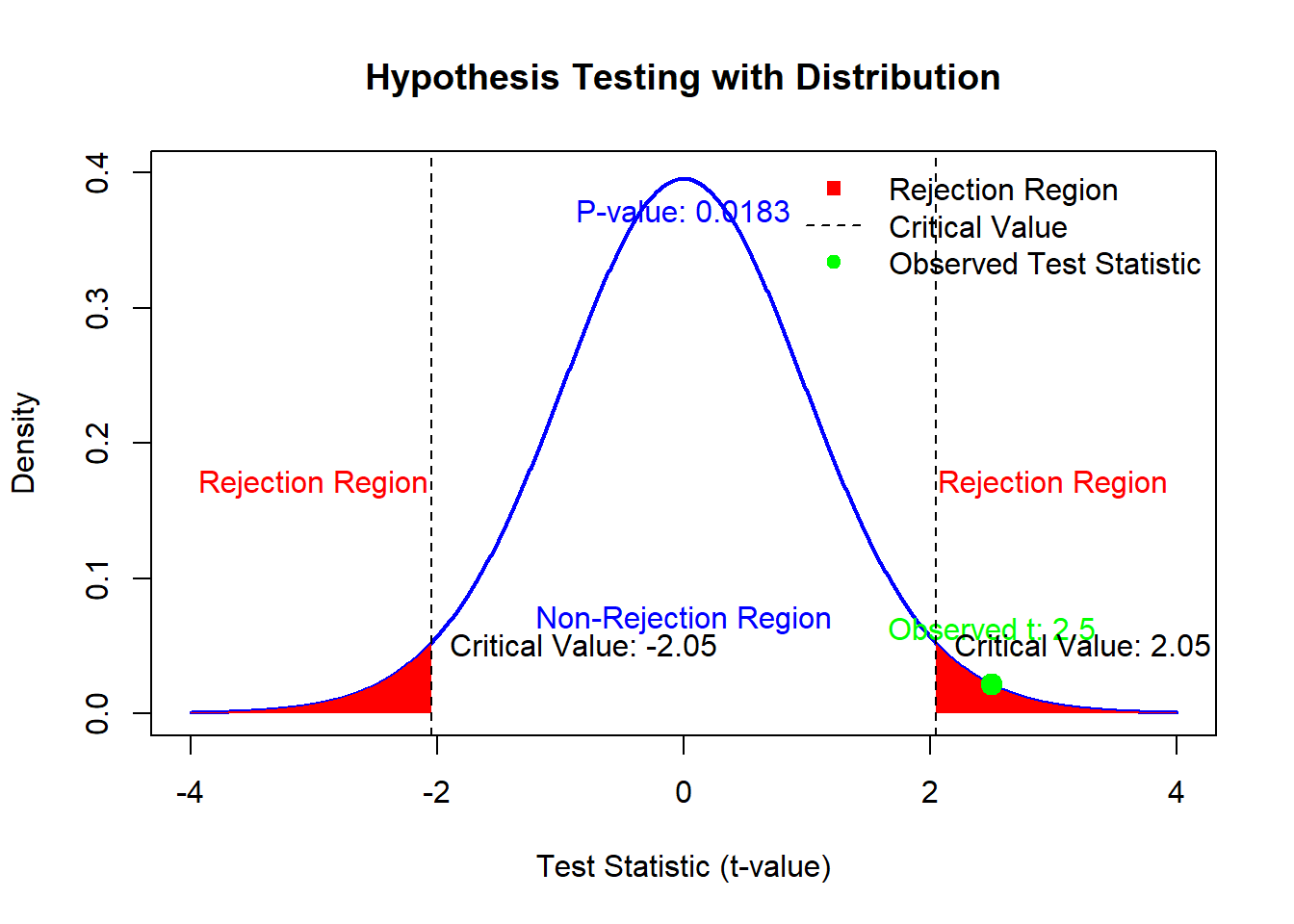
Figure 2.1: Hypothesis Testing with Distribution