19.2 Causal Inference Approach to Mediation
Traditional mediation models assume that regression-based estimates provide valid causal inference. However, causal mediation analysis (CMA) extends beyond traditional models by explicitly defining mediation in terms of potential outcomes and counterfactuals.
19.2.1 Example: Traditional Mediation Analysis
We begin with a classic three-step mediation approach.
# Load data
myData <- read.csv("data/mediationData.csv")
# Step 1 (Total Effect: X → Y) [No longer required]
model.0 <- lm(Y ~ X, data = myData)
summary(model.0)
#>
#> Call:
#> lm(formula = Y ~ X, data = myData)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -5.0262 -1.2340 -0.3282 1.5583 5.1622
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 2.8572 0.6932 4.122 7.88e-05 ***
#> X 0.3961 0.1112 3.564 0.000567 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 1.929 on 98 degrees of freedom
#> Multiple R-squared: 0.1147, Adjusted R-squared: 0.1057
#> F-statistic: 12.7 on 1 and 98 DF, p-value: 0.0005671
# Step 2 (Effect of X on M)
model.M <- lm(M ~ X, data = myData)
summary(model.M)
#>
#> Call:
#> lm(formula = M ~ X, data = myData)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -4.3046 -0.8656 0.1344 1.1344 4.6954
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 1.49952 0.58920 2.545 0.0125 *
#> X 0.56102 0.09448 5.938 4.39e-08 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 1.639 on 98 degrees of freedom
#> Multiple R-squared: 0.2646, Adjusted R-squared: 0.2571
#> F-statistic: 35.26 on 1 and 98 DF, p-value: 4.391e-08
# Step 3 (Effect of M on Y, controlling for X)
model.Y <- lm(Y ~ X + M, data = myData)
summary(model.Y)
#>
#> Call:
#> lm(formula = Y ~ X + M, data = myData)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -3.7631 -1.2393 0.0308 1.0832 4.0055
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 1.9043 0.6055 3.145 0.0022 **
#> X 0.0396 0.1096 0.361 0.7187
#> M 0.6355 0.1005 6.321 7.92e-09 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 1.631 on 97 degrees of freedom
#> Multiple R-squared: 0.373, Adjusted R-squared: 0.3601
#> F-statistic: 28.85 on 2 and 97 DF, p-value: 1.471e-10
# Step 4: Bootstrapping for ACME
library(mediation)
results <-
mediate(
model.M,
model.Y,
treat = 'X',
mediator = 'M',
boot = TRUE,
sims = 500
)
summary(results)
#>
#> Causal Mediation Analysis
#>
#> Nonparametric Bootstrap Confidence Intervals with the Percentile Method
#>
#> Estimate 95% CI Lower 95% CI Upper p-value
#> ACME 0.356522 0.211871 0.507799 <2e-16 ***
#> ADE 0.039604 -0.174982 0.278427 0.760
#> Total Effect 0.396126 0.174283 0.643540 0.004 **
#> Prop. Mediated 0.900022 0.504160 1.937520 0.004 **
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Sample Size Used: 100
#>
#>
#> Simulations: 500- Total Effect: \(\hat{c} = 0.3961\) → effect of \(X\) on \(Y\) without controlling for \(M\).
- Direct Effect (ADE): \(\hat{c'} = 0.0396\) → effect of \(X\) on \(Y\) after accounting for \(M\).
- ACME (Average Causal Mediation Effect):
ACME = \(\hat{c} - \hat{c'} = 0.3961 - 0.0396 = 0.3565\)
Equivalent to product of paths: \(\hat{a} \times \hat{b} = 0.56102 \times 0.6355 = 0.3565\).
These calculations do not rely on strong causal assumptions. For a causal interpretation, we need a more rigorous framework.
19.2.2 Two Approaches in Causal Mediation Analysis
The mediation package Imai, Keele, and Yamamoto (2010) enables causal mediation analysis. It supports two inference types:
Model-Based Inference
Assumptions:
Treatment is randomized (or approximated via matching).
Sequential Ignorability: No unobserved confounding in:
Treatment → Mediator
Treatment → Outcome
Mediator → Outcome
This assumption is hard to justify in observational studies.
Design-Based Inference
- Relies on experimental design to isolate the causal mechanism.
Notation
We follow the standard potential outcomes framework:
\(M_i(t)\) = mediator under treatment condition \(t\)
\(T_i \in {0,1}\) = treatment assignment
\(Y_i(t, m)\) = outcome under treatment \(t\) and mediator value \(m\)
\(X_i\) = observed pre-treatment covariates
The treatment effect for an individual \(i\): \[ \tau_i = Y_i(1,M_i(1)) - Y_i (0,M_i(0)) \] which decomposes into:
- Causal Mediation Effect (ACME):
\[ \delta_i (t) = Y_i (t,M_i(1)) - Y_i(t,M_i(0)) \]
- Direct Effect (ADE):
\[ \zeta_i (t) = Y_i (1, M_i(1)) - Y_i(0, M_i(0)) \]
Summing up:
\[ \tau_i = \delta_i (t) + \zeta_i (1-t) \]
Sequential Ignorability Assumption
For CMA to be valid, we assume:
\[ \begin{aligned} \{ Y_i (t', m), M_i (t) \} &\perp T_i |X_i = x\\ Y_i(t',m) &\perp M_i(t) | T_i = t, X_i = x \end{aligned} \]
First condition is the standard strong ignorability condition where treatment assignment is random conditional on pre-treatment confounders.
Second condition is stronger where the mediators is also random given the observed treatment and pre-treatment confounders. This condition is satisfied only when there is no unobserved pre-treatment confounders, and post-treatment confounders, and multiple mediators that are correlated.
Key Challenge
Sequential Ignorability is not testable. Researchers should conduct sensitivity analysis.
We now fit a causal mediation model using mediation.
library(mediation)
set.seed(2014)
data("framing", package = "mediation")
# Step 1: Fit mediator model (M ~ T, X)
med.fit <-
lm(emo ~ treat + age + educ + gender + income, data = framing)
# Step 2: Fit outcome model (Y ~ M, T, X)
out.fit <-
glm(
cong_mesg ~ emo + treat + age + educ + gender + income,
data = framing,
family = binomial("probit")
)
# Step 3: Causal Mediation Analysis (Quasi-Bayesian)
med.out <-
mediate(
med.fit,
out.fit,
treat = "treat",
mediator = "emo",
robustSE = TRUE,
sims = 100
) # Use sims = 10000 in practice
summary(med.out)
#>
#> Causal Mediation Analysis
#>
#> Quasi-Bayesian Confidence Intervals
#>
#> Estimate 95% CI Lower 95% CI Upper p-value
#> ACME (control) 0.079128 0.035058 0.150095 <2e-16 ***
#> ACME (treated) 0.080385 0.036654 0.155707 <2e-16 ***
#> ADE (control) 0.020551 -0.097597 0.115775 0.70
#> ADE (treated) 0.021808 -0.105256 0.122624 0.70
#> Total Effect 0.100936 -0.049706 0.233869 0.14
#> Prop. Mediated (control) 0.694620 -6.310861 3.679318 0.14
#> Prop. Mediated (treated) 0.711848 -5.793642 3.496550 0.14
#> ACME (average) 0.079756 0.035856 0.153702 <2e-16 ***
#> ADE (average) 0.021180 -0.101427 0.119199 0.70
#> Prop. Mediated (average) 0.703234 -6.052251 3.587934 0.14
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Sample Size Used: 265
#>
#>
#> Simulations: 100Alternative: Nonparametric Bootstrap
med.out <-
mediate(
med.fit,
out.fit,
boot = TRUE,
treat = "treat",
mediator = "emo",
sims = 100,
boot.ci.type = "bca"
)
summary(med.out)
#>
#> Causal Mediation Analysis
#>
#> Nonparametric Bootstrap Confidence Intervals with the BCa Method
#>
#> Estimate 95% CI Lower 95% CI Upper p-value
#> ACME (control) 0.084786 0.042409 0.135927 <2e-16 ***
#> ACME (treated) 0.085820 0.041012 0.136296 <2e-16 ***
#> ADE (control) 0.011654 -0.072556 0.133438 0.58
#> ADE (treated) 0.012689 -0.078400 0.141850 0.58
#> Total Effect 0.097475 0.012219 0.249860 0.06 .
#> Prop. Mediated (control) 0.869822 1.746034 151.198626 0.06 .
#> Prop. Mediated (treated) 0.880437 1.687950 138.906093 0.06 .
#> ACME (average) 0.085303 0.043380 0.137194 <2e-16 ***
#> ADE (average) 0.012172 -0.075578 0.137570 0.58
#> Prop. Mediated (average) 0.875130 1.716992 145.052358 0.06 .
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Sample Size Used: 265
#>
#>
#> Simulations: 100If we suspect moderation, we include an interaction term.
med.fit <-
lm(emo ~ treat + age + educ + gender + income, data = framing)
out.fit <-
glm(
cong_mesg ~ emo * treat + age + educ + gender + income,
data = framing,
family = binomial("probit")
)
med.out <-
mediate(
med.fit,
out.fit,
treat = "treat",
mediator = "emo",
robustSE = TRUE,
sims = 100
)
summary(med.out)
#>
#> Causal Mediation Analysis
#>
#> Quasi-Bayesian Confidence Intervals
#>
#> Estimate 95% CI Lower 95% CI Upper p-value
#> ACME (control) 0.0741675 0.0240117 0.1364901 <2e-16 ***
#> ACME (treated) 0.0949636 0.0270237 0.1630112 <2e-16 ***
#> ADE (control) -0.0135332 -0.1185510 0.1096060 0.76
#> ADE (treated) 0.0072629 -0.1100691 0.1145408 0.90
#> Total Effect 0.0814304 -0.0564589 0.1924589 0.26
#> Prop. Mediated (control) 0.6451040 -14.3124300 3.1336595 0.26
#> Prop. Mediated (treated) 0.9800632 -17.8320223 4.0060277 0.26
#> ACME (average) 0.0845655 0.0273792 0.1470397 <2e-16 ***
#> ADE (average) -0.0031352 -0.1145684 0.1172708 1.00
#> Prop. Mediated (average) 0.8125836 -16.0722261 3.5478494 0.26
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Sample Size Used: 265
#>
#>
#> Simulations: 100
test.TMint(med.out, conf.level = .95) # Tests for interaction effect
#>
#> Test of ACME(1) - ACME(0) = 0
#>
#> data: estimates from med.out
#> ACME(1) - ACME(0) = 0.020796, p-value = 0.3
#> alternative hypothesis: true ACME(1) - ACME(0) is not equal to 0
#> 95 percent confidence interval:
#> -0.01757310 0.07110837Since sequential ignorability is untestable, we examine how unmeasured confounding affects ACME estimates.
# Load required package
library(mediation)
# Simulate some example data
set.seed(123)
n <- 100
data <- data.frame(
treat = rbinom(n, 1, 0.5), # Binary treatment
med = rnorm(n), # Continuous mediator
outcome = rnorm(n) # Continuous outcome
)
# Fit the mediator model (med ~ treat)
med_model <- lm(med ~ treat, data = data)
# Fit the outcome model (outcome ~ treat + med)
outcome_model <- lm(outcome ~ treat + med, data = data)
# Perform mediation analysis
med_out <- mediate(med_model,
outcome_model,
treat = "treat",
mediator = "med",
sims = 100)
# Conduct sensitivity analysis
sens_out <- medsens(med_out, sims = 100)
summary(sens_out)
#>
#> Mediation Sensitivity Analysis for Average Causal Mediation Effect
#>
#> Sensitivity Region
#>
#> Rho ACME 95% CI Lower 95% CI Upper R^2_M*R^2_Y* R^2_M~R^2_Y~
#> [1,] -0.9 -0.6194 -1.3431 0.1043 0.81 0.7807
#> [2,] -0.8 -0.3898 -0.8479 0.0682 0.64 0.6168
#> [3,] -0.7 -0.2790 -0.6096 0.0516 0.49 0.4723
#> [4,] -0.6 -0.2067 -0.4552 0.0418 0.36 0.3470
#> [5,] -0.5 -0.1525 -0.3406 0.0355 0.25 0.2409
#> [6,] -0.4 -0.1083 -0.2487 0.0321 0.16 0.1542
#> [7,] -0.3 -0.0700 -0.1723 0.0323 0.09 0.0867
#> [8,] -0.2 -0.0354 -0.1097 0.0389 0.04 0.0386
#> [9,] -0.1 -0.0028 -0.0648 0.0591 0.01 0.0096
#> [10,] 0.0 0.0287 -0.0416 0.0990 0.00 0.0000
#> [11,] 0.1 0.0603 -0.0333 0.1538 0.01 0.0096
#> [12,] 0.2 0.0928 -0.0317 0.2173 0.04 0.0386
#> [13,] 0.3 0.1275 -0.0333 0.2882 0.09 0.0867
#> [14,] 0.4 0.1657 -0.0369 0.3684 0.16 0.1542
#> [15,] 0.5 0.2100 -0.0422 0.4621 0.25 0.2409
#> [16,] 0.6 0.2642 -0.0495 0.5779 0.36 0.3470
#> [17,] 0.7 0.3364 -0.0601 0.7329 0.49 0.4723
#> [18,] 0.8 0.4473 -0.0771 0.9717 0.64 0.6168
#> [19,] 0.9 0.6768 -0.1135 1.4672 0.81 0.7807
#>
#> Rho at which ACME = 0: -0.1
#> R^2_M*R^2_Y* at which ACME = 0: 0.01
#> R^2_M~R^2_Y~ at which ACME = 0: 0.0096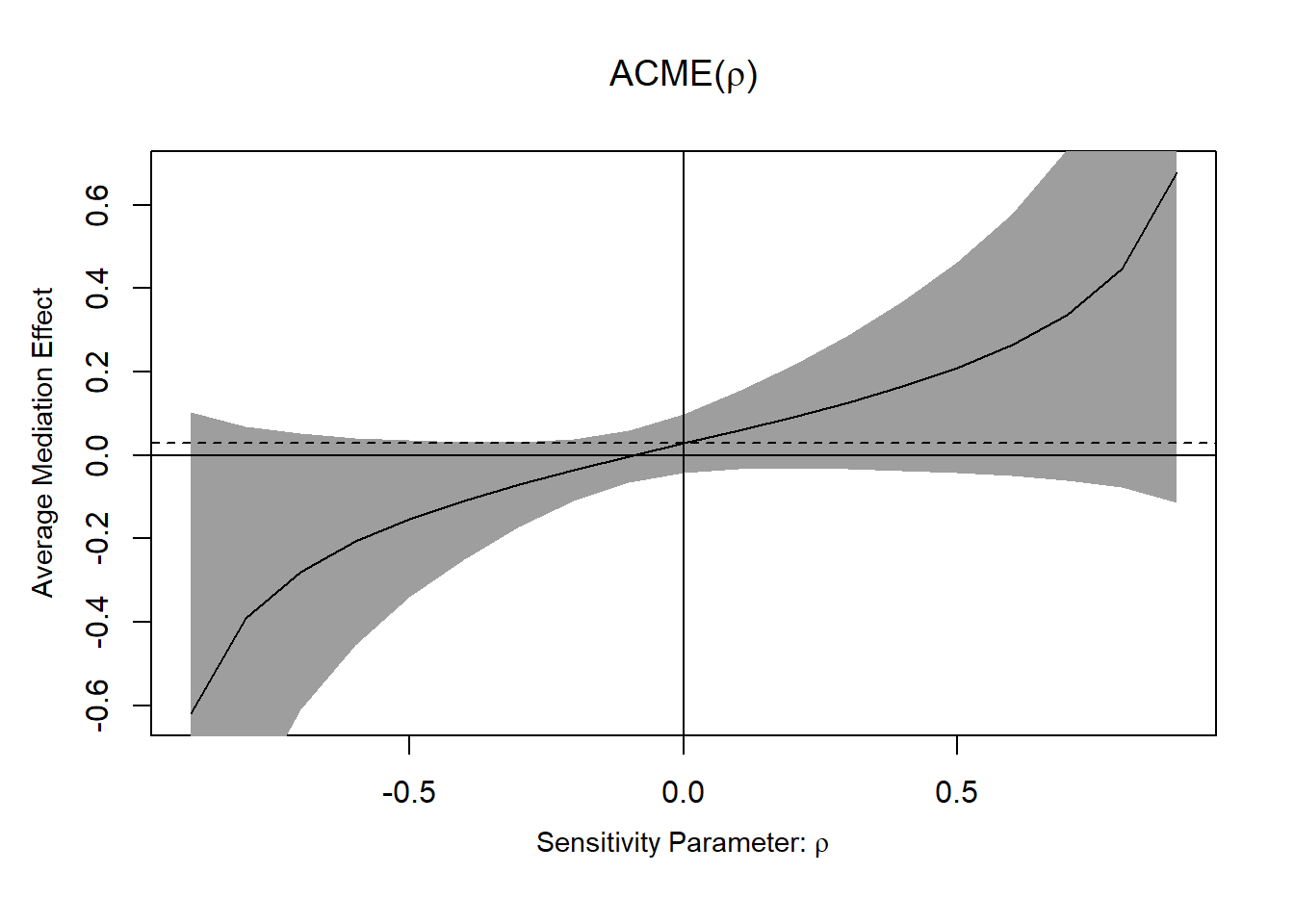
Figure 19.4: ACME
- If ACME confidence intervals contain 0, the effect is not robust to confounding.
Alternatively, using \(R^2\) interpretation, we need to specify the direction of confounder that affects the mediator and outcome variables in plot using sign.prod = "positive" (i.e., same direction) or sign.prod = "negative" (i.e., opposite direction).
| Aspect | Traditional Mediation | Causal Mediation |
|---|---|---|
| Model Assumption | Linear regressions | Potential outcomes framework |
| Assumptions Needed | No omitted confounders | Sequential ignorability |
| Inference Method | Product of coefficients | Counterfactual reasoning |
| Bootstrapping? | Common | Essential |
| Sensitivity Analysis? | Rarely used | Strongly recommended |