26.12 Assumptions
Parallel Trends: Difference between the treatment and control groups remain constant if there were no treatment.
should be used in cases where
you observe before and after an event
you have treatment and control groups
not in cases where
treatment is not random
confounders.
To support we use
Linear additive effects (of group/unit specific and time-specific):
If they are not additively interact, we have to use the weighted 2FE estimator (Imai and Kim 2021)
Typically seen in the Staggered Dif-n-dif
No anticipation: There is no causal effect of the treatment before its implementation.
Possible issues
Estimate dependent on functional form:
- When the size of the response depends (nonlinearly) on the size of the intervention, we might want to look at the the difference in the group with high intensity vs. low.
Selection on (time–varying) unobservables
- Can use the overall sensitivity of coefficient estimates to hidden bias using Rosenbaum Bounds
Long-term effects
- Parallel trends are more likely to be observed over shorter period (window of observation)
Heterogeneous effects
- Different intensity (e.g., doses) for different groups.
Ashenfelter dip (Ashenfelter and Card 1985) (job training program participant are more likely to experience an earning drop prior enrolling in these programs)
- Participants are systemically different from nonparticipants before the treatment, leading to the question of permanent or transitory changes.
- A fix to this transient endogeneity is to calculate long-run differences (exclude a number of periods symmetrically around the adoption/ implementation date). If we see a sustained impact, then we have strong evidence for the causal impact of a policy. (Proserpio and Zervas 2017b) (James J. Heckman and Smith 1999) (Jepsen, Troske, and Coomes 2014) (X. Li, Gan, and Hu 2011)
Response to event might not be immediate (can’t be observed right away in the dependent variable)
- Using lagged dependent variable \(Y_{it-1}\) might be more appropriate (Blundell and Bond 1998)
Other factors that affect the difference in trends between the two groups (i.e., treatment and control) will bias your estimation.
Correlated observations within a group or time
Incidental parameters problems (Lancaster 2000): it’s always better to use individual and time fixed effect.
When examining the effects of variation in treatment timing, we have to be careful because negative weights (per group) can be negative if there is a heterogeneity in the treatment effects over time. Example: [Athey and Imbens (2022)](Borusyak, Jaravel, and Spiess 2021)(Goodman-Bacon 2021). In this case you should use new estimands proposed by @callaway2021difference(Clément De Chaisemartin and d’Haultfoeuille 2020), in the
didpackage. If you expect lags and leads, see (L. Sun and Abraham 2021)(Gibbons, Suárez Serrato, and Urbancic 2018) caution when we suspect the treatment effect and treatment variance vary across groups
26.12.1 Prior Parallel Trends Test
- Plot the average outcomes over time for both treatment and control group before and after the treatment in time.
- Statistical test for difference in trends (using data from before the treatment period)
\[ Y = \alpha_g + \beta_1 T + \beta_2 T\times G + \epsilon \]
where
\(Y\) = the outcome variable
\(\alpha_g\) = group fixed effects
\(T\) = time (e.g., specific year, or month)
\(\beta_2\) = different time trends for each group
Hence, if \(\beta_2 =0\) provides evidence that there are no differences in the trend for the two groups prior the time treatment.
You can also use different functional forms (e..g, polynomial or nonlinear).
If \(\beta_2 \neq 0\) statistically, possible reasons can be:
Statistical significance can be driven by large sample
Or the trends are so consistent, and just one period deviation can throw off the trends. Hence, statistical statistical significance.
Technically, we can still salvage the research by including time fixed effects, instead of just the before-and-after time fixed effect (actually, most researchers do this mechanically anyway nowadays). However, a side effect can be that the time fixed effects can also absorb some part your treatment effect as well, especially in cases where the treatment effects vary with time (i.e., stronger or weaker over time) (Wolfers 2003).
Debate:
(Kahn-Lang and Lang 2020) argue that DiD will be more plausible when the treatment and control groups are similar not only in trends, but also in levels. Because when we observe dissimilar in levels prior to the treatment, why is it okay to think that this will not affect future trends?
Show a plot of the dependent variable’s time series for treated and control groups and also a similar plot with matched sample. (Ryan et al. 2019) show evidence of matched DiD did well in the setting of non-parallel trends (at least in health care setting).
In the case that we don’t have similar levels ex ante between treatment and control groups, functional form assumptions matter and we need justification for our choice.
Pre-trend statistical tests: (Roth 2022) provides evidence that these test are usually under powered.
- See PretrendsPower and pretrends packages for correcting this.
Parallel trends assumption is specific to both the transformation and units of the outcome (Roth and Sant’Anna 2023)
- See falsification test (\(H_0\): parallel trends is insensitive to functional form).
library(tidyverse)
library(fixest)
od <- causaldata::organ_donations %>%
# Use only pre-treatment data
filter(Quarter_Num <= 3) %>%
# Treatment variable
dplyr::mutate(California = State == 'California')
# use my package
causalverse::plot_par_trends(
data = od,
metrics_and_names = list("Rate" = "Rate"),
treatment_status_var = "California",
time_var = list(Quarter_Num = "Time"),
display_CI = F
)
#> [[1]]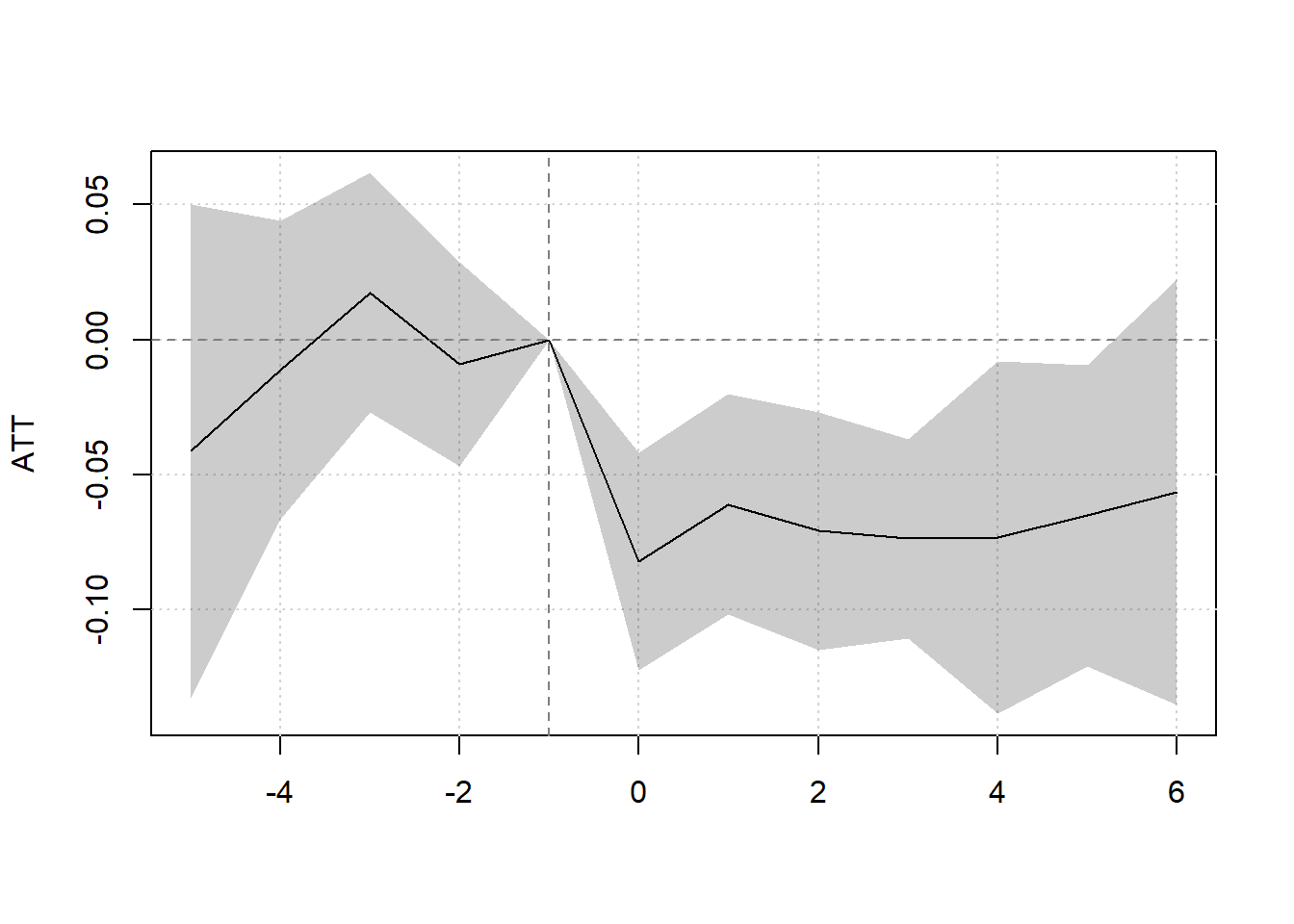
# do it manually
# always good but plot the dependent out
od |>
# group by treatment status and time
dplyr::group_by(California, Quarter) |>
dplyr::summarize_all(mean) |>
dplyr::ungroup() |>
# view()
ggplot2::ggplot(aes(x = Quarter_Num, y = Rate, color = California)) +
ggplot2::geom_line() +
causalverse::ama_theme()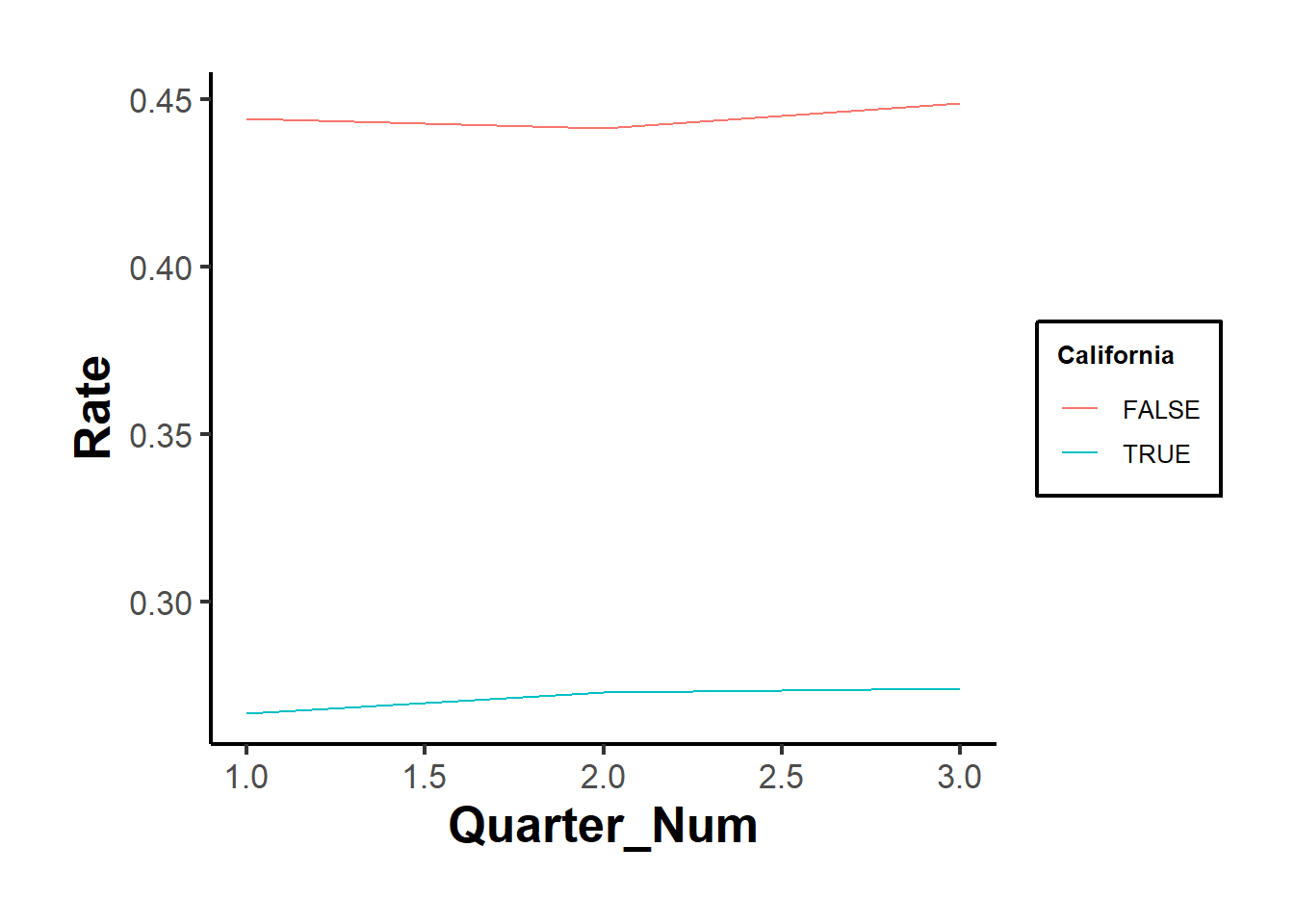
# but it's also important to use statistical test
prior_trend <- fixest::feols(Rate ~ i(Quarter_Num, California) | State + Quarter,
data = od)
fixest::coefplot(prior_trend, grid = F)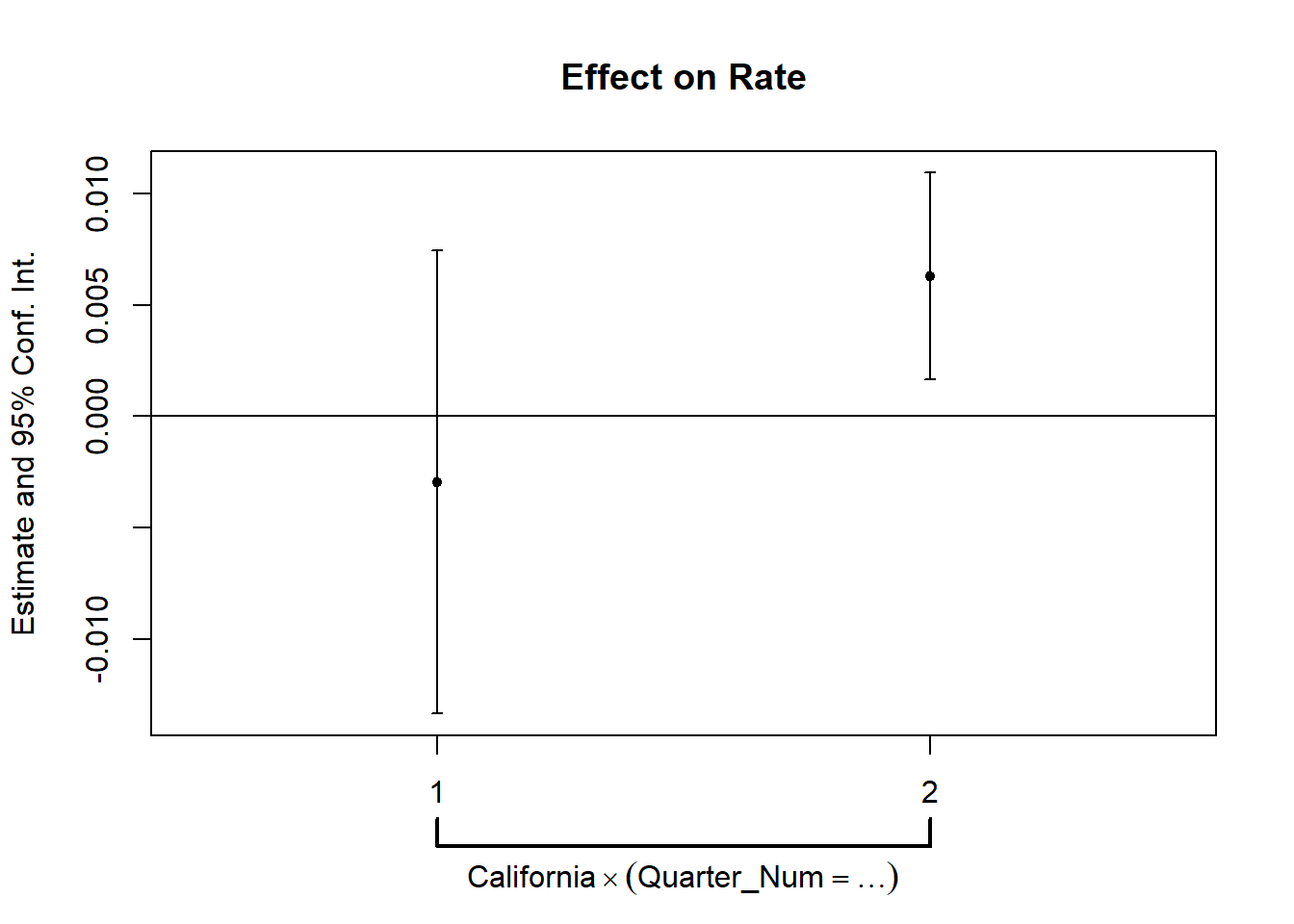
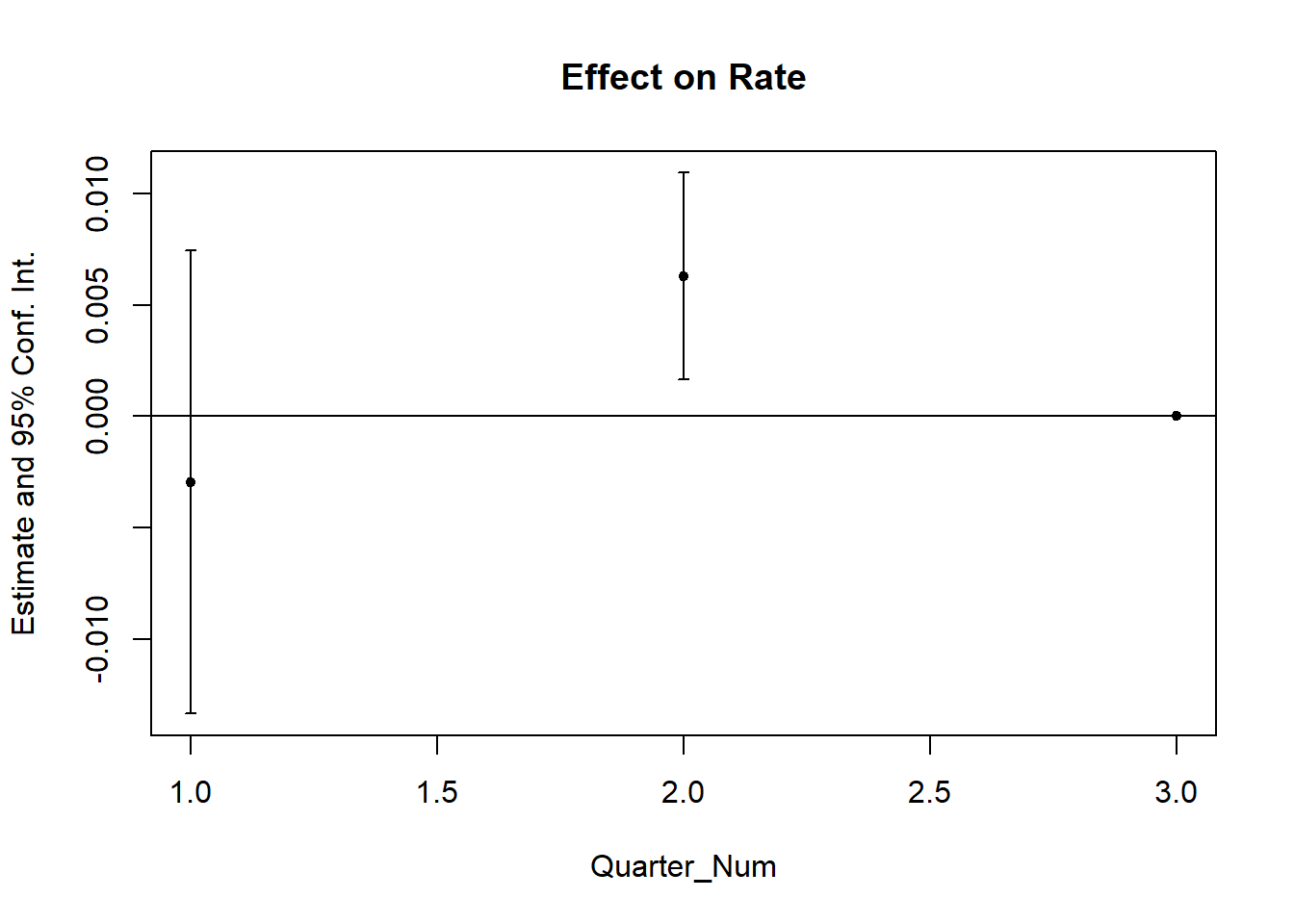
This is alarming since one of the periods is significantly different from 0, which means that our parallel trends assumption is not plausible.
In cases where you might have violations of parallel trends assumption, check (Rambachan and Roth 2023)
Impose restrictions on how different the post-treatment violations of parallel trends can be from the pre-trends.
Partial identification of causal parameter
Sensitivity analysis
# https://github.com/asheshrambachan/HonestDiD
# remotes::install_github("asheshrambachan/HonestDiD")
# library(HonestDiD)Alternatively, Ban and Kedagni (2022) propose a method that with an information set (i.e., pre-treatment covariates), and an assumption on the selection bias in the post-treatment period (i.e., lies within the convex hull of all selection biases), they can still identify a set of ATT, and with stricter assumption on selection bias from the policymakers perspective, they can also have a point estimate.
Alternatively, we can use the pretrends package to examine our assumptions (Roth 2022)
26.12.2 Placebo Test
Procedure:
- Sample data only in the period before the treatment in time.
- Consider different fake cutoff in time, either
Try the whole sequence in time
Generate random treatment period, and use randomization inference to account for sampling distribution of the fake effect.
- Estimate the DiD model but with the post-time = 1 with the fake cutoff
- A significant DiD coefficient means that you violate the parallel trends! You have a big problem.
Alternatively,
- When data have multiple control groups, drop the treated group, and assign another control group as a “fake” treated group. But even if it fails (i.e., you find a significant DiD effect) among the control groups, it can still be fine. However, this method is used under Synthetic Control
library(tidyverse)
library(fixest)
od <- causaldata::organ_donations %>%
# Use only pre-treatment data
dplyr::filter(Quarter_Num <= 3) %>%
# Create fake treatment variables
dplyr::mutate(
FakeTreat1 = State == 'California' &
Quarter %in% c('Q12011', 'Q22011'),
FakeTreat2 = State == 'California' &
Quarter == 'Q22011'
)
clfe1 <- fixest::feols(Rate ~ FakeTreat1 | State + Quarter,
data = od)
clfe2 <- fixest::feols(Rate ~ FakeTreat2 | State + Quarter,
data = od)
fixest::etable(clfe1,clfe2)
#> clfe1 clfe2
#> Dependent Var.: Rate Rate
#>
#> FakeTreat1TRUE 0.0061 (0.0051)
#> FakeTreat2TRUE -0.0017 (0.0028)
#> Fixed-Effects: --------------- ----------------
#> State Yes Yes
#> Quarter Yes Yes
#> _______________ _______________ ________________
#> S.E.: Clustered by: State by: State
#> Observations 81 81
#> R2 0.99377 0.99376
#> Within R2 0.00192 0.00015
#> ---
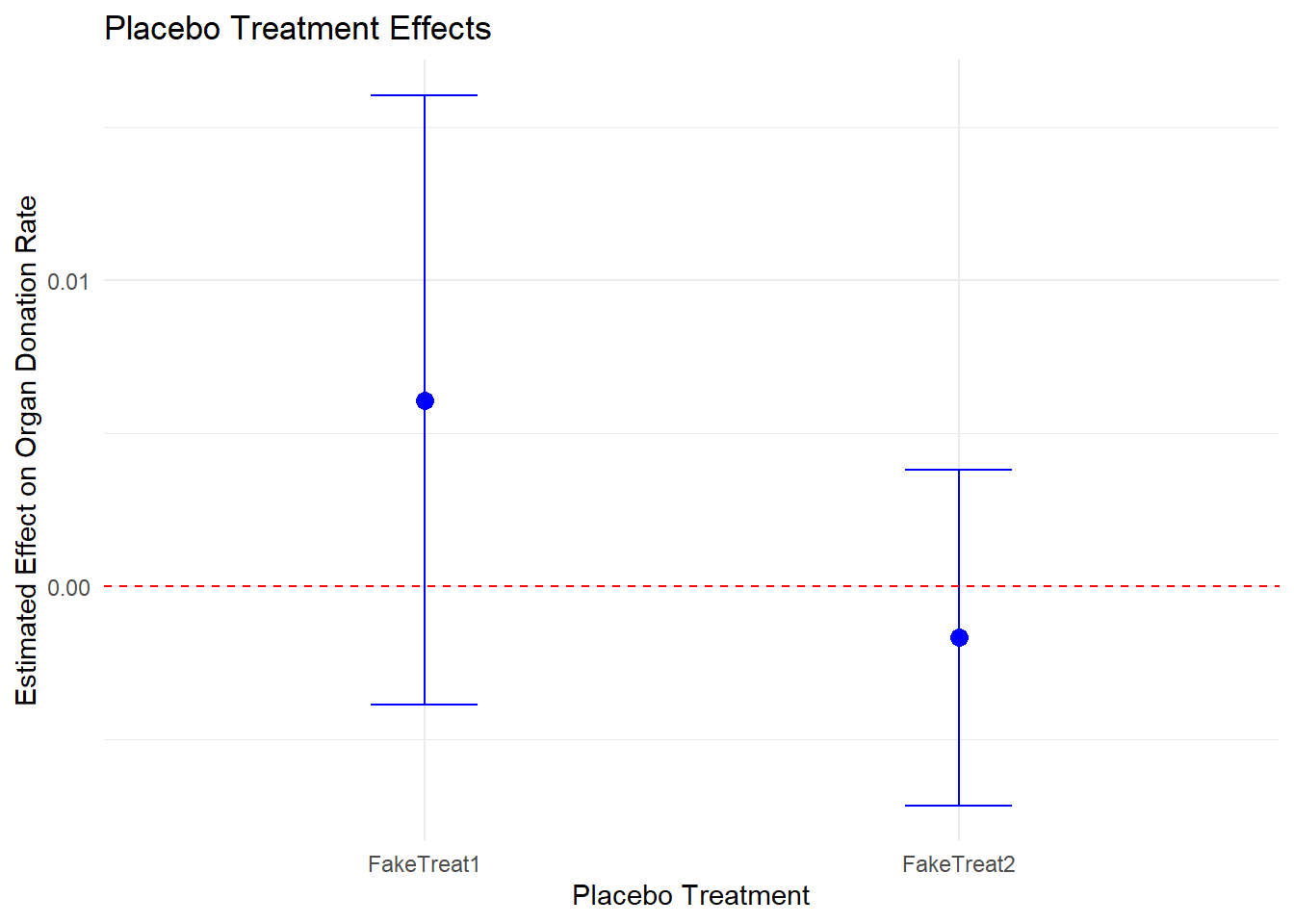
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1We would like the “supposed” DiD to be insignificant.
26.12.3 Assumption Violations
- Endogenous Timing
If the timing of units can be influenced by strategic decisions in a DID analysis, an instrumental variable approach with a control function can be used to control for endogeneity in timing.
- Questionable Counterfactuals
In situations where the control units may not serve as a reliable counterfactual for the treated units, matching methods such as propensity score matching or generalized random forest can be utilized. Additional methods can be found in Matching Methods.
26.12.4 Robustness Checks
Placebo DiD (if the DiD estimate \(\neq 0\), parallel trend is violated, and original DiD is biased):
Group: Use fake treatment groups: A population that was not affect by the treatment
Time: Redo the DiD analysis for period before the treatment (expected treatment effect is 0) (e.g., for previous year or period).
Possible alternative control group: Expected results should be similar
Try different windows (further away from the treatment point, other factors can creep in and nullify your effect).
Treatment Reversal (what if we don’t see the treatment event)
Higher-order polynomial time trend (to relax linearity assumption)
Test whether other dependent variables that should not be affected by the event are indeed unaffected.
- Use the same control and treatment period (DiD \(\neq0\), there is a problem)
The triple-difference strategy involves examining the interaction between the treatment variable and the probability of being affected by the program, and the group-level participation rate. The identification assumption is that there are no differential trends between high and low participation groups in early versus late implementing countries.