39.3 Neutral Controls

39.3.1 Good Predictive Controls

Good for precision

# cleans workspace
rm(list = ls())

# DAG

## specify edges
model <- dagitty("dag{x->y; z->y}")


## coordinates for plotting
coordinates(model) <-  list(
  x = c(x=1, z=2, y=2),
  y = c(x=1, z=2, y=1))

## ggplot
ggdag(model) + theme_dag()

Controlling for \(Z\) does not help or hurt identification, but it can increase precision (i.e., reducing SE)

n <- 1e4
z <- rnorm(n)
x <- rnorm(n)
y <- x + 2 * z + rnorm(n)

jtools::export_summs(lm(y ~ x), lm(y ~ x + z))

Table 38.13:

	Model 1	Model 2
(Intercept)	0.01	0.01
	(0.02)	(0.01)
x	1.00 ***	1.01 ***
	(0.02)	(0.01)
z		2.00 ***
		(0.01)
N	10000	10000
R2	0.17	0.83
*** p < 0.001; ** p < 0.01; * p < 0.05.

Similar coefficients, but smaller SE when controlling for \(Z\)

Another variation is

# cleans workspace
rm(list = ls())

# DAG

## specify edges
model <- dagitty("dag{x->y; x->m; z->m; m->y}")

## coordinates for plotting
coordinates(model) <-  list(
  x = c(x=1, z=2, m=2, y=3),
  y = c(x=1, z=2, m=1, y=1))

## ggplot
ggdag(model) + theme_dag()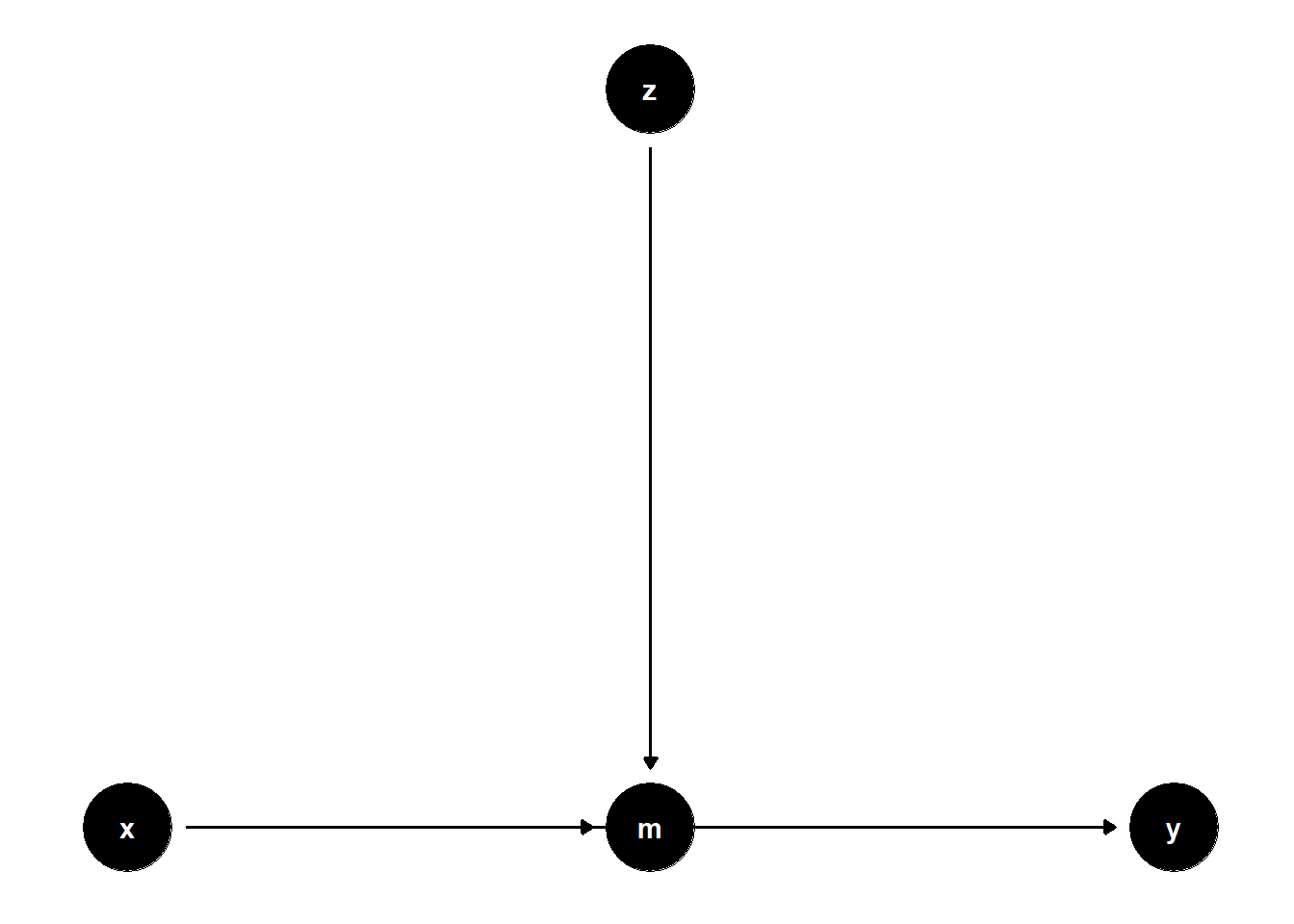

n <- 1e4
z <- rnorm(n)
x <- rnorm(n)
m <- 2 * z + rnorm(n)
y <- x + 2 * m + rnorm(n)

jtools::export_summs(lm(y ~ x), lm(y ~ x + z))

Table 38.14:

	Model 1	Model 2
(Intercept)	-0.00	-0.00
	(0.05)	(0.02)
x	0.97 ***	0.99 ***
	(0.05)	(0.02)
z		4.02 ***
		(0.02)
N	10000	10000
R2	0.04	0.77
*** p < 0.001; ** p < 0.01; * p < 0.05.

Controlling for \(Z\) can reduce SE

39.3.2 Good Selection Bias

# cleans workspace
rm(list = ls())

# DAG

## specify edges
model <- dagitty("dag{x->y; x->z; z->w; u->w;u->y}")

# set u as latent
latents(model) <- "u"

## coordinates for plotting
coordinates(model) <-  list(
  x = c(x=1, z=2, w=3, u=3, y=5),
  y = c(x=3, z=2, w=1, u=4, y=3))

## ggplot
ggdag(model) + theme_dag()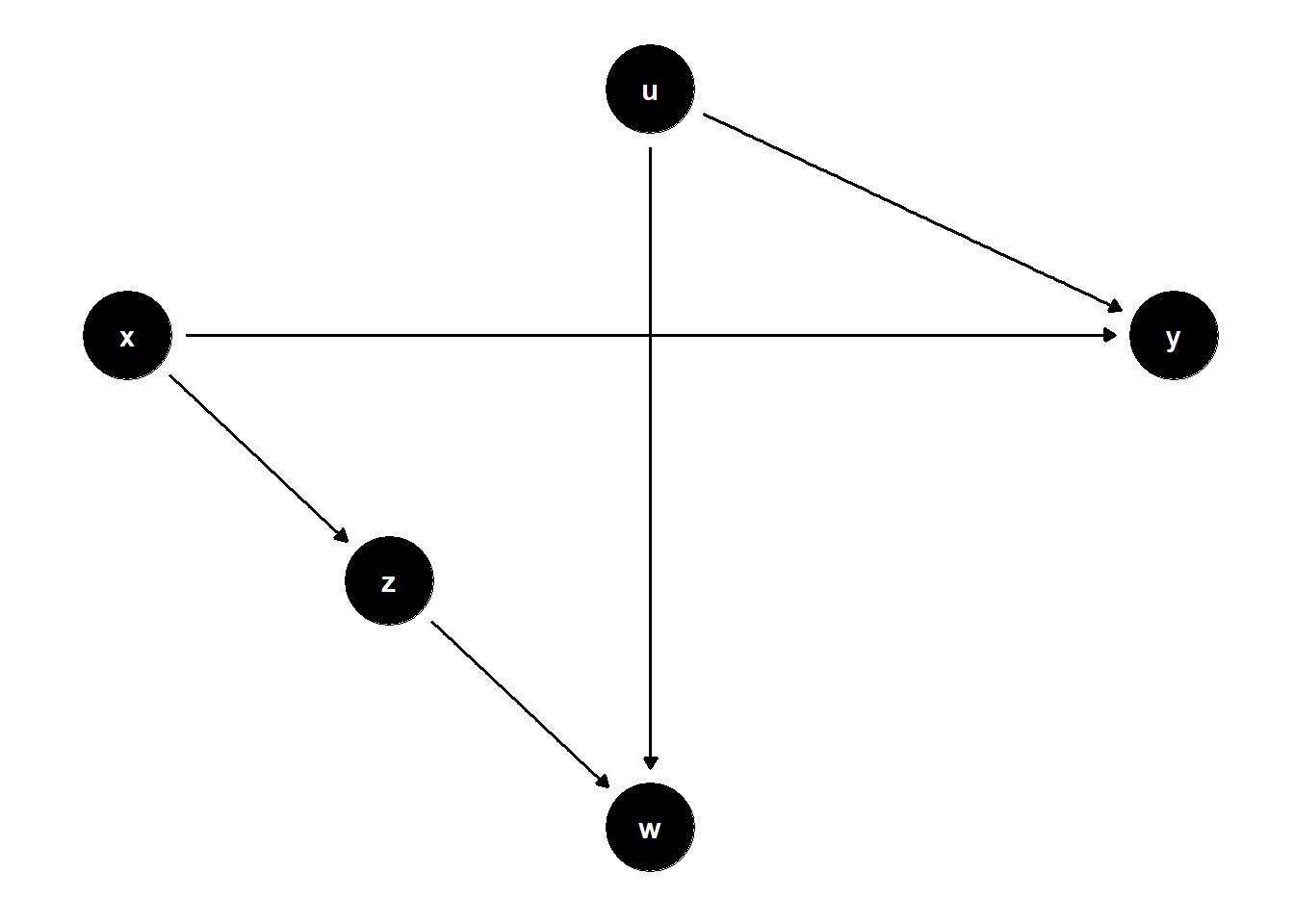

1. Unadjusted estimate is unbiased
2. Controlling for Z can increase SE
3. Controlling for Z while having on W can help identify X

n <- 1e4
x <- rnorm(n)
u <- rnorm(n)
z <- x + rnorm(n)
w <- z + u + rnorm(n)
y <- x - 2*u + rnorm(n)

jtools::export_summs(lm(y ~ x), lm(y ~ x + w), lm(y ~ x + z + w))

Table 38.15:

	Model 1	Model 2	Model 3
(Intercept)	0.01	0.01	0.03
	(0.02)	(0.02)	(0.02)
x	0.99 ***	1.65 ***	0.99 ***
	(0.02)	(0.02)	(0.02)
w		-0.67 ***	-1.01 ***
		(0.01)	(0.01)
z			1.02 ***
			(0.02)
N	10000	10000	10000
R2	0.16	0.39	0.50
*** p < 0.001; ** p < 0.01; * p < 0.05.

39.3.3 Bad Predictive Controls

# cleans workspace
rm(list = ls())

# DAG

## specify edges
model <- dagitty("dag{x->y; z->x}")


## coordinates for plotting
coordinates(model) <-  list(
  x = c(x=1, z=1, y=2),
  y = c(x=1, z=2, y=1))

## ggplot
ggdag(model) + theme_dag()

n <- 1e4
z <- rnorm(n)
x <- 2 * z + rnorm(n)
y <- x + 2 * rnorm(n)

jtools::export_summs(lm(y ~ x), lm(y ~ x + z))

Table 38.16:

	Model 1	Model 2
(Intercept)	-0.02	-0.02
	(0.02)	(0.02)
x	0.99 ***	1.00 ***
	(0.01)	(0.02)
z		-0.00
		(0.04)
N	10000	10000
R2	0.55	0.55
*** p < 0.001; ** p < 0.01; * p < 0.05.

Similar coefficients, but greater SE when controlling for \(Z\)

Another variation is

rm(list = ls())

# DAG

## specify edges
model <- dagitty("dag{x->y; x->z}")


## coordinates for plotting
coordinates(model) <-  list(
  x = c(x=1, z=1, y=2),
  y = c(x=1, z=2, y=1))

## ggplot
ggdag(model) + theme_dag()

set.seed(1)
n <- 1e4
x <- rnorm(n)
z <- 2 * x + rnorm(n)
y <- x + 2 * rnorm(n)

jtools::export_summs(lm(y ~ x), lm(y ~ x + z))

Table 38.17:

	Model 1	Model 2
(Intercept)	0.02	0.02
	(0.02)	(0.02)
x	1.00 ***	0.99 ***
	(0.02)	(0.05)
z		0.00
		(0.02)
N	10000	10000
R2	0.20	0.20
*** p < 0.001; ** p < 0.01; * p < 0.05.

Worse SE when controlling for \(Z\) (\(0.02 < 0.05\))

39.3.4 Bad Selection Bias

# cleans workspace
rm(list = ls())

# DAG

## specify edges
model <- dagitty("dag{x->y; x->z}")


## coordinates for plotting
coordinates(model) <-  list(
  x = c(x=1, z=2, y=2),
  y = c(x=1, z=2, y=1))

## ggplot
ggdag(model) + theme_dag()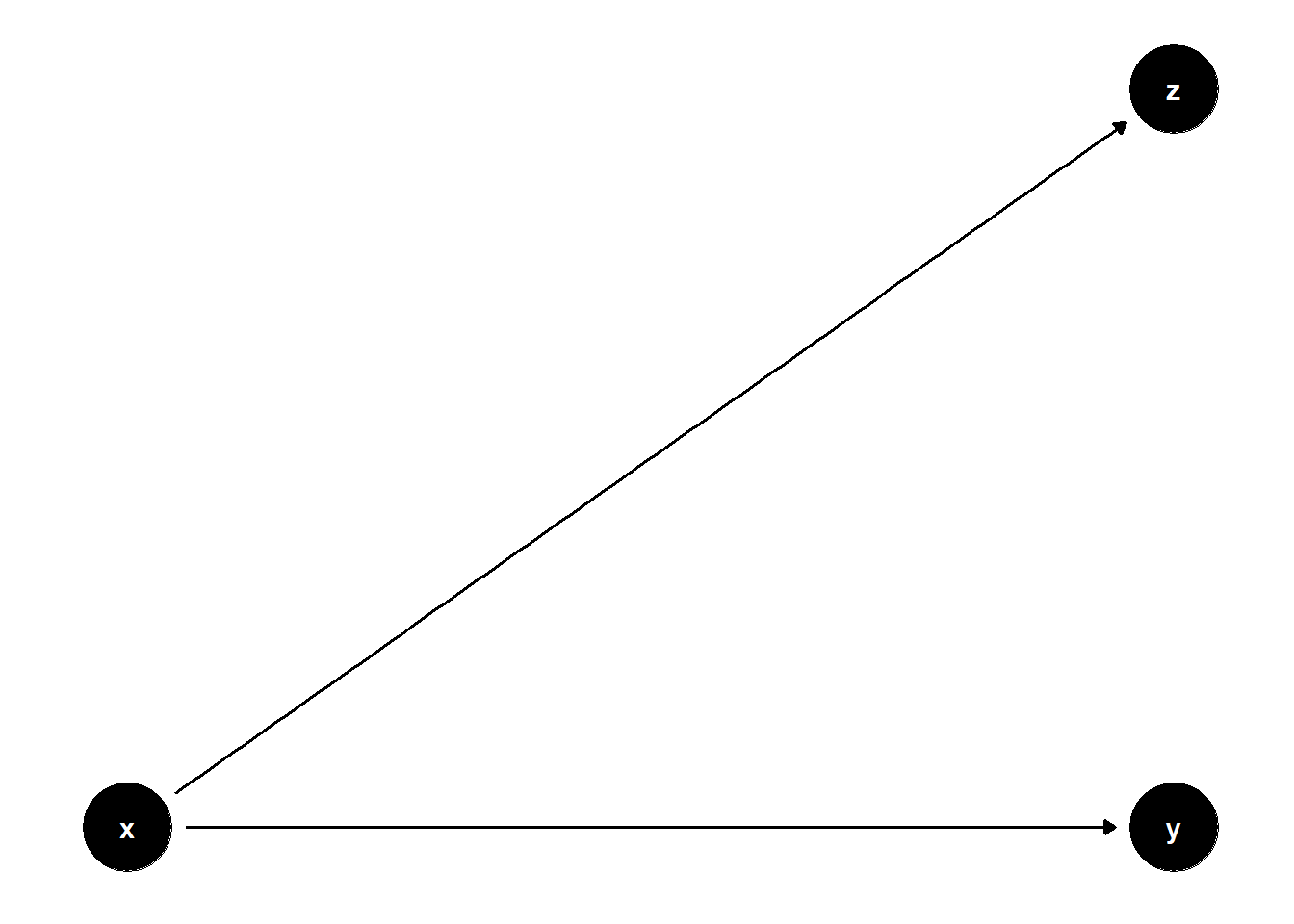

Not all post-treatment variables are bad.

Controlling for \(Z\) is neutral, but it might hurt the precision of the causal effect.