15 Marginal Effects
In cases without polynomials or interactions, it can be easy to interpret the marginal effect.
For example,
\[ Y = \beta_1 X_1 + \beta_2 X_2 \]
where \(\beta\) are the marginal effects.
Numerical derivation is easier than analytical derivation.
- We need to choose values for all the variables to calculate the marginal effect of \(X\)
Analytical derivation
\[ f'(x) \equiv \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} \]
E.g., \(f(x) = X^2\)
\[ \begin{aligned} f'(x) &= \lim_{h \to 0} \frac{(x+h)^2 - x^2}{h} \\ &= \frac{x^2 + 2xh + h^2 - x^2}{h} \\ &= \frac{2xh + h^2}{h} \\ &= 2x + h \\ &= 2x \end{aligned} \]
For numerically approach, we “just” need to find a small \(h\) to plug in our function. However, you also need a large enough \(h\) to have numerically accurate computation (Gould, Pitblado, and Poi 2010, chap. 1)
Numerically approach
One-sided derivative
\[ \begin{aligned} f'(x) &= \lim_{h \to 0} \frac{(x+h)^2 - x^2}{h} \\ & \approx \frac{f(x+h) -f(x)}{h} \end{aligned} \]
Alternatively, two-sided derivative
\[ f'_2(x) \approx \frac{f(x+h) - f(x- h)}{2h} \]
Marginal effects for
discrete variables (also known as incremental effects) are the change in \(E[Y|X]\) for a one unit change in \(X\)
continuous variables are the change in \(E[Y|X]\) for very small changes in \(X\) (not unit changes), because it’s a derivative, which is a limit when \(h \to 0\)
| Analytical derivation | Numerical derivation | |
|---|---|---|
| Marginal Effects | Rules of expectations | Approximate analytical solution |
| Standard Errors | Rules of variances | Delta method using the asymptotic errors (vcov matrix) |
15.1 Delta Method
- approximate the mean and variance of a function of random variables using a first-order Taylor approximation
- A semi-parametric method
- Alternative approaches:
Analytically derive a probability function for the margin
Simulation/Bootstrapping
- Resources:
Advanced: modmarg
Intermediate: UCLA stat
Simple: Another one
Let \(G(\beta)\) be a function of the parameters \(\beta\), then
\[ var(G(\beta)) \approx \nabla G(\beta) cov (\beta) \nabla G(\beta)' \]
where
- \(\nabla G(\beta)\) = the gradient of the partial derivatives of \(G(\beta)\) (also known as the Jacobian)
15.2 Average Marginal Effect Algorithm
For one-sided derivative \(\frac{\partial p(\mathbf{X},\beta)}{\partial X}\) in the probability scale
- Estimate your model
- For each observation \(i\)
Calculate \(\hat{Y}_{i0}\) which is the prediction in the probability scale using observed values
-
Increase \(X\) (variable of interest) by a “small” amount \(h\) (\(X_{new} = X + h\))
When \(X\) is continuous, \(h = (|\bar{X}| + 0.001) \times 0.001\) where \(\bar{X}\) is the mean value of \(X\)
When \(X\) is discrete, \(h = 1\)
Calculate \(\hat{Y}_{i1}\) which is the prediction in the probability scale using new \(X\) and other variables’ observed vales.
Calculate the difference between the two predictions as fraction of \(h\): \(\frac{\bar{Y}_{i1} - \bar{Y}_{i0}}{h}\)
- Average numerical derivative is \(E[\frac{\bar{Y}_{i1} - \bar{Y}_{i0}}{h}] \approx \frac{\partial p (Y|\mathbf{X}, \beta)}{\partial X}\)
Two-sided derivatives
- Estimate your model
- For each observation \(i\)
Calculate \(\hat{Y}_{i0}\) which is the prediction in the probability scale using observed values
-
Increase \(X\) (variable of interest) by a “small” amount \(h\) (\(X_{1} = X + h\)) and decrease \(X\) (variable of interest) by a “small” amount \(h\) (\(X_{2} = X - h\))
When \(X\) is continuous, \(h = (|\bar{X}| + 0.001) \times 0.001\) where \(\bar{X}\) is the mean value of \(X\)
When \(X\) is discrete, \(h = 1\)
Calculate \(\hat{Y}_{i1}\) which is the prediction in the probability scale using new \(X_1\) and other variables’ observed vales.
Calculate \(\hat{Y}_{i2}\) which is the prediction in the probability scale using new \(X_2\) and other variables’ observed vales.
Calculate the difference between the two predictions as fraction of \(h\): \(\frac{\bar{Y}_{i1} - \bar{Y}_{i2}}{2h}\)
- Average numerical derivative is \(E[\frac{\bar{Y}_{i1} - \bar{Y}_{i2}}{2h}] \approx \frac{\partial p (Y|\mathbf{X}, \beta)}{\partial X}\)
library(margins)
library(tidyverse)
data("mtcars")
mod <- lm(mpg ~ cyl * disp * hp, data = mtcars)
margins::margins(mod) %>% summary()
#> factor AME SE z p lower upper
#> cyl -4.0592 3.7614 -1.0792 0.2805 -11.4313 3.3130
#> disp -0.0350 0.0132 -2.6473 0.0081 -0.0610 -0.0091
#> hp -0.0284 0.0185 -1.5348 0.1248 -0.0647 0.0079
# function for variable
get_mae <- function(mod, var = "disp") {
data = mod$model
pred <- predict(mod)
if (class(mod$model[[{
{
var
}
}]]) == "numeric") {
h = (abs(mean(mod$model[[var]])) + 0.01) * 0.01
} else {
h = 1
}
data[[{
{
var
}
}]] <- data[[{
{
var
}
}]] - h
pred_new <- predict(mod, newdata = data)
mean(pred - pred_new) / h
}
get_mae(mod, var = "disp")
#> [1] -0.0350454615.3 Packages
15.3.1 MarginalEffects
MarginalEffects package is a successor of margins and emtrends (faster, more efficient, more adaptable). Hence, this is advocated to be used.
- A limitation is that there is no readily function to correct for multiple comparisons. Hence, one can use the
p.adjustfunction to overcome this disadvantage.
Definitions from the package:
-
Marginal effects are slopes or derivatives (i.e., effect of changes in a variable on the outcome)
-
marginspackage defines marginal effects as “partial derivatives of the regression equation with respect to each variable in the model for each unit in the data.”
-
Marginal means are averages or integrals (i.e., marginalizing across rows of a prediction grid)
To customize your plot using plot_cme (which is a ggplot class), you can check this post by the author of the MarginalEffects package
Causal inference with the parametric g-formula
- Because the plug-in g estimator is equivalent to the average contrast in the
marginaleffectspackage.
To get predicted values
library(marginaleffects)
library(tidyverse)
data(mtcars)
mod <- lm(mpg ~ hp * wt * am, data = mtcars)
predictions(mod) %>% head()
#>
#> Estimate Std. Error z Pr(>|z|) S 2.5 % 97.5 %
#> 22.5 0.884 25.4 <0.001 471.7 20.8 24.2
#> 20.8 1.194 17.4 <0.001 223.3 18.5 23.1
#> 25.3 0.709 35.7 <0.001 922.7 23.9 26.7
#> 20.3 0.704 28.8 <0.001 601.5 18.9 21.6
#> 17.0 0.712 23.9 <0.001 416.2 15.6 18.4
#> 19.7 0.875 22.5 <0.001 368.8 17.9 21.4
#>
#> Columns: rowid, estimate, std.error, statistic, p.value, s.value, conf.low, conf.high, mpg, hp, wt, am
# for specific reference values
predictions(mod, newdata = datagrid(am = 0, wt = c(2, 4)))
#>
#> am wt Estimate Std. Error z Pr(>|z|) S 2.5 % 97.5 % hp
#> 0 2 22.0 2.04 10.8 <0.001 87.4 18.0 26.0 147
#> 0 4 16.6 1.08 15.3 <0.001 173.8 14.5 18.7 147
#>
#> Columns: rowid, estimate, std.error, statistic, p.value, s.value, conf.low, conf.high, mpg, hp, am, wt
plot_cap(mod, condition = c("hp","wt"))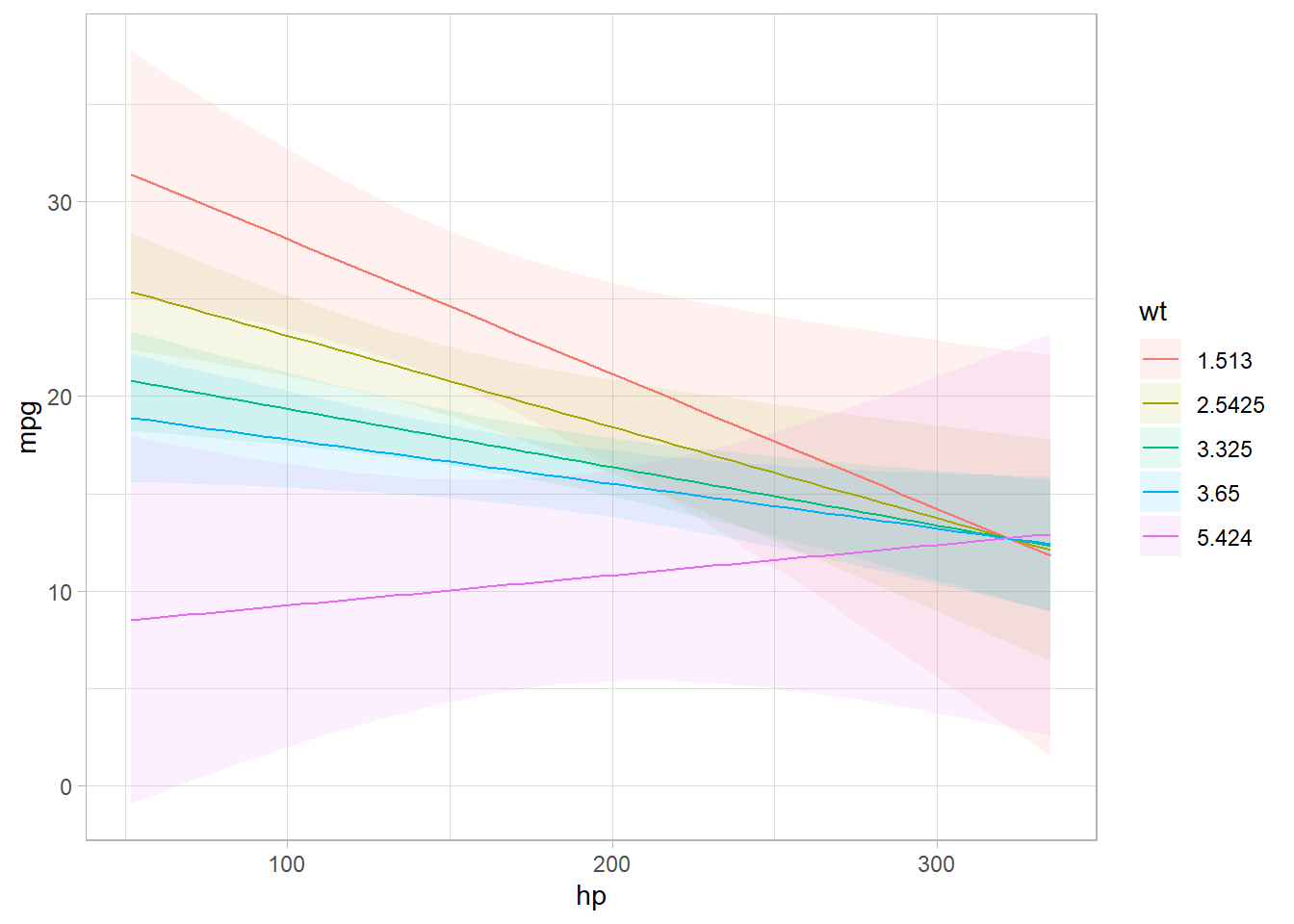
# Average Margianl Effects
mfx <- marginaleffects(mod, variables = c("hp", "wt"))
summary(mfx)
#>
#> Term Contrast Estimate Std. Error z Pr(>|z|) 2.5 % 97.5 %
#> hp mean(dY/dX) -0.0381 0.0128 -2.98 0.00291 -0.0631 -0.013
#> wt mean(dY/dX) -3.9391 1.0858 -3.63 < 0.001 -6.0672 -1.811
#>
#> Columns: term, contrast, estimate, std.error, statistic, p.value, conf.low, conf.high
# Group-Average Marginal Effects
marginaleffects::marginaleffects(mod, by = "hp", variables = "am")
#>
#> Term Contrast hp Estimate Std. Error z Pr(>|z|) S 2.5 %
#> am mean(1) - mean(0) 52 3.976 5.20 0.764 0.445 1.2 -6.22
#> am mean(1) - mean(0) 62 -2.774 2.51 -1.107 0.268 1.9 -7.68
#> am mean(1) - mean(0) 65 2.999 4.13 0.725 0.468 1.1 -5.10
#> am mean(1) - mean(0) 66 2.025 3.48 0.582 0.561 0.8 -4.80
#> am mean(1) - mean(0) 91 1.858 2.76 0.674 0.500 1.0 -3.54
#> am mean(1) - mean(0) 93 1.201 2.35 0.511 0.609 0.7 -3.40
#> am mean(1) - mean(0) 95 -1.832 1.97 -0.931 0.352 1.5 -5.69
#> am mean(1) - mean(0) 97 0.708 2.04 0.347 0.728 0.5 -3.28
#> am mean(1) - mean(0) 105 -2.682 2.37 -1.132 0.258 2.0 -7.32
#> am mean(1) - mean(0) 109 -0.237 1.59 -0.149 0.881 0.2 -3.35
#> am mean(1) - mean(0) 110 -0.640 1.57 -0.407 0.684 0.5 -3.73
#> am mean(1) - mean(0) 113 4.081 3.94 1.037 0.300 1.7 -3.63
#> am mean(1) - mean(0) 123 -2.098 2.10 -0.998 0.318 1.7 -6.22
#> am mean(1) - mean(0) 150 -1.429 1.90 -0.753 0.452 1.1 -5.15
#> am mean(1) - mean(0) 175 -0.416 1.56 -0.266 0.790 0.3 -3.48
#> am mean(1) - mean(0) 180 -1.381 2.47 -0.560 0.576 0.8 -6.22
#> am mean(1) - mean(0) 205 -2.873 6.24 -0.460 0.645 0.6 -15.11
#> am mean(1) - mean(0) 215 -2.534 6.95 -0.364 0.716 0.5 -16.16
#> am mean(1) - mean(0) 230 -1.477 7.07 -0.209 0.835 0.3 -15.34
#> am mean(1) - mean(0) 245 1.115 2.28 0.488 0.625 0.7 -3.36
#> am mean(1) - mean(0) 264 2.106 2.29 0.920 0.358 1.5 -2.38
#> am mean(1) - mean(0) 335 4.027 3.24 1.243 0.214 2.2 -2.32
#> 97.5 %
#> 14.18
#> 2.14
#> 11.10
#> 8.85
#> 7.26
#> 5.80
#> 2.02
#> 4.70
#> 1.96
#> 2.87
#> 2.45
#> 11.79
#> 2.02
#> 2.29
#> 2.64
#> 3.46
#> 9.36
#> 11.09
#> 12.39
#> 5.59
#> 6.59
#> 10.38
#>
#> Columns: term, contrast, hp, estimate, std.error, statistic, p.value, s.value, conf.low, conf.high, predicted_lo, predicted_hi, predicted
# Marginal effects at representative values
marginaleffects::marginaleffects(mod,
newdata = datagrid(am = 0,
wt = c(2, 4)))
#>
#> Term Contrast am wt Estimate Std. Error z Pr(>|z|) S 2.5 % 97.5 %
#> am 1 - 0 0 2 2.5465 2.7860 0.914 0.3607 1.5 -2.9139 8.00694
#> am 1 - 0 0 4 -2.9661 3.0381 -0.976 0.3289 1.6 -8.9207 2.98852
#> hp dY/dX 0 2 -0.0598 0.0283 -2.115 0.0344 4.9 -0.1153 -0.00439
#> hp dY/dX 0 4 -0.0309 0.0187 -1.654 0.0981 3.3 -0.0676 0.00572
#> wt dY/dX 0 2 -2.6762 1.4194 -1.885 0.0594 4.1 -5.4582 0.10587
#> wt dY/dX 0 4 -2.6762 1.4199 -1.885 0.0595 4.1 -5.4591 0.10676
#>
#> Columns: rowid, term, contrast, estimate, std.error, statistic, p.value, s.value, conf.low, conf.high, am, wt, predicted_lo, predicted_hi, predicted, mpg, hp
# Marginal Effects at the Mean
marginaleffects::marginaleffects(mod, newdata = "mean")
#>
#> Term Contrast Estimate Std. Error z Pr(>|z|) S 2.5 % 97.5 %
#> am 1 - 0 -0.8086 1.52383 -0.531 0.59568 0.7 -3.795 2.1781
#> hp dY/dX -0.0323 0.00956 -3.375 < 0.001 10.4 -0.051 -0.0135
#> wt dY/dX -3.7959 1.21310 -3.129 0.00175 9.2 -6.174 -1.4183
#>
#> Columns: rowid, term, contrast, estimate, std.error, statistic, p.value, s.value, conf.low, conf.high, predicted_lo, predicted_hi, predicted, mpg, hp, wt, am
# counterfactual
comparisons(mod, variables = list(am = 0:1)) %>% summary()
#>
#> Term Contrast Estimate Std. Error z Pr(>|z|) 2.5 % 97.5 %
#> am mean(1) - mean(0) -0.0481 1.85 -0.026 0.979 -3.68 3.58
#>
#> Columns: term, contrast, estimate, std.error, statistic, p.value, conf.low, conf.high15.3.2 margins
- Marginal effects are partial derivative of the regression equation with respect to each variable in the model for each unit in the data
Average Partial Effects: the contribution of each variable the outcome scale, conditional on the other variables involved in the link function transformation of the linear predictor
Average Marginal Effects: the marginal contribution of each variable on the scale of the linear predictor.
Average marginal effects are the mean of these unit-specific partial derivatives over some sample
margins package gives the marginal effects of models (a replication of the margins command in Stata).
prediction package gives the unit-specific and sample average predictions of models (similar to the predictive margins in Stata).
library(margins)
# examples by the package's authors
mod <- lm(mpg ~ cyl * hp + wt, data = mtcars)
summary(mod)
#>
#> Call:
#> lm(formula = mpg ~ cyl * hp + wt, data = mtcars)
#>
#> Residuals:
#> Min 1Q Median 3Q Max
#> -3.3440 -1.4144 -0.6166 1.2160 4.2815
#>
#> Coefficients:
#> Estimate Std. Error t value Pr(>|t|)
#> (Intercept) 52.017520 4.916935 10.579 4.18e-11 ***
#> cyl -2.742125 0.800228 -3.427 0.00197 **
#> hp -0.163594 0.052122 -3.139 0.00408 **
#> wt -3.119815 0.661322 -4.718 6.51e-05 ***
#> cyl:hp 0.018954 0.006645 2.852 0.00823 **
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 2.242 on 27 degrees of freedom
#> Multiple R-squared: 0.8795, Adjusted R-squared: 0.8616
#> F-statistic: 49.25 on 4 and 27 DF, p-value: 5.065e-12In cases where you have interaction or polynomial terms, the coefficient estimates cannot be interpreted as the marginal effects of X on Y. Hence, if you want to know the average marginal effects of each variable then
summary(margins(mod))
#> factor AME SE z p lower upper
#> cyl 0.0381 0.5999 0.0636 0.9493 -1.1376 1.2139
#> hp -0.0463 0.0145 -3.1909 0.0014 -0.0748 -0.0179
#> wt -3.1198 0.6613 -4.7176 0.0000 -4.4160 -1.8236
# equivalently
margins_summary(mod)
#> factor AME SE z p lower upper
#> cyl 0.0381 0.5999 0.0636 0.9493 -1.1376 1.2139
#> hp -0.0463 0.0145 -3.1909 0.0014 -0.0748 -0.0179
#> wt -3.1198 0.6613 -4.7176 0.0000 -4.4160 -1.8236
plot(margins(mod))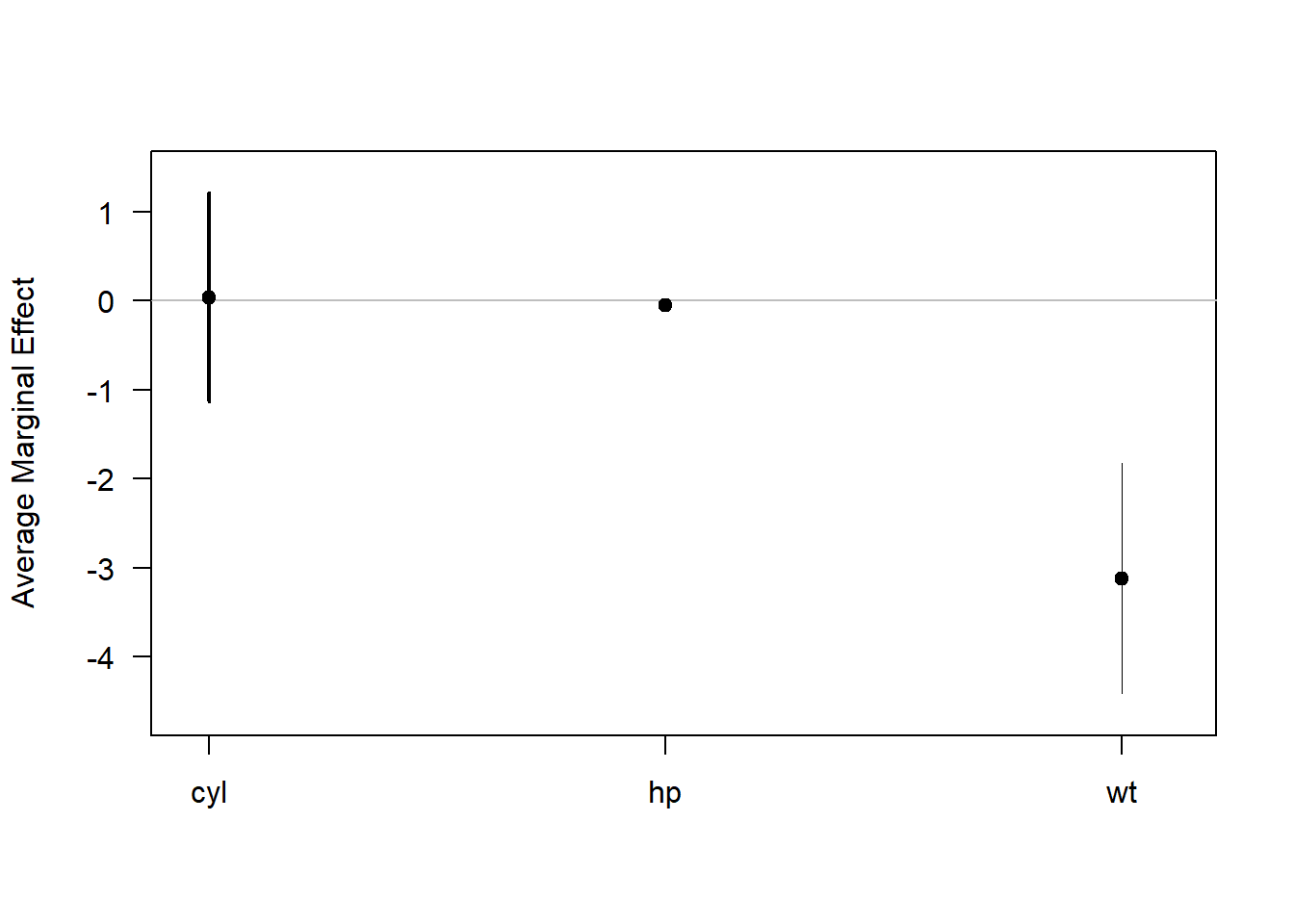
Marginal effects at the mean (MEM):
- Marginal effects at the mean values of the sample
- For discrete variables, it’s called average discrete change (ADC)
Average Marginal Effect (AME)
- An average of the marginal effects at each value of the sample
Marginal Effects at representative values (MER)
margins(mod, at = list(hp = 150))
#> at(hp) cyl hp wt
#> 150 0.1009 -0.04632 -3.12
margins(mod, at = list(hp = 150)) %>% summary()
#> factor hp AME SE z p lower upper
#> cyl 150.0000 0.1009 0.6128 0.1647 0.8692 -1.1001 1.3019
#> hp 150.0000 -0.0463 0.0145 -3.1909 0.0014 -0.0748 -0.0179
#> wt 150.0000 -3.1198 0.6613 -4.7175 0.0000 -4.4160 -1.823615.3.3 mfx
Works well with Generalized Linear Models/glm package
For technical details, see the package vignette
| Model | Dependent Variable | Syntax |
|---|---|---|
| Probit | Binary | probitmfx |
| Logit | Binary | logitmfx |
| Poisson | Count | poissonmfx |
| Negative Binomial | Count | negbinmfx |
| Beta | Rate | betamfx |
library(mfx)
data("mtcars")
poissonmfx(formula = vs ~ mpg * cyl * disp, data = mtcars)
#> Call:
#> poissonmfx(formula = vs ~ mpg * cyl * disp, data = mtcars)
#>
#> Marginal Effects:
#> dF/dx Std. Err. z P>|z|
#> mpg 1.4722e-03 8.7531e-03 0.1682 0.8664
#> cyl 6.6420e-03 3.9263e-02 0.1692 0.8657
#> disp 1.5899e-04 9.4555e-04 0.1681 0.8665
#> mpg:cyl -3.4698e-04 2.0564e-03 -0.1687 0.8660
#> mpg:disp -7.6794e-06 4.5545e-05 -0.1686 0.8661
#> cyl:disp -3.3837e-05 1.9919e-04 -0.1699 0.8651
#> mpg:cyl:disp 1.6812e-06 9.8919e-06 0.1700 0.8650This package can only give the marginal effect for each variable in the glm model, but not the average marginal effect that we might look for.