18 Causal Inference
After all of the mambo jumbo that we have learned so far, I want to now talk about the concept of causality. We usually say that correlation is not causation. Then, what is causation?
One of my favorite books has explained this concept beautifully (Pearl and Mackenzie 2018). And I am just going to quickly summarize the gist of it from my understanding. I hope that it can give you an initial grasp on the concept so that later you can continue to read up and develop a deeper understanding.
It’s important to have a deep understanding regarding the method research. However, one needs to be aware of its limitation. As mentioned in various sections throughout the book, we see that we need to ask experts for number as our baseline or visit literature to gain insight from past research.
Here, we dive in a more conceptual side statistical analysis as a whole, regardless of particular approach.
You probably heard scientists say correlation doesn’t mean causation. There are ridiculous spurious correlations that give a firm grip on what the previous phrase means. The pioneer who tried to use regression to infer causation in social science was Yule (1899) (but it was a fatal attempt where he found relief policy increases poverty). To make a causal inference from statistics, the equation (function form) must be stable under intervention (i.e., variables are manipulated). Statistics is used to be a causality-free enterprise in the past.
Not until the development of path analysis by Sewall Wright in the 1920s that the discipline started to pay attention to causation. Then, it remained dormant until the Causal Revolution (quoted Judea Pearl’s words). This revolution introduced the calculus of causation which includes (1) causal diagrams), and (2) a symbolic language
The world has been using \(P(Y|X)\) (statistics use to derive this), but what we want is to compare the difference between
\(P(Y|do(X))\): treatment group
\(P(Y|do(not-X))\): control group
Hence, we can see a clear difference between \(P(Y|X) \neq P(Y|do(X))\)
The conclusion we want to make from data is counterfactuals: What would have happened had we not do X?
To teach a robot to make inference, we need inference engine
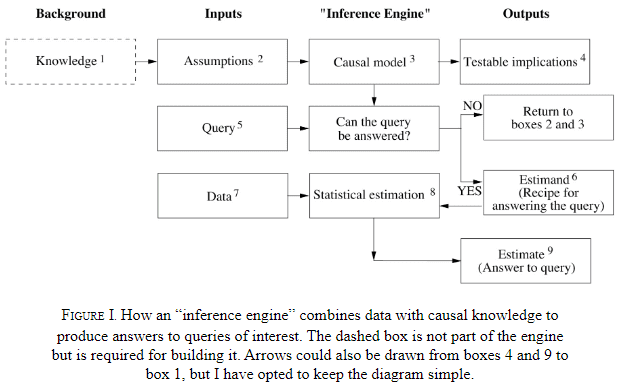
Levels of cognitive ability to be a causal learner:
- Seeing
- Doing
- Imagining
Ladder of causation (associated with levels of cognitive ability as well):
- Association: conditional probability, correlation, regression
- Intervention
- Counterfactuals
| Level | Activity | Questions | Examples |
|---|---|---|---|
|
Association \(P(y|x)\) |
Seeing |
What is? How would seeing X change my belief in Y? |
What does a symptom tell me about a disease? |
|
Intervention \(P(y|do(x),z)\) |
Doing Intervening |
What if? What if I do X? |
What if I spend more time learning, will my result change? |
|
Counterfactuals \(P(y_x|x',y')\) |
Imagining |
Why? What if I had acted differently |
What if I stopped smoking a year ago? |
Table by (Pearl 2019, 57)
You cannot define causation from probability alone
If you say X causes Y if X raises the probability of Y.” On the surface, it might sound intuitively right. But when we translate it to probability notation: \(P(Y|X) >P(Y)\) , it can’t be more wrong. Just because you are seeing X (1st level), it doesn’t mean the probability of Y increases.
It could be either that (1) X causes Y, or (2) Z affects both X and Y. Hence, people might use control variables, which translate: \(P(Y|X, Z=z) > P(Y|Z=z)\), then you can be more confident in your probabilistic observation. However, the question is how can you choose \(Z\)
With the invention of the do-operator, now you can represent X causes Y as
\[ P(Y|do(X)) > P(Y) \]
and with the help of causal diagram, now you can answer questions at the 2nd level (Intervention)
Note: people under econometrics might still use “Granger causality” and “vector autoregression” to use the probability language to represent causality (but it’s not).
The 7 tools for Structural Causal Model framework (Pearl 2019):
Encoding Causal Assumptions - transparency and testability (with graphical representation)
Do-calculus and the control of confounding: “back-door”
The algorithmization of Counterfactuals
Mediation Analysis and the Assessment of Direct and Indirect Effects
Adaptability, External validity and Sample Selection Bias: are still researched under “domain adaptation”, “transfer learning”
Recovering from missing data
-
Causal Discovery:
d-separation
Functional decomposition (Hoyer et al. 2008)
Spontaneous local changes (Pearl 2014)
List of packages to do causal inference in R
Simpson’s Paradox:
- A statistical association seen in an entire population is reversed in sub-population.
Structural Causal Model accompanies graphical causal model to create more efficient language to represent causality
Structural Causal Model is the solution to the curse of dimensionality (i.e., large numbers of variable \(p\), and small dataset \(n\)) thanks to product decomposition. It allows us to solve problems without knowing the function, parameters, or distributions of the error terms.
Suppose you have a causal chain \(X \to Y \to Z\):
\[ P(X=x,Y=y, Z=z) = P(X=x)P(Y=y|X=x)P(Z=z|Y=y) \]
| Experimental Design | Quasi-experimental Design |
|---|---|
| Experimentalist | Observationalist |
| Experimental Data | Observational Data |
| Random Assignment (reduce treatment imbalance) | Random Sampling (reduce sample selection error) |
Criticisms of quasi-experimental versus experimental designs:
-
Quasi-experimental methods don’t approximate well experimental results. For example,
- LaLonde (1986) shows Matching Methods, Difference-in-differences, Tobit-2 (Heckman-type) can’t approximate the experimental estimates.
Tools in a hierarchical order
Experimental Design: Randomized Control Trials (Gold standard): Tier 1
Internal vs. External Validity
Internal Validity: Economists and applied scientists largely care about.
External Validity: Localness might affect your external validity.
For many economic policies, there is a difference between treatment and intention to treat.
For example, we might have an effective vaccine (i.e., intention to treat), but it does not mean that everybody will take it (i.e., treatment).
There are four types of subjects that we deal with:
-
Non-switchers: we don’t care about non-switchers because even if we introduce or don’t introduce the intervention, it won’t affect them.
Always takers
Never takers
-
Switchers
-
Compliers: defined as those who respect the intervention.
We only care about compliers because when we introduce the intervention, they will do something. When we don’t have any interventions, they won’t do it.
Tools above are used to identify the causal impact of an intervention on compliers
If we have only compliers in our dataset, then intention to treatment = treatment effect.
-
Defiers: those who will go to the opposite direction of your treatment.
- We typically aren’t interested in defiers because they will do the opposite of what we want them to do. And they are typically a small group; hence, we just assume they don’t exist.
-
| Treatment Assignment | Control Assignment | |
|---|---|---|
| Compliers | Treated | No Treated |
| Always-takers | Treated | Treated |
| Never-takers | Not treated | No treated |
| Defiers | Not treated | Treated |
Directional Bias due to selection into treatment comes from 2 general opposite sources
- Mitigation-based: select into treatment to combat a problem
- Preference-based: select into treatment because units like that kind of treatment.
18.1 Treatment effect types
This section is based on Paul Testa’s note
Terminology:
Quantities of causal interest (i.e., treatment effect types)
Estimands: parameters of interest
Estimators: procedures to calculate hesitates for the parameters of interest
Sources of bias (according to prof. Luke Keele)
\[ \begin{aligned} &\text{Estimator - True Causal Effect} \\ &= \text{Hidden bias + Misspecification bias + Statistical Noise} \\ &= \text{Due to design + Due to modeling + Due to finite sample} \end{aligned} \]
18.1.1 Average Treatment Effects
Average treatment effect (ATE) is the difference in means of the treated and control groups
Randomization under Experimental Design can provide an unbiased estimate of ATE.
Let \(Y_i(1)\) denote the outcome of individual \(i\) under treatment and
\(Y_i(0)\) denote the outcome of individual \(i\) under control
Then, the treatment effect for individual \(i\) is the difference between her outcome under treatment and control
\[ \tau_i = Y_i(1) - Y_i(0) \]
Without a time machine or dimension portal, we can only observe one of the two event: either individual \(i\) experiences the treatment or she doesn’t.
Then, the ATE as a quantity of interest can come in handy since we can observe across all individuals
\[ ATE = \frac{1}{N} \sum_{i=1}^N \tau_i = \frac{\sum_1^N Y_i(1)}{N} - \frac{\sum_i^N Y_i(0)}{N} \]
With random assignment (i.e., treatment assignment is independent of potential outcome and observables and unobservables), the observed means difference between the two groups is an unbiased estimator of the average treatment effect
\[ E(Y_i (1) |D = 1) = E(Y_i(1)|D=0) = E(Y_i(1)) \\ E(Y_i(0) |D = 1) = E(Y_i(0)|D = 0 ) = E(Y_i(0)) \]
\[ ATE = E(Y_i(1)) - E(Y_i(0)) \]
Alternatively, we can write the potential outcomes model in a regression form
\[ Y_i = Y_i(0) + [Y_i (1) - Y_i(0)] D_i \]
Let \(\beta_{0i} = Y_i (0) ; \beta_{1i} = Y_i(1) - Y_i(0)\), we have
\[ Y_i = \beta_{0i} + \beta_{1i} D_i \]
where
\(\beta_{0i}\) = outcome if the unit did not receive any treatment
\(\beta_{1i}\) = treatment effect (i.e., random coefficients for each unit \(i\))
To understand endogeneity (i.e., nonrandom treatment assignment), we can examine a standard linear model
\[ \begin{aligned} Y_i &= \beta_{0i} + \beta_{1i} D_i \\ &= ( \bar{\beta}_{0} + \epsilon_{0i} ) + (\bar{\beta}_{1} + \epsilon_{1i} )D_i \\ &= \bar{\beta}_{0} + \epsilon_{0i} + \bar{\beta}_{1} D_i + \epsilon_{1i} D_i \end{aligned} \]
When you have random assignment, \(E(\epsilon_{0i}) = E(\epsilon_{1i}) = 0\)
No selection bias: \(D_i \perp e_{0i}\)
Treatment effect is independent of treatment assignment: \(D_i \perp e_{1i}\)
But otherwise, residuals can correlate with \(D_i\)
For estimation,
\(\hat{\beta}_1^{OLS}\) is identical to difference in means (i.e., \(Y_i(1) - Y_i(0)\))
-
In case of heteroskedasticity (i.e., \(\epsilon_{0i} + D_i \epsilon_{1i} \neq 0\) ), this residual’s variance depends on \(X\) when you have heterogeneous treatment effects (i.e., \(\epsilon_{1i} \neq 0\))
Robust SE should still give consistent estimate of \(\hat{\beta}_1\) in this case
Alternatively, one can use two-sample t-test on difference in means with unequal variances.
18.1.2 Conditional Average Treatment Effects
Treatment effects can be different for different groups of people. In words, treatment effects can vary across subgroups.
To examine the heterogeneity across groups (e.g., men vs. women), we can estimate the conditional average treatment effects (CATE) for each subgroup
\[ CATE = E(Y_i(1) - Y_i(0) |D_i, X_i)) \]
18.1.3 Intent-to-treat Effects
When we encounter non-compliance (either people suppose to receive treatment don’t receive it, or people suppose to be in the control group receive the treatment), treatment receipt is not independent of potential outcomes and confounders.
In this case, the difference in observed means between the treatment and control groups is not Average Treatment Effects, but Intent-to-treat Effects (ITT). In words, ITT is the treatment effect on those who receive the treatment
18.1.4 Local Average Treatment Effects
Instead of estimating the treatment effects of those who receive the treatment (i.e., Intent-to-treat Effects), you want to estimate the treatment effect of those who actually comply with the treatment. This is the local average treatment effects (LATE) or complier average causal effects (CACE). I assume we don’t use CATE to denote complier average treatment effect because it was reserved for conditional average treatment effects.
- Using random treatment assignment as an instrument, we can recover the effect of treatment on compliers.
As the percent of compliers increases, Intent-to-treat Effects and Local Average Treatment Effects converge
Rule of thumb: SE(LATE) = SE(ITT)/(share of compliers)
LATE estimate is always greater than the ITT estimate
LATE can also be estimated using a pure placebo group (Gerber et al. 2010).
Partial compliance is hard to study, and IV/2SLS estimator is biased, we have to use Bayesian (Long, Little, and Lin 2010; Jin and Rubin 2009, 2008).
18.1.4.1 One-sided noncompliance
One-sided noncompliance is when in the sample, we only have compliers and never-takers
With the exclusion restriction (i.e., excludability), never-takers have the same results in the treatment or control group (i.e., never treated)
With random assignment, we can have the same number of never-takers in the treatment and control groups
Hence,
\[ LATE = \frac{ITT}{\text{share of compliers}} \]
18.1.4.2 Two-sided noncompliance
Two-sided noncompliance is when in the sample, we have compliers, never-takers, and always-takers
To estimate LATE, beyond excludability like in the One-sided noncompliance case, we need to assume that there is no defiers (i.e., monotonicity assumption) (this is excusable in practical studies)
\[ LATE = \frac{ITT}{\text{share of compliers}} \]
18.1.5 Population vs. Sample Average Treatment Effects
See (Imai, King, and Stuart 2008) for when the sample average treatment effect (SATE) diverges from the population average treatment effect (PATE).
To stay consistent, this section uses notations from (Imai, King, and Stuart 2008)’s paper.
In a finite population \(N\), we observe \(n\) observations (\(N>>n\)), where half is in the control and half is in the treatment group.
With unknown data generating process, we have
\[ I_i = \begin{cases} 1 \text{ if unit i is in the sample} \\ 0 \text{ otherwise} \end{cases} \]
\[ T_i = \begin{cases} 1 \text{ if unit i is in the treatment group} \\ 0 \text{ if unit i is in the control group} \end{cases} \]
\[ \text{potential outcome} = \begin{cases} Y_i(1) \text{ if } T_i = 1 \\ Y_i(0) \text{ if } T_i = 0 \end{cases} \]
Observed outcome is
\[ Y_i | I_i = 1= T_i Y_i(1) + (1-T_i)Y_i(0) \]
Since we can never observed both outcome for the same individual, the treatment effect is always unobserved for unit \(i\)
\[ TE_i = Y_i(1) - Y_i(0) \]
Sample average treatment effect is
\[ SATE = \frac{1}{n}\sum_{i \in \{I_i = 1\}} TE_i \]
Population average treatment effect is
\[ PATE = \frac{1}{N}\sum_{i=1}^N TE_i \]
Let \(X_i\) be observables and \(U_i\) be unobservables for unit \(i\)
The baseline estimator for SATE and PATE is
\[ \begin{aligned} D &= \frac{1}{n/2} \sum_{i \in (I_i = 1, T_i = 1)} Y_i - \frac{1}{n/2} \sum_{i \in (I_i = 1 , T_i = 0)} Y_i \\ &= \text{observed sample mean of the treatment group} \\ &- \text{observed sample mean of the control group} \end{aligned} \]
Let \(\Delta\) be the estimation error (deviation from the truth), under an additive model
\[ Y_i(t) = g_t(X_i) + h_t(U_i) \]
The decomposition of the estimation error is
\[ \begin{aligned} PATE - D = \Delta &= \Delta_S + \Delta_T \\ &= (PATE - SATE) + (SATE - D)\\ &= \text{sample selection}+ \text{treatment imbalance} \\ &= (\Delta_{S_X} + \Delta_{S_U}) + (\Delta_{T_X} + \Delta_{T_U}) \\ &= \text{(selection on observed + selection on unobserved)} \\ &+ (\text{treatment imbalance in observed + unobserved}) \end{aligned} \]
18.1.5.1 Estimation Error from Sample Selection
Also known as sample selection error
\[ \Delta_S = PATE - SATE = \frac{N - n}{N}(NATE - SATE) \]
where NATE is the non-sample average treatment effect (i.e., average treatment effect for those in the population but not in your sample:
\[ NATE = \sum_{i\in (I_i = 0)} \frac{TE_i}{N-n} \]
From the equation, to have zero sample selection error (i.e., \(\Delta_S = 0\)), we can either
Get \(N = n\) by redefining your sample as the population of interest
\(NATE = SATE\) (e.g., \(TE_i\) is constant over \(i\) in both your selected sample, and those in the population that you did not select)
Note
When you have heterogeneous treatment effects, random sampling can only warrant sample selection bias, not sample selection error.
-
Since we can rarely know the true underlying distributions of the observables (\(X\)) and unobservables (\(U\)), we cannot verify whether the empirical distributions of your observables and unobservables for those in your sample is identical to that of your population (to reduce \(\Delta_S\)). For special case,
Say you have census of your population, you can adjust for the observables \(X\) to reduce \(\Delta_{S_X}\), but still you cannot adjust your unobservables (\(U\))
-
Say you are willing to assume \(TE_i\) is constant over
\(X_i\), then \(\Delta_{S_X} = 0\)
\(U_i\), then \(\Delta_{U}=0\)
18.1.5.2 Estimation Error from Treatment Imbalance
Also known as treatment imbalance error
\[ \Delta_T = SATE - D \]
\(\Delta_T \to 0\) when treatment and control groups are balanced (i.e., identical empirical distributions) for both observables (\(X\)) and unobservables (\(U\))
However, in reality, we can only readjust for observables, not unobservables.
| Blocking | Matching Methods | |
|---|---|---|
| Definition | Random assignment within strata based on pre-treatment observables | Dropping, repeating or grouping observations to balance covariates between the treatment and control group (Rubin 1973) |
| Time | Before randomization of treatments | After randomization of treatments |
| What if the set of covariates used to adjust is irrelevant? | Nothing happens | In the worst case scenario (e.g., these variables are uncorrelated with the treatment assignment, but correlated with the post-treatment variables), matching induces bias that is greater than just using the unadjusted difference in means |
| Benefits | \(\Delta_{T_X}=0\) (no imbalance on observables). But we don’t know its effect on unobservables imbalance (might reduce if the unobservables are correlated with the observables) | Reduce model dependence, bias, variance, mean-square error |
18.1.6 Average Treatment Effects on the Treated and Control
Average Effect of treatment on the Treated (ATT) is
\[ \begin{aligned} ATT &= E(Y_i(1) - Y_i(0)|D_i = 1) \\ &= E(Y_i(1)|D_i = 1) - E(Y_i(0) |D_i = 1) \end{aligned} \]
Average Effect of treatment on the Control (ATC) (i.e., the effect would be for those weren’t treated) is
\[ \begin{aligned} ATC &= E(Y_i(1) - Y_i (0) |D_i =0) \\ &= E(Y_i(1)|D_i = 0) - E(Y_i(0)|D_i = 0) \end{aligned} \]
Under random assignment and full compliance,
\[ ATE = ATT = ATC \]
Sample average treatment effect on the treated is
\[ SATT = \frac{1}{n} \sum_i TE_i \]
where
\(TE_i\) is the treatment effect for unit \(i\)
\(n\) is the number of treated units in the sample
\(i\) belongs the subset (i.e., sample) of the population of interest that is treated.
Population average treatment effect on the treated is
\[ PATT = \frac{1}{N} \sum_i TE_i \]
where
\(TE_i\) is the treatment effect for unit \(i\)
\(N\) is the number of treated units in the population
\(i\) belongs to the population of interest that is treated.
18.1.7 Quantile Average Treatment Effects
Instead of the middle point estimate (ATE), we can also understand the changes in the distribution the outcome variable due to the treatment.
Using quantile regression and more assumptions (Abadie, Angrist, and Imbens 2002; Chernozhukov and Hansen 2005), we can have consistent estimate of quantile treatment effects (QTE), with which we can make inference regarding a given quantile.
18.1.8 Mediation Effects
With additional assumptions (i.e., sequential ignorability (Imai, Keele, and Tingley 2010; Bullock and Ha 2011)), we can examine the mechanism of the treatment on the outcome.
Under the causal framework,
the indirect effect of treatment via a mediator is called average causal mediation effect (ACME)
the direct effect of treatment on outcome is the average direct effect (ADE)
18.1.9 Log-odds Treatment Effects
For binary outcome variable, we might be interested in the log-odds of success. See (Freedman 2008) on how to estimate a consistent causal effect.
Alternatively, attributable effects (Rosenbaum 2002) can also be appropriate for binary outcome.