32.14 Applications
32.14.1 Synthetic Control Estimation
This example simulates data for 10 states over 30 years, where State A receives treatment after year 15. We implement two approaches:
- Standard Synthetic Control using
Synth. - Generalized Synthetic Control using
gsynth, which incorporates iterative fixed effects and multiple treated units.
Load Required Libraries
We construct a panel dataset where the outcome variable \(Y\) is influenced by two covariates (\(X_1, X_2\)). Treatment (\(T\)) is applied to State A from year 15 onwards, with an artificial treatment effect of +20.
# Simulate panel data
set.seed(1)
df <- data.frame(
year = rep(1:30, 10), # 30 years for 10 states
state = rep(LETTERS[1:10], each = 30), # States A to J
X1 = round(rnorm(300, 2, 1), 2), # Continuous covariate
X2 = round(rbinom(300, 1, 0.5) + rnorm(300), 2), # Binary + noise
state.num = rep(1:10, each = 30) # Numeric identifier for states
)
# Outcome variable: Y = 1 + 2 * X1 + noise
df$Y <- round(1 + 2 * df$X1 + rnorm(300), 2)
# Assign treatment: Only State A (state == "A") from year 15 onward
df$T <- as.integer(df$state == "A" & df$year >= 15)
# Apply treatment effect: Increase Y by 20 where treatment is applied
df$Y[df$T == 1] <- df$Y[df$T == 1] + 20
# View data structure
str(df)
#> 'data.frame': 300 obs. of 7 variables:
#> $ year : int 1 2 3 4 5 6 7 8 9 10 ...
#> $ state : chr "A" "A" "A" "A" ...
#> $ X1 : num 1.37 2.18 1.16 3.6 2.33 1.18 2.49 2.74 2.58 1.69 ...
#> $ X2 : num 1.96 0.4 -0.75 -0.56 -0.45 1.06 0.51 -2.1 0 0.54 ...
#> $ state.num: int 1 1 1 1 1 1 1 1 1 1 ...
#> $ Y : num 2.29 4.51 2.07 8.87 4.37 1.32 8 7.49 6.98 3.72 ...
#> $ T : int 0 0 0 0 0 0 0 0 0 0 ...Step 1: Estimating Synthetic Control with Synth
The Synth package creates a synthetic control by matching pre-treatment trends of the treated unit (State A) with a weighted combination of donor states.
We specify predictors, dependent variable, and donor pool.
dataprep.out <- dataprep(
df,
predictors = c("X1", "X2"),
dependent = "Y",
unit.variable = "state.num",
time.variable = "year",
unit.names.variable = "state",
treatment.identifier = 1,
controls.identifier = 2:10,
time.predictors.prior = 1:14,
time.optimize.ssr = 1:14,
time.plot = 1:30
)Fit Synthetic Control Model
synth.out <- synth(dataprep.out)
#>
#> X1, X0, Z1, Z0 all come directly from dataprep object.
#>
#>
#> ****************
#> searching for synthetic control unit
#>
#>
#> ****************
#> ****************
#> ****************
#>
#> MSPE (LOSS V): 9.831789
#>
#> solution.v:
#> 0.3888387 0.6111613
#>
#> solution.w:
#> 0.1115941 0.1832781 0.1027237 0.312091 0.06096758 0.03509706 0.05893735 0.05746256 0.07784853
# Display synthetic control weights and balance table
print(synth.tab(dataprep.res = dataprep.out, synth.res = synth.out))
#> $tab.pred
#> Treated Synthetic Sample Mean
#> X1 2.028 2.028 2.017
#> X2 0.513 0.513 0.394
#>
#> $tab.v
#> v.weights
#> X1 0.389
#> X2 0.611
#>
#> $tab.w
#> w.weights unit.names unit.numbers
#> 2 0.112 B 2
#> 3 0.183 C 3
#> 4 0.103 D 4
#> 5 0.312 E 5
#> 6 0.061 F 6
#> 7 0.035 G 7
#> 8 0.059 H 8
#> 9 0.057 I 9
#> 10 0.078 J 10
#>
#> $tab.loss
#> Loss W Loss V
#> [1,] 9.761708e-12 9.831789Plot: Observed vs. Synthetic State A
path.plot(
synth.out,
dataprep.out,
Ylab = "Y",
Xlab = "Year",
Legend = c("State A", "Synthetic State A"),
Legend.position = "topleft"
)
# Mark the treatment start year
abline(v = 15, lty = 2) 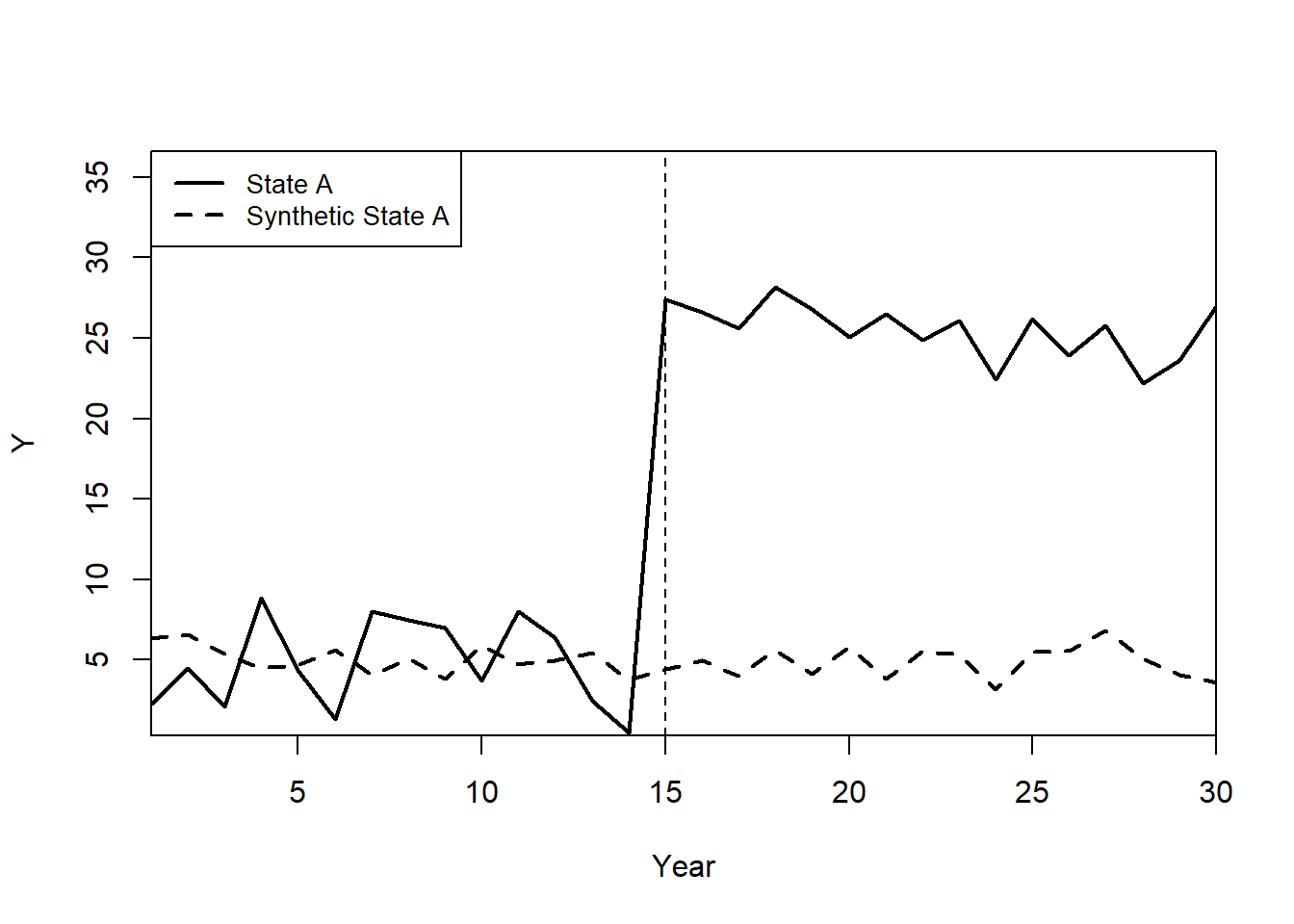
Plot: Treatment Effect (Gaps Plot)
The gaps plot shows the difference between State A and its synthetic control over time.
gaps.plot(synth.res = synth.out,
dataprep.res = dataprep.out,
Ylab = c("Gap"),
Xlab = c("Year"),
Ylim = c(-30, 30),
Main = ""
)
abline(v = 15, lty = 2)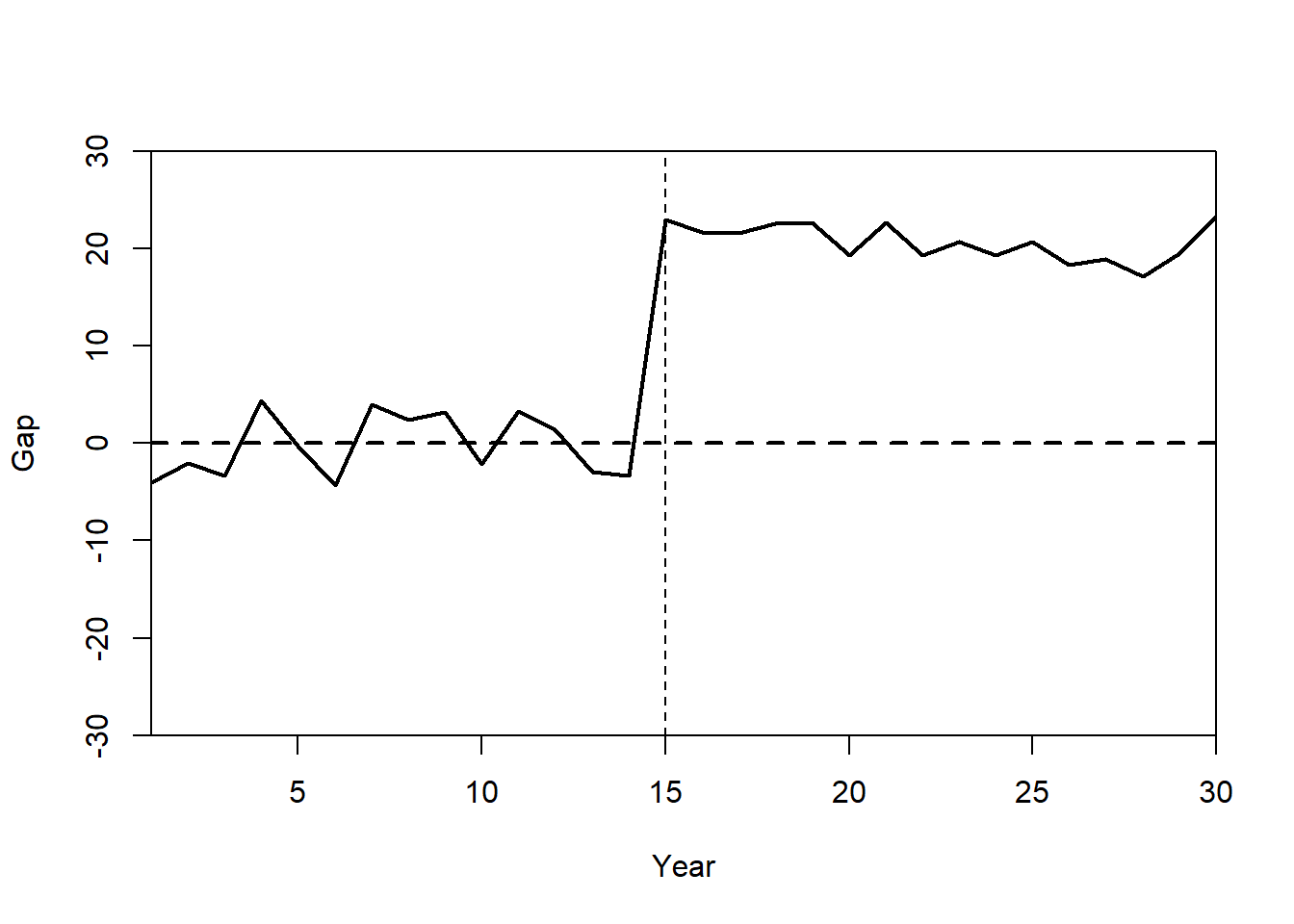
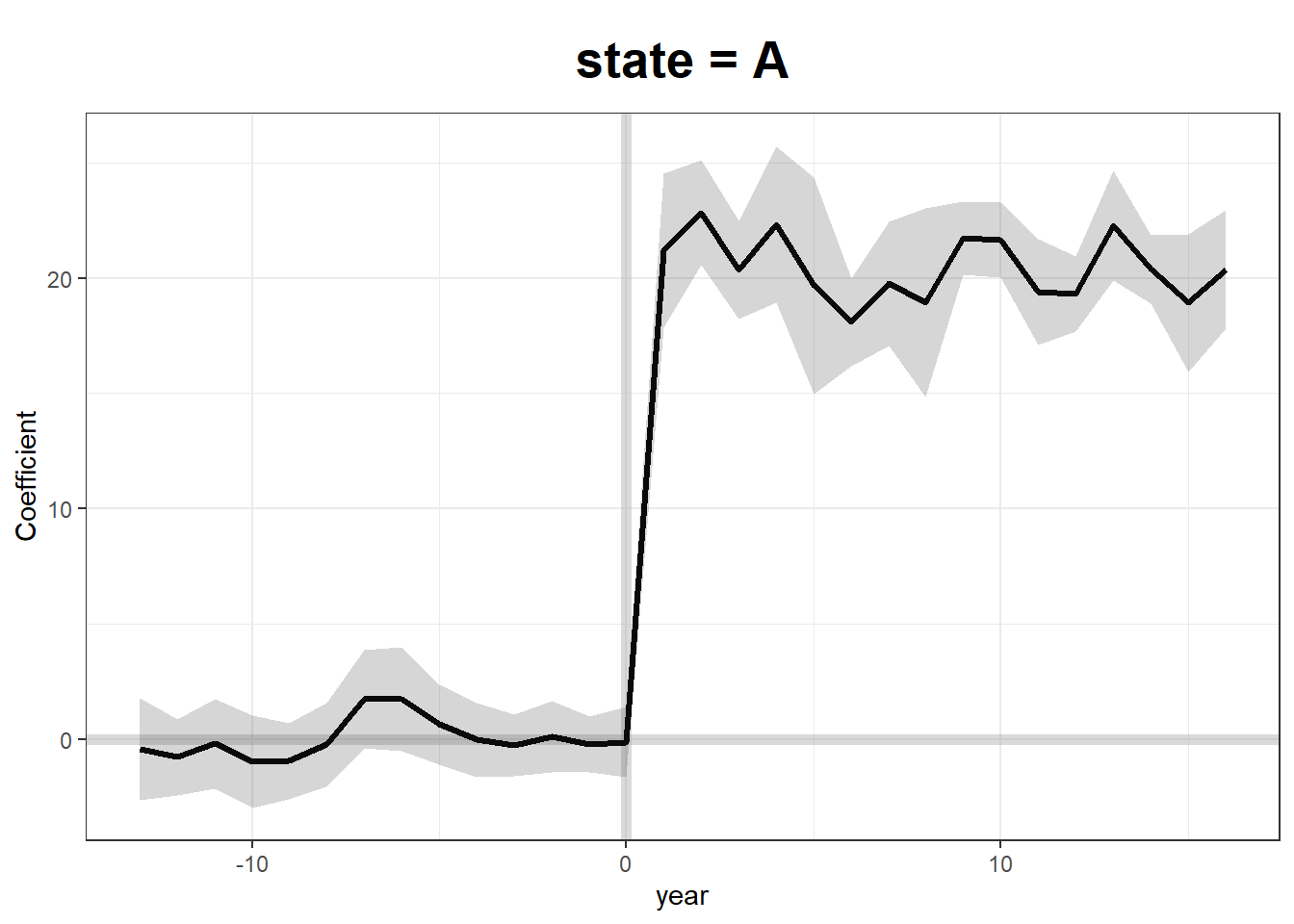
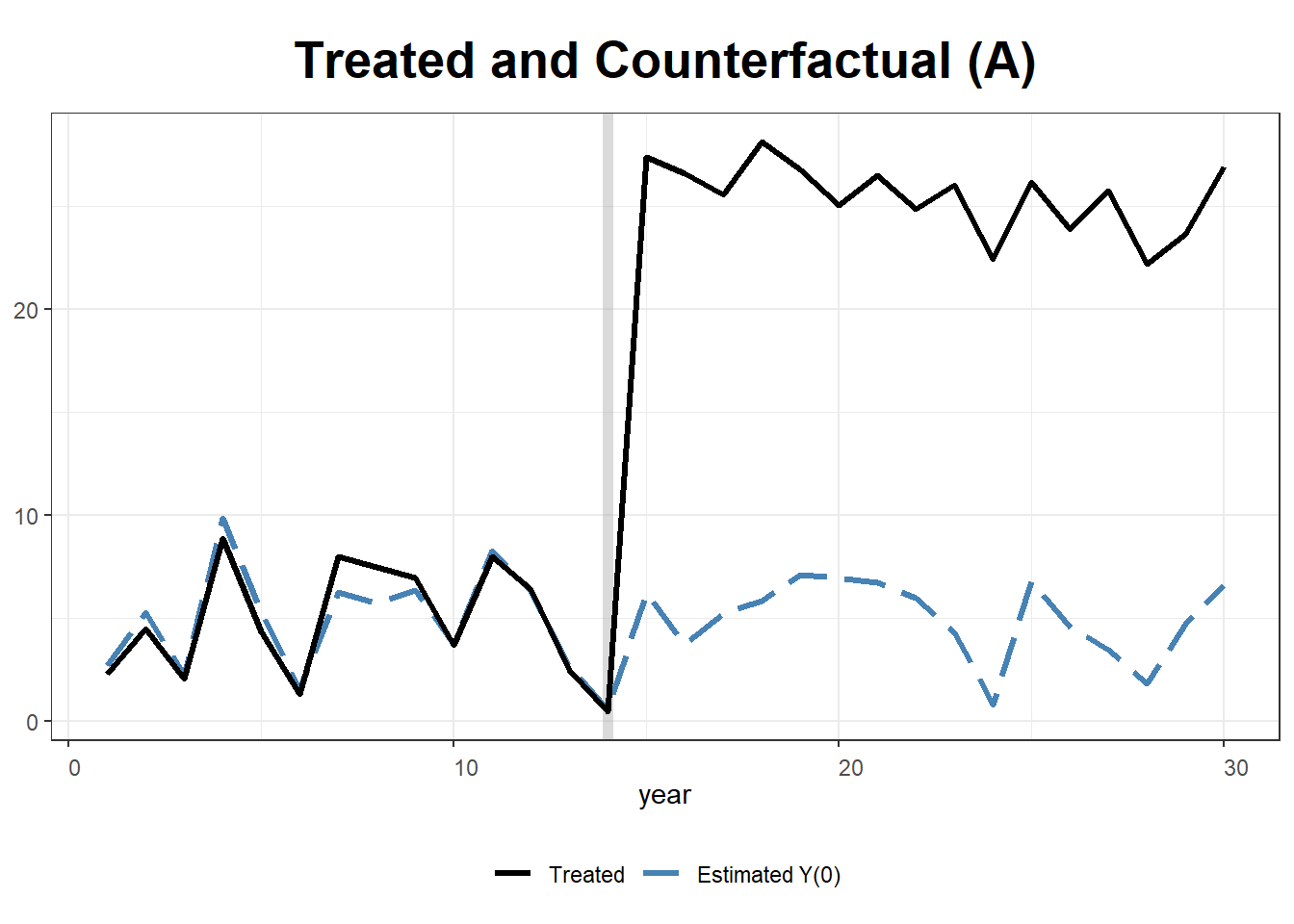
Step 2: Estimating Generalized Synthetic Control with gsynth
Unlike Synth, the gsynth package supports:
Iterative Fixed Effects (IFE) for unobserved heterogeneity.
Multiple Treated Units and Staggered Adoption.
Bootstrapped Standard Errors for inference.
Fit Generalized Synthetic Control Model
We use two-way fixed effects, cross-validation (CV = TRUE), and bootstrapped standard errors.
gsynth.out <- gsynth(
Y ~ T + X1 + X2,
data = df,
index = c("state", "year"),
force = "two-way",
CV = TRUE,
r = c(0, 5),
se = TRUE,
inference = "parametric",
nboots = 100
)
#> Parallel computing ...
#> Cross-validating ...
#> r = 0; sigma2 = 1.13533; IC = 0.95632; PC = 0.96713; MSPE = 1.65502
#> r = 1; sigma2 = 0.96885; IC = 1.54420; PC = 4.30644; MSPE = 1.33375
#> r = 2; sigma2 = 0.81855; IC = 2.08062; PC = 6.58556; MSPE = 1.27341*
#> r = 3; sigma2 = 0.71670; IC = 2.61125; PC = 8.35187; MSPE = 1.79319
#> r = 4; sigma2 = 0.62823; IC = 3.10156; PC = 9.59221; MSPE = 2.02301
#> r = 5; sigma2 = 0.55497; IC = 3.55814; PC = 10.48406; MSPE = 2.79596
#>
#> r* = 2
#>
#>
Simulating errors ...
Bootstrapping ...
#> 
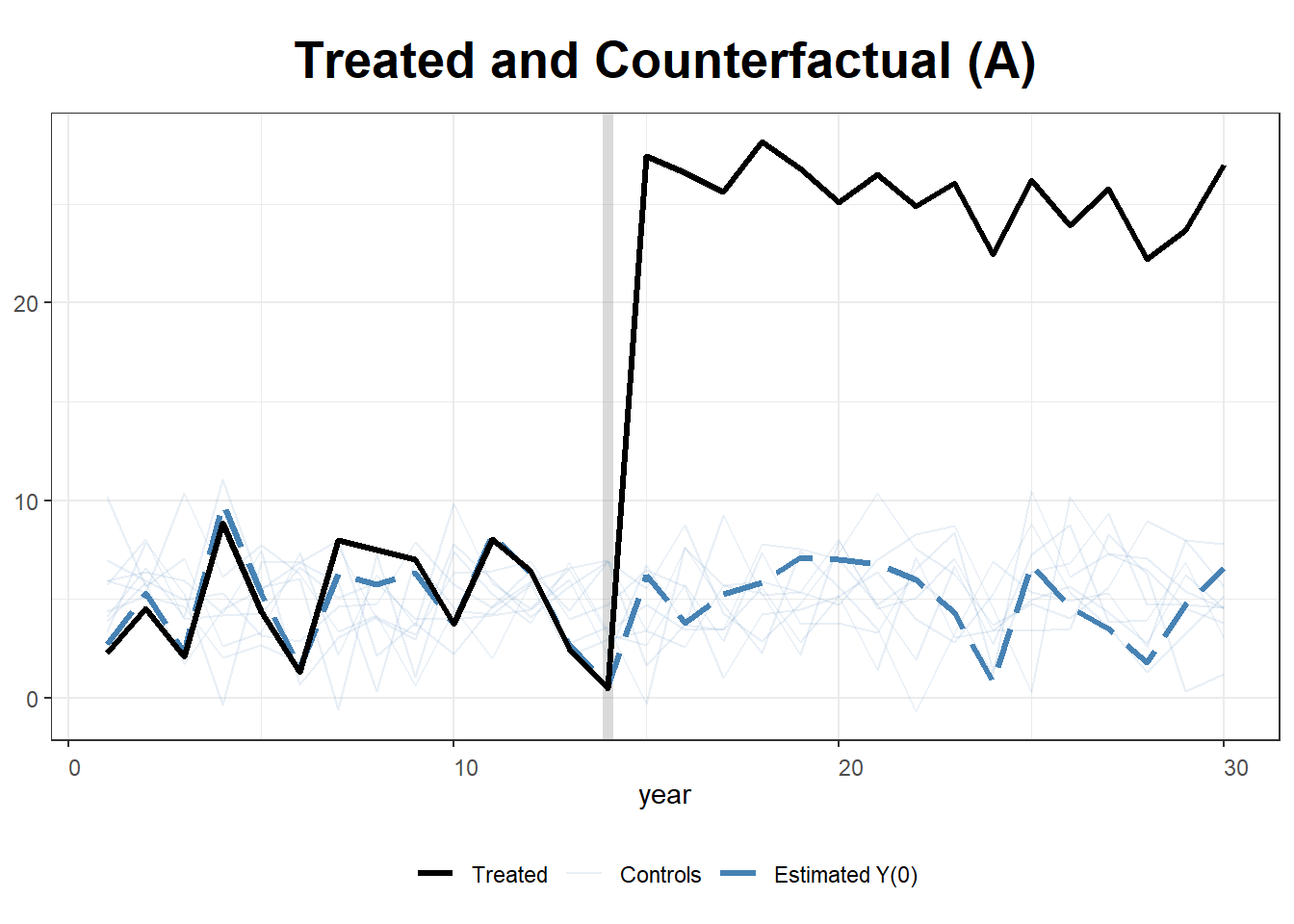
32.14.2 The Basque Country Policy Change
The Basque Country in Spain implemented a major policy change in 1975, impacting its GDP per capita growth. This example uses SCM to estimate the counterfactual economic performance had the policy not been implemented.
We will:
- Construct a synthetic control using economic predictors. 2
- Evaluate the policy’s impact by comparing the real and synthetic Basque GDP.
The basque dataset from Synth contains economic indicators for Spain’s regions from 1955 to 1997.
data("basque")
dim(basque) # 774 observations, 17 variables
#> [1] 774 17
head(basque)
#> regionno regionname year gdpcap sec.agriculture sec.energy sec.industry
#> 1 1 Spain (Espana) 1955 2.354542 NA NA NA
#> 2 1 Spain (Espana) 1956 2.480149 NA NA NA
#> 3 1 Spain (Espana) 1957 2.603613 NA NA NA
#> 4 1 Spain (Espana) 1958 2.637104 NA NA NA
#> 5 1 Spain (Espana) 1959 2.669880 NA NA NA
#> 6 1 Spain (Espana) 1960 2.869966 NA NA NA
#> sec.construction sec.services.venta sec.services.nonventa school.illit
#> 1 NA NA NA NA
#> 2 NA NA NA NA
#> 3 NA NA NA NA
#> 4 NA NA NA NA
#> 5 NA NA NA NA
#> 6 NA NA NA NA
#> school.prim school.med school.high school.post.high popdens invest
#> 1 NA NA NA NA NA NA
#> 2 NA NA NA NA NA NA
#> 3 NA NA NA NA NA NA
#> 4 NA NA NA NA NA NA
#> 5 NA NA NA NA NA NA
#> 6 NA NA NA NA NA NAStep 1: Preparing Data for Synth
We define predictors and specify pre-treatment (1960–1969) and post-treatment (1975–1997) periods.
dataprep.out <- dataprep(
foo = basque,
predictors = c(
"school.illit",
"school.prim",
"school.med",
"school.high",
"school.post.high",
"invest"
),
predictors.op = "mean",
time.predictors.prior = 1964:1969,
# Pre-treatment period
special.predictors = list(
list("gdpcap", 1960:1969, "mean"),
list("sec.agriculture", seq(1961, 1969, 2), "mean"),
list("sec.energy", seq(1961, 1969, 2), "mean"),
list("sec.industry", seq(1961, 1969, 2), "mean"),
list("sec.construction", seq(1961, 1969, 2), "mean"),
list("sec.services.venta", seq(1961, 1969, 2), "mean"),
list("sec.services.nonventa", seq(1961, 1969, 2), "mean"),
list("popdens", 1969, "mean")
),
dependent = "gdpcap",
unit.variable = "regionno",
unit.names.variable = "regionname",
time.variable = "year",
treatment.identifier = 17,
# Basque region
controls.identifier = c(2:16, 18),
# Control regions
time.optimize.ssr = 1960:1969,
time.plot = 1955:1997
)Step 2: Estimating the Synthetic Control
We now estimate the synthetic control weights using synth(). This solves for weights that best match the pre-treatment economic indicators of the Basque Country.
synth.out = synth(data.prep.obj = dataprep.out, method = "BFGS")
#>
#> X1, X0, Z1, Z0 all come directly from dataprep object.
#>
#>
#> ****************
#> searching for synthetic control unit
#>
#>
#> ****************
#> ****************
#> ****************
#>
#> MSPE (LOSS V): 0.008864606
#>
#> solution.v:
#> 0.02773094 1.194e-07 1.60609e-05 0.0007163836 1.486e-07 0.002423908 0.0587055 0.2651997 0.02851006 0.291276 0.007994382 0.004053188 0.009398579 0.303975
#>
#> solution.w:
#> 2.53e-08 4.63e-08 6.44e-08 2.81e-08 3.37e-08 4.844e-07 4.2e-08 4.69e-08 0.8508145 9.75e-08 3.2e-08 5.54e-08 0.1491843 4.86e-08 9.89e-08 1.162e-07Step 3: Evaluating Treatment Effects
Calculate the GDP Gap Between Real and Synthetic Basque Country
gaps = dataprep.out$Y1plot - (dataprep.out$Y0plot %*% synth.out$solution.w)
gaps[1:3,1] # First three differences
#> 1955 1956 1957
#> 0.15023473 0.09168035 0.03716475The synth.tab() function provides pre-treatment fit diagnostics and predictor weights.
synth.tables = synth.tab(dataprep.res = dataprep.out, synth.res = synth.out)
names(synth.tables)
#> [1] "tab.pred" "tab.v" "tab.w" "tab.loss"
# Predictor Balance Table
synth.tables$tab.pred[1:13,]
#> Treated Synthetic Sample Mean
#> school.illit 39.888 256.337 170.786
#> school.prim 1031.742 2730.104 1127.186
#> school.med 90.359 223.340 76.260
#> school.high 25.728 63.437 24.235
#> school.post.high 13.480 36.153 13.478
#> invest 24.647 21.583 21.424
#> special.gdpcap.1960.1969 5.285 5.271 3.581
#> special.sec.agriculture.1961.1969 6.844 6.179 21.353
#> special.sec.energy.1961.1969 4.106 2.760 5.310
#> special.sec.industry.1961.1969 45.082 37.636 22.425
#> special.sec.construction.1961.1969 6.150 6.952 7.276
#> special.sec.services.venta.1961.1969 33.754 41.104 36.528
#> special.sec.services.nonventa.1961.1969 4.072 5.371 7.111Importance of Each Control Region in the Synthetic Basque Country
synth.tables$tab.w[8:14, ]
#> w.weights unit.names unit.numbers
#> 9 0.000 Castilla-La Mancha 9
#> 10 0.851 Cataluna 10
#> 11 0.000 Comunidad Valenciana 11
#> 12 0.000 Extremadura 12
#> 13 0.000 Galicia 13
#> 14 0.149 Madrid (Comunidad De) 14
#> 15 0.000 Murcia (Region de) 15Step 4: Visualizing Results
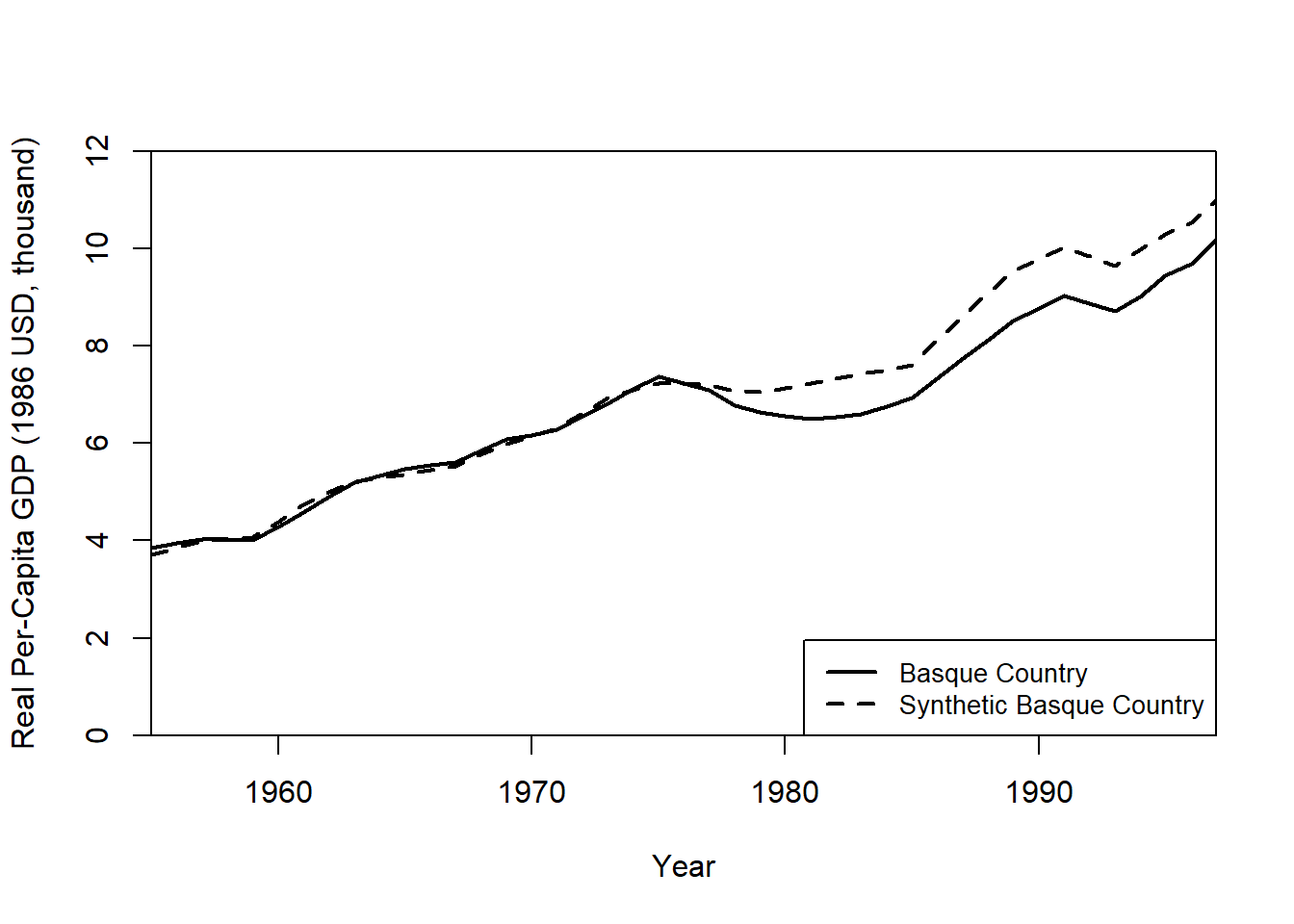
Plot Real vs. Synthetic GDP Per Capita
path.plot(
synth.res = synth.out,
dataprep.res = dataprep.out,
Ylab = "Real Per-Capita GDP (1986 USD, thousand)",
Xlab = "Year",
Ylim = c(0, 12),
Legend = c("Basque Country", "Synthetic Basque Country"),
Legend.position = "bottomright"
)
Plot the Treatment Effect (GDP Gap)
gaps.plot(
synth.res = synth.out,
dataprep.res = dataprep.out,
Ylab = "Gap in Real Per-Capita GDP (1986 USD, thousand)",
Xlab = "Year",
Ylim = c(-1.5, 1.5),
Main = NA
)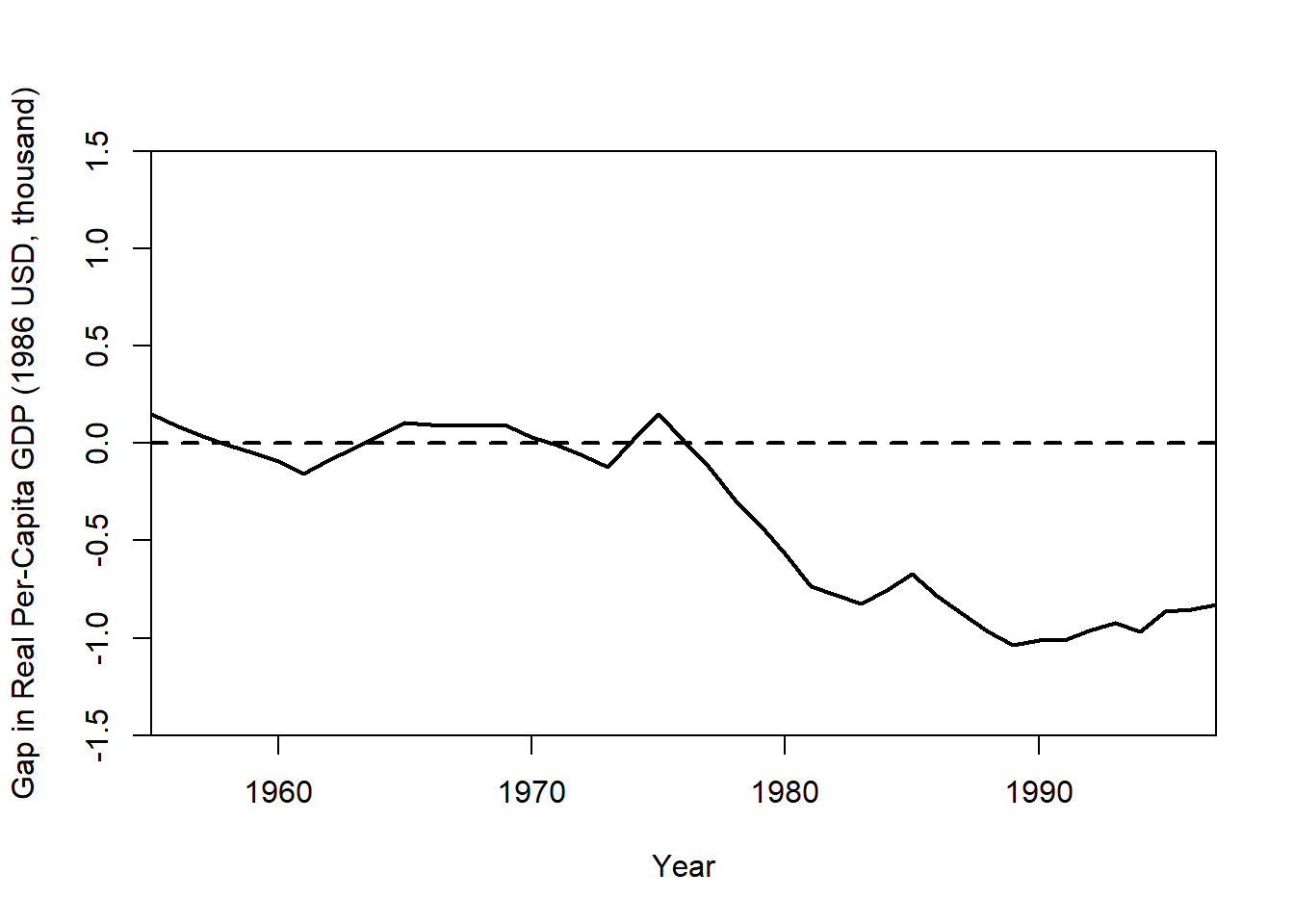
The gap plot shows the difference between actual Basque GDP and its synthetic control over time. A large post-treatment deviation suggests a policy impact.
32.14.3 Micro-Synthetic Control with microsynth
The microsynth package extends standard SCM by allowing: 1
- Matching on both predictors and time-variant outcomes. 2
- Permutation tests and jackknife resampling for placebo tests.
- Multiple follow-up periods to track long-term treatment effects.
- Omnibus test statistics for multiple outcome variables.
This example evaluates the Seattle Drug Market Initiative, a policing intervention aimed at reducing drug-related crime. The dataset seattledmi contains crime statistics across different city zones.
Step 1: Load the Required Package and Data
Step 2: Define Predictors and Outcome Variables
We specify:
Predictors (time-invariant): Population, race distribution, household data.
Outcomes (time-variant): Crime rates across different offense categories.
cov.var <- c(
"TotalPop",
"BLACK",
"HISPANIC",
"Males_1521",
"HOUSEHOLDS",
"FAMILYHOUS",
"FEMALE_HOU",
"RENTER_HOU",
"VACANT_HOU"
)
match.out <- c("i_felony", "i_misdemea", "i_drugs", "any_crime")Step 3: Fit the Micro-Synthetic Control Model
We first estimate treatment effects using a single follow-up period.
sea1 <- microsynth(
seattledmi,
idvar = "ID", # Unique unit identifier
timevar = "time", # Time variable
intvar = "Intervention",# Treatment assignment
start.pre = 1, # Start of pre-treatment period
end.pre = 12, # End of pre-treatment period
end.post = 16, # End of post-treatment period
match.out = match.out, # Outcomes to match on
match.covar = cov.var, # Predictors to match on
result.var = match.out, # Variables for treatment effect estimates
omnibus.var = match.out, # Variables for omnibus p-values
test = "lower", # One-sided test (decrease in crime)
n.cores = min(parallel::detectCores() - 4, 2) # Parallel processing
)Step 4: Summarize Results
This output provides:
Weighted unit contributions to the synthetic control.
Treatment effect estimates and confidence intervals.
p-values from permutation tests.
Step 5: Visualize the Treatment Effect
We generate a treatment effect plot comparing actual vs. synthetic trends.
Step 6: Incorporating Multiple Follow-Up Periods
We extend the analysis by adding multiple post-treatment periods (end.post = c(14, 16)) and permutation-based placebo tests (perm = 250, jack = TRUE).
sea2 <- microsynth(
seattledmi,
idvar = "ID",
timevar = "time",
intvar = "Intervention",
start.pre = 1,
end.pre = 12,
end.post = c(14, 16), # Two follow-up periods
match.out = match.out,
match.covar = cov.var,
result.var = match.out,
omnibus.var = match.out,
test = "lower",
perm = 250, # Permutation placebo tests
jack = TRUE, # Jackknife resampling
n.cores = min(parallel::detectCores() - 4, 2)
)Step 7: Placebo Testing and Robustness Checks
Permutation and jackknife tests assess whether observed treatment effects are statistically significant or due to random fluctuations.
Key robustness checks:
- Permutation Tests (
perm = 250)
1. Reassigns treatment randomly and estimates placebo effects
2. If true effects exceed placebo effects, they are likely causal.- Jackknife Resampling (
jack = TRUE)
1. Removes one control unit at a time and re-estimates effects.
2. Ensures no single control dominates the synthetic match.