14.1 Types of hypothesis testing

\(H_0 : \theta = \theta_0\)

\(H_1 : \theta \neq \theta_0\)

How far away / extreme \(\theta\) can be if our null hypothesis is true

Assume that our likelihood function for q is \(L(q) = q^{30}(1-q)^{70}\) Likelihood function

q = seq(0, 1, length = 100)
L = function(q) {
    q ^ 30 * (1 - q) ^ 70
}

plot(q,
     L(q),
     ylab = "L(q)",
     xlab = "q",
     type = "l")

Log-Likelihood function

q = seq(0, 1, length = 100)
l = function(q) {
    30 * log(q) + 70 * log(1 - q)
}
plot(q,
     l(q) - l(0.3),
     ylab = "l(q) - l(qhat)",
     xlab = "q",
     type = "l")
abline(v = 0.2)

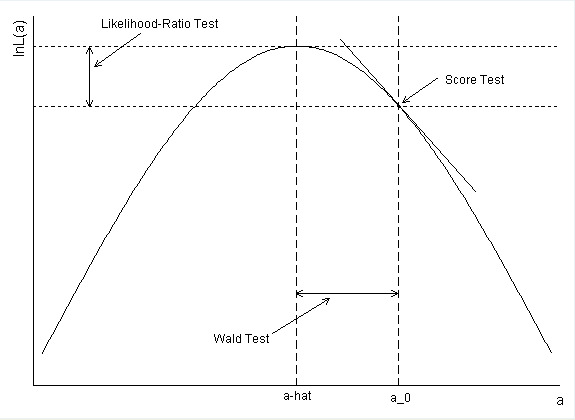
Figure from(Fox 1997)

typically, The likelihood ratio test (and Lagrange Multiplier (Score)) performs better with small to moderate sample sizes, but the Wald test only requires one maximization (under the full model).

References

Fox, John. 1997. Applied Regression Analysis, Linear Models, and Related Methods. sage publications, Inc.