12.4 Panel Data

Detail notes in R can be found here

Follows an individual over T time periods.

Panel data structure is like having n samples of time series data

Characteristics

  • Information both across individuals and over time (cross-sectional and time-series)

  • N individuals and T time periods

  • Data can be either

    • Balanced: all individuals are observed in all time periods
    • Unbalanced: all individuals are not observed in all time periods.

  • Assume correlation (clustering) over time for a given individual, with independence over individuals.

Types

  • Short panel: many individuals and few time periods.
  • Long panel: many time periods and few individuals
  • Both: many time periods and many individuals

Time Trends and Time Effects

  • Nonlinear
  • Seasonality
  • Discontinuous shocks

Regressors

  • Time-invariant regressors \(x_{it}=x_i\) for all t (e.g., gender, race, education) have zero within variation
  • Individual-invariant regressors \(x_{it}=x_{t}\) for all i (e.g., time trend, economy trends) have zero between variation

Variation for the dependent variable and regressors

  • Overall variation: variation over time and individuals.
  • Between variation: variation between individuals
  • Within variation: variation within individuals (over time).
Estimate Formula
Individual mean \(\bar{x_i}= \frac{1}{T} \sum_{t}x_{it}\)
Overall mean \(\bar{x}=\frac{1}{NT} \sum_{i} \sum_t x_{it}\)
Overall Variance \(s _O^2 = \frac{1}{NT-1} \sum_i \sum_t (x_{it} - \bar{x})^2\)
Between variance \(s_B^2 = \frac{1}{N-1} \sum_i (\bar{x_i} -\bar{x})^2\)
Within variance \(s_W^2= \frac{1}{NT-1} \sum_i \sum_t (x_{it} - \bar{x_i})^2 = \frac{1}{NT-1} \sum_i \sum_t (x_{it} - \bar{x_i} +\bar{x})^2\)

Note: \(s_O^2 \approx s_B^2 + s_W^2\)

Since we have n observation for each time period t, we can control for each time effect separately by including time dummies (time effects)

\[ y_{it}=\mathbf{x_{it}\beta} + d_1\delta_1+...+d_{T-1}\delta_{T-1} + \epsilon_{it} \]

Note: we cannot use these many time dummies in time series data because in time series data, our n is 1. Hence, there is no variation, and sometimes not enough data compared to variables to estimate coefficients.

Unobserved Effects Model Similar to group clustering, assume that there is a random effect that captures differences across individuals but is constant in time.

\[ y_it=\mathbf{x_{it}\beta} + d_1\delta_1+...+d_{T-1}\delta_{T-1} + c_i + u_{it} \]

where

  • \(c_i + u_{it} = \epsilon_{it}\)
  • \(c_i\) unobserved individual heterogeneity (effect)
  • \(u_{it}\) idiosyncratic shock
  • \(\epsilon_{it}\) unobserved error term.

12.4.1 Pooled OLS Estimator

If \(c_i\) is uncorrelated with \(x_{it}\)

\[ E(\mathbf{x_{it}'}(c_i+u_{it})) = 0 \]

then A3a still holds. And we have Pooled OLS consistent.

If A4 does not hold, OLS is still consistent, but not efficient, and we need cluster robust SE.

Sufficient for A3a to hold, we need

  • Exogeneity for \(u_{it}\) A3a (contemporaneous exogeneity): \(E(\mathbf{x_{it}'}u_{it})=0\) time varying error
  • Random Effect Assumption (time constant error): \(E(\mathbf{x_{it}'}c_{i})=0\)

Pooled OLS will give you consistent coefficient estimates under A1, A2, A3a (for both \(u_{it}\) and RE assumption), and A5 (randomly sampling across i).

12.4.2 Individual-specific effects model

  • If we believe that there is unobserved heterogeneity across individual (e.g., unobserved ability of an individual affects \(y\)), If the individual-specific effects are correlated with the regressors, then we have the Fixed Effects Estimator. and if they are not correlated we have the Random Effects Estimator.

12.4.2.1 Random Effects Estimator

Random Effects estimator is the Feasible GLS estimator that assumes \(u_{it}\) is serially uncorrelated and homoskedastic

  • Under A1, A2, A3a (for both \(u_{it}\) and RE assumption) and A5 (randomly sampling across i), RE estimator is consistent.

    • If A4 holds for \(u_{it}\), RE is the most efficient estimator
    • If A4 fails to hold (may be heteroskedasticity across i, and serial correlation over t), then RE is not the most efficient, but still more efficient than pooled OLS.

12.4.2.2 Fixed Effects Estimator

also known as Within Estimator uses within variation (over time)

If the RE assumption is not hold (\(E(\mathbf{x_{it}'}c_i) \neq 0\)), then A3a does not hold (\(E(\mathbf{x_{it}'}\epsilon_i) \neq 0\)).

Hence, the OLS and RE are inconsistent/biased (because of omitted variable bias)

However, FE can only fix bias due to time-invariant factors (both observables and unobservables) correlated with treatment (not time-variant factors that correlated with the treatment).

The traditional FE technique is flawed when lagged dependent variables are included in the model. (Nickell 1981) (Narayanan and Nair 2013)

With measurement error in the independent, FE will exacerbate the errors-in-the-variables bias.

12.4.2.2.1 Demean Approach

To deal with violation in \(c_i\), we have

\[ y_{it}= \mathbf{x_{it} \beta} + c_i + u_{it} \]

\[ \bar{y_i}=\bar{\mathbf{x_i}} \beta + c_i + \bar{u_i} \]

where the second equation is the time averaged equation

using within transformation, we have

\[ y_{it} - \bar{y_i} = \mathbf{(x_{it} - \bar{x_i})}\beta + u_{it} - \bar{u_i} \]

because \(c_i\) is time constant.

The Fixed Effects estimator uses POLS on the transformed equation

\[ y_{it} - \bar{y_i} = \mathbf{(x_{it} - \bar{x_i})} \beta + d_1\delta_1 + ... + d_{T-2}\delta_{T-2} + u_{it} - \bar{u_i} \]

  • we need A3 (strict exogeneity) (\(E((\mathbf{x_{it}-\bar{x_i}})'(u_{it}-\bar{u_i})=0\)) to have FE consistent.

  • Variables that are time constant will be absorbed into \(c_i\). Hence we cannot make inference on time constant independent variables.

    • If you are interested in the effects of time-invariant variables, you could consider the OLS or between estimator

  • It’s recommended that you should still use cluster robust standard errors.

12.4.2.2.2 Dummy Approach

Equivalent to the within transformation (i.e., mathematically equivalent to Demean Approach), we can have the fixed effect estimator be the same with the dummy regression

\[ y_{it} = x_{it}\beta + d_1\delta_1 + ... + d_{T-2}\delta_{T-2} + c_1\gamma_1 + ... + c_{n-1}\gamma_{n-1} + u_{it} \]

where

\[ c_i = \begin{cases} 1 &\text{if observation is i} \\ 0 &\text{otherwise} \\ \end{cases} \]

  • The standard error is incorrectly calculated.
  • the FE within transformation is controlling for any difference across individual which is allowed to correlated with observables.
12.4.2.2.3 First-difference Approach

Economists typically use this approach

\[ y_{it} - y_{i (t-1)} = (\mathbf{x}_{it} - \mathbf{x}_{i(t-1)}) \beta + + (u_{it} - u_{i(t-1)}) \]

12.4.2.2.4 Fixed Effects Summary

  • The three approaches are almost equivalent.

  • Since fixed effect is a within estimator, only status changes can contribute to \(\beta\) variation.

    • Hence, with a small number of changes then the standard error for \(\beta\) will explode

  • Status changes mean subjects change from (1) control to treatment group or (2) treatment to control group. Those who have status change, we call them switchers.

    • Treatment effect is typically non-directional.

    • You can give a parameter for the direction if needed.

  • Issues:

    • You could have fundamental difference between switchers and non-switchers. Even though we can’t definitive test this, but providing descriptive statistics on switchers and non-switchers can give us confidence in our conclusion.

    • Because fixed effects focus on bias reduction, you might have larger variance (typically, with fixed effects you will have less df)

  • If the true model is random effect, economists typically don’t care, especially when \(c_i\) is the random effect and \(c_i \perp x_{it}\) (because RE assumption is that it is unrelated to \(x_{it}\)). The reason why economists don’t care is because RE wouldn’t correct bias, it only improves efficiency over OLS.

  • You can estimate FE for different units (not just individuals).

  • FE removes bias from time invariant factors but not without costs because it uses within variation, which imposes strict exogeneity assumption on \(u_{it}\): \(E[(x_{it} - \bar{x}_{i})(u_{it} - \bar{u}_{it})]=0\)

Recall

\[ Y_{it} = \beta_0 + X_{it}\beta_1 + \alpha_i + u_{it} \]

where \(\epsilon_{it} = \alpha_i + u_{it}\)

\[ \hat{\sigma}^2_\epsilon = \frac{SSR_{OLS}}{NT - K} \]

\[ \hat{\sigma}^2_u = \frac{SSR_{FE}}{NT - (N+K)} = \frac{SSR_{FE}}{N(T-1)-K} \]

It’s ambiguous whether your variance of error changes up or down because SSR can increase while the denominator decreases.

FE can be unbiased, but not consistent (i.e., not converging to the true effect)

12.4.2.2.5 FE Examples
12.4.2.2.6 Blau (1999)

  • Intergenerational mobility

  • If we transfer resources to low income family, can we generate upward mobility (increase ability)?

Mechanisms for intergenerational mobility

  1. Genetic (policy can’t affect) (i.e., ability endowment)
  2. Environmental indirect
  3. Environmental direct

\[ \frac{\% \Delta \text{Human capital}}{\% \Delta \text{income}} \]

  1. Financial transfer

Income measures:

  1. Total household income
  2. Wage income
  3. Non-wage income
  4. Annual versus permanent income

Core control variables:

Bad controls are those jointly determined with dependent variable

Control by mother = choice by mother

Uncontrolled by mothers:

  • mother race

  • location of birth

  • education of parents

  • household structure at age 14

\[ Y_{ijt} = X_{jt} \beta_i + I_{jt} \alpha_i + \epsilon_{ijt} \]

where

  • \(i\) = test

  • \(j\) = individual (child)

  • \(t\) = time

Grandmother’s model

Since child is nested within mother and mother nested within grandmother, the fixed effect of child is included in the fixed effect of mother, which is included in the fixed-effect of grandmother

\[ Y_{ijgmt} = X_{it} \beta_{i} + I_{jt} \alpha_i + \gamma_g + u_{ijgmt} \]

where

  • \(i\) = test, \(j\) = kid, \(m\) = mother, \(g\) = grandmother

  • where \(\gamma_g\) includes \(\gamma_m\) includes \(\gamma_j\)

Grandma fixed-effect

Pros:

  • control for some genetics + fixed characteristics of how mother are raised

  • can estimate effect of parameter income

Con:

  • Might not be a sufficient control

Common to cluster a the fixed-effect level (common correlated component)

Fixed effect exaggerates attenuation bias

Error rate on survey can help you fix this (plug in the number only , but not the uncertainty associated with that number).

12.4.2.2.7 Babcock (2010)

\[ T_{ijct} = \alpha_0 + S_{jct} \alpha_1 + X_{ijct} \alpha_2 + u_{ijct} \]

where

  • \(S_{jct}\) is the average class expectation

  • \(X_{ijct}\alpha_2\) is the individual characteristics

  • \(i\) student

  • \(j\) instructor

  • \(c\) course

  • \(t\) time

\[ T_{ijct} = \beta_0+ S_{jct} \beta_1+ X_{ijct} \beta_2 +\mu_{jc} + \epsilon_{ijct} \]

where \(\mu_{jc}\) is instructor by course fixed effect (unique id), which is different from \((\theta_j + \delta_c)\)

  1. Decrease course shopping because conditioned on available information (\(\mu_{jc}\)) (class grade and instructor’s info).
  2. Grade expectation change even though class materials stay the same

Identification strategy is

  • Under (fixed) time-varying factor that could bias my coefficient (simultaneity)

\[ Y_{ijt} = X_{it} \beta_1 + \text{Teacher Experience}_{jt} \beta_2 + \text{Teacher education}_{jt} \beta_3 + \text{Teacher score}_{it}\beta_4 + \dots + \epsilon_{ijt} \]

Drop teacher characteristics, and include teacher dummy effect

\[ Y_{ijt} = X_{it} \alpha + \Gamma_{it} \theta_j + u_{ijt} \]

where \(\alpha\) is the within teacher (conditional on teacher fixed effect) and \(j = 1 \to (J-1)\)

Nuisance in the sense that we don’t about the interpretation of \(\alpha\)

The least we can say about \(\theta_j\) is the teacher effect conditional on student test score.

\[ Y_{ijt} = X_{it} \gamma + \epsilon_{ijt} \]

\(\gamma\) is between within (unconditional) and \(e_{ijt}\) is the prediction error

\[ e_{ijt} = T_{it} \delta_j + \tilde{e}_{ijt} \]

where \(\delta_j\) is the mean for each group

\[ Y_{ijkt} = Y_{ijkt-1} + X_{it} \beta + T_{it} \tau_j + (W_i + P_k + \epsilon_{ijkt}) \]

where

  • \(Y_{ijkt-1}\) = lag control

  • \(\tau_j\) = teacher fixed time

  • \(W_i\) is the student fixed effect

  • \(P_k\) is the school fixed effect

  • \(u_{ijkt} = W_i + P_k + \epsilon_{ijkt}\)

And we worry about selection on class and school

Bias in \(\tau\) (for 1 teacher) is

\[ \frac{1}{N_j} \sum_{i = 1}^N (W_i + P_k + \epsilon_{ijkt}) \]

where \(N_j\) = the number of student in class with teacher \(j\)

then we can \(P_k + \frac{1}{N_j} \sum_{i = 1}^{N_j} (W_i + \epsilon_{ijkt})\)

Shocks from small class can bias \(\tau\)

\[ \frac{1}{N_j} \sum_{i = 1}^{N_j} \epsilon_{ijkt} \neq 0 \]

which will inflate the teacher fixed effect

Even if we create random teacher fixed effect and put it in the model, it still contains bias mentioned above which can still \(\tau\) (but we do not know the way it will affect - whether more positive or negative).

If teachers switch schools, then we can estimate both teacher and school fixed effect (mobility web thin vs. thick)

Mobility web refers to the web of switchers (i.e., from one status to another).

\[ Y_{ijkt} = Y_{ijk(t-1)} \alpha + X_{it}\beta + T_{it} \tau + P_k + \epsilon_{ijkt} \]

If we demean (fixed-effect), \(\tau\) (teacher fixed effect) will go away

If you want to examine teacher fixed effect, we have to include teacher fixed effect

Control for school, the article argues that there is no selection bias

For \(\frac{1}{N_j} \sum_{i =1}^{N_j} \epsilon_{ijkt}\) (teacher-level average residuals), \(var(\tau)\) does not change with \(N_j\) (Figure 2 in the paper). In words, the quality of teachers is not a function of the number of students

If \(var(\tau) =0\) it means that teacher quality does not matter

Spin-off of Measurement Error: Sampling error or estimation error

\[ \hat{\tau}_j = \tau_j + \lambda_j \]

\[ var(\hat{\tau}) = var(\tau + \lambda) \]

Assume \(cov(\tau_j, \lambda_j)=0\) (reasonable) In words, your randomness in getting children does not correlation with teacher quality.

Hence,

\[ \begin{aligned} var(\hat{\tau}) &= var(\tau) + var(\lambda) \\ var(\tau) &= var(\hat{\tau}) - var(\lambda) \\ \end{aligned} \]

We have \(var(\hat{\tau})\) and we need to estimate \(var(\lambda)\)

\[ var(\lambda) = \frac{1}{J} \sum_{j=1}^J \hat{\sigma}^2_j \] where \(\hat{\sigma}^2_j\) is the squared standard error of the teacher \(j\) (a function of \(n\))

Hence,

\[ \frac{var(\tau)}{var(\hat{\tau})} = \text{reliability} = \text{true variance signal} \] also known as how much noise in \(\hat{\tau}\) and

\[ 1 - \frac{var(\tau)}{var(\hat{\tau})} = \text{noise} \]

Even in cases where the true relationship is that \(\tau\) is a function of \(N_j\), then our recovery method for \(\lambda\) is still not affected

To examine our assumption

\[ \hat{\tau}_j = \beta_0 + X_j \beta_1 + \epsilon_j \]

Regressing teacher fixed-effect on teacher characteristics should give us \(R^2\) close to 0, because teacher characteristics cannot predict sampling error (\(\hat{\tau}\) contain sampling error)

12.4.3 Tests for Assumptions

We typically don’t test heteroskedasticity because we will use robust covariance matrix estimation anyway.

Dataset

library("plm")
data("EmplUK", package="plm")
data("Produc", package="plm")
data("Grunfeld", package="plm")
data("Wages", package="plm")

12.4.3.1 Poolability

also known as an F test of stability (or Chow test) for the coefficients

\(H_0\): All individuals have the same coefficients (i.e., equal coefficients for all individuals).

\(H_a\) Different individuals have different coefficients.

Notes:

  • Under a within (i.e., fixed) model, different intercepts for each individual are assumed
  • Under random model, same intercept is assumed
library(plm)
plm::pooltest(inv~value+capital, data=Grunfeld, model="within")
#> 
#>  F statistic
#> 
#> data:  inv ~ value + capital
#> F = 5.7805, df1 = 18, df2 = 170, p-value = 1.219e-10
#> alternative hypothesis: unstability

Hence, we reject the null hypothesis that coefficients are stable. Then, we should use the random model.

12.4.3.2 Individual and time effects

use the Lagrange multiplier test to test the presence of individual or time or both (i.e., individual and time).

Types:

pFtest(inv~value+capital, data=Grunfeld, effect="twoways")
#> 
#>  F test for twoways effects
#> 
#> data:  inv ~ value + capital
#> F = 17.403, df1 = 28, df2 = 169, p-value < 2.2e-16
#> alternative hypothesis: significant effects
pFtest(inv~value+capital, data=Grunfeld, effect="individual")
#> 
#>  F test for individual effects
#> 
#> data:  inv ~ value + capital
#> F = 49.177, df1 = 9, df2 = 188, p-value < 2.2e-16
#> alternative hypothesis: significant effects
pFtest(inv~value+capital, data=Grunfeld, effect="time")
#> 
#>  F test for time effects
#> 
#> data:  inv ~ value + capital
#> F = 0.23451, df1 = 19, df2 = 178, p-value = 0.9997
#> alternative hypothesis: significant effects

12.4.3.3 Cross-sectional dependence/contemporaneous correlation

  • Null hypothesis: residuals across entities are not correlated.
12.4.3.3.1 Global cross-sectional dependence
pcdtest(inv~value+capital, data=Grunfeld, model="within")
#> 
#>  Pesaran CD test for cross-sectional dependence in panels
#> 
#> data:  inv ~ value + capital
#> z = 4.6612, p-value = 3.144e-06
#> alternative hypothesis: cross-sectional dependence
12.4.3.3.2 Local cross-sectional dependence

use the same command, but supply matrix w to the argument.

pcdtest(inv~value+capital, data=Grunfeld, model="within")
#> 
#>  Pesaran CD test for cross-sectional dependence in panels
#> 
#> data:  inv ~ value + capital
#> z = 4.6612, p-value = 3.144e-06
#> alternative hypothesis: cross-sectional dependence

12.4.3.4 Serial Correlation

  • Null hypothesis: there is no serial correlation

  • usually seen in macro panels with long time series (large N and T), not seen in micro panels (small T and large N)

  • Serial correlation can arise from individual effects(i.e., time-invariant error component), or idiosyncratic error terms (e..g, in the case of AR(1) process). But typically, when we refer to serial correlation, we refer to the second one.

  • Can be

    • marginal test: only 1 of the two above dependence (but can be biased towards rejection)

    • joint test: both dependencies (but don’t know which one is causing the problem)

    • conditional test: assume you correctly specify one dependence structure, test whether the other departure is present.

12.4.3.4.1 Unobserved effect test

  • semi-parametric test (the test statistic \(W \dot{\sim} N\) regardless of the distribution of the errors) with \(H_0: \sigma^2_\mu = 0\) (i.e., no unobserved effects in the residuals), favors pooled OLS.

    • Under the null, covariance matrix of the residuals = its diagonal (off-diagonal = 0)

  • It is robust against both unobserved effects that are constant within every group, and any kind of serial correlation.

pwtest(log(gsp) ~ log(pcap) + log(pc) + log(emp) + unemp, data = Produc)
#> 
#>  Wooldridge's test for unobserved individual effects
#> 
#> data:  formula
#> z = 3.9383, p-value = 8.207e-05
#> alternative hypothesis: unobserved effect

Here, we reject the null hypothesis that the no unobserved effects in the residuals. Hence, we will exclude using pooled OLS.

12.4.3.4.2 Locally robust tests for random effects and serial correlation
  • A joint LM test for random effects and serial correlation assuming normality and homoskedasticity of the idiosyncratic errors [Baltagi and Li (1991)](Baltagi and Li 1995)
pbsytest(log(gsp) ~ log(pcap) + log(pc) + log(emp) + unemp,
         data = Produc,
         test = "j")
#> 
#>  Baltagi and Li AR-RE joint test
#> 
#> data:  formula
#> chisq = 4187.6, df = 2, p-value < 2.2e-16
#> alternative hypothesis: AR(1) errors or random effects

Here, we reject the null hypothesis that there is no presence of serial correlation, and random effects. But we still do not know whether it is because of serial correlation, of random effects or of both

To know the departure from the null assumption, we can use Bera, Sosa-Escudero, and Yoon (2001)’s test for first-order serial correlation or random effects (both under normality and homoskedasticity assumption of the error).

BSY for serial correlation

pbsytest(log(gsp) ~ log(pcap) + log(pc) + log(emp) + unemp,
         data = Produc)
#> 
#>  Bera, Sosa-Escudero and Yoon locally robust test
#> 
#> data:  formula
#> chisq = 52.636, df = 1, p-value = 4.015e-13
#> alternative hypothesis: AR(1) errors sub random effects

BSY for random effects

pbsytest(log(gsp)~log(pcap)+log(pc)+log(emp)+unemp, 
         data=Produc, 
         test="re")
#> 
#>  Bera, Sosa-Escudero and Yoon locally robust test (one-sided)
#> 
#> data:  formula
#> z = 57.914, p-value < 2.2e-16
#> alternative hypothesis: random effects sub AR(1) errors

Since BSY is only locally robust, if you “know” there is no serial correlation, then this test is based on LM test is more superior:

plmtest(inv ~ value + capital, data = Grunfeld, 
        type = "honda")
#> 
#>  Lagrange Multiplier Test - (Honda)
#> 
#> data:  inv ~ value + capital
#> normal = 28.252, p-value < 2.2e-16
#> alternative hypothesis: significant effects

On the other hand, if you know there is no random effects, to test for serial correlation, use (Breusch 1978)-(Godfrey 1978)’s test

lmtest::bgtest()

If you “know” there are random effects, use (Baltagi and Li 1995)’s. to test for serial correlation in both AR(1) and MA(1) processes.

\(H_0\): Uncorrelated errors.

Note:

  • one-sided only has power against positive serial correlation.
  • applicable to only balanced panels.
pbltest(
    log(gsp) ~ log(pcap) + log(pc) + log(emp) + unemp,
    data = Produc,
    alternative = "onesided"
)
#> 
#>  Baltagi and Li one-sided LM test
#> 
#> data:  log(gsp) ~ log(pcap) + log(pc) + log(emp) + unemp
#> z = 21.69, p-value < 2.2e-16
#> alternative hypothesis: AR(1)/MA(1) errors in RE panel model

General serial correlation tests

  • applicable to random effects model, OLS, and FE (with large T, also known as long panel).
  • can also test higher-order serial correlation
plm::pbgtest(plm::plm(inv ~ value + capital,
                      data = Grunfeld,
                      model = "within"),
             order = 2)
#> 
#>  Breusch-Godfrey/Wooldridge test for serial correlation in panel models
#> 
#> data:  inv ~ value + capital
#> chisq = 42.587, df = 2, p-value = 5.655e-10
#> alternative hypothesis: serial correlation in idiosyncratic errors

in the case of short panels (small T and large n), we can use

pwartest(log(emp) ~ log(wage) + log(capital), data=EmplUK)
#> 
#>  Wooldridge's test for serial correlation in FE panels
#> 
#> data:  plm.model
#> F = 312.3, df1 = 1, df2 = 889, p-value < 2.2e-16
#> alternative hypothesis: serial correlation

12.4.3.5 Unit roots/stationarity

  • Dickey-Fuller test for stochastic trends.
  • Null hypothesis: the series is non-stationary (unit root)
  • You would want your test to be less than the critical value (p<.5) so that there is evidence there is not unit roots.

12.4.3.6 Heteroskedasticity

  • Breusch-Pagan test

  • Null hypothesis: the data is homoskedastic

  • If there is evidence for heteroskedasticity, robust covariance matrix is advised.

  • To control for heteroskedasticity: Robust covariance matrix estimation (Sandwich estimator)

    • “white1” - for general heteroskedasticity but no serial correlation (check serial correlation first). Recommended for random effects.
    • “white2” - is “white1” restricted to a common variance within groups. Recommended for random effects.
    • “arellano” - both heteroskedasticity and serial correlation. Recommended for fixed effects

12.4.4 Model Selection

12.4.4.1 POLS vs. RE

The continuum between RE (used FGLS which more assumption ) and POLS check back on the section of FGLS

Breusch-Pagan LM test

  • Test for the random effect model based on the OLS residual
  • Null hypothesis: variances across entities is zero. In another word, no panel effect.
  • If the test is significant, RE is preferable compared to POLS

12.4.4.2 FE vs. RE

  • RE does not require strict exogeneity for consistency (feedback effect between residual and covariates)
Hypothesis If true
\(H_0: Cov(c_i,\mathbf{x_{it}})=0\) \(\hat{\beta}_{RE}\) is consistent and efficient, while \(\hat{\beta}_{FE}\) is consistent
\(H_0: Cov(c_i,\mathbf{x_{it}}) \neq 0\) \(\hat{\beta}_{RE}\) is inconsistent, while \(\hat{\beta}_{FE}\) is consistent

Hausman Test

For the Hausman test to run, you need to assume that

  • strict exogeneity hold
  • A4 to hold for \(u_{it}\)

Then,

  • Hausman test statistic: \(H=(\hat{\beta}_{RE}-\hat{\beta}_{FE})'(V(\hat{\beta}_{RE})- V(\hat{\beta}_{FE}))(\hat{\beta}_{RE}-\hat{\beta}_{FE}) \sim \chi_{n(X)}^2\) where \(n(X)\) is the number of parameters for the time-varying regressors.
  • A low p-value means that we would reject the null hypothesis and prefer FE
  • A high p-value means that we would not reject the null hypothesis and consider RE estimator.
gw <- plm(inv ~ value + capital, data = Grunfeld, model = "within")
gr <- plm(inv ~ value + capital, data = Grunfeld, model = "random")
phtest(gw, gr)
#> 
#>  Hausman Test
#> 
#> data:  inv ~ value + capital
#> chisq = 2.3304, df = 2, p-value = 0.3119
#> alternative hypothesis: one model is inconsistent
  • Violation Estimator
  • Basic Estimator
  • Instrumental variable Estimator
  • Variable Coefficients estimator
  • Generalized Method of Moments estimator
  • General FGLS estimator
  • Means groups estimator
  • CCEMG
  • Estimator for limited dependent variables

12.4.5 Summary

  • All three estimators (POLS, RE, FE) require A1, A2, A5 (for individuals) to be consistent. Additionally,

  • POLS is consistent under A3a(for \(u_{it}\)): \(E(\mathbf{x}_{it}'u_{it})=0\), and RE Assumption \(E(\mathbf{x}_{it}'c_{i})=0\)

    • If A4 does not hold, use cluster robust SE but POLS is not efficient

  • RE is consistent under A3a(for \(u_{it}\)): \(E(\mathbf{x}_{it}'u_{it})=0\), and RE Assumption \(E(\mathbf{x}_{it}'c_{i})=0\)

    • If A4 (for \(u_{it}\)) holds then usual SE are valid and RE is most efficient
    • If A4 (for \(u_{it}\)) does not hold, use cluster robust SE ,and RE is no longer most efficient (but still more efficient than POLS)

  • FE is consistent under A3 \(E((\mathbf{x}_{it}-\bar{\mathbf{x}}_{it})'(u_{it} -\bar{u}_{it}))=0\)

    • Cannot estimate effects of time constant variables
    • A4 generally does not hold for \(u_{it} -\bar{u}_{it}\) so cluster robust SE are needed

Note: A5 for individual (not for time dimension) implies that you have A5a for the entire data set.

Estimator / True Model POLS RE FE
POLS Consistent Consistent Inconsistent
FE Consistent Consistent Consistent
RE Consistent Consistent Inconsistent

Based on table provided by Ani Katchova

12.4.6 Application

12.4.6.1 plm package

Recommended application of plm can be found here and here by Yves Croissant

#install.packages("plm")
library("plm")

library(foreign)
Panel <- read.dta("http://dss.princeton.edu/training/Panel101.dta")

attach(Panel)
Y <- cbind(y)
X <- cbind(x1, x2, x3)

# Set data as panel data
pdata <- pdata.frame(Panel, index = c("country", "year"))

# Pooled OLS estimator
pooling <- plm(Y ~ X, data = pdata, model = "pooling")
summary(pooling)

# Between estimator
between <- plm(Y ~ X, data = pdata, model = "between")
summary(between)

# First differences estimator
firstdiff <- plm(Y ~ X, data = pdata, model = "fd")
summary(firstdiff)

# Fixed effects or within estimator
fixed <- plm(Y ~ X, data = pdata, model = "within")
summary(fixed)

# Random effects estimator
random <- plm(Y ~ X, data = pdata, model = "random")
summary(random)

# LM test for random effects versus OLS
# Accept Null, then OLS, Reject Null then RE
plmtest(pooling, effect = "individual", type = c("bp")) 
# other type: "honda", "kw"," "ghm"; other effect : "time" "twoways"


# B-P/LM and Pesaran CD (cross-sectional dependence) test
# Breusch and Pagan's original LM statistic
pcdtest(fixed, test = c("lm")) 
# Pesaran's CD statistic
pcdtest(fixed, test = c("cd")) 

# Serial Correlation
pbgtest(fixed)

# stationary
library("tseries")
adf.test(pdata$y, k = 2)

# LM test for fixed effects versus OLS
pFtest(fixed, pooling)

# Hausman test for fixed versus random effects model
phtest(random, fixed)

# Breusch-Pagan heteroskedasticity
library(lmtest)
bptest(y ~ x1 + factor(country), data = pdata)

# If there is presence of heteroskedasticity
## For RE model
coeftest(random) #orginal coef

# Heteroskedasticity consistent coefficients
coeftest(random, vcovHC) 

t(sapply(c("HC0", "HC1", "HC2", "HC3", "HC4"), function(x)
    sqrt(diag(
        vcovHC(random, type = x)
    )))) #show HC SE of the coef
# HC0 - heteroskedasticity consistent. The default.
# HC1,HC2, HC3 – Recommended for small samples. 
# HC3 gives less weight to influential observations.
# HC4 - small samples with influential observations
# HAC - heteroskedasticity and autocorrelation consistent

## For FE model
coeftest(fixed) # Original coefficients
coeftest(fixed, vcovHC) # Heteroskedasticity consistent coefficients

# Heteroskedasticity consistent coefficients (Arellano)
coeftest(fixed, vcovHC(fixed, method = "arellano")) 

t(sapply(c("HC0", "HC1", "HC2", "HC3", "HC4"), function(x)
    sqrt(diag(
        vcovHC(fixed, type = x)
    )))) #show HC SE of the coef

Advanced

Other methods to estimate the random model:

Other effects:

  • Individual effects: default
  • Time effects: "time"
  • Individual and time effects: "twoways"

Note: no random two-ways effect model for random.method = "nerlove"

amemiya <-
    plm(
        Y ~ X,
        data = pdata,
        model = "random",
        random.method = "amemiya",
        effect = "twoways"
    )

To call the estimation of the variance of the error components

ercomp(Y ~ X,
       data = pdata,
       method = "amemiya",
       effect = "twoways")

Check for the unbalancedness. Closer to 1 indicates balanced data (Ahrens and Pincus 1981)

punbalancedness(random)

Instrumental variable

instr <-
    plm(
        Y ~ X | X_ins,
        data = pdata,
        random.method = "ht",
        model = "random",
        inst.method = "baltagi"
    )
12.4.6.1.1 Other Estimators
12.4.6.1.1.1 Variable Coefficients Model
fixed_pvcm  <- pvcm(Y ~ X, data = pdata, model = "within")
random_pvcm <- pvcm(Y ~ X, data = pdata, model = "random")

More details can be found here

12.4.6.1.1.2 Generalized Method of Moments Estimator

Typically use in dynamic models. Example is from plm package

z2 <- pgmm(
    log(emp) ~ lag(log(emp), 1) + lag(log(wage), 0:1) +
        lag(log(capital), 0:1) | lag(log(emp), 2:99) +
        lag(log(wage), 2:99) + lag(log(capital), 2:99),
    data = EmplUK,
    effect = "twoways",
    model = "onestep",
    transformation = "ld"
)
summary(z2, robust = TRUE)
12.4.6.1.1.3 General Feasible Generalized Least Squares Models

Assume there is no cross-sectional correlation Robust against intragroup heteroskedasticity and serial correlation. Suited when n is much larger than T (long panel) However, inefficient under group-wise heteorskedasticity.

# Random Effects
zz <-
    pggls(log(emp) ~ log(wage) + log(capital),
          data = EmplUK,
          model = "pooling")

# Fixed
zz <-
    pggls(log(emp) ~ log(wage) + log(capital),
          data = EmplUK,
          model = "within")

12.4.6.2 fixest package

Available functions

  • feols: linear models

  • feglm: generalized linear models

  • femlm: maximum likelihood estimation

  • feNmlm: non-linear in RHS parameters

  • fepois: Poisson fixed-effect

  • fenegbin: negative binomial fixed-effect

Notes

  • can only work for fixest object

Examples by the package’s authors

library(fixest)
data(airquality)

# Setting a dictionary
setFixest_dict(
    c(
        Ozone   = "Ozone (ppb)",
        Solar.R = "Solar Radiation (Langleys)",
        Wind    = "Wind Speed (mph)",
        Temp    = "Temperature"
    )
)


# On multiple estimations: see the dedicated vignette
est = feols(
    Ozone ~ Solar.R + sw0(Wind + Temp) | csw(Month, Day),
    data = airquality,
    cluster = ~ Day
)

etable(est)
#>                                         est.1              est.2
#> Dependent Var.:                   Ozone (ppb)        Ozone (ppb)
#>                                                                 
#> Solar Radiation (Langleys) 0.1148*** (0.0234)   0.0522* (0.0202)
#> Wind Speed (mph)                              -3.109*** (0.7986)
#> Temperature                                    1.875*** (0.3671)
#> Fixed-Effects:             ------------------ ------------------
#> Month                                     Yes                Yes
#> Day                                        No                 No
#> __________________________ __________________ __________________
#> S.E.: Clustered                       by: Day            by: Day
#> Observations                              111                111
#> R2                                    0.31974            0.63686
#> Within R2                             0.12245            0.53154
#> 
#>                                        est.3              est.4
#> Dependent Var.:                  Ozone (ppb)        Ozone (ppb)
#>                                                                
#> Solar Radiation (Langleys) 0.1078** (0.0329)   0.0509* (0.0236)
#> Wind Speed (mph)                             -3.289*** (0.7777)
#> Temperature                                   2.052*** (0.2415)
#> Fixed-Effects:             ----------------- ------------------
#> Month                                    Yes                Yes
#> Day                                      Yes                Yes
#> __________________________ _________________ __________________
#> S.E.: Clustered                      by: Day            by: Day
#> Observations                             111                111
#> R2                                   0.58018            0.81604
#> Within R2                            0.12074            0.61471
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

# in latex
etable(est, tex = T)
#> \begingroup
#> \centering
#> \begin{tabular}{lcccc}
#>    \tabularnewline \midrule \midrule
#>    Dependent Variable: & \multicolumn{4}{c}{Ozone (ppb)}\\
#>    Model:                     & (1)            & (2)            & (3)            & (4)\\  
#>    \midrule
#>    \emph{Variables}\\
#>    Solar Radiation (Langleys) & 0.1148$^{***}$ & 0.0522$^{**}$  & 0.1078$^{***}$ & 0.0509$^{**}$\\   
#>                               & (0.0234)       & (0.0202)       & (0.0329)       & (0.0236)\\   
#>    Wind Speed (mph)           &                & -3.109$^{***}$ &                & -3.289$^{***}$\\   
#>                               &                & (0.7986)       &                & (0.7777)\\   
#>    Temperature                &                & 1.875$^{***}$  &                & 2.052$^{***}$\\   
#>                               &                & (0.3671)       &                & (0.2415)\\   
#>    \midrule
#>    \emph{Fixed-effects}\\
#>    Month                      & Yes            & Yes            & Yes            & Yes\\  
#>    Day                        &                &                & Yes            & Yes\\  
#>    \midrule
#>    \emph{Fit statistics}\\
#>    Observations               & 111            & 111            & 111            & 111\\  
#>    R$^2$                      & 0.31974        & 0.63686        & 0.58018        & 0.81604\\  
#>    Within R$^2$               & 0.12245        & 0.53154        & 0.12074        & 0.61471\\  
#>    \midrule \midrule
#>    \multicolumn{5}{l}{\emph{Clustered (Day) standard-errors in parentheses}}\\
#>    \multicolumn{5}{l}{\emph{Signif. Codes: ***: 0.01, **: 0.05, *: 0.1}}\\
#> \end{tabular}
#> \par\endgroup


# get the fixed-effects coefficients for 1 model
fixedEffects = fixef(est[[1]])
summary(fixedEffects)
#> Fixed_effects coefficients
#> Number of fixed-effects for variable Month is 5.
#>  Mean = 19.6 Variance = 272
#> 
#> COEFFICIENTS:
#>   Month:     5     6     7     8     9
#>          3.219 8.288 34.26 40.12 12.13

# see the fixed effects for one dimension
fixedEffects$Month
#>         5         6         7         8         9 
#>  3.218876  8.287899 34.260812 40.122257 12.130971

plot(fixedEffects)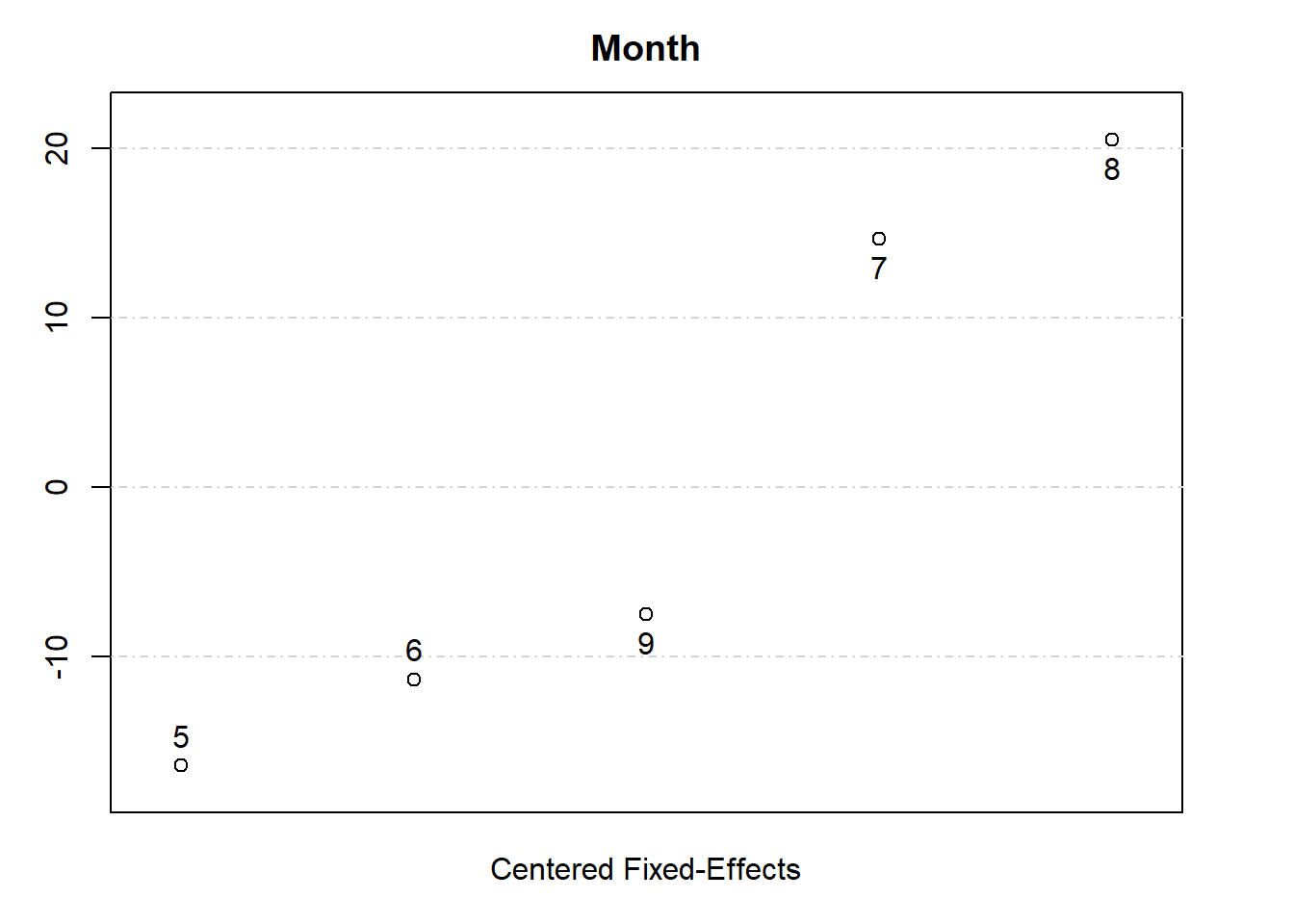

For multiple estimation

# set up
library(fixest)

# let R know the base dataset (the biggest/ultimate 
# dataset that includes everything in your analysis)
base = iris

# rename variables
names(base) = c("y1", "y2", "x1", "x2", "species")

res_multi = feols(
    c(y1, y2) ~ x1 + csw(x2, x2 ^ 2) |
        sw0(species),
    data = base,
    fsplit = ~ species,
    lean = TRUE,
    vcov = "hc1" # can also clustered at the fixed effect level
)
# it's recommended to use vcov at 
# estimation stage, not summary stage

summary(res_multi, "compact")
#>         sample   fixef lhs               rhs     (Intercept)                x1
#> 1  Full sample 1        y1 x1 + x2           4.19*** (0.104)  0.542*** (0.076)
#> 2  Full sample 1        y1 x1 + x2 + I(x2^2) 4.27*** (0.101)  0.719*** (0.082)
#> 3  Full sample 1        y2 x1 + x2           3.59*** (0.103) -0.257*** (0.066)
#> 4  Full sample 1        y2 x1 + x2 + I(x2^2) 3.68*** (0.097)    -0.030 (0.078)
#> 5  Full sample species  y1 x1 + x2                            0.906*** (0.076)
#> 6  Full sample species  y1 x1 + x2 + I(x2^2)                  0.900*** (0.077)
#> 7  Full sample species  y2 x1 + x2                              0.155* (0.073)
#> 8  Full sample species  y2 x1 + x2 + I(x2^2)                    0.148. (0.075)
#> 9  setosa      1        y1 x1 + x2           4.25*** (0.474)     0.399 (0.325)
#> 10 setosa      1        y1 x1 + x2 + I(x2^2) 4.00*** (0.504)     0.405 (0.325)
#> 11 setosa      1        y2 x1 + x2           2.89*** (0.416)     0.247 (0.305)
#> 12 setosa      1        y2 x1 + x2 + I(x2^2) 2.82*** (0.423)     0.248 (0.304)
#> 13 setosa      species  y1 x1 + x2                               0.399 (0.325)
#> 14 setosa      species  y1 x1 + x2 + I(x2^2)                     0.405 (0.325)
#> 15 setosa      species  y2 x1 + x2                               0.247 (0.305)
#> 16 setosa      species  y2 x1 + x2 + I(x2^2)                     0.248 (0.304)
#> 17 versicolor  1        y1 x1 + x2           2.38*** (0.423)  0.934*** (0.166)
#> 18 versicolor  1        y1 x1 + x2 + I(x2^2)   0.323 (1.44)   0.901*** (0.164)
#> 19 versicolor  1        y2 x1 + x2           1.25*** (0.275)     0.067 (0.095)
#> 20 versicolor  1        y2 x1 + x2 + I(x2^2)   0.097 (1.01)      0.048 (0.099)
#> 21 versicolor  species  y1 x1 + x2                            0.934*** (0.166)
#> 22 versicolor  species  y1 x1 + x2 + I(x2^2)                  0.901*** (0.164)
#> 23 versicolor  species  y2 x1 + x2                               0.067 (0.095)
#> 24 versicolor  species  y2 x1 + x2 + I(x2^2)                     0.048 (0.099)
#> 25 virginica   1        y1 x1 + x2             1.05. (0.539)  0.995*** (0.090)
#> 26 virginica   1        y1 x1 + x2 + I(x2^2)   -2.39 (2.04)   0.994*** (0.088)
#> 27 virginica   1        y2 x1 + x2             1.06. (0.572)     0.149 (0.107)
#> 28 virginica   1        y2 x1 + x2 + I(x2^2)    1.10 (1.76)      0.149 (0.108)
#> 29 virginica   species  y1 x1 + x2                            0.995*** (0.090)
#> 30 virginica   species  y1 x1 + x2 + I(x2^2)                  0.994*** (0.088)
#> 31 virginica   species  y2 x1 + x2                               0.149 (0.107)
#> 32 virginica   species  y2 x1 + x2 + I(x2^2)                     0.149 (0.108)
#>                  x2          I(x2^2)
#> 1   -0.320. (0.170)                 
#> 2  -1.52*** (0.307) 0.348*** (0.075)
#> 3    0.364* (0.142)                 
#> 4  -1.18*** (0.313) 0.446*** (0.074)
#> 5    -0.006 (0.163)                 
#> 6     0.290 (0.408)   -0.088 (0.117)
#> 7  0.623*** (0.114)                 
#> 8    0.951* (0.472)   -0.097 (0.125)
#> 9    0.712. (0.418)                 
#> 10    2.51. (1.47)     -2.91 (2.10) 
#> 11    0.702 (0.560)                 
#> 12     1.27 (2.39)    -0.911 (3.28) 
#> 13   0.712. (0.418)                 
#> 14    2.51. (1.47)     -2.91 (2.10) 
#> 15    0.702 (0.560)                 
#> 16     1.27 (2.39)    -0.911 (3.28) 
#> 17   -0.320 (0.364)                 
#> 18     3.01 (2.31)     -1.24 (0.841)
#> 19 0.929*** (0.244)                 
#> 20    2.80. (1.65)    -0.695 (0.583)
#> 21   -0.320 (0.364)                 
#> 22     3.01 (2.31)     -1.24 (0.841)
#> 23 0.929*** (0.244)                 
#> 24    2.80. (1.65)    -0.695 (0.583)
#> 25    0.007 (0.205)                 
#> 26    3.50. (2.09)    -0.870 (0.519)
#> 27 0.535*** (0.122)                 
#> 28    0.503 (1.56)     0.008 (0.388)
#> 29    0.007 (0.205)                 
#> 30    3.50. (2.09)    -0.870 (0.519)
#> 31 0.535*** (0.122)                 
#> 32    0.503 (1.56)     0.008 (0.388)

# call the first 3 estimated models only
etable(res_multi[1:3],
       
       # customize the headers
       headers = c("mod1", "mod2", "mod3")) 
#>                   res_multi[1:3].1   res_multi[1:3].2    res_multi[1:3].3
#>                               mod1               mod2                mod3
#> Dependent Var.:                 y1                 y1                  y2
#>                                                                          
#> Constant         4.191*** (0.1037)  4.266*** (0.1007)   3.587*** (0.1031)
#> x1              0.5418*** (0.0761) 0.7189*** (0.0815) -0.2571*** (0.0664)
#> x2               -0.3196. (0.1700) -1.522*** (0.3072)    0.3640* (0.1419)
#> x2 square                          0.3479*** (0.0748)                    
#> _______________ __________________ __________________ ___________________
#> S.E. type       Heteroskedas.-rob. Heteroskedas.-rob. Heteroskedast.-rob.
#> Observations                   150                150                 150
#> R2                         0.76626            0.79456             0.21310
#> Adj. R2                    0.76308            0.79034             0.20240
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
12.4.6.2.1 Multiple estimation (Left-hand side)
  • When you have multiple interested dependent variables
etable(feols(c(y1, y2) ~ x1 + x2, base))
#>                 feols(c(y1, y2)..1 feols(c(y1, y2) ..2
#> Dependent Var.:                 y1                  y2
#>                                                       
#> Constant         4.191*** (0.0970)   3.587*** (0.0937)
#> x1              0.5418*** (0.0693) -0.2571*** (0.0669)
#> x2               -0.3196* (0.1605)    0.3640* (0.1550)
#> _______________ __________________ ___________________
#> S.E. type                      IID                 IID
#> Observations                   150                 150
#> R2                         0.76626             0.21310
#> Adj. R2                    0.76308             0.20240
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

To input a list of dependent variable

depvars <- c("y1", "y2")

res <- lapply(depvars, function(var) {
    res <- feols(xpd(..lhs ~ x1 + x2, ..lhs = var), data = base)
    # summary(res)
})
etable(res)
#>                            model 1             model 2
#> Dependent Var.:                 y1                  y2
#>                                                       
#> Constant         4.191*** (0.0970)   3.587*** (0.0937)
#> x1              0.5418*** (0.0693) -0.2571*** (0.0669)
#> x2               -0.3196* (0.1605)    0.3640* (0.1550)
#> _______________ __________________ ___________________
#> S.E. type                      IID                 IID
#> Observations                   150                 150
#> R2                         0.76626             0.21310
#> Adj. R2                    0.76308             0.20240
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
12.4.6.2.2 Multiple estimation (Right-hand side)

Options to write the functions

  • sw (stepwise): sequentially analyze each elements

    • y ~ sw(x1, x2) will be estimated as y ~ x1 and y ~ x2

  • sw0 (stepwise 0): similar to sw but also estimate a model without the elements in the set first

    • y ~ sw(x1, x2) will be estimated as y ~ 1 and y ~ x1 and y ~ x2

  • csw (cumulative stepwise): sequentially add each element of the set to the formula

    • y ~ csw(x1, x2) will be estimated as y ~ x1 and y ~ x1 + x2

  • csw0 (cumulative stepwise 0): similar to csw but also estimate a model without the elements in the set first

    • y ~ csw(x1, x2) will be estimated as y~ 1 y ~ x1 and y ~ x1 + x2

  • mvsw (multiverse stepwise): all possible combination of the elements in the set (it will get large very quick).

    • mvsw(x1, x2, x3) will be sw0(x1, x2, x3, x1 + x2, x1 + x3, x2 + x3, x1 + x2 + x3)
12.4.6.2.3 Split sample estimation
etable(feols(y1 ~ x1 + x2, fsplit = ~ species, data = base))
#>                  feols(y1 ~ x1 +..1 feols(y1 ~ x1 ..2 feols(y1 ~ x1 +..3
#> Sample (species)        Full sample            setosa         versicolor
#> Dependent Var.:                  y1                y1                 y1
#>                                                                         
#> Constant          4.191*** (0.0970) 4.248*** (0.4114)  2.381*** (0.4493)
#> x1               0.5418*** (0.0693)   0.3990 (0.2958) 0.9342*** (0.1693)
#> x2                -0.3196* (0.1605)   0.7121 (0.4874)   -0.3200 (0.4024)
#> ________________ __________________ _________________ __________________
#> S.E. type                       IID               IID                IID
#> Observations                    150                50                 50
#> R2                          0.76626           0.11173            0.57432
#> Adj. R2                     0.76308           0.07393            0.55620
#> 
#>                  feols(y1 ~ x1 +..4
#> Sample (species)          virginica
#> Dependent Var.:                  y1
#>                                    
#> Constant            1.052* (0.5139)
#> x1               0.9946*** (0.0893)
#> x2                  0.0071 (0.1795)
#> ________________ __________________
#> S.E. type                       IID
#> Observations                     50
#> R2                          0.74689
#> Adj. R2                     0.73612
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
12.4.6.2.4 Standard Errors

  • iid: errors are homoskedastic and independent and identically distributed

  • hetero: errors are heteroskedastic using White correction

  • cluster: errors are correlated within the cluster groups

  • newey_west: (Newey and West 1986) use for time series or panel data. Errors are heteroskedastic and serially correlated.

    • vcov = newey_west ~ id + period where id is the subject id and period is time period of the panel.

    • to specify lag period to consider vcov = newey_west(2) ~ id + period where we’re considering 2 lag periods.

  • driscoll_kraay (Driscoll and Kraay 1998) use for panel data. Errors are cross-sectionally and serially correlated.

    • vcov = discoll_kraay ~ period

  • conley: (Conley 1999) for cross-section data. Errors are spatially correlated

    • vcov = conley ~ latitude + longitude

    • to specify the distance cutoff, vcov = vcov_conley(lat = "lat", lon = "long", cutoff = 100, distance = "spherical"), which will use the conley() helper function.

  • hc: from the sandwich package

    • vcov = function(x) sandwich::vcovHC(x, type = "HC1"))

To let R know which SE estimation you want to use, insert vcov = vcov_type ~ variables

12.4.6.2.5 Small sample correction

To specify that R needs to use small sample correction add

ssc = ssc(adj = T, cluster.adj = T)

References

Ahrens, Henry, and Robert Pincus. 1981. “On Two Measures of Unbalancedness in a One-Way Model and Their Relation to Efficiency.” Biometrical Journal 23 (3): 227–35.
Amemiya, Takeshi. 1971. “The Estimation of the Variances in a Variance-Components Model.” International Economic Review, 1–13.
Amemiya, Takeshi, and Thomas E MaCurdy. 1986. “Instrumental-Variable Estimation of an Error-Components Model.” Econometrica: Journal of the Econometric Society, 869–80.
Babcock, Philip. 2010. “Real Costs of Nominal Grade Inflation? New Evidence from Student Course Evaluations.” Economic Inquiry 48 (4): 983–96.
Balestra, Pietro, and Jayalakshmi Varadharajan-Krishnakumar. 1987. “Full Information Estimations of a System of Simultaneous Equations with Error Component Structure.” Econometric Theory 3 (2): 223–46.
Baltagi, Badi H. 1981. “Simultaneous Equations with Error Components.” Journal of Econometrics 17 (2): 189–200.
Baltagi, Badi H, and Qi Li. 1991. “A Joint Test for Serial Correlation and Random Individual Effects.” Statistics & Probability Letters 11 (3): 277–80.
———. 1995. “Testing AR (1) Against MA (1) Disturbances in an Error Component Model.” Journal of Econometrics 68 (1): 133–51.
Bera, Anil K, Walter Sosa-Escudero, and Mann Yoon. 2001. “Tests for the Error Component Model in the Presence of Local Misspecification.” Journal of Econometrics 101 (1): 1–23.
Blau, David M. 1999. “The Effect of Income on Child Development.” Review of Economics and Statistics 81 (2): 261–76.
Breusch, Trevor S. 1978. “Testing for Autocorrelation in Dynamic Linear Models.” Australian Economic Papers 17 (31): 334–55.
Breusch, Trevor S, Grayham E Mizon, and Peter Schmidt. 1989. “Efficient Estimation Using Panel Data.” Econometrica: Journal of the Econometric Society, 695–700.
Breusch, Trevor S, and Adrian R Pagan. 1980. “The Lagrange Multiplier Test and Its Applications to Model Specification in Econometrics.” The Review of Economic Studies 47 (1): 239–53.
Conley, Timothy G. 1999. “GMM Estimation with Cross Sectional Dependence.” Journal of Econometrics 92 (1): 1–45.
Driscoll, John C, and Aart C Kraay. 1998. “Consistent Covariance Matrix Estimation with Spatially Dependent Panel Data.” Review of Economics and Statistics 80 (4): 549–60.
Godfrey, Leslie G. 1978. “Testing Against General Autoregressive and Moving Average Error Models When the Regressors Include Lagged Dependent Variables.” Econometrica: Journal of the Econometric Society, 1293–1301.
Gourieroux, Christian, Alberto Holly, and Alain Monfort. 1982. “Likelihood Ratio Test, Wald Test, and Kuhn-Tucker Test in Linear Models with Inequality Constraints on the Regression Parameters.” Econometrica: Journal of the Econometric Society, 63–80.
Honda, Yuzo. 1985. “Testing the Error Components Model with Non-Normal Disturbances.” The Review of Economic Studies 52 (4): 681–90.
King, Maxwell L, and Ping X Wu. 1997. “Locally Optimal One-Sided Tests for Multiparameter Hypotheses.” Econometric Reviews 16 (2): 131–56.
Narayanan, Sridhar, and Harikesh S Nair. 2013. “Estimating Causal Installed-Base Effects: A Bias-Correction Approach.” Journal of Marketing Research 50 (1): 70–94.
Nerlove, Marc. 1971. “Further Evidence on the Estimation of Dynamic Economic Relations from a Time Series of Cross Sections.” Econometrica: Journal of the Econometric Society, 359–82.
Newey, Whitney K, and Kenneth D West. 1986. “A Simple, Positive Semi-Definite, Heteroskedasticity and Autocorrelationconsistent Covariance Matrix.”
Nickell, Stephen. 1981. “Biases in Dynamic Models with Fixed Effects.” Econometrica: Journal of the Econometric Society, 1417–26.
Swamy, PAVB, and Swarnjit S Arora. 1972. “The Exact Finite Sample Properties of the Estimators of Coefficients in the Error Components Regression Models.” Econometrica: Journal of the Econometric Society, 261–75.
Wallace, T Dudley, and Ashiq Hussain. 1969. “The Use of Error Components Models in Combining Cross Section with Time Series Data.” Econometrica: Journal of the Econometric Society, 55–72.