19.3 Rerandomization
Since randomization only balances baseline covariates on average, imbalance in variables due to random chance can still happen.
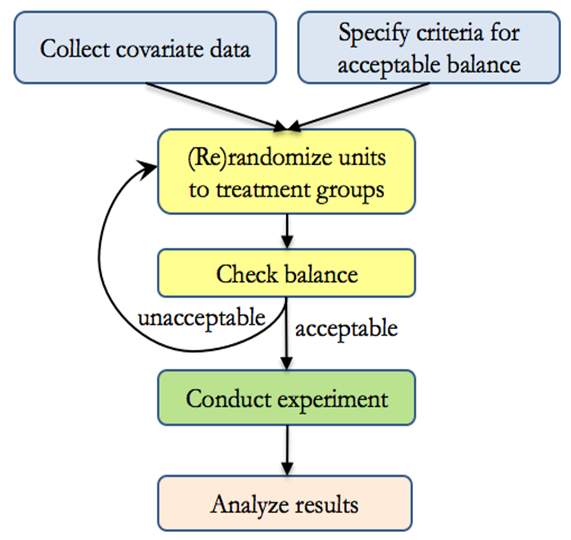
In case that you have a “bad” randomization (i.e., imbalance for important baseline covariates), (Morgan and Rubin 2012) introduce the idea of rerandomization.
Rerandomization is checking balance during the randomization process (before the experiment), to eliminate bad allocation (i.e., those with unacceptable balance).
The greater the number of variables, the greater the likelihood that at least one covariate would be imbalanced across treatment groups.
- Example: For 10 covariates, the probability of a significant difference at \(\alpha = .05\) for at least one covariate is \(1 - (1-.05)^{10} = 0.4 = 40\%\)
Rerandomization increase treatment effect estimate precision if the covariates are correlated with the outcome.
- Improvement in precision for treatment effect estimate depends on (1) improvement in covariate balance and (2) correlation between covariates and the outcome.
You also need to take into account rerandomization into your analysis when making inference.
Rerandomization is equivalent to increasing our sample size.
Alternatives include
Stratified randomization (Johansson and Schultzberg 2022)
Matched randomization (Greevy et al. 2004; Kapelner and Krieger 2014)
Minimization (Pocock and Simon 1975)
Rerandomization Criterion
- Acceptable randomization is based on a function of covariate matrix \(\mathbf{X}\) and vector of treatment assignments \(\mathbf{W}\)
\[ W_i = \begin{cases} 1 \text{ if treated} \\ 0 \text{ if control} \end{cases} \]
- Mahalanobis Distance, \(M\), can be used as criteria for acceptable balance
Let \(M\) be the multivariate distance between groups means
\[ \begin{aligned} M &= (\bar{\mathbf{X}}_T - \bar{\mathbf{X}}_C)' cov(\bar{\mathbf{X}}_T - \bar{\mathbf{X}}_C)^{-1} (\bar{\mathbf{X}}_T - \bar{\mathbf{X}}_C) \\ &= (\frac{1}{n_T}+ \frac{1}{n_C})^{-1}(\bar{\mathbf{X}}_T - \bar{\mathbf{X}}_C)' cov(\mathbf{X})^{-1}(\bar{\mathbf{X}}_T - \bar{\mathbf{X}}_C) \end{aligned} \]
With large sample size and “pure” randomization \(M \sim \chi^2_k\) where \(k\) is the number of covariates to be balanced
Then let \(p_a\) be the probability of accepting a randomization. Choosing appropriate \(p_a\) is a tradeoff between balance and time.
Then the rule of thumb is re-randomize when \(M > a\)