39.2 Good Controls

39.2.1 Omitted Variable Bias Correction

This is when \(Z\) can block all back-door paths.

rm(list = ls())

model <- dagitty("dag{x->y; z->x; z->y}")

## coordinates for plotting
coordinates(model) <-  list(
  x = c(x=1, y=3, z=2),
  y = c(x=1, y=1, z=2))

## ggplot
ggdag(model) + theme_dag()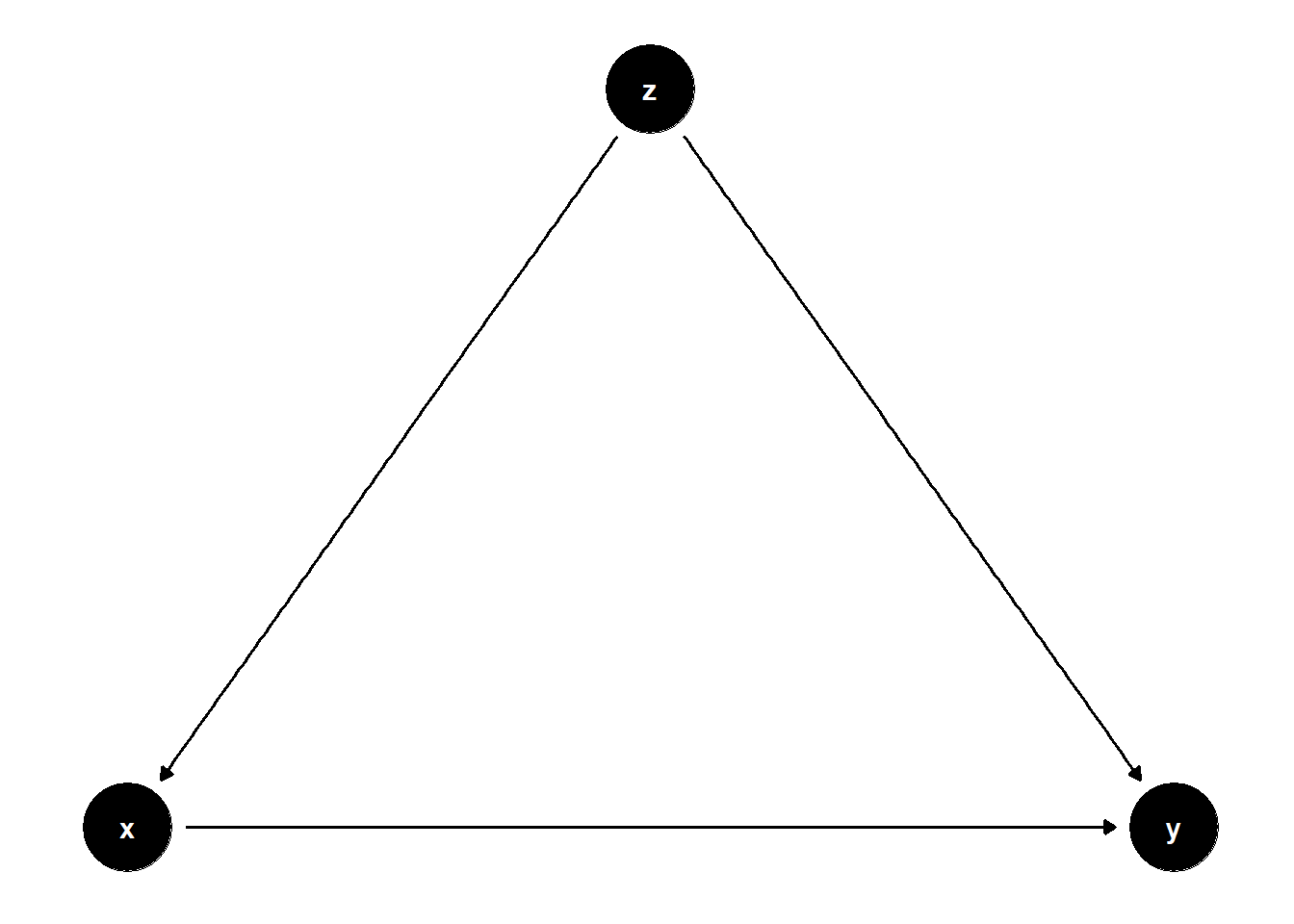

Unadjusted estimate is biased

adjusting for \(Z\) blocks the backdoor path

n <- 1e4
z <- rnorm(n)
causal_coef = 2
beta2 = 3
x <- z + rnorm(n)
y <- causal_coef * x + beta2 * z + rnorm(n)

jtools::export_summs(lm(y ~ x), lm(y ~ x + z))
Table 38.9:
Model 1Model 2
(Intercept)0.01    -0.00    
(0.02)   (0.01)   
x3.51 ***2.00 ***
(0.02)   (0.01)   
z       3.02 ***
       (0.01)   
N10000       10000       
R20.82    0.97    
*** p < 0.001; ** p < 0.01; * p < 0.05.
# cleans workspace
rm(list = ls())

# Draw DAG

# specify edges
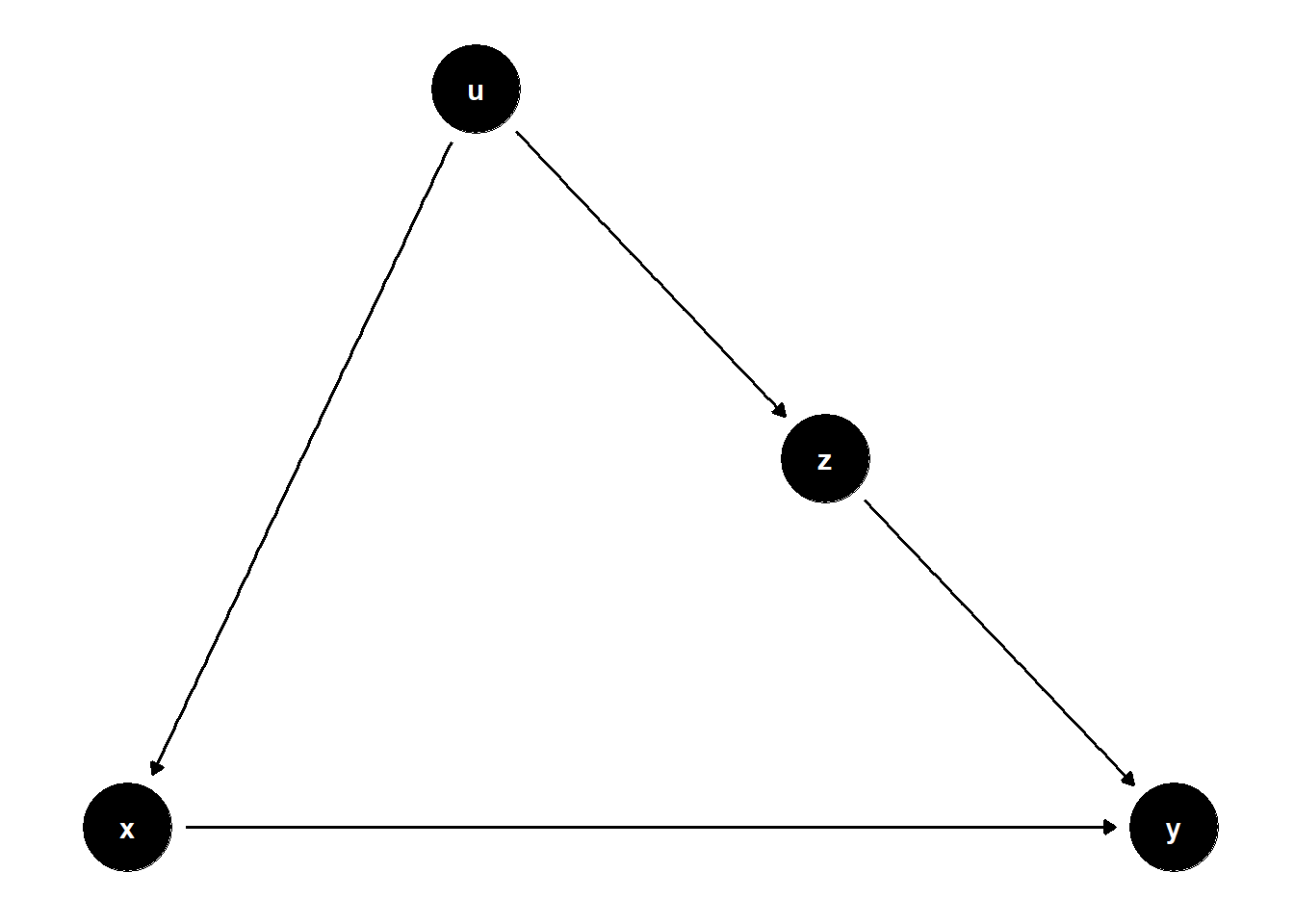
model <- dagitty("dag{x->y; u->z; z->x; u->y}")

# set u as latent
latents(model) <- "u"

## coordinates for plotting
coordinates(model) <-  list(
  x = c(x=1, z=2, u=3, y = 4),
  y = c(x=1, y=1, z=2, u = 3))

## ggplot
ggdag(model) + theme_dag()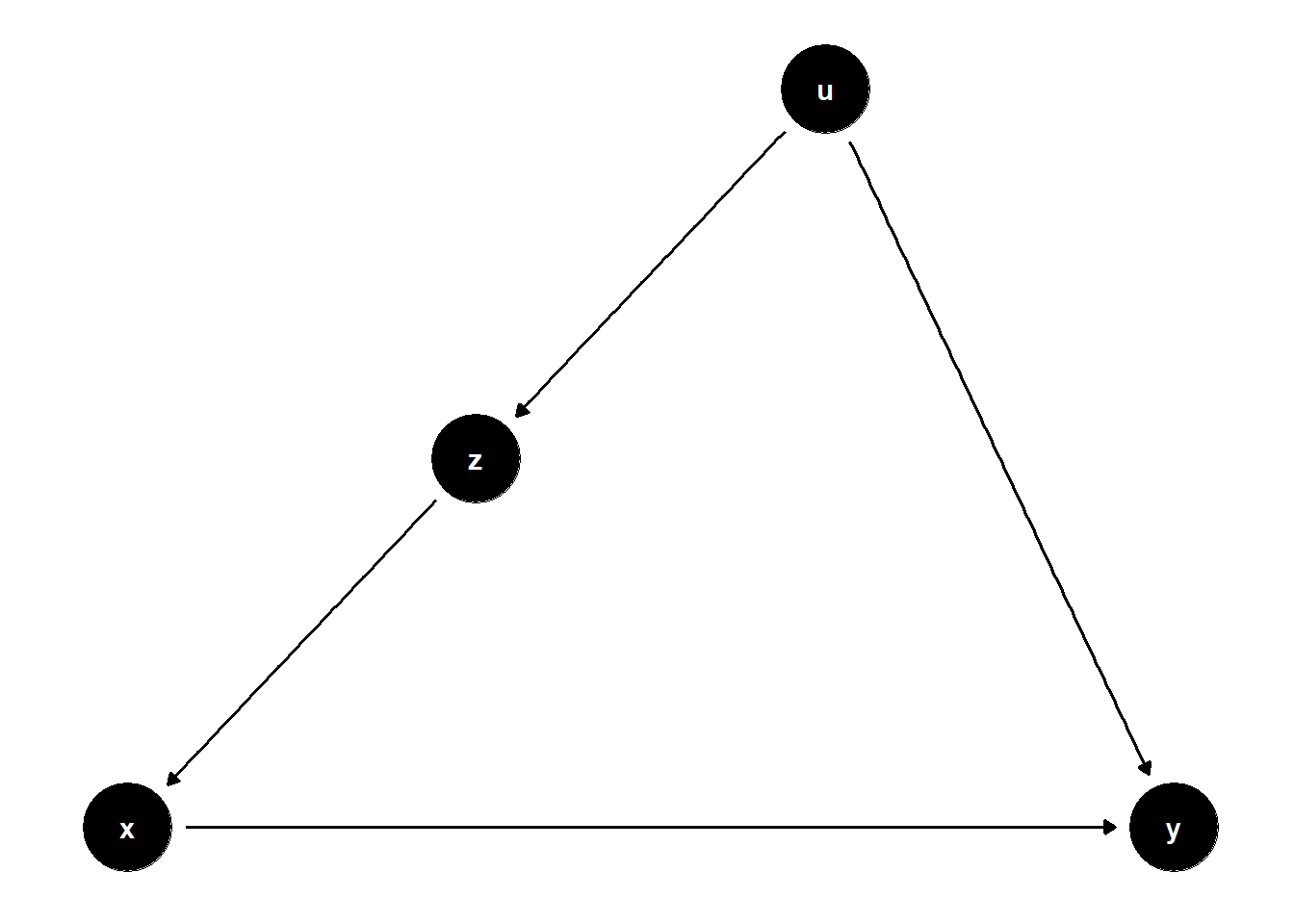

Unadjusted estimate is biased

adjusting for \(Z\) blocks the backdoor door path due to \(U\)

n <- 1e4
u <- rnorm(n)
z <- u + rnorm(n)
causal_coef = 2
x <- z + rnorm(n)
y <- causal_coef * x + u + rnorm(n)

jtools::export_summs(lm(y ~ x), lm(y ~ x + z))
Table 38.10:
Model 1Model 2
(Intercept)0.03 *  0.03 *  
(0.01)   (0.01)   
x2.34 ***2.01 ***
(0.01)   (0.01)   
z       0.49 ***
       (0.01)   
N10000       10000       
R20.91    0.92    
*** p < 0.001; ** p < 0.01; * p < 0.05.

Even though \(Z\) is significant, we cannot give it a causal interpretation.

# cleans workspace
rm(list = ls())

# Draw DAG

# specify edges
model <- dagitty("dag{x->y; u->z; u->x; z->y}")

# set u as latent
latents(model) <- "u"

## coordinates for plotting
coordinates(model) <-  list(
  x = c(x=1, z=3, u=2, y = 4),
  y = c(x=1, y=1, z=2, u = 3))

## ggplot
ggdag(model) + theme_dag()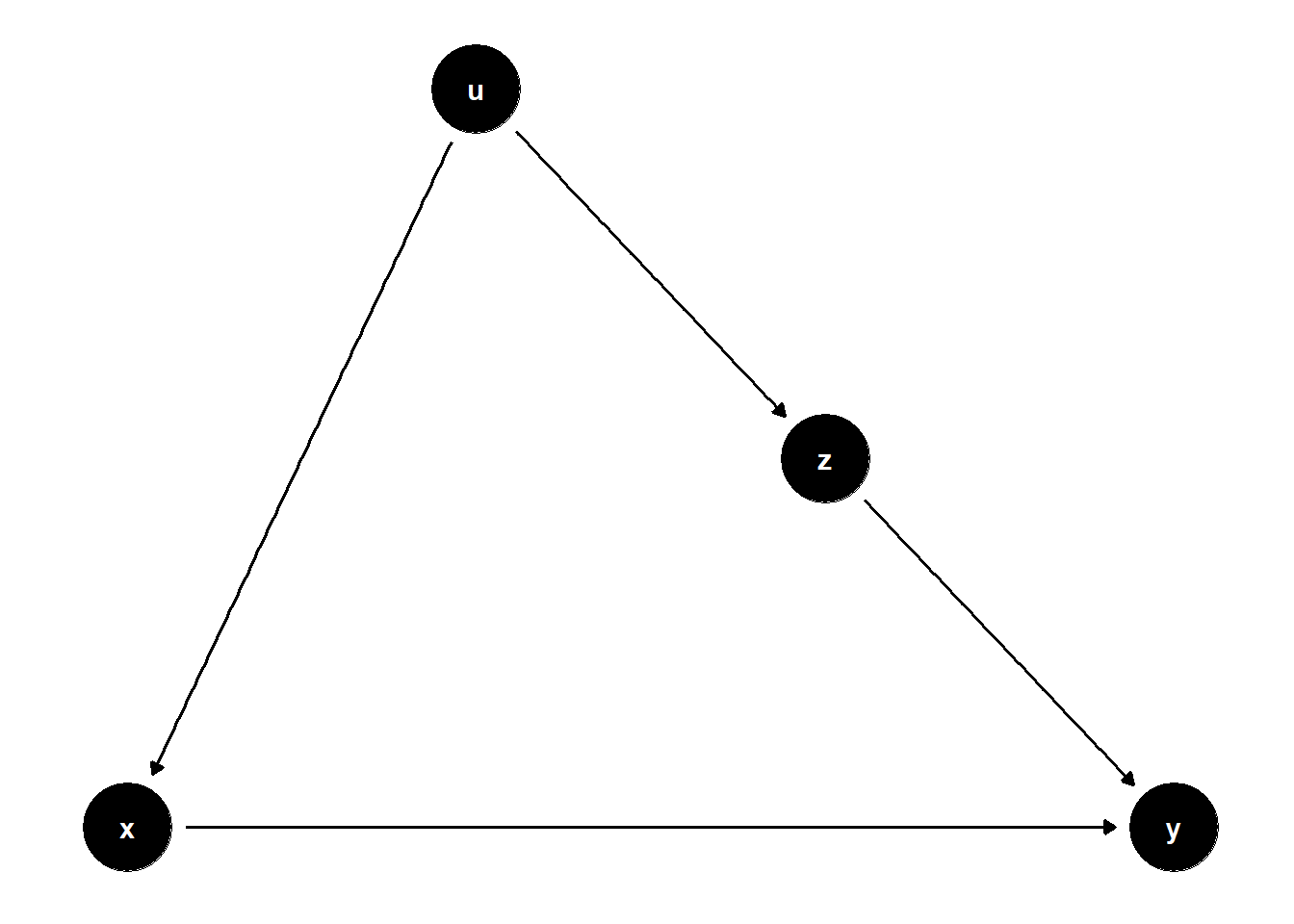

n     <- 1e4
u     <- rnorm(n)
z     <- u + rnorm(n)
x     <- u + rnorm(n)
causal_coef <- 2
y     <- causal_coef * x + z + rnorm(n)

jtools::export_summs(lm(y ~ x), lm(y ~ x + z))
Table 17.1:
Model 1Model 2
(Intercept)-0.03    -0.01    
(0.02)   (0.01)   
x2.51 ***2.01 ***
(0.01)   (0.01)   
z       1.01 ***
       (0.01)   
N10000       10000       
R20.84    0.93    
*** p < 0.001; ** p < 0.01; * p < 0.05.

Even though \(Z\) is significant, we cannot give it a causal interpretation.

Summary

# cleans workspace
rm(list = ls())

# Model 1 

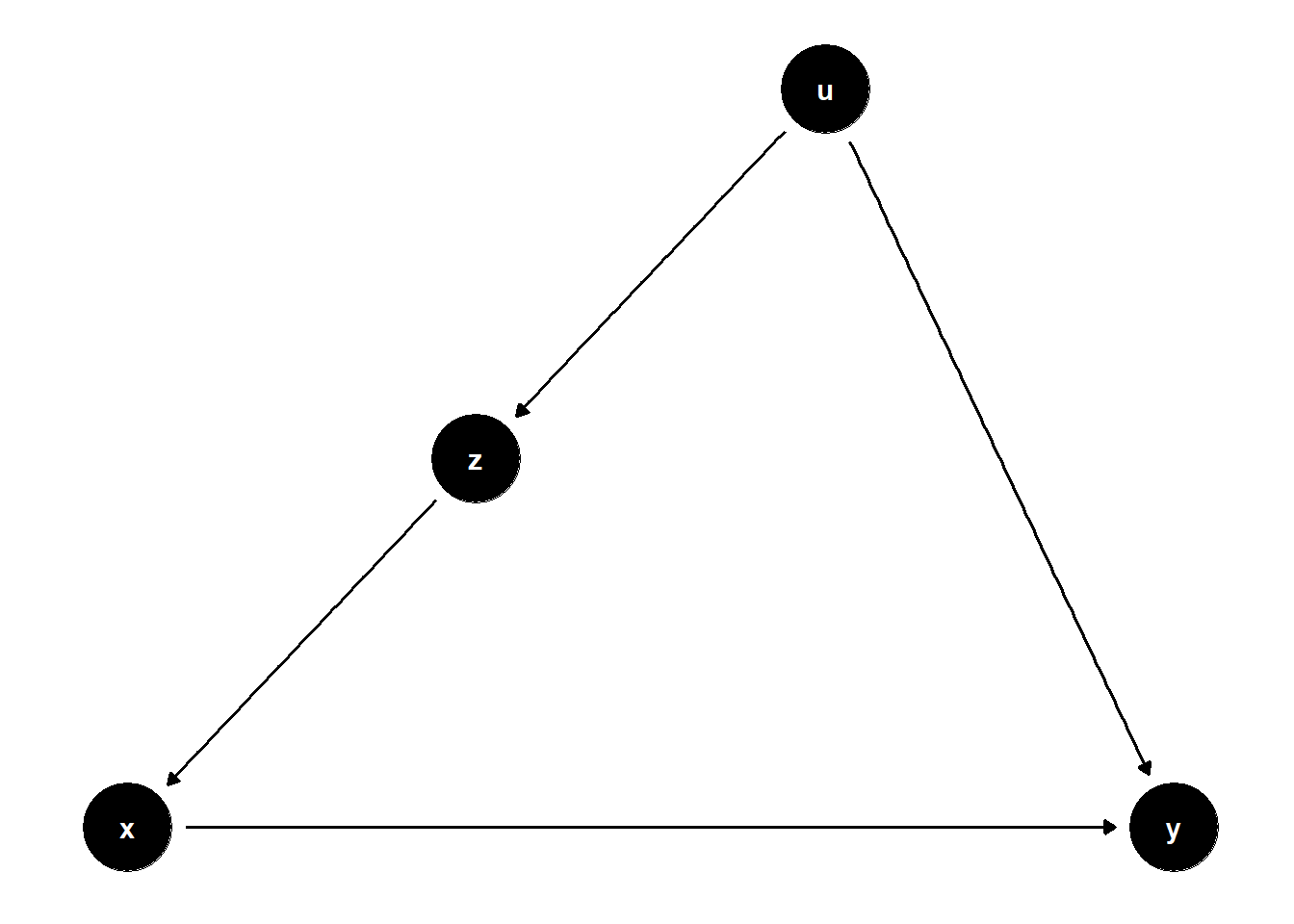
model1 <- dagitty("dag{x->y; z->x; z->y}")

## coordinates for plotting
coordinates(model1) <-  list(
  x = c(x=1, y=3, z=2),
  y = c(x=1, y=1, z=2))



# Model 2

# specify edges
model2 <- dagitty("dag{x->y; u->z; z->x; u->y}")

# set u as latent
latents(model2) <- "u"

## coordinates for plotting
coordinates(model2) <-  list(
  x = c(x=1, z=2, u=3, y = 4),
  y = c(x=1, y=1, z=2, u = 3))



# Model 3

# specify edges
model3 <- dagitty("dag{x->y; u->z; u->x; z->y}")

# set u as latent
latents(model3) <- "u"

## coordinates for plotting
coordinates(model3) <-  list(
  x = c(x=1, z=3, u=2, y = 4),
  y = c(x=1, y=1, z=2, u = 3))

par(mfrow=c(1,3))

## ggplot
ggdag(model1) + theme_dag()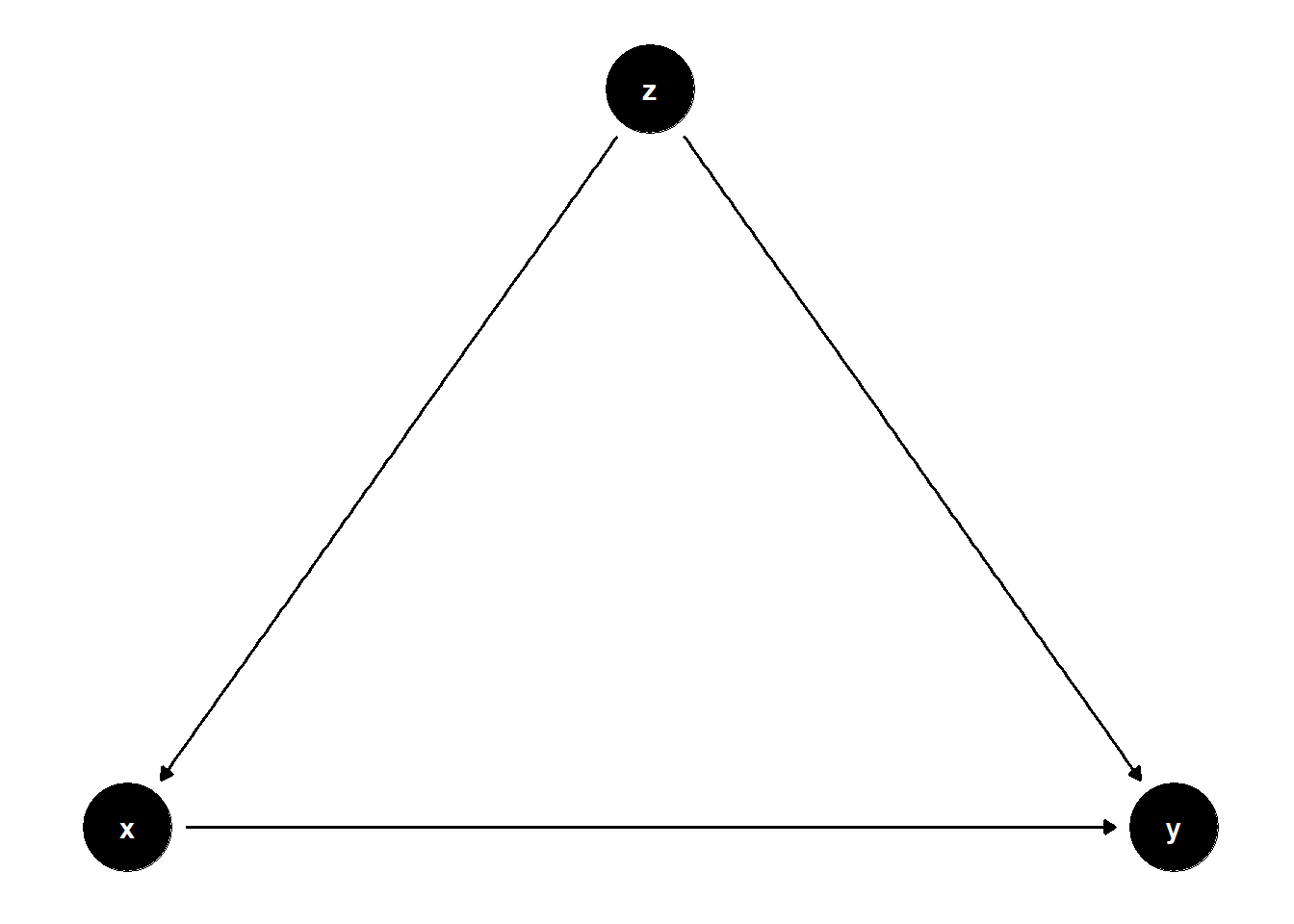


## ggplot
ggdag(model2) + theme_dag()


## ggplot
ggdag(model3) + theme_dag()

39.2.2 Omitted Variable Bias in Mediation Correction

Common causes of \(X\) and any mediator (between \(X\) and \(Y\)) confound the effect of \(X\) on \(Y\)

# cleans workspace
rm(list = ls())

# DAG

## specify edges
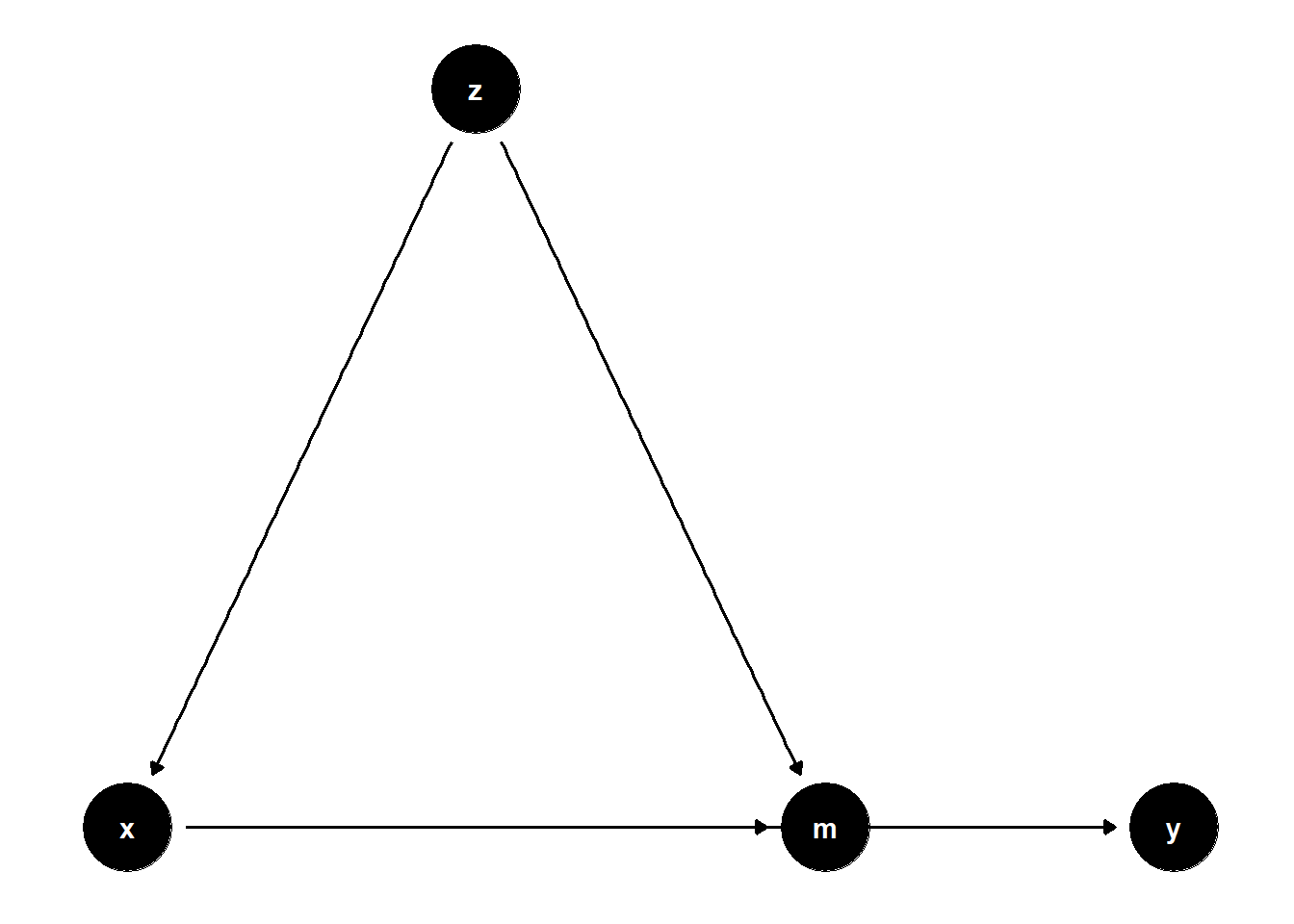
model <- dagitty("dag{x->y; z->x; x->m; z->m; m->y}")

## coordinates for plotting
coordinates(model) <-  list(
  x = c(x=1, z=2, m=3, y=4),
  y = c(x=1, z=2, m=1, y=1))

## ggplot
ggdag(model) + theme_dag()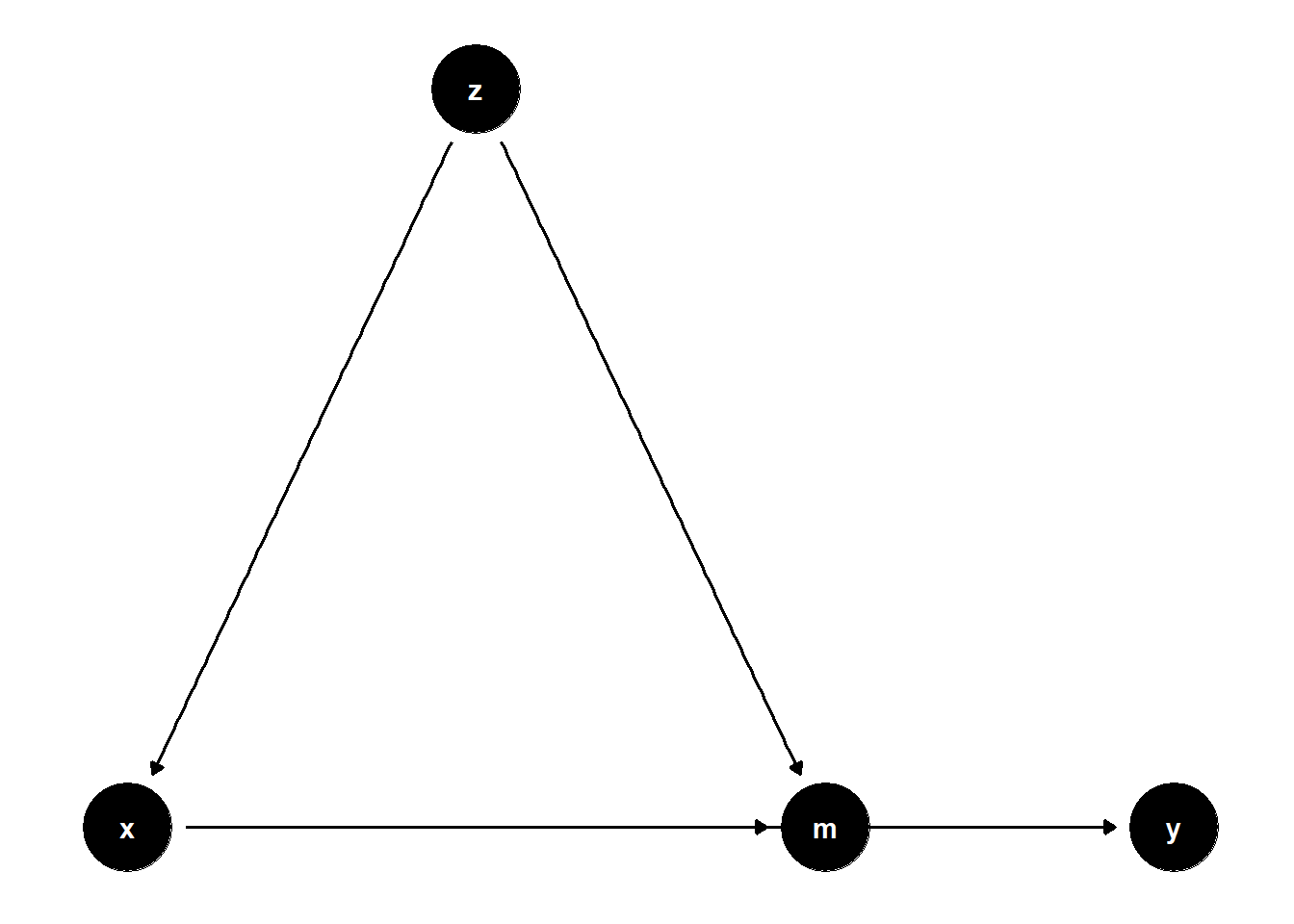

\(Z\) is a confounder of both the mediator \(M\) and \(X\)

n     <- 1e4
z     <- rnorm(n)
x     <- z + rnorm(n)
causal_coef <- 2
m     <- causal_coef * x + z + rnorm(n)
y     <- m + rnorm(n)

jtools::export_summs(lm(y ~ x), lm(y ~ x + z))
Table 38.11:
Model 1Model 2
(Intercept)-0.02    -0.01    
(0.02)   (0.01)   
x2.49 ***1.97 ***
(0.01)   (0.01)   
z       1.02 ***
       (0.02)   
N10000       10000       
R20.83    0.86    
*** p < 0.001; ** p < 0.01; * p < 0.05.
# cleans workspace
rm(list = ls())

# DAG

## specify edges
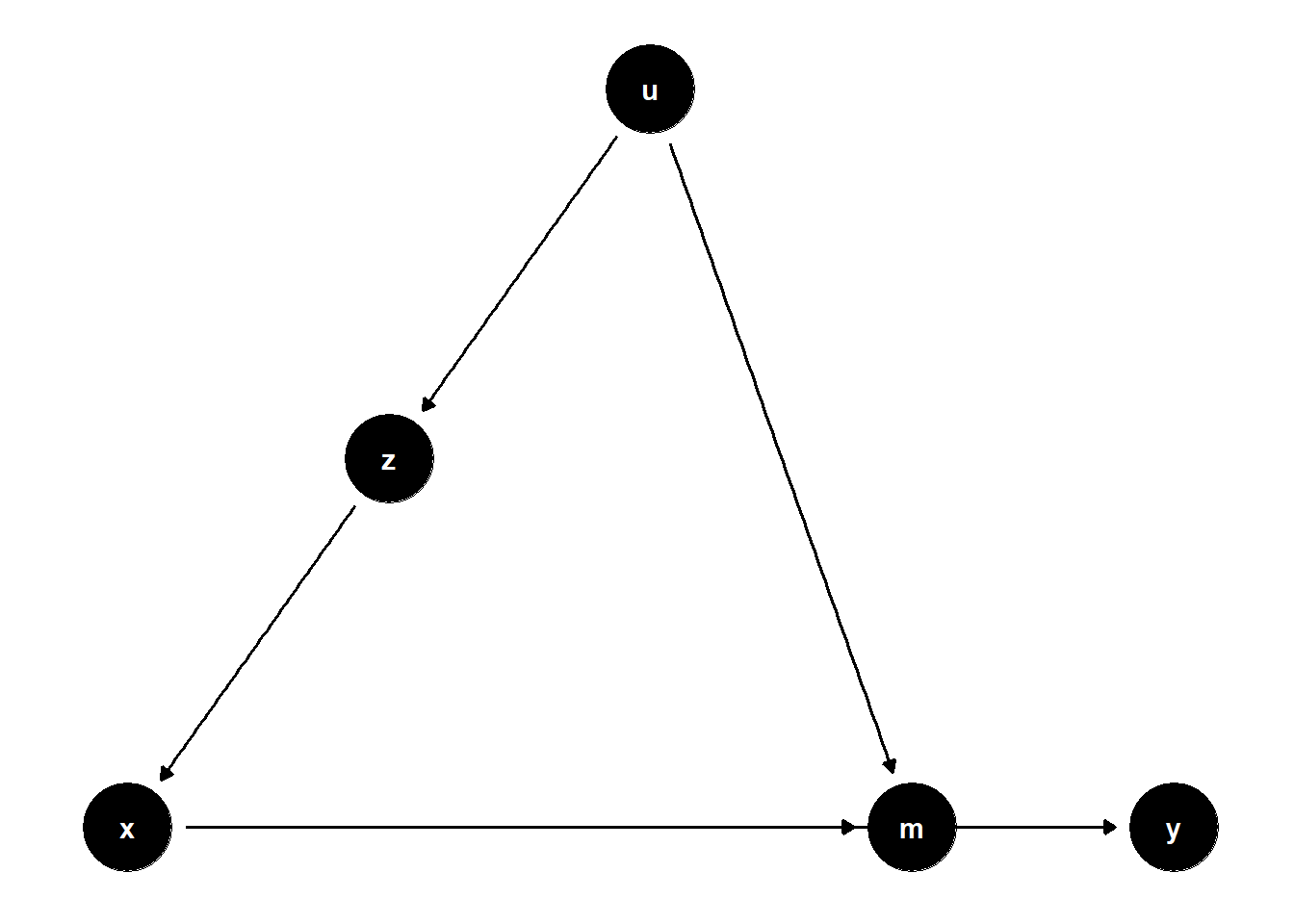
model <- dagitty("dag{x->y; u->z; z->x; x->m; u->m; m->y}")

# set u as latent
latents(model) <- "u"

## coordinates for plotting
coordinates(model) <-  list(
  x = c(x=1, z=2, u=3, m=4, y=5),
  y = c(x=1, z=2, u=3, m=1, y=1))

## ggplot
ggdag(model) + theme_dag()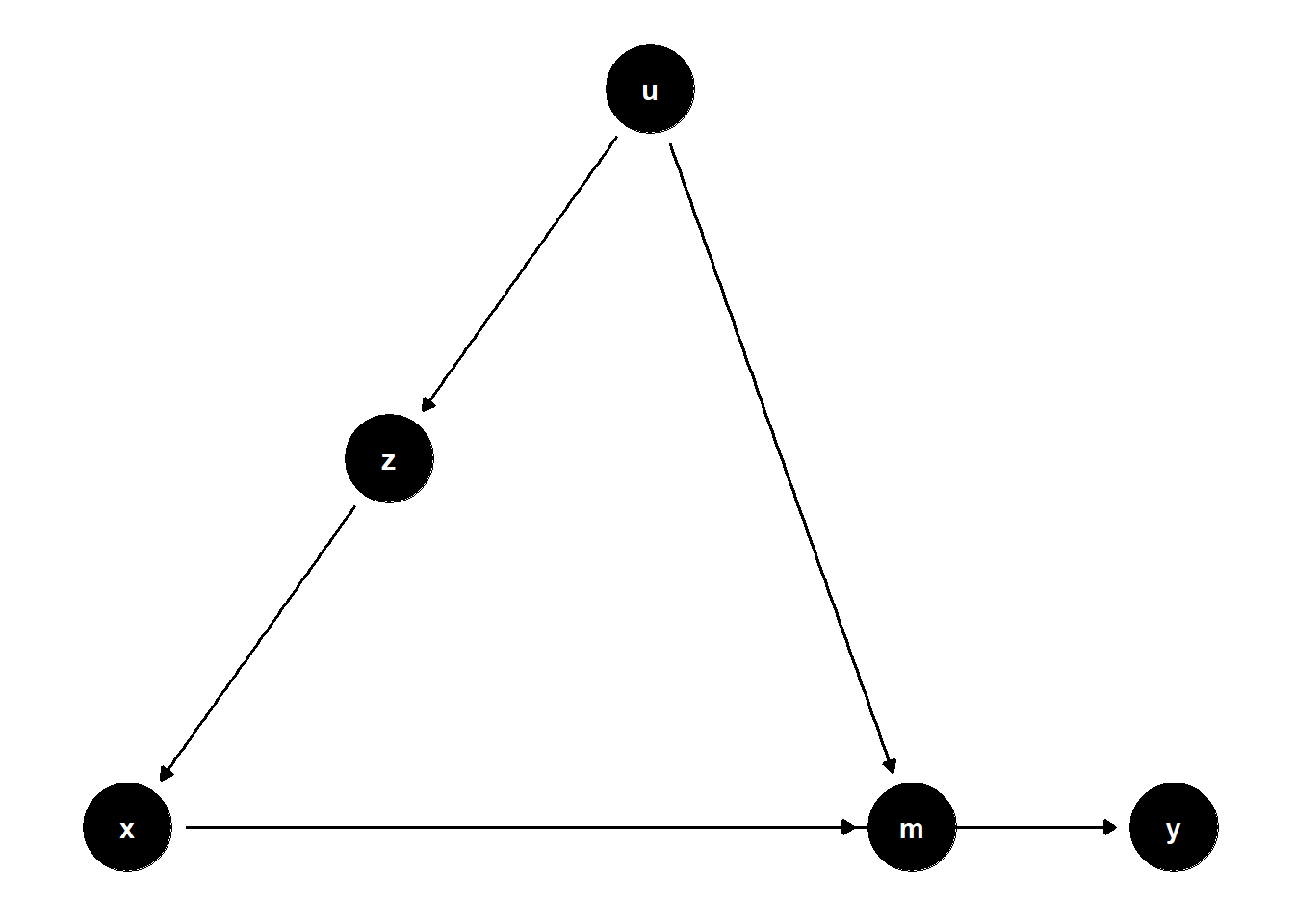

n     <- 1e4
u     <- rnorm(n)
z     <- u + rnorm(n)
x     <- z + rnorm(n)
causal_coef <- 2
m     <- causal_coef * x + u + rnorm(n)
y     <- m + rnorm(n)

jtools::export_summs(lm(y ~ x), lm(y ~ x + z))
Table 17.2:
Model 1Model 2
(Intercept)-0.01    -0.01    
(0.02)   (0.02)   
x2.31 ***2.00 ***
(0.01)   (0.02)   
z       0.49 ***
       (0.02)   
N10000       10000       
R20.86    0.86    
*** p < 0.001; ** p < 0.01; * p < 0.05.
# cleans workspace
rm(list = ls())

# DAG

## specify edges
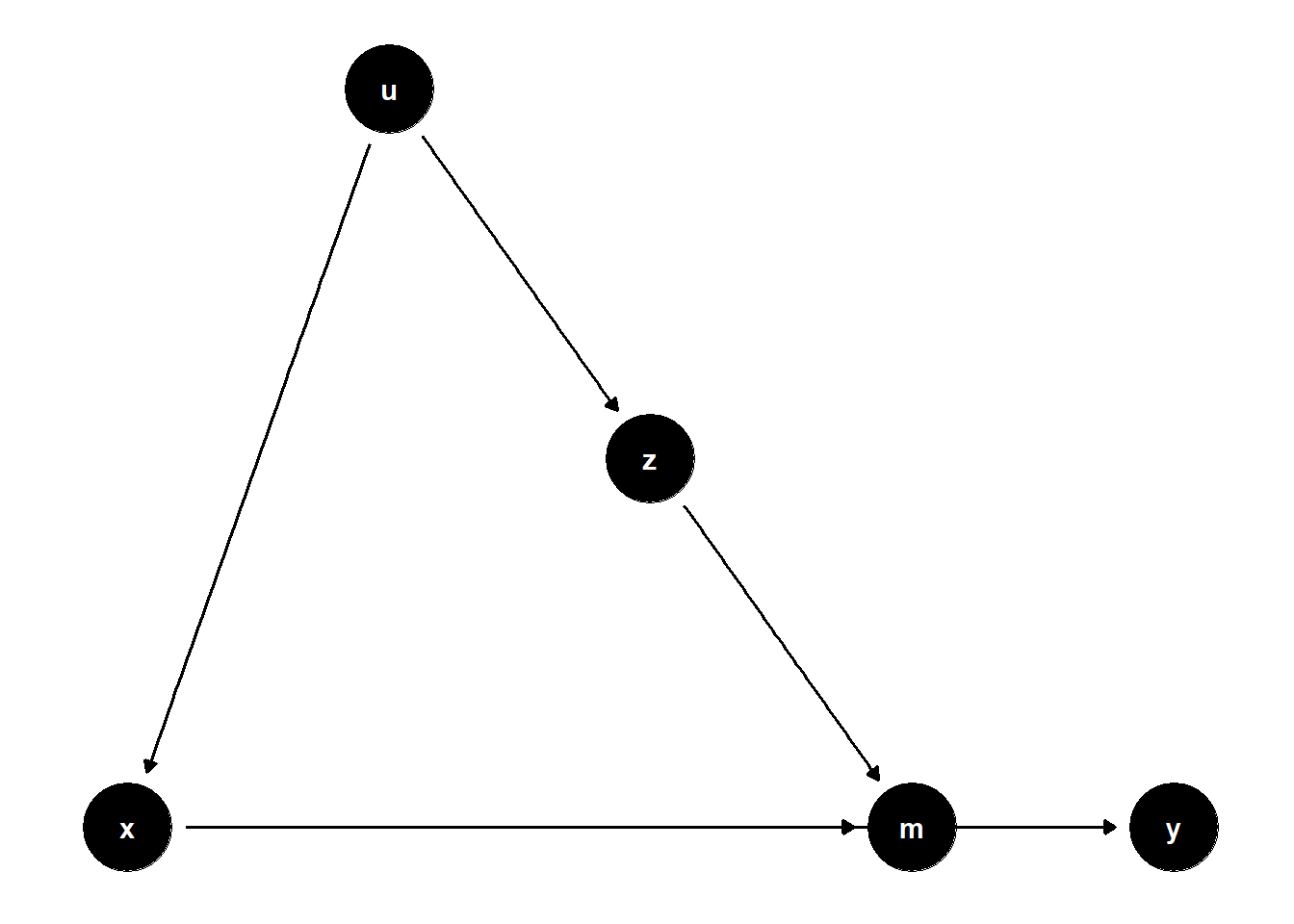
model <- dagitty("dag{x->y; u->z; z->m; x->m; u->x; m->y}")

# set u as latent
latents(model) <- "u"

## coordinates for plotting
coordinates(model) <-  list(
  x = c(x=1, z=3, u=2, m=4, y=5),
  y = c(x=1, z=2, u=3, m=1, y=1))

## ggplot
ggdag(model) + theme_dag()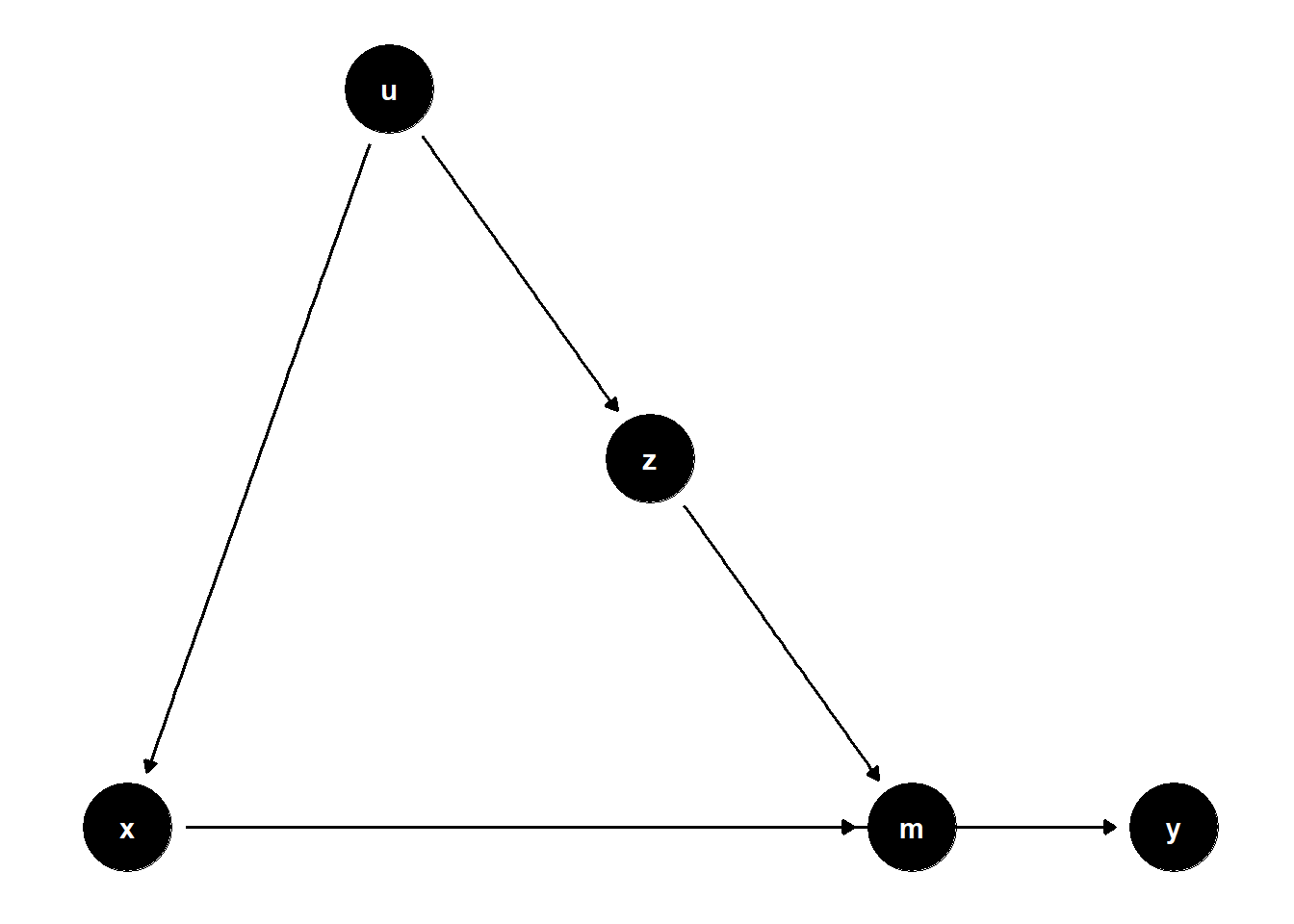

n     <- 1e4
u     <- rnorm(n)
z     <- u + rnorm(n)
x     <- u + rnorm(n)
causal_coef <- 2
m     <- causal_coef * x + z + rnorm(n)
y     <- m + rnorm(n)

jtools::export_summs(lm(y ~ x), lm(y ~ x + z))
Table 38.12:
Model 1Model 2
(Intercept)0.01    -0.00    
(0.02)   (0.01)   
x2.50 ***1.99 ***
(0.01)   (0.01)   
z       1.02 ***
       (0.01)   
N10000       10000       
R20.78    0.87    
*** p < 0.001; ** p < 0.01; * p < 0.05.

Summary

# model 4
model4 <- dagitty("dag{x->y; z->x; x->m; z->m; m->y}")

## coordinates for plotting
coordinates(model4) <-  list(
  x = c(x=1, z=2, m=3, y=4),
  y = c(x=1, z=2, m=1, y=1))


# model 5
model5 <- dagitty("dag{x->y; u->z; z->x; x->m; u->m; m->y}")

# set u as latent
latents(model5) <- "u"

## coordinates for plotting
coordinates(model5) <-  list(
  x = c(x=1, z=2, u=3, m=4, y=5),
  y = c(x=1, z=2, u=3, m=1, y=1))


# model 6

model6 <- dagitty("dag{x->y; u->z; z->m; x->m; u->x; m->y}")

# set u as latent
latents(model6) <- "u"

## coordinates for plotting
coordinates(model6) <-  list(
  x = c(x=1, z=3, u=2, m=4, y=5),
  y = c(x=1, z=2, u=3, m=1, y=1))

par(mfrow=c(1,3))

## ggplot
ggdag(model4) + theme_dag()


## ggplot
ggdag(model5) + theme_dag()


## ggplot
ggdag(model6) + theme_dag()