28.9 Validity and hypothesis testing
When performing hypothesis tests, certain statistical validity conditions must be true. These conditions ensure that the sampling distribution is sufficiently close to a normal distribution for the 68–95–99.7 rule rule to apply and hence for \(P\)-values to be computed13.
If these conditions are not met, the sampling distribution may not be normally distributed, so the \(P\)-values (and hence conclusions) maybe inappropriate.
In addition to the statistical validity condition, the internal validity and external validity of the study should be discussed also (Fig. 28.1). These are usually (but not always) the same as for CIs (Sect. 21.2).
Regarding external validity, all the computations in this book assume a simple random sample. If the sample is from a random sampling method, but not from a simple random sample, then methods exist for conducting hypothesis tests that are externally valid, but are more complicated than those described in this book.
If the sample is a non-random sample, then the hypothesis test may be reasonable for the quite specific population that is represented by the sample; however, the sample probably does not represent the more general population that is probably intended.
Externally validity requires that a study is also internally valid. Internal validity can only be discussed if details are known about the study design.
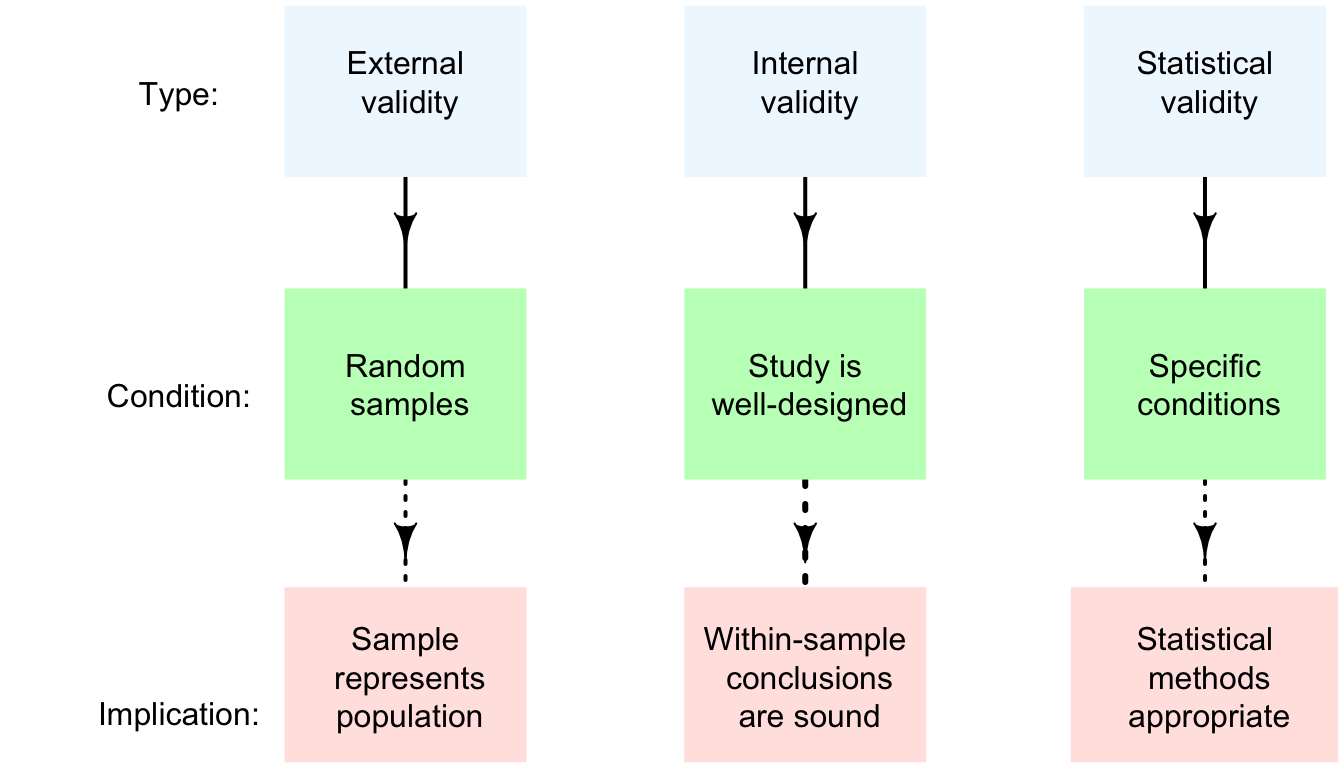
FIGURE 28.1: Three types of validities for studies.
In addition, hypothesis tests also require that the sample size is less than 10% of the population size; however this is almost always the case.
Not all sample statistics have normal distributions, but all the sample statistics in this book are either normally distributed or are closely related to normal distributions.↩︎