34.8 Exercises

Selected answers are available in Sect. D.31.

Exercise 34.1 Draw a scatterplot with:

A negative correlation coefficient, with the value of $r$ very close to (but not equal to) $-1$ .
A positive correlation coefficient, with the value of $r$ very close to (but not equal to) $+1$ .
A correlation coefficient very close to $0$ .

Exercise 34.2 A study (Myers (1990), p. 75) of American footballers measured the right-leg strengths $x$ of 13 players (using a weight lifting test), and the distance $y$ they punted a football (with their right leg) (Fig. 34.11).

The value of the correlation coefficient is 0.881. Compute the value of $R^2$ , and explain what this means.
jamovi was used to study the correlation (Fig. 34.12). Using this output, perform a hypothesis test to determine if a correlation exists between punting distance and right-leg strength.

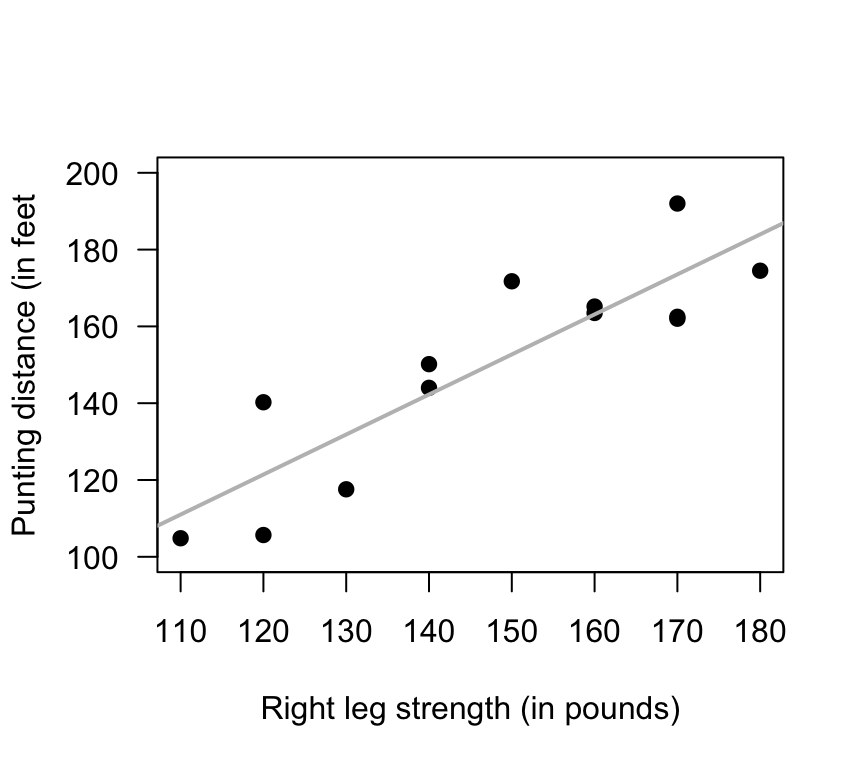
FIGURE 34.11: Punting distance and right leg strength

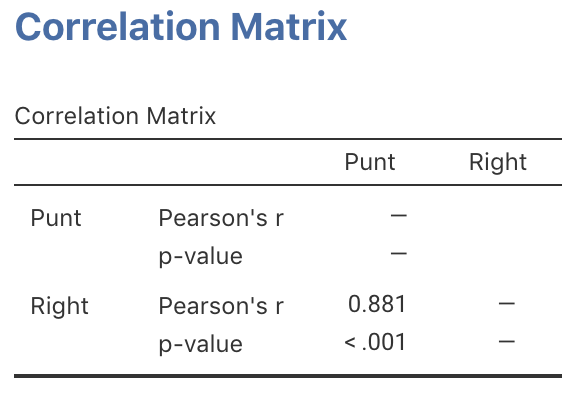
FIGURE 34.12: jamovi output for the punting data

Exercise 34.3 A study examined the time taken to deliver soft drinks to vending machines (Montgomery and Peck 1992) using a sample of size

$n=25$ (Fig. 34.13). To perform a test of the correlation coefficient, are the statistical validity conditions met?

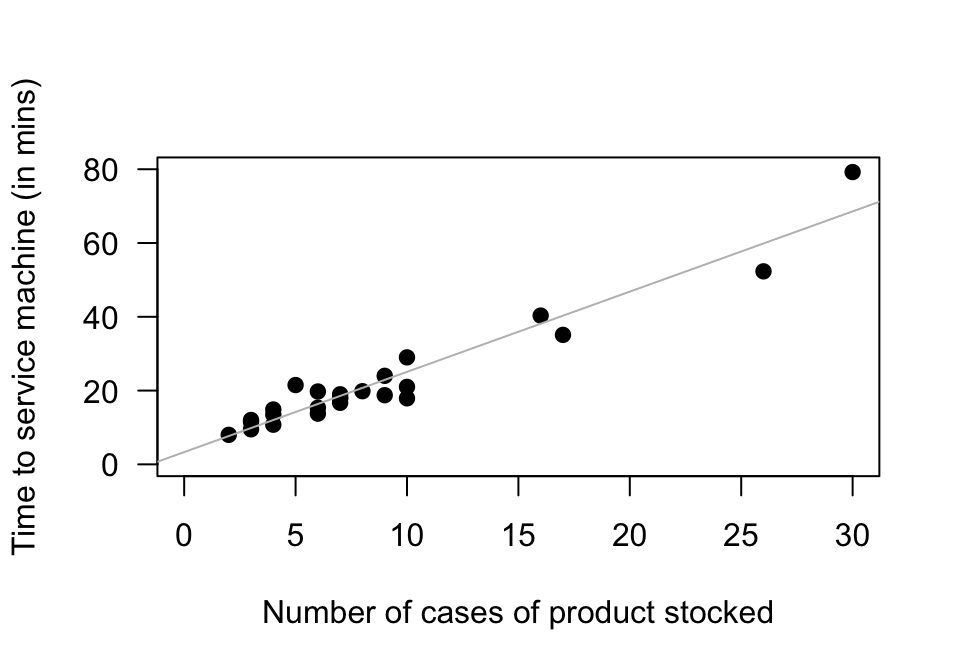
FIGURE 34.13: The time taken to deliver soft drinks to vending machines

Exercise 34.4 A study of hot mix asphalt (Panda et al. 2018) created $n=42$ samples of asphalt and measured the volume of air voids and the bitumen content by weight (Fig. 34.14).

Using the plot, estimate the value of $r$ .
The value of $R^2$ is 99.29%. What is the value of $r$ ? (Hint: Be careful!)
Would you expect the $P$ -value testing $H_0$ : $\rho=0$ to be small or large? Explain.
Would the test be statistically valid?

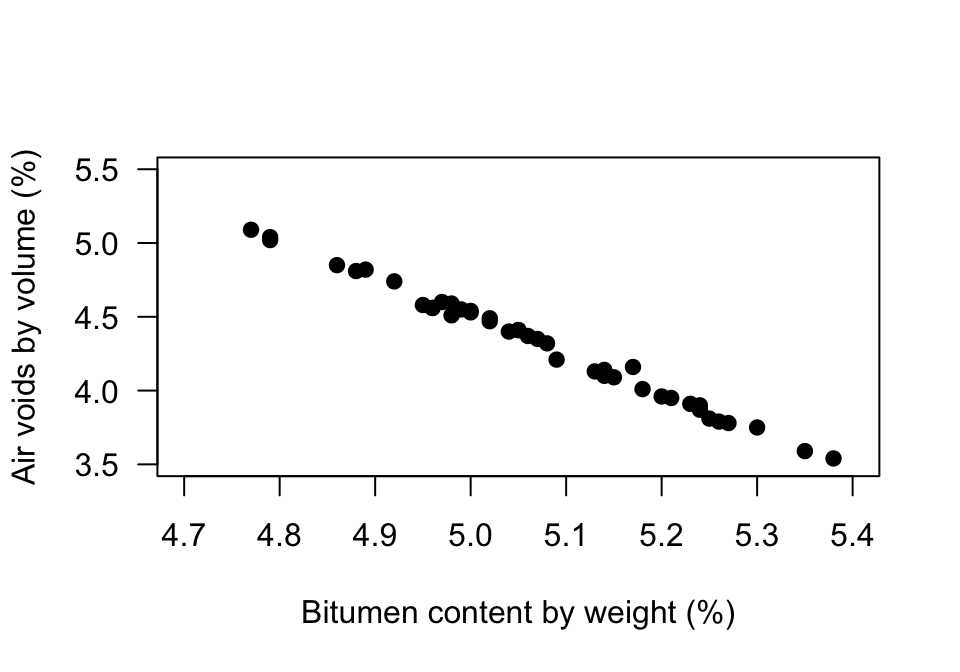
FIGURE 34.14: Air voids in bitumen samples

References

Montgomery DC, Peck EA. Introduction to regression analysis. New York: Wiley; 1992.

Myers RH. Classical and modern regression with applications. second. Duxbury; 1990.

Panda RP, Das SS, Sahoo PK. Relation between bitumen content and percentage air voids in semi dense bituminous concrete. Journal of The Institution of Engineers (India): Series A. 2018;99(2):327–32.