17.12 Exercises

Selected answers are available in Sect. D.17.

Exercise 17.1 Consider again the study by Aedo-Ortiz et al. (1997), who studied the diameter of trees in certain forests. The tree diameters can be modelled with

  • a normal distribution; with
  • a mean of \(\mu=8.8\) inches; and
  • a standard deviation of \(\sigma=2.7\) inches.

For these trees:

  1. What is the probability that a tree will have a diameter less than 8 inches?
  2. What is the probability that a tree will have a diameter greater than 9 inches?
  3. What is the probability that a tree will have a diameter between 7 and 10 inches?
  4. The largest 15% of trees have what diameters?
  5. The smallest 25% of trees have what diameters?

Exercise 17.2 In a study (Snowden and Basso 2018) to help understand factors influencing preterm births, the researchers modelled the gestation length of healthy babies as having a normal distribution with a mean of 40 weeks, and a standard deviation of 1.64 weeks. Using this model:

  1. What proportion of births are longer than 39 weeks (that is, nine months)?
  2. In Australia, a premature birth is defined as a birth occuring before 37 weeks. What proportion of births are expected to be premature?
  3. According to Health Direct, ‘Babies born between 32 and 37 weeks may need care in a special care nursery.’ What proportion of healthy births would be expected to be born between 32 and 37 weeks gestation?
  4. How long is the gestation length for the longest 5% of pregnancies?
  5. How long is the gestation length for the shortest 5% of pregnancies?

Exercise 17.3 IQ scores are designed to have a mean of 100 and a standard deviation of 15. Mensa is a society for people with a high IQ:

Membership of Mensa is open to persons who have attained a score within the upper two percent of the general population on an approved intelligence test that has been properly administered and supervised.

— Mensa webpage

What IQ score is needed to join Mensa?

Exercise 17.4 IQ scores are designed to have a mean of 100 and a standard deviation of 15. Zagorsky (2016) reports that

…Congress requires the Pentagon to reject all military recruits whose IQ is in the bottom 10% of the population…

— Zagorsky (2016), p. 403

What IQs scores lead to a rejection from the US military?

Exercise 17.5 IQ scores are designed to have a mean of 100 and a standard deviation of 15. Match the diagram in Fig. 17.14 with the meaning.

  1. IQs greater than 110.
  2. IQs between 90 and 115.
  3. IQs less than 110.
  4. IQs greater than 85.
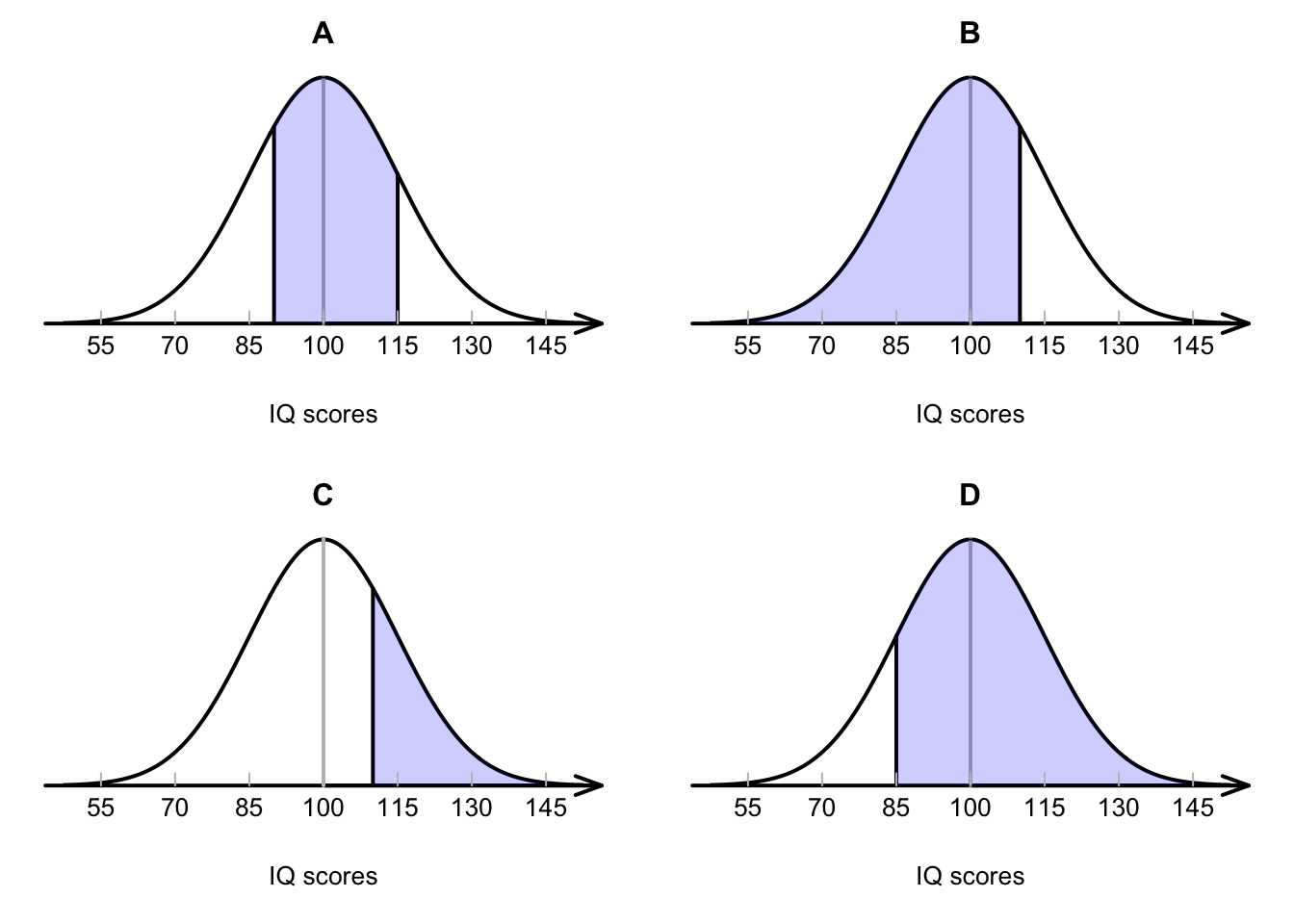
Match the diagram with the description

FIGURE 17.14: Match the diagram with the description

Exercise 17.6 IQ scores are designed to have a mean of 100 and a standard deviation of 15. Match the diagram in Fig. 17.14 with the meaning.

  1. The largest 25% of IQ scores.
  2. The smallest 10% of IQ scores.
  3. The largest 70% of IQ scores.
  4. The smallest 60% of IQ scores.
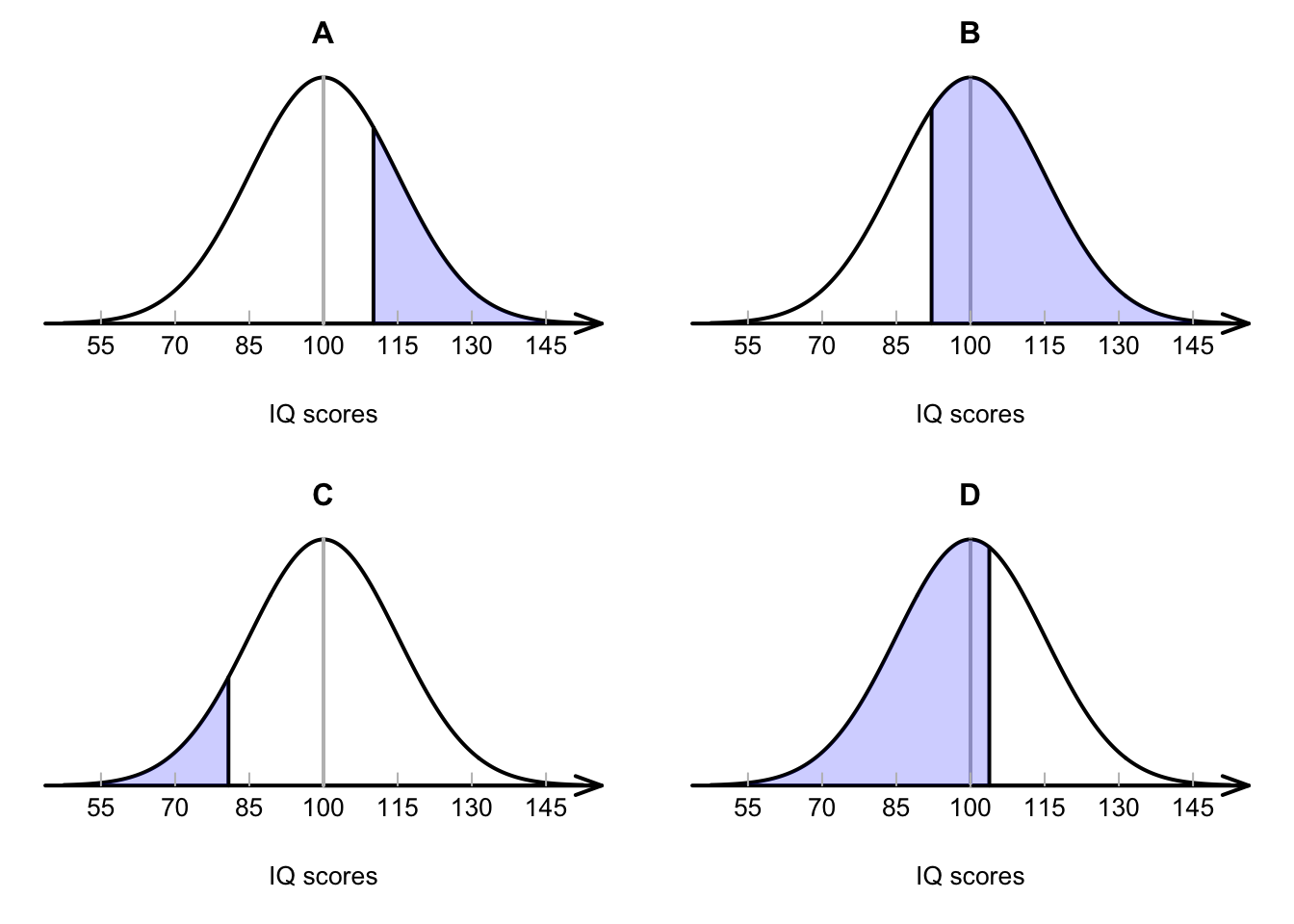
Match the diagram with the description

FIGURE 17.15: Match the diagram with the description

Exercise 17.7 A study of the impact of charging electric vehicles (EVs) on electricity demands (Affonso and Kezunovic 2018) modelled the time at which people began charging their EVs at home. Based on a survey (US Department of Transportation 2011), they modelled the time at which EVs began charging as having a mean of 5:30pm, with a standard deviation of 2.28 hrs. For this model:

  1. What is the probability that an EVs will begin charging after 9pm?
  2. What is the probability that an EVs will begin charging before 5pm?
  3. What is the probability that an EVs will begin charging between 5pm and 6pm?
  4. 30% of the EVs begin charging after what time?
  5. The earliest 15% of charging begins when?
Hint: This question is much easier if you convert times into ‘minutes after midnight.’

References

Aedo-Ortiz DM, Olsen ED, Kellogg LD. Simulating a harvester-forwarder softwood thinning: A software evaluation. Forest Products Journal. 1997;47(5):36–41.
Affonso CM, Kezunovic M. Probabilistic assessment of electric vehicle charging demand impact on residential distribution transformer aging. 2018 IEEE international conference on probabilistic methods applied to power systems (PMAPS). IEEE; 2018. p. 1–6.
Snowden JM, Basso O. Causal inference in studies of preterm babies: A simulation study. BJOG: An International Journal of Obstetrics & Gynaecology. Wiley Online Library; 2018;125(6):686–92.
US Department of Transportation. 2009 national household travel survey user’s guide. US Department of Transportation Washington, DC; 2011.
Zagorsky JL. Are blondes really dumb? Economics Bulletin. 2016;36(1):401–10.
Copyright © Peter K. Dunn, 2021