35.7 Confidence intervals

Reporting the CI for the slope is also useful, which can be obtained from software or computed manually.

Think 35.4 (Approximate 95% CI) Using the output (jamovi: Fig. 35.7; SPSS: Fig. 35.8), what is the approximate 95% CI for

$\beta_1$ ?

CIs have the form $\text{statistic} \pm ( \text{multiplier} \times \text{standard error}),$ The multiplier is two for an approximate 95% CI, so (using the standard error reported by the software), we obtain $-0.181 \pm (2\times 0.029)$ , or $-0.181 \pm 0.058$ , or from $-0.239$ to $-0.123$ .

Software can be asked to produce exact CIs too (jamovi: Fig. 35.9; SPSS: Fig. 35.10). The approximate and exact 95% CIs are very similar.

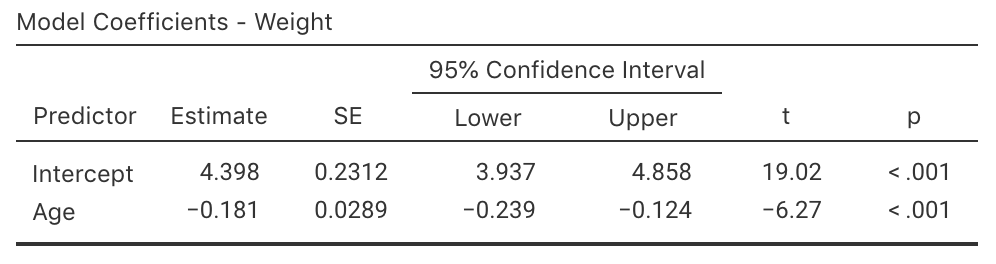
FIGURE 35.9: jamovi output for the red-deer data, including the CIs

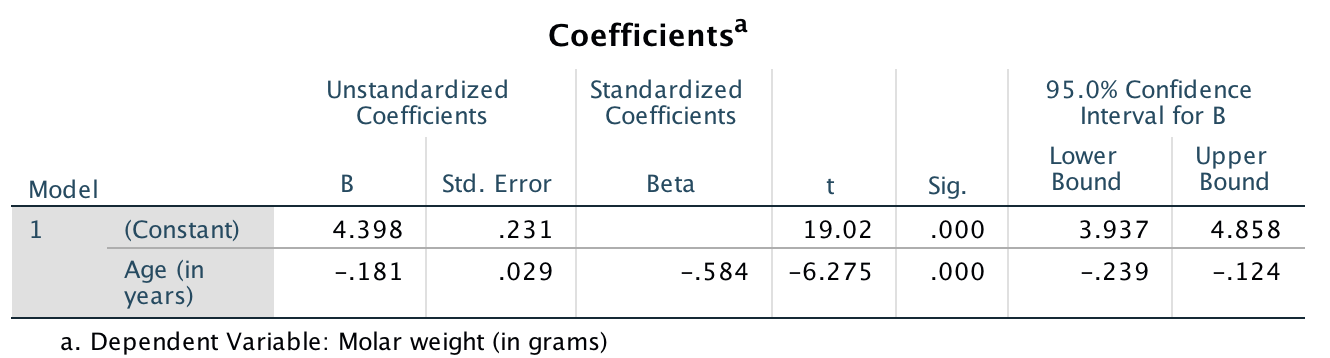
FIGURE 35.10: SPSS output for the red-deer data, including the CIs

We write:

The sample presents very strong evidence ( $P < 0.001$ ; $t = -6.275$ ) of a relationship between age and the weight of molars in male red deer (slope: $-0.181$ ; $n= 78$ ; 95% CI from $-0.239$ to $-0.124$ ) in the population.