30.1 Scaling
“Success is a science; if you have the conditions, you get the result.”
Scaling is a mapping from a variable’s values to how they are represented in a display. The variable to be scaled may be part of the dataset or a statistic calculated from the data, perhaps a count or subgroup means. The mapping is a function for converting the values to the visual properties of the plot, including the limits of the range of data that will be included. The resulting scale is annotated with breaks (tickmarks) and labels to make it more readable. A variable can be transformed and then plotted or the variable can be plotted on a transformed scale.
Scaling sets the limits of a display. Anything outside the limits is not shown. One example is Figure 3.2, which is a histogram of movie lengths of up to 3 hours that excludes the 682 films with longer runtimes. Or limits cover a wider range than the data to provide more space or to include particular standard values. Figure 9.5 is drawn with a scale from 0 to 100% although the maximum upper limit of the confidence intervals is only just over 75%. The reason is to emphasise the full range of possible values and to make clear that most states opposed the measure. It is sometimes suggested that 0 should always be included on count and other scales. This is generally sound advice and is followed, for instance, in the first plot of Figure 21.12. There the intention is to show that the down race is slightly longer than the upper race and that there is variation in the distances up and down over the years, but that these differences are small compared to the overall race length. Using 0 as a baseline would not be as sensible in many of the other plots in Chapter 21. Displays of race times (such as Figures 21.6 and 21.14) and of race speeds (Figure 21.11) are designed to point out the differences in times and speeds, not the overall levels. Figures 21.11 and the left plot of 21.12 are shown again in Figure 30.1.
Figure 30.1: Average speed of the fastest runners (above) and median runners (below) in km/hr for the “up” (dark orange) and “down” (black) races, and distances in km for the “up” and “down” races, all since 1970
Outliers are a problem for scales. A single extreme outlier can stretch the limits and compress the rest of the data into a single, uninformative block (cf. the left plot in Figure 32.10). It will also affect boxplots, scatterplots, and parallel coordinate plots. This only applies to cases that are outliers on individual dimensions. Higher dimensional outliers (for instance, some of the cases revealed in Figure 11.6) do not affect graphics in this way.
Scales are for guidance not precision. Graphics are unsuitable for reading off individual values, although it is useful to know roughly what values apply. This is why the choice of units for scale labels is worth thinking about. The data displayed in Figure 3.1 are recorded in minutes up to 51420, not a number that makes sense to most readers. Converting the scale into weeks makes the plot more understandable with the maximum being just over 5 weeks. Similarly, Figure 10.6 uses a log scale for mission times and adds labels for recognisable lengths of time (hour, day, week) rather than marks equally spaced on the log scale.
Labelled breaks in scales aid understanding and offer points of reference. Too many can lead to crowding or even overplotting and too few do not offer enough assistance. The overall size chosen for a graphic has an influence and it can be curious to see what happens to scale labels when graphics are shrunk.
There are several ways a variable can contribute to a display including horizontal position (x-axis), vertical position (y-axis), pointsize, linewidth, colour, and alpha transparency. Some are easier to assess than others. As Cleveland & McGill (1987) and other research since have pointed out, lengths along a common scale are best for comparison. Pointsize and linewidth are useful for showing large differences, as in Figures 9.12 and 25.12 (pointsize), and Figures 2.10 and 8.9 (linewidth), but not for finer differentiation.
Some attributes have continuous scales, some are categorical, such as shape or linetype. Colour can be continuous (as in Figure 9.4) or discrete (Figure 26.7) or categorical (Figure 4.2). Alpha transparency is a valuable adjunct to colour for emphasising or de-emphasising particular features (e.g., Figure 8.17). The main use of colour is for categorical variables and is the subject of Chapter 29.
There were publications in the past suggesting methods for producing ‘optimal’ continuous scales. These usually produced exact numbers to several decimal places rather than interpretable round numbers. The term ‘pretty’ scales has emerged to describe the latter. There is no such research for categorical scales, although, as covered in Chapter 31, ordering of these scales makes a great deal of difference. When there are too many categories, some kind of aggregation is helpful. This was done in Figures 15.6 and 15.7 collecting the smallest groups into “Other”. Something similar was done in Figure 9.1, combining the oldest age groups into one of over 80.
There can be several scales in the same plot. Figure 8.12 uses two transformed variables (active chess players and grandmasters per million population), a regional colour coding, and pointsize proportional to population.
Context is important for specifying limits and breaks. In Chapter 17 on fuel efficiency of car models sold in the US, the values are reported in miles per gallon, so those have been used. Most other countries use litres per 100 kilometres. ‘Pretty’ scales would differ for the different units with the same data.
Variables representing dates and times bring their own issues. Months are of different lengths (even years are not always the same length). Should scales include Saturdays and Sundays if no data is recorded on those days? Conversely, for Figure 6.3, redrawn as Figure 30.2, missing values were added to the dataset for the Olympic Games that did not take place because of the World Wars. This was to ensure that gaps appeared in the time series to signify what had happened.
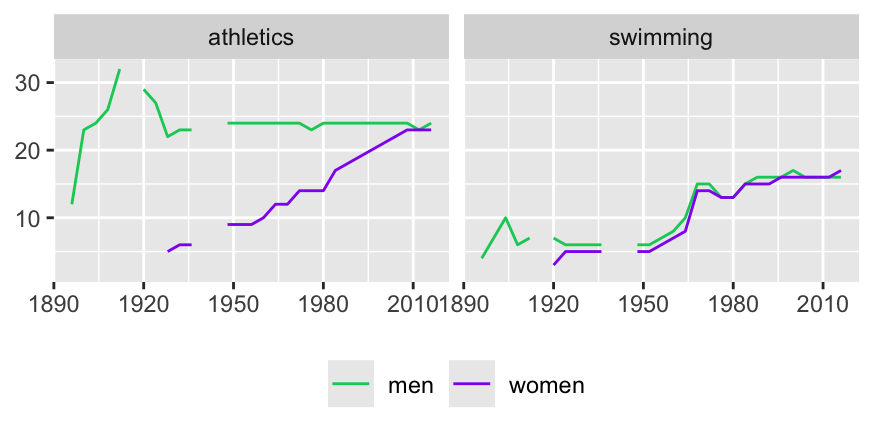
Figure 30.2: Numbers of athletics and swimming events for men and women at the Summer Olympics from 1896 to 2016
If scales are labelled by months, should the label be at the beginning of the month or the middle of the month? Again, much will depend on context. The level of detail of the labelling of time scales is problematic. The timing of the ballots at the Democratic Convention in 1912 was important, as can be seen in Figure 4.7. The times can be read from the dataset. Adding them to the graphic would overload the display and would add information that barely contributes more to what can be seen already.
Scales for spatial data are a quite separate matter. Maps can be drawn using any number of different projections. This does not affect most of Europe much, but has a big effect near the poles. Consider drawing a map of the Palmer Archipelago where the data used in Chapter 18 were studied.
Default scales drawn by software will usually be good for exploratory purposes for individual graphics. They will usually not be as good for comparing graphics. Then common scaling (i.e. using the same scale for comparable axes) will be more suitable. Figure 7.2 is an example where common scaling has been used for three histograms to emphasise the differences in the ranges of numbers of workers. In Figure 7.3 default scales have been used for studying the associations, if any, between the sectors. It is often useful to put vertical count axes on the same scale, as in Figure 23.1 where numbers may be compared across graphics as well as within since the graphics are all of the same dataset. Finally, if related variables are plotted together it makes sense to use a common scale (e.g., for the x and y axes of each plot in Figure 18.11). The default for drawing faceted graphics is common scaling, even if occasionally this is not what is wanted. Graphics are like that, there are always exceptions to any rule.
Common scaling has been used above to refer to using the same scale. It is better to think of it more generally as designing scales that support comparing variables. The transformations used to convert individual event performances in the Decathlon into points are an example (even if they do not work as well as desired, cf. Figure 31.5). Transformations for the axes of parallel coordinate plots are another, although it is more to do with treating variables equally than comparing them: variables can be transformed to [0,1], to z scores, to robust equivalents of z scores, to ranks.
Scales are needed immediately for drawing graphics. They may be amended after seeing the data. Reasons include making more space around the data, including special values, excluding outliers, and supporting comparisons. Overlaying graphical layers may require changes in limits if the range of the initial layer is not wide enough.