5.3 Comparing the data of Michelson and Newcomb
Both researchers made measurements of the speed of light in air, averaged their results, and only then converted their final estimate to one for the speed of light in a vacuum. This meant adding 92 km/s for Michelson (Michelson (1880) p. 141) and 94 km/s for Newcomb (Newcomb (1891) p. 201). The main adjustment was to multiply the speed in air by the index of refraction of air at the temperature of the experiments. The technical details (and much more) are in their papers. Given the adjustments are so similar the estimates for the speed in air can be compared. The extreme outlier in the Newcomb data has been excluded for this comparison, so the horizontal scale is different from the scale of the earlier plots.
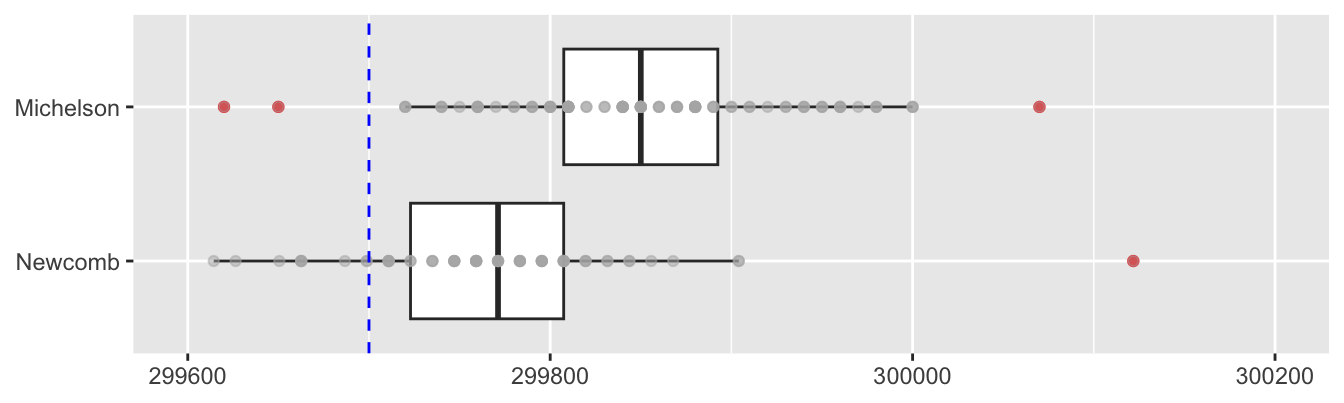
Figure 5.9: Boxplots and dotplots of estimates of the speed of light in air by Michelson in 1879 and by Newcomb in 1882 with the transformed value of today marked by a dashed blue line
Michelson’s estimates were higher than Newcomb’s and further away from the ‘true’ value. In 1924, some forty years later, using similar, but improved techniques, Michelson estimated the speed of light in vacuo to be 299796 km/s (Michelson (1927)), very close to-day’s 299792.458 km/s.
No intervals for the estimates have been given here. As Youden pointed out over 50 years ago (Youden (1972)), reported intervals for estimates of the values of physical constants included random error but not systematic error and that was typically larger.
Answers Newcomb’s estimates were closer to today’s value than Michelson’s. The individual experiments of each of the two researchers can only approximately be treated as independent random samples.
Further questions How have experiments to estimate the speed of light changed since Newcomb’s time? How have the estimates themselves changed?