\( \newcommand{\bm}[1]{\boldsymbol{#1}} \newcommand{\textm}[1]{\textsf{#1}} \newcommand{\textnormal}[1]{\textsf{#1}} \def\T{{\mkern-2mu\raise-1mu\mathsf{T}}} \newcommand{\R}{\mathbb{R}} % real numbers \newcommand{\E}{{\rm I\kern-.2em E}} \newcommand{\w}{\bm{w}} % bold w \newcommand{\bmu}{\bm{\mu}} % bold mu \newcommand{\bSigma}{\bm{\Sigma}} % bold mu \newcommand{\bigO}{O} %\mathcal{O} \renewcommand{\d}[1]{\operatorname{d}\!{#1}} \)

11.2 From Dollar to Risk Diversification

Risk parity is an approach to investment management that focuses on allocation of risk rather than allocation of dollars or capital. In other words, it departs from the concept of dollar diversification to risk diversification. The underlying idea is to design the asset allocation so that each asset (or asset class) contributes the same risk level to the overall portfolio. This typically produces better out-of-sample risk control and can be more resistant to market downturns than traditional portfolios.

Historically, risk parity starts from the observation that traditional asset allocations, such as the market portfolio or the 60/40 portfolio in stocks/bonds, are insufficiently diversified in terms of risk contribution (Asness et al., 2012). From a risk perspective, the 60/40 portfolio is mainly equity portfolio since stocks are much more volatile than bonds and dominate the risk of the entire portfolio.

Some of the theoretical components were developed in the 1950s and 1960s, but the first risk parity fund, called the “All Weather” fund, was pioneered by Bridgewater Associates in 1996. An early analysis in terms of partial derivatives to identify “hot spots” can be found in Litterman (1996). The term “risk parity” was coined in 2005 by Edward Qian50 (Qian, 2005) and, in recent years, it has been adopted by the asset management industry as a way of risk management. Risk parity gained significantly in popularity after the global financial crisis in 2008 (Asness et al., 2012; Maillard et al., 2010). Nevertheless, some portfolio managers have expressed skepticism about its practical application and effectiveness in all types of market conditions, especially bull markets (R. M. Anderson et al., 2012; Chaves et al., 2011).

The risk parity portfolio has received significant attention from both practitioner and academic communities, producing a large number of publications and some textbooks such as Qian (2016) for a high-level and practical perspective and Roncalli (2013b) for a more mathematical treatment.

Figure 11.1 illustrates the difference between dollar diversification and risk diversification. The \(1/N\) portfolio by definition perfectly diversifies the capital allocation (i.e., portfolio weights) but does not show a good risk diversification profile (in fact, a single asset exhibits a high risk contribution). On the other hand, the risk parity portfolio precisely focuses on the diversification of the risk profile.

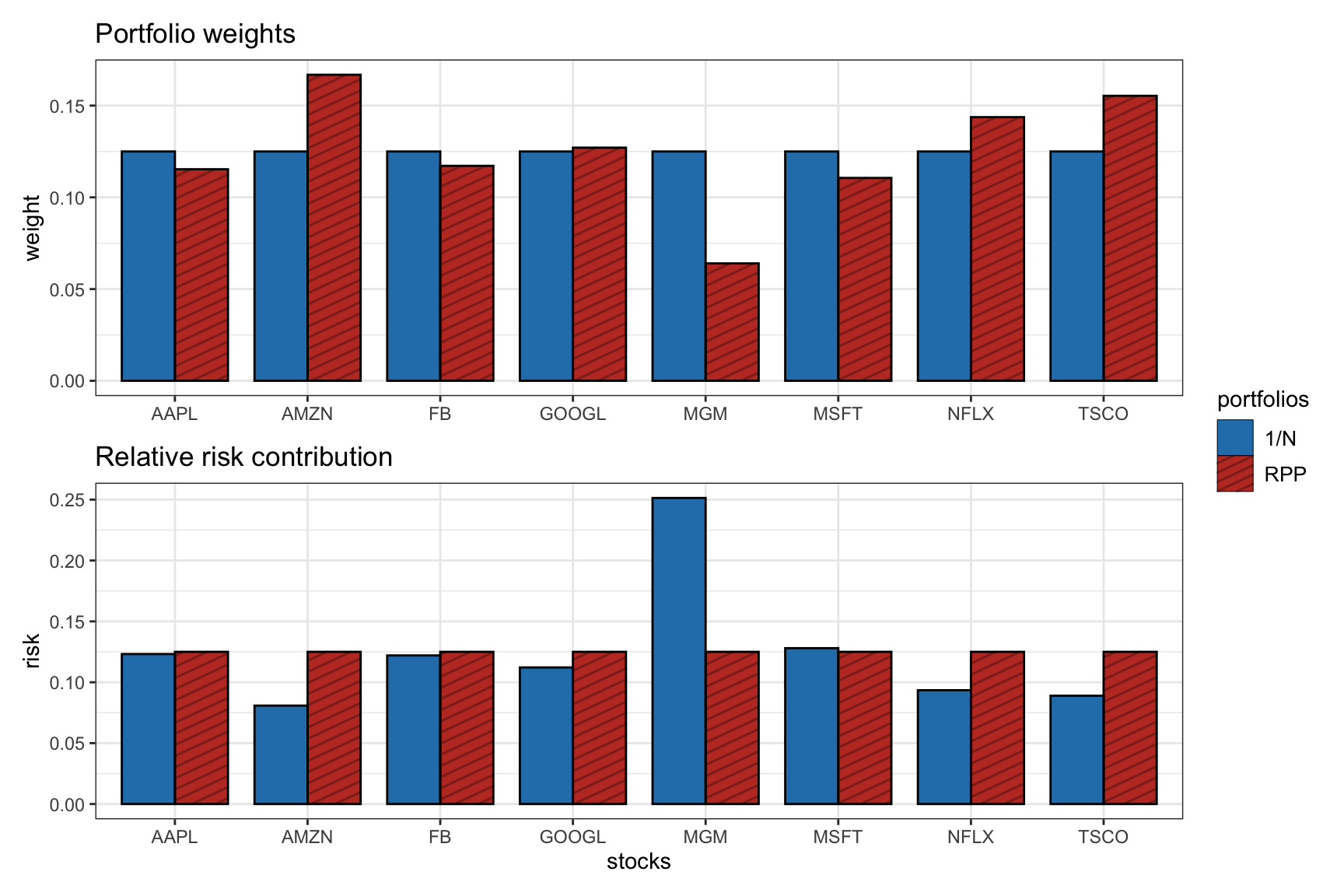
Illustration of portfolio allocation and risk allocation for the $1/N$ portfolio and risk parity portfolio.

Figure 11.1: Illustration of portfolio allocation and risk allocation for the \(1/N\) portfolio and risk parity portfolio.

References

Anderson, R. M., Bianchi, S. W., and Goldberg, L. R. (2012). Will my risk parity strategy outperform? Financial Analysts Journal, 68(6), 75–93.
Asness, C. S., Frazzini, A., and Pedersen, L. H. (2012). Leverage aversion and risk parity. Financial Analysts Journal, 68(1), 47–59.
Chaves, D. B., Hsu, J. C., Li, F., and Shakernia, O. (2011). Risk parity portfolio vs. Other asset allocation heuristic portfolios. Journal of Investing, 20(1), 108–118.
Litterman, R. (1996). Hot spots and hedges. Journal of Portfolio Management, 22, 52–75.
Maillard, S., Roncalli, T., and Teiletche, J. (2010). The properties of equally weighted risk contribution portfolios. Journal of Portfolio Management, 36(4), 60–70.
Qian, E. (2005). Risk parity portfolios: Efficient portfolios through true diversification. PanAgora Asset Management.
Qian, E. (2016). Risk Parity Fundamentals. CRC Press.
Roncalli, T. (2013b). Introduction to Risk Parity and Budgeting. Chapman & Hall/CRC.

  1. Dr. Edward Qian is the Chief Investment Officer and Head of Research of the Multi Asset Group at PanAgora Asset Management.↩︎