第 48 章 模拟与抽样1

library(tidyverse)

本章目的是在tidyverse的架构下，介绍一些模拟和抽样的知识。先回顾下Hadley Wickham提出的数据科学tidy原则，tidy思想体现在:

• 任何数据都可以规整为数据框
• 数据框的一列代表一个变量，数据框的一行代表一次观察
• 函数处理数据时，数据框进、数据框出

48.1 模拟

48.1.1 生成随机数

比如生成5个高斯分布的随机数，高斯分布就是正态分布，R语言里我们用rnorm()函数产生正态分布的随机数

rnorm(n = 5, mean = 0, sd = 1)

## [1] -2.0274777  1.1326289  0.1618004 -1.8634953 -1.4794975

事实上，R内置了很多随机数产生的函数

Distrution	Notation	R
Uniform	\(\text{U}(a, b)\)	runif
Normal	\(\text{N}(\mu, \sigma)\)	rnorm
Binormal	\(\text{Bin}(n, p)\)	rbinorm
Piosson	\(\text{pois}(\lambda)\)	rpois
Beta	\(\text{Beta}(\alpha, \beta)\)	rbeta

如果大家查看帮助文档?runif，会发现每种分布都有对应的四个函数

• d:density
• p:cumulative probability
• q:quantile
• r:random

dnorm(seq(0.1, 0.5, length.out = 10), mean = 0, sd = 1)

##  [1] 0.3969525 0.3948021 0.3918885 0.3882287 0.3838441 0.3787602 0.3730060
##  [8] 0.3666144 0.3596212 0.3520653

在tidyverse的框架下，我们喜欢在数据框(data.frame)下运用这些函数，因为这样我们可以方便使用ggplot2来可视化，

• 例子1，我们生成100个正态分布的点，然后看看其分布

tibble(
  x = rnorm(n = 100, mean = 0, sd = 1)
) %>%
  ggplot(aes(x = x)) +
  geom_density()

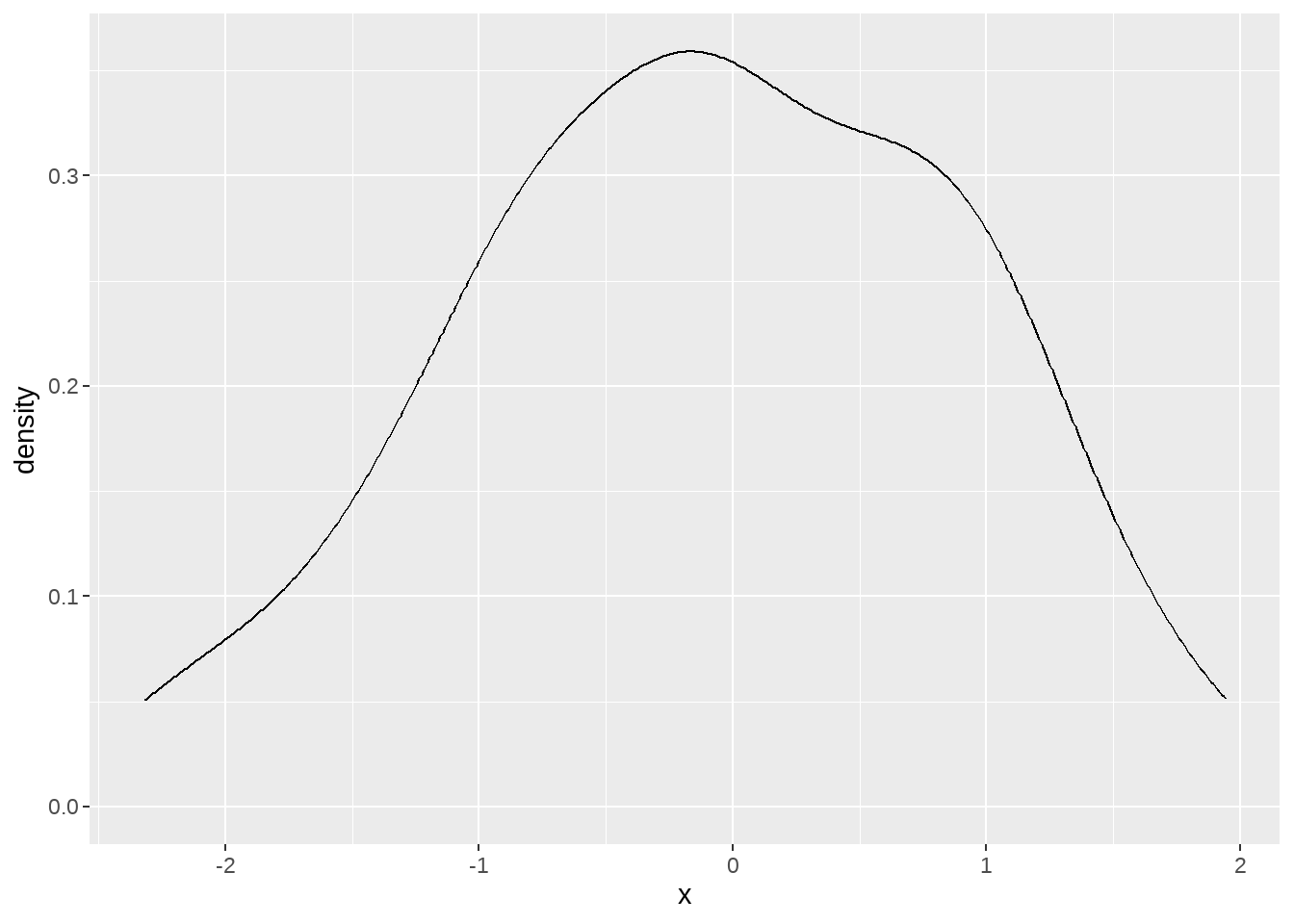
我们将模拟的正态分布和理论上正态分布画在一起

tibble(
  x = rnorm(n = 100, mean = 0, sd = 1)
) %>%
  ggplot(aes(x = x)) +
  geom_density() +
  stat_function(
    fun = dnorm,
    args = list(mean = 0, sd = 1),
    color = "red"
  )

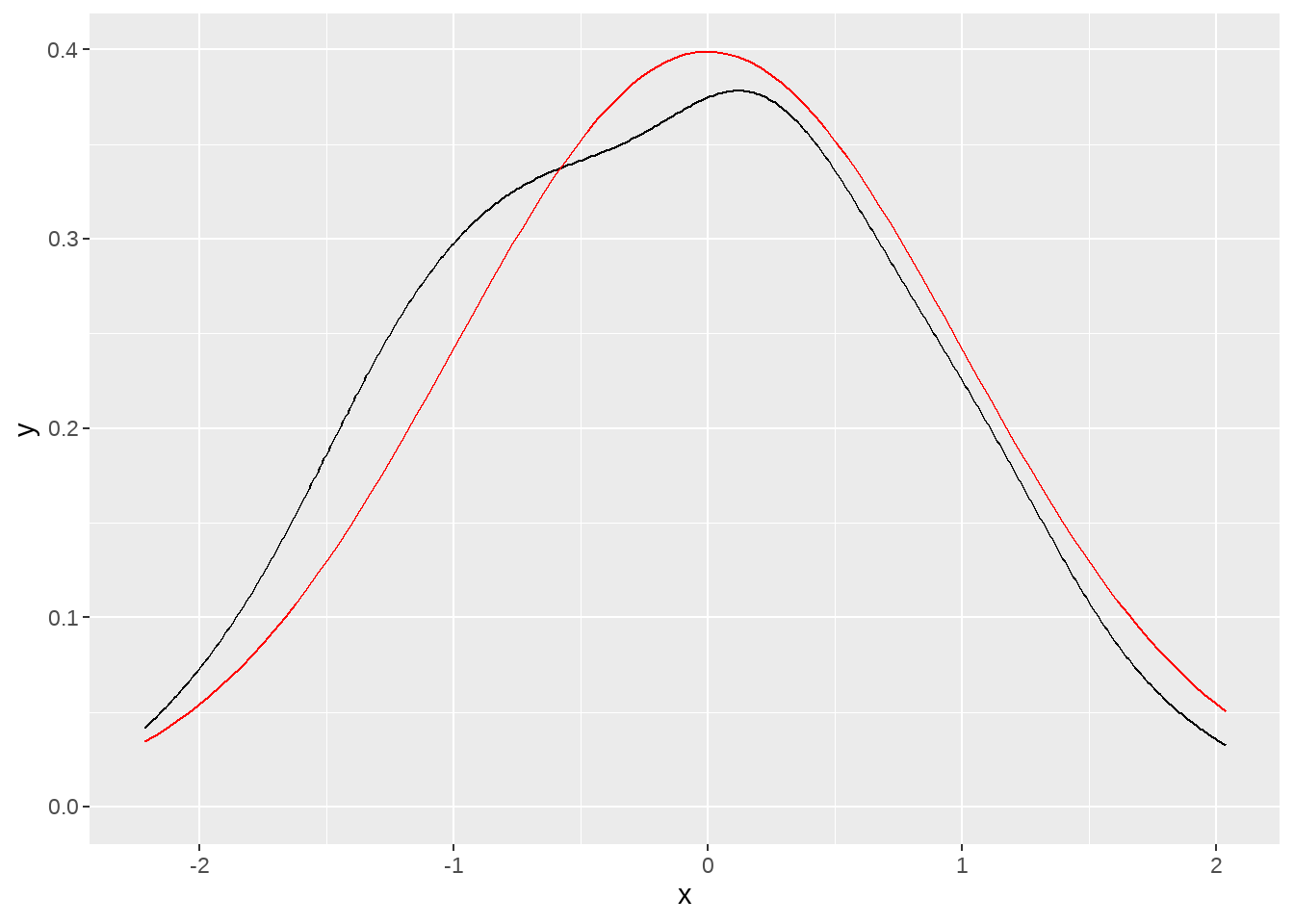
如果我们模拟点再增加点，会越来越逼近理论上的分布。

• 例子2，在数据框(data.frame)下，建立模拟\(x\)和\(y\)的线性关系

\[ y_i = 4 + 3.2\, x_i\] 现实中，观察值往往会带入误差，假定误差服从正态分布，那么\(x\)和\(y\)的线性关系重新表述为 \[ y_i = \beta_0 + \beta_1\, x_i + \epsilon_i, \quad \epsilon \in \text{Normal}(\mu =0, \sigma =1) \]

beta_0 <- 4
beta_1 <- 3.2
epsilon <- rnorm(n = 1000, mean = 0, sd = 1)

sim_normal <- tibble(
  # x_vals = runif(1000, 0, 10)
  x_vals = seq(from = 0, to = 5, length.out = 1000),
  y_vals = beta_0 + beta_1 * x_vals + epsilon,
)

sim_normal %>% head()

## # A tibble: 6 × 2
##    x_vals y_vals
##     <dbl>  <dbl>
## 1 0         2.34
## 2 0.00501   2.35
## 3 0.0100    3.53
## 4 0.0150    2.75
## 5 0.0200    3.68
## 6 0.0250    4.90

sim_normal %>%
  ggplot(aes(x = x_vals, y = y_vals)) +
  geom_point()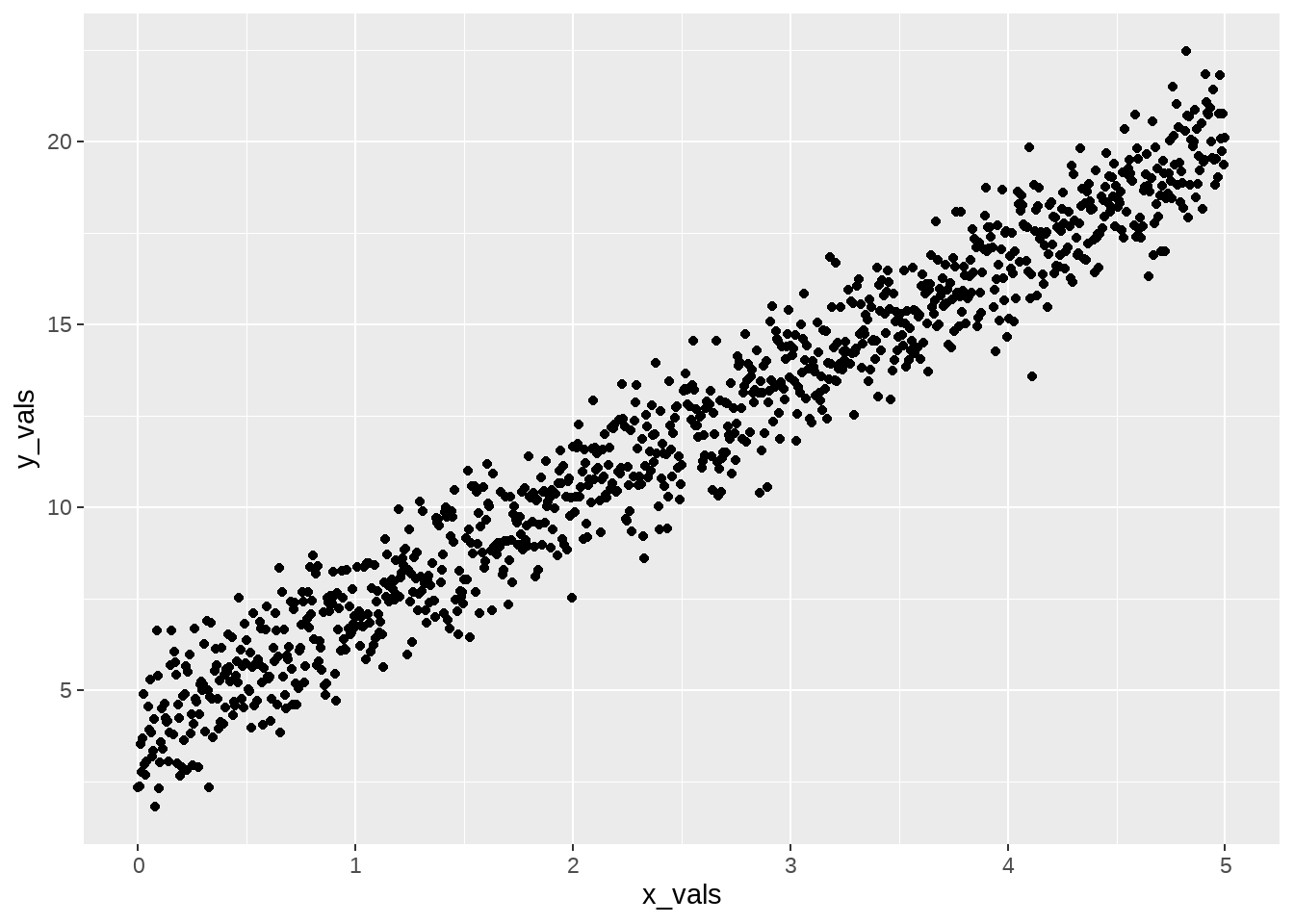

有时候为了方便，可以写简练点

tibble(
  a = runif(1000, 0, 5),
  b = 4 + rnorm(1000, mean = 3.2 * a, sd = 1)
) %>%
  ggplot(aes(x = a, y = b)) +
  geom_point()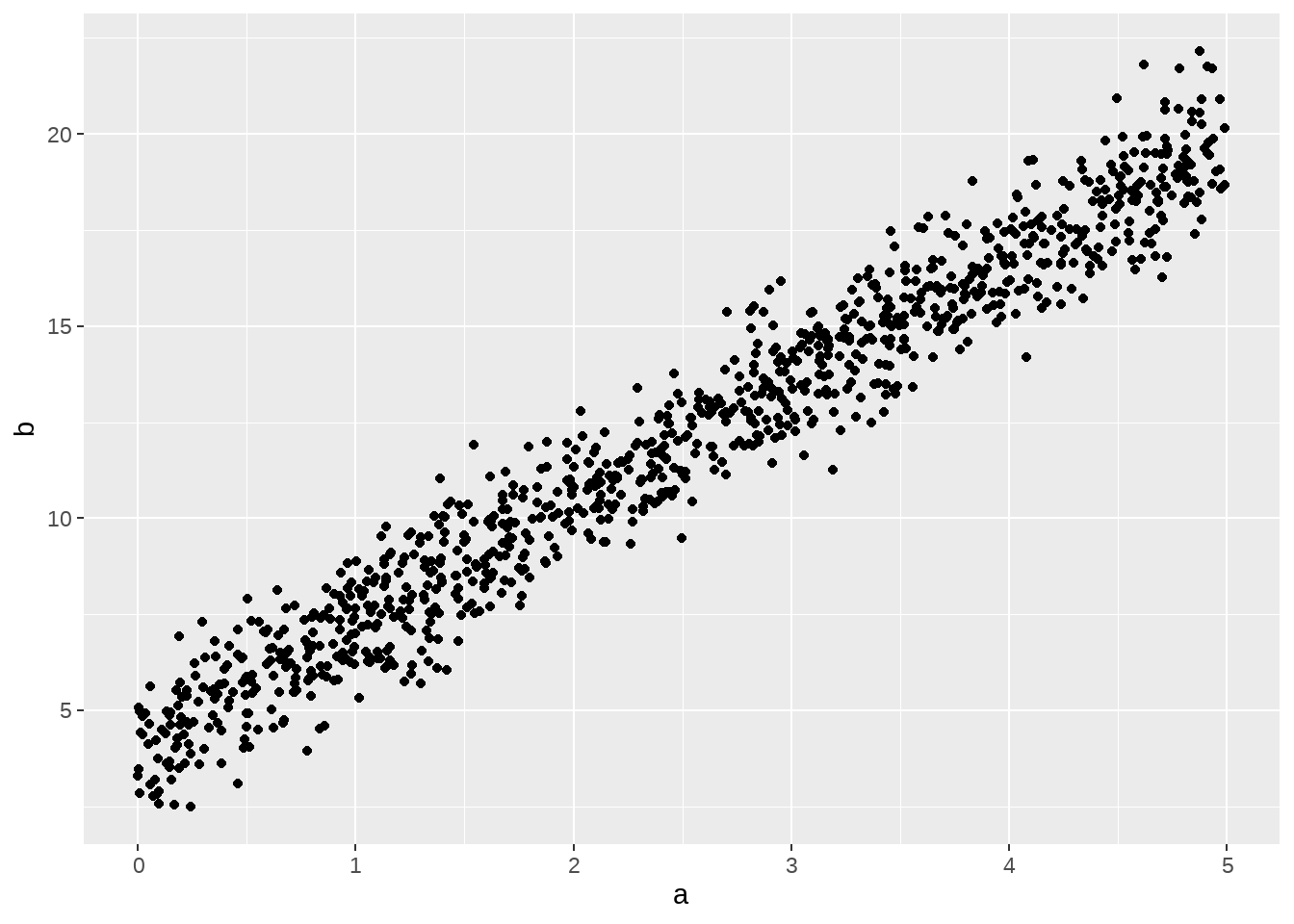

48.2 MASS::mvrnorm

MASS::mvrnorm(n = 1, mu, Sigma)产生多元高斯分布的随机数，每组随机变量高度相关。 比如人的身高服从正态分布，人的体重也服从正态分布，同时身高和体重又存在强烈的关联。

• n: 随机样本的大小
• mu: 多元高斯分布的均值向量
• Sigma: 协方差矩阵，主要这里是大写的S (Sigma)，提醒我们它是一个矩阵，不是一个数值

a <- 3.5
b <- -1
sigma_a <- 1
sigma_b <- 0.5
rho <- -0.7

mu <- c(a, b)
cov_ab <- sigma_a * sigma_b * rho # covariance

构建协方差矩阵

sigma <- matrix(c(
  sigma_a^2, cov_ab,
  cov_ab, sigma_b^2
), ncol = 2)

d <- MASS::mvrnorm(1000, mu = mu, Sigma = sigma) %>%
  data.frame() %>%
  set_names("group_a", "group_b")

head(d)

##    group_a    group_b
## 1 2.731311 -1.0871303
## 2 3.345291 -1.1293124
## 3 3.237802 -0.9686255
## 4 4.296438 -1.1571522
## 5 3.547076 -1.2832276
## 6 3.124146 -1.0497191

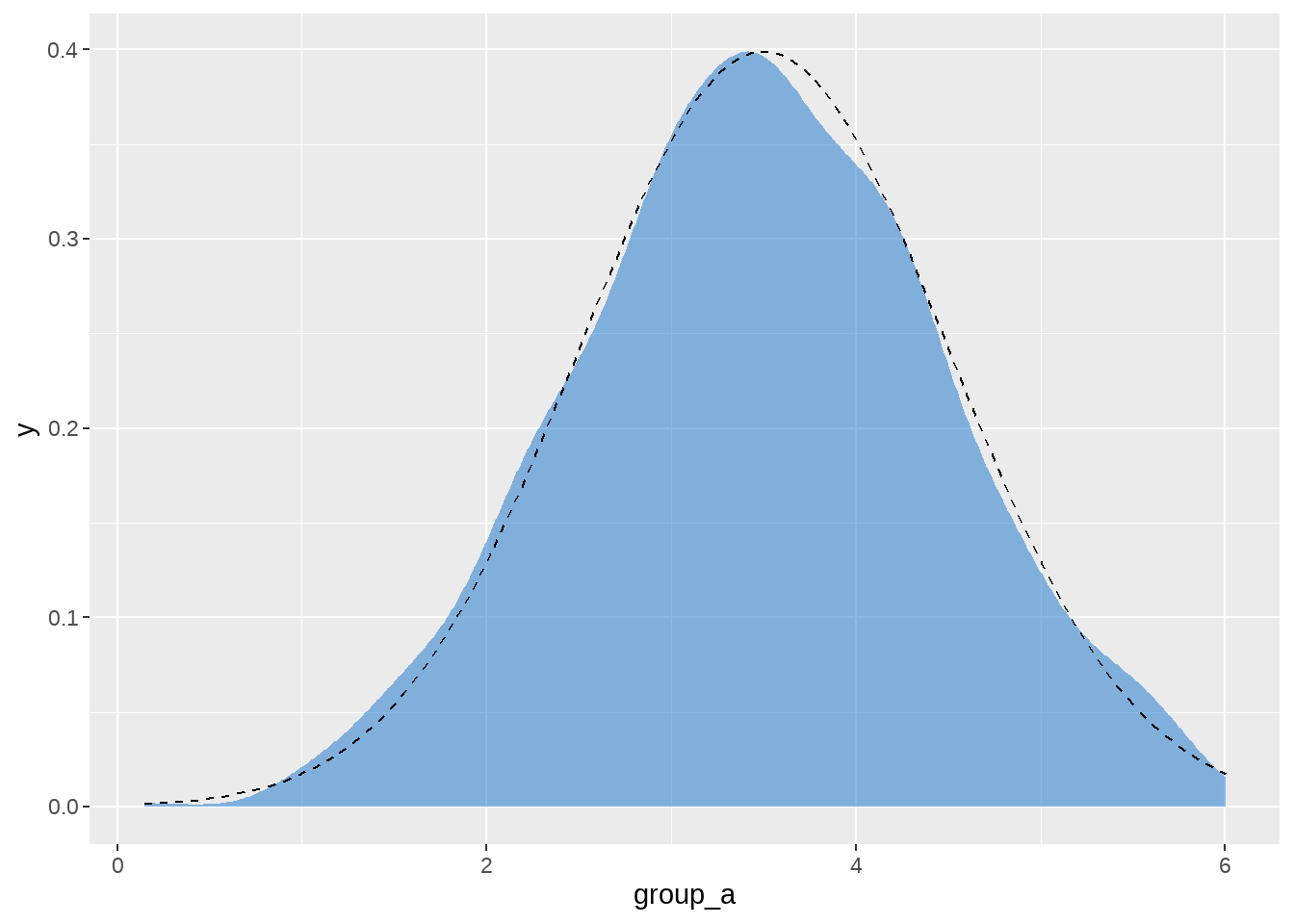
d %>%
  ggplot(aes(x = group_a)) +
  geom_density(
    color = "transparent",
    fill = "dodgerblue3",
    alpha = 1 / 2
  ) +
  stat_function(
    fun = dnorm,
    args = list(mean = 3.5, sd = 1),
    linetype = 2
  )

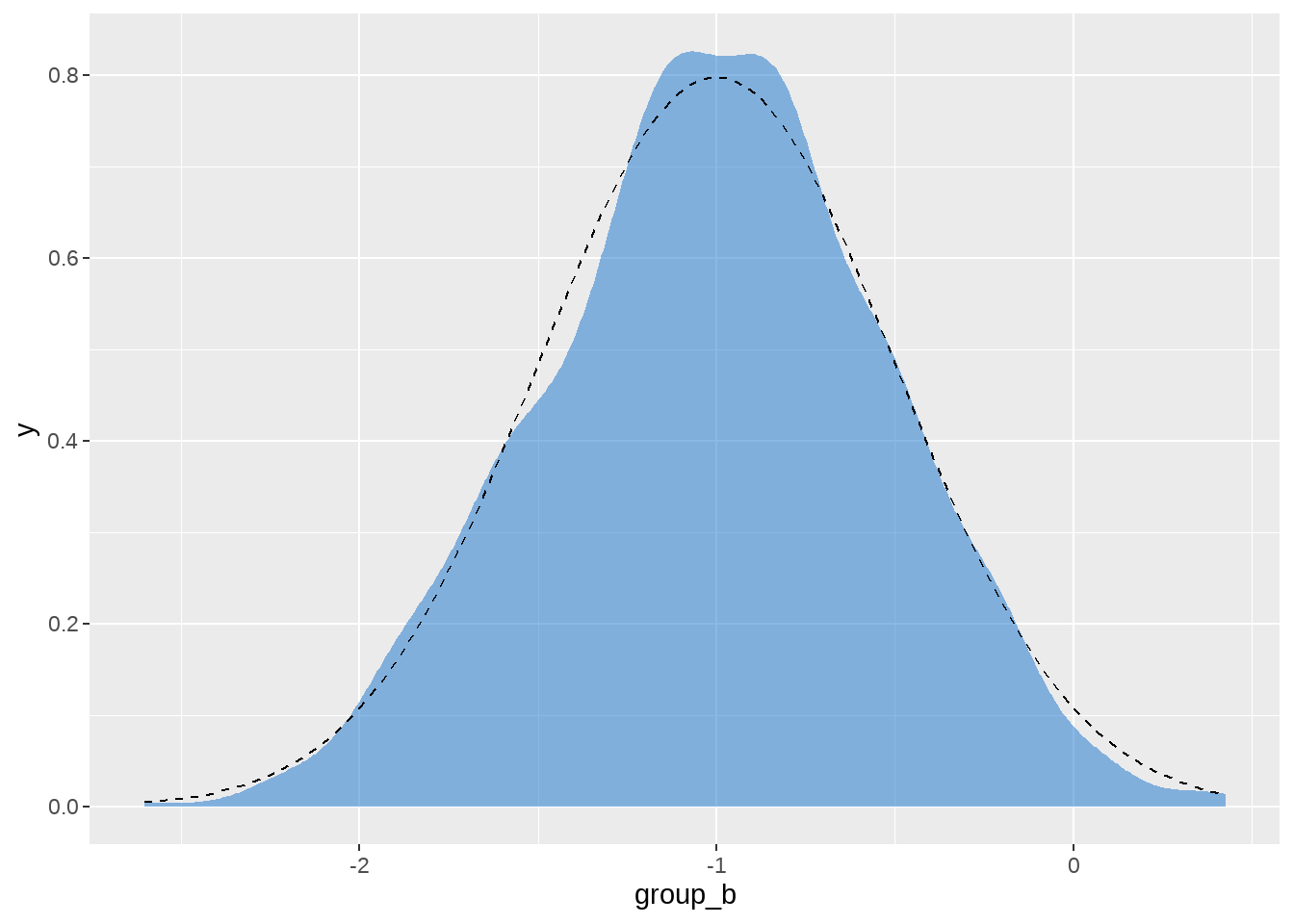
d %>%
  ggplot(aes(x = group_b)) +
  geom_density(
    color = "transparent",
    fill = "dodgerblue3",
    alpha = 1 / 2
  ) +
  stat_function(
    fun = dnorm,
    args = list(mean = -1, sd = 0.5),
    linetype = 2
  )

d %>%
  ggplot(aes(x = group_a, y = group_b)) +
  geom_point() +
  stat_ellipse(type = "norm", level = 0.95)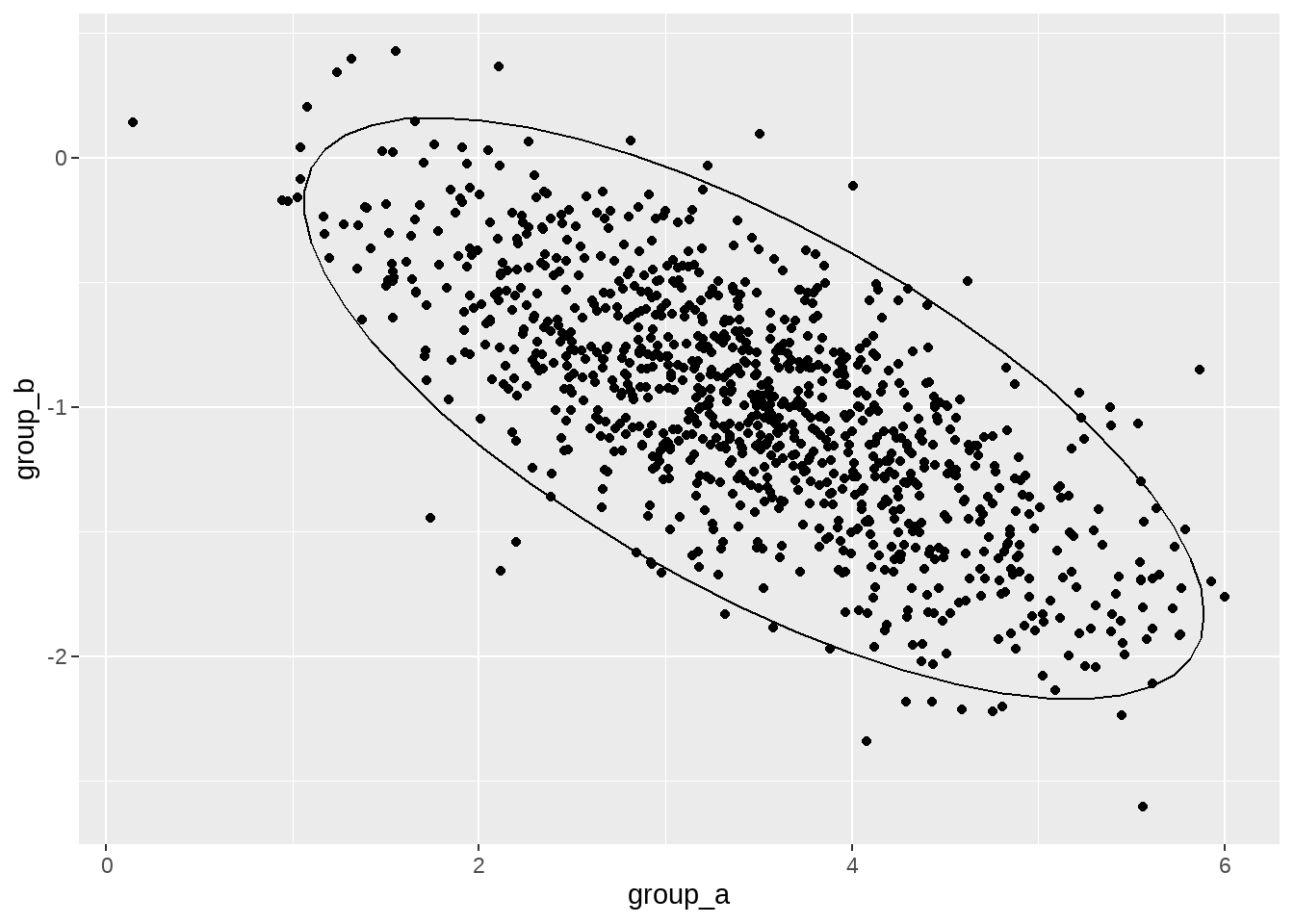

我们回头验算一下

d %>% summarise(
  a_mean = mean(group_a),
  b_mean = mean(group_b),
  a_sd = sd(group_a),
  b_sd = sd(group_b),
  cor = cor(group_a, group_b),
  cov = cov(group_a, group_b)
)

##     a_mean    b_mean      a_sd      b_sd        cor        cov
## 1 3.474021 -1.004222 0.9849412 0.4757985 -0.7092452 -0.3323761

48.3 蒙特卡洛

这是我研究生时候老师布置的一个的题目，当时我用的是C语言代码，现在我们有强大的tidyverse

set.seed(2019)

n <- 50000
points <- tibble("x" = runif(n), "y" = runif(n))

points <- points %>%
  mutate(inside = map2_dbl(.x = x, .y = y, ~ if_else(.x**2 + .y**2 < 1, 1, 0))) %>%
  rowid_to_column("N")

正方形的面积是1，圆的面积是\(\pi r^2 = \frac{1}{4} \pi\)，如果知道两者的比例，就可以估算\(\pi\)

points <- points %>%
  mutate(estimate = 4 * cumsum(inside) / N)

points %>% tail()

## # A tibble: 6 × 5
##       N       x      y inside estimate
##   <int>   <dbl>  <dbl>  <dbl>    <dbl>
## 1 49995 0.591   0.0411      1     3.15
## 2 49996 0.945   0.127       1     3.15
## 3 49997 0.654   0.159       1     3.15
## 4 49998 0.521   0.491       1     3.15
## 5 49999 0.812   0.203       1     3.15
## 6 50000 0.00935 0.657       1     3.15

points %>%
  ggplot() +
  geom_line(aes(y = estimate, x = N), colour = "#82518c") +
  geom_hline(yintercept = pi)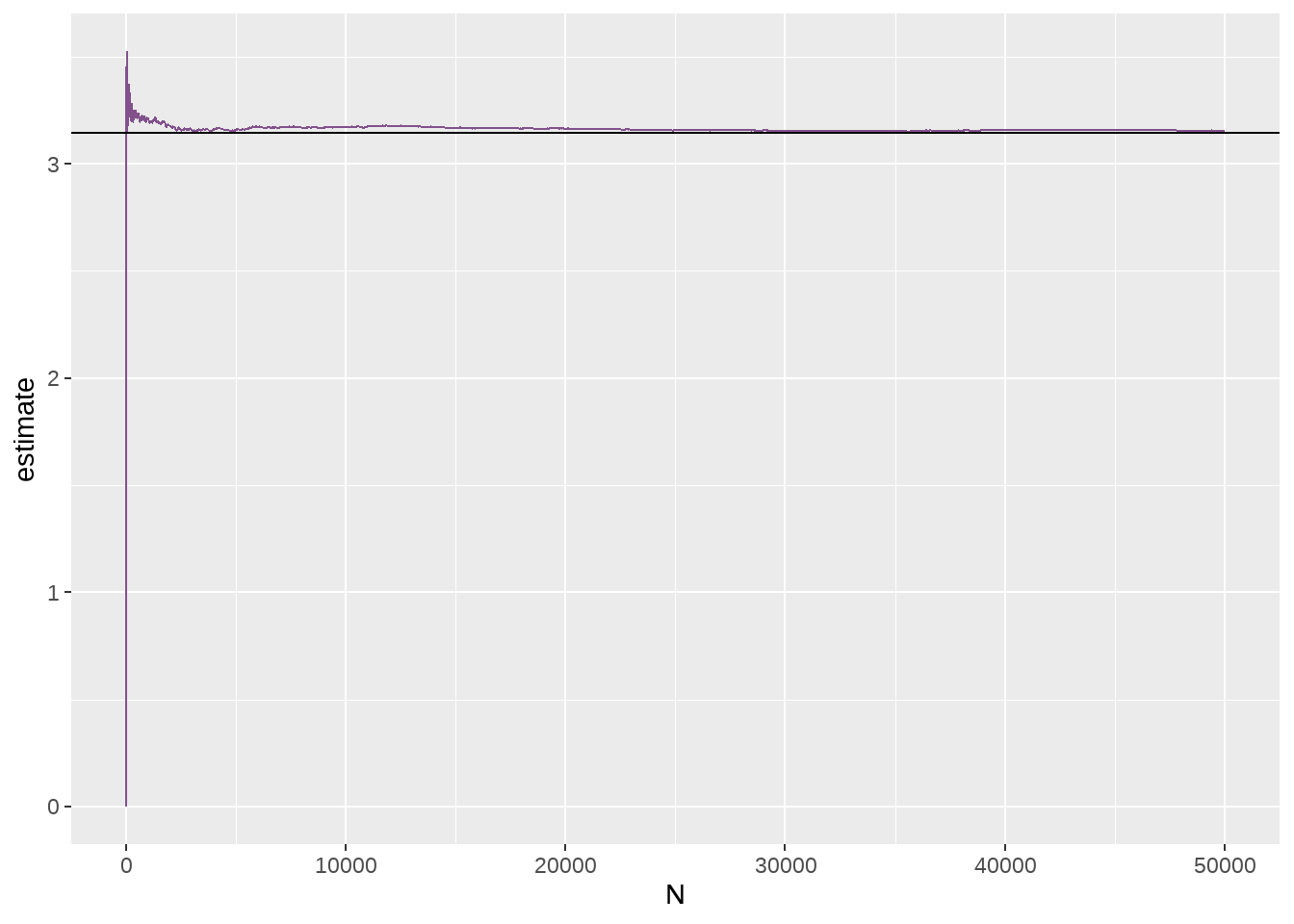

48.4 抽样与样本

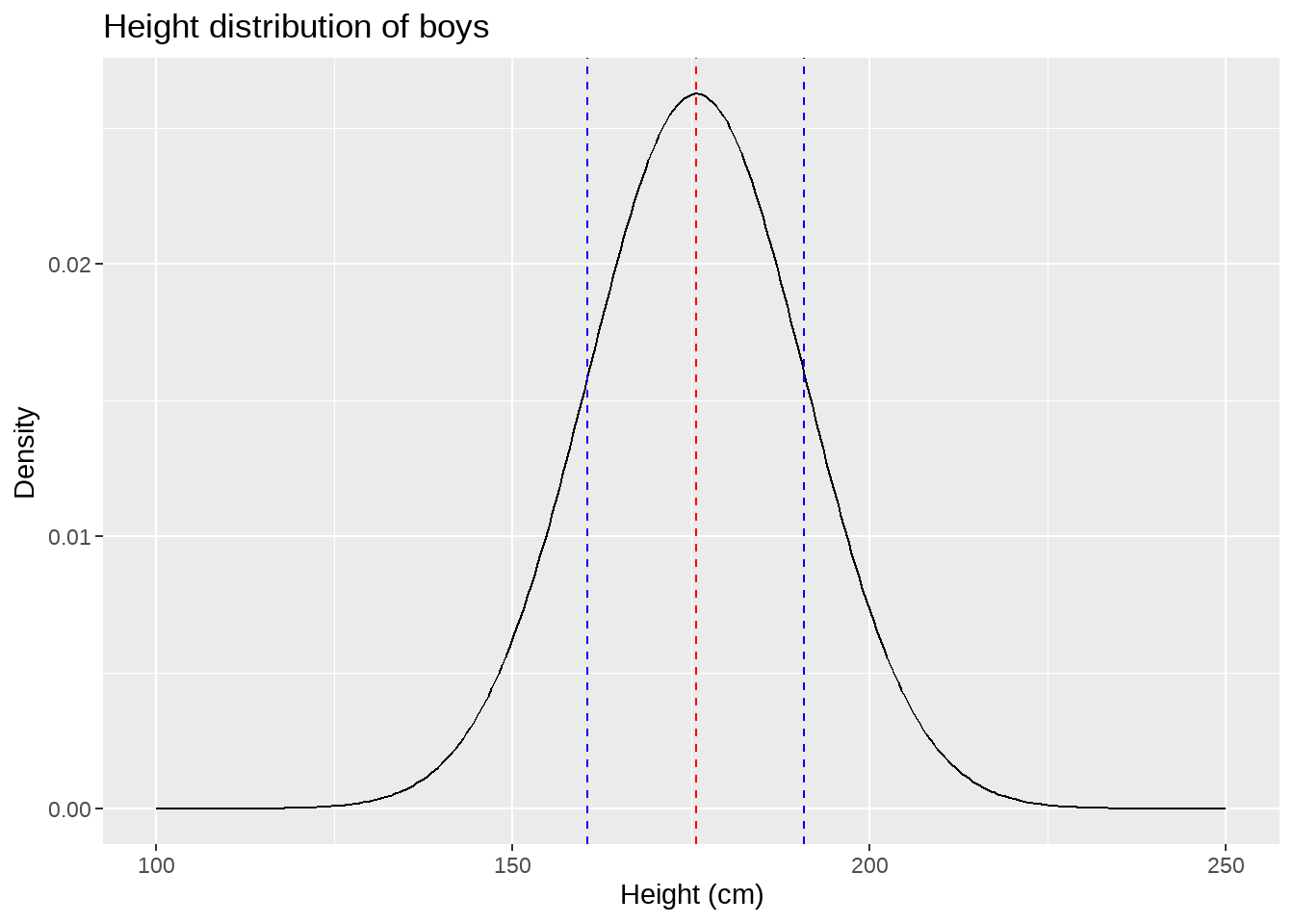
48.4.1 总体分布

假定一个事实，川师男生总体的平均身高和身高的标准差分别为

true.mean <- 175.7
true.sd <- 15.19

那么我们可以模拟分布情况如下

pop.distn <-
  tibble(
    height = seq(100, 250, 0.5),
    density = dnorm(height, mean = true.mean, sd = true.sd)
  )

ggplot(pop.distn) +
  geom_line(aes(height, density)) +
  geom_vline(
    xintercept = true.mean,
    color = "red",
    linetype = "dashed"
  ) +
  geom_vline(
    xintercept = true.mean + true.sd,
    color = "blue",
    linetype = "dashed"
  ) +
  geom_vline(
    xintercept = true.mean - true.sd,
    color = "blue",
    linetype = "dashed"
  ) +
  labs(
    x = "Height (cm)", y = "Density",
    title = "Height distribution of boys"
  )

48.4.2 样本

假定我们从中抽取30个男生身高样本

sample.a <-
  tibble(height = rnorm(n = 30, mean = true.mean, sd = true.sd))

然后看看样本的直方图

sample.a %>%
  ggplot(aes(x = height)) +
  geom_histogram(aes(y = stat(density)),
    fill = "steelblue",
    alpha = 0.75,
    bins = 10
  ) +
  geom_line(
    data = pop.distn,
    aes(x = height, y = density),
    alpha = 0.25, size = 1.5
  ) +
  geom_vline(xintercept = true.mean, linetype = "dashed", color = "red") +
  geom_vline(xintercept = mean(sample.a$height), linetype = "solid")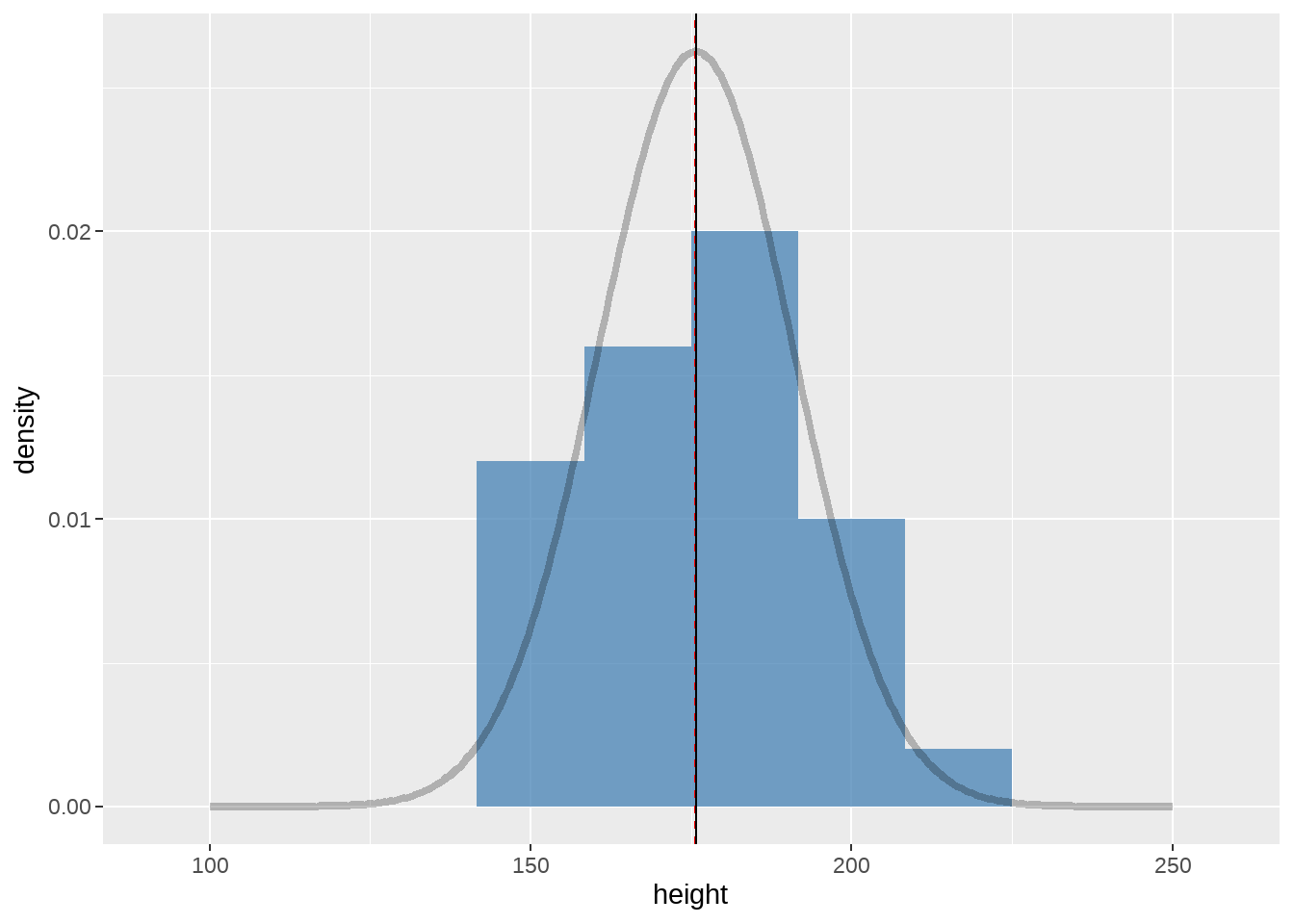

红色的虚线代表分布的总体的均值，黑色实线代表30个样本的均值，

sample.a %>%
  summarize(
    sample.mean = mean(height),
    sample.sd = sd(height)
  )

## # A tibble: 1 × 2
##   sample.mean sample.sd
##         <dbl>     <dbl>
## 1        176.      17.3

也就是说，基于这30个观察值的样本，我们认为川师男生的身高均值为175.7429846cm，方差为17.3026755

可能有同学说，这个样本太少了，计算的均值还不够科学，会以偏概全。于是又重新找了30个男生，和上次类似，用rnorm函数模拟，我们记为样本b

sample.b <-
  tibble(height = rnorm(30, mean = true.mean, sd = true.sd))

再来看看这次样本的分布

sample.b %>%
  ggplot(aes(x = height)) +
  geom_histogram(aes(y = stat(density)),
    fill = "steelblue", alpha = 0.75, bins = 10
  ) +
  geom_line(
    data = pop.distn, aes(x = height, y = density),
    alpha = 0.25, size = 1.5
  ) +
  geom_vline(xintercept = true.mean, linetype = "dashed", color = "red") +
  geom_vline(xintercept = mean(sample.a$height), linetype = "solid")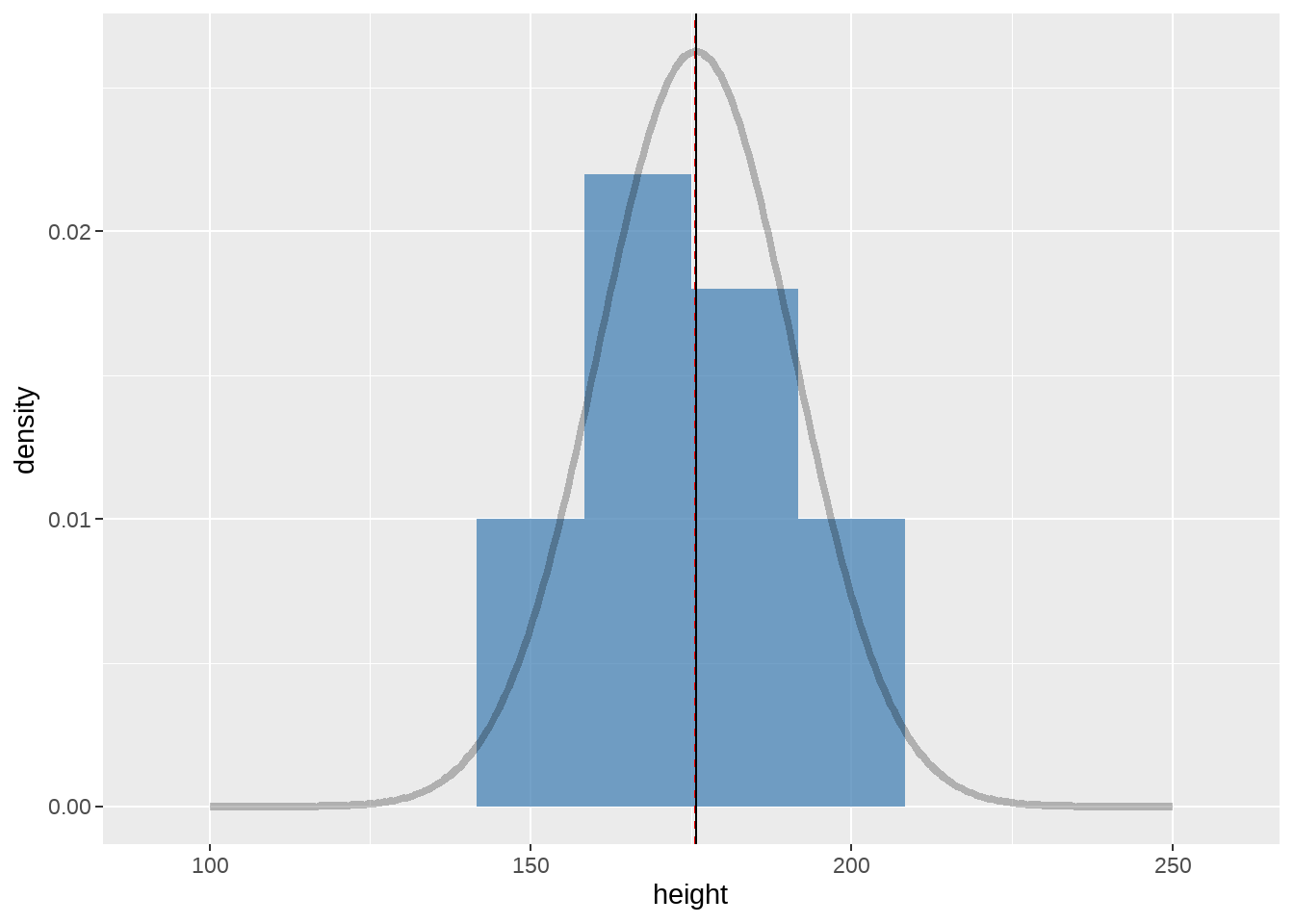

同样，我们计算样本b的均值和方差

sample.b %>%
  summarize(
    sample.mean = mean(height),
    sample.sd = sd(height)
  )

## # A tibble: 1 × 2
##   sample.mean sample.sd
##         <dbl>     <dbl>
## 1        174.      14.9

这次抽样的结果，均值为173.711025cm，方差为14.864061

和样本a比，有一点点变化。不经想问，我能否继续抽样呢？结果会有变化吗？为了避免重复写代码 ，我把上面的过程整合到一起，写一个子函数，专门模拟抽样过程

rnorm.stats <- function(n, mu, sigma) {
  the.sample <- rnorm(n, mu, sigma)
  tibble(
    sample.size = n,
    sample.mean = mean(the.sample),
    sample.sd = sd(the.sample)
  )
}

于是，我们又可以继续模拟了。注意我们之前设定的总体分布的均值和方差

true.mean <- 175.7
true.sd <- 15.19

rnorm.stats(30, true.mean, true.sd)

## # A tibble: 1 × 3
##   sample.size sample.mean sample.sd
##         <dbl>       <dbl>     <dbl>
## 1          30        175.      16.2

yes，代码工作的很好，但不过只是代码减少了一点点，仍然只是一次抽样（这里30个样本为一次抽样），我们的目的是反复抽样， 抽很多次的那种喔。

那我们用purrr包的rerun函数偷个懒，

df.samples.of.30 <-
  purrr::rerun(2500, rnorm.stats(30, true.mean, true.sd)) %>%
  dplyr::bind_rows()

哇，一下子抽了2500个样本,全部装进了df.sample.of.30这个数据框， 偷偷看一眼呢

df.samples.of.30 %>% head()

## # A tibble: 6 × 3
##   sample.size sample.mean sample.sd
##         <dbl>       <dbl>     <dbl>
## 1          30        173.      16.1
## 2          30        178.      15.8
## 3          30        175.      14.2
## 4          30        179.      17.9
## 5          30        178.      15.4
## 6          30        180.      12.6

回过头看看df.samples.of.30是什么：

• 从川师的男生中随机抽取30个，计算这30个人身高的均值和方差，这叫一次抽样
• 把上面的工作，重复2500次，得到2500个均值和方差
• 2500个均值和方差，组成了一个数据框

我们发现每次抽样的均值都不一样，感觉又像一个分布(抽样的均值分布)，我们画出来看看吧

df.samples.of.30 %>%
  ggplot(aes(x = sample.mean, y = stat(density))) +
  geom_histogram(bins = 25, fill = "firebrick", alpha = 0.5) +
  geom_vline(xintercept = true.mean, linetype = "dashed", color = "red") +
  labs(
    title = "Distribution of mean heights for 2500 samples of size 30"
  )

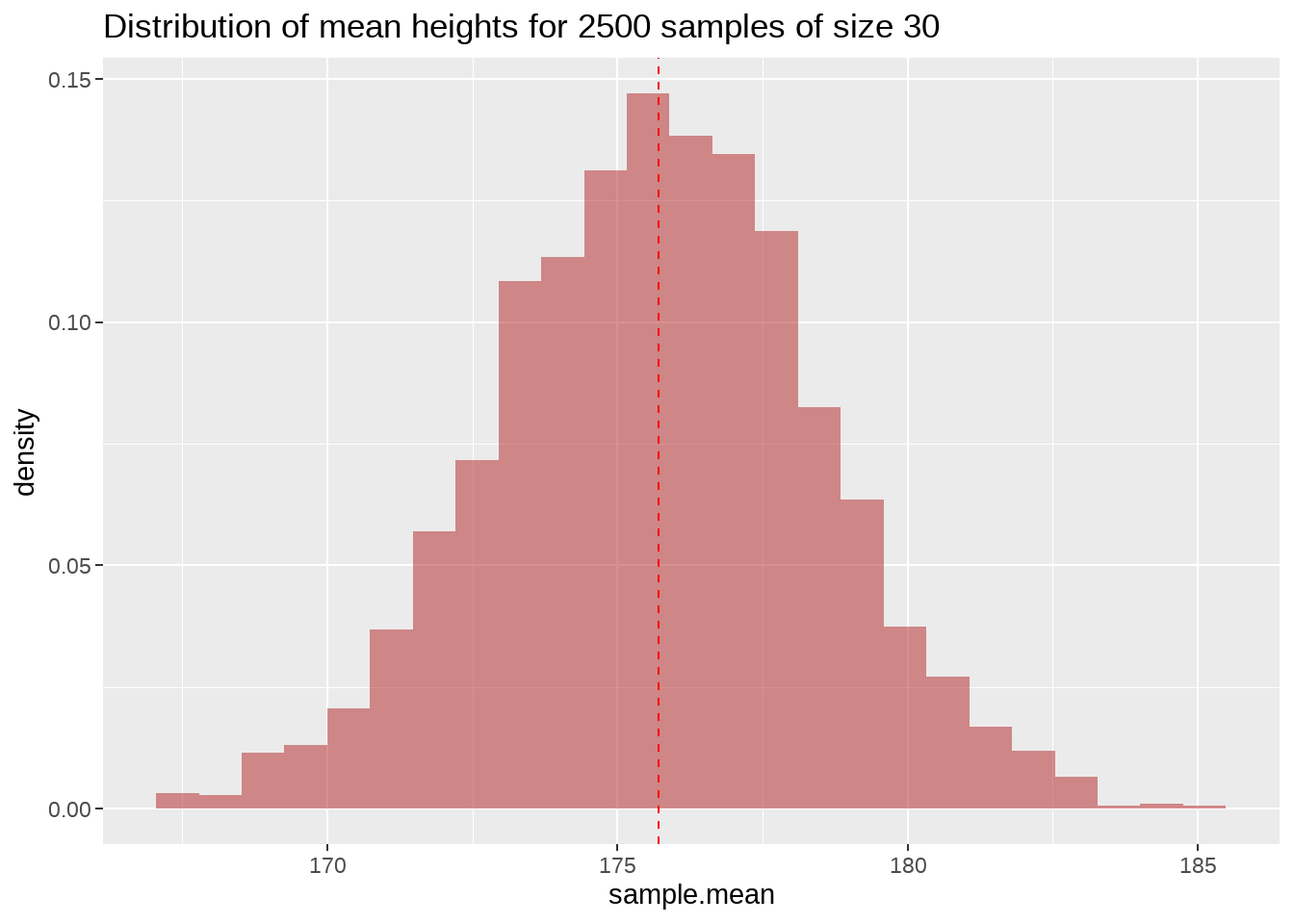
注意到，这不是男生身高的分布，而是每次抽样计算的均值构成的分布.

为了更清楚的说明，我们把整体的分布(灰色曲线)、样本a（蓝色直方图）、抽样的均值分布（红色直方图）三者画在一起。

df.samples.of.30 %>%
  ggplot(aes(x = sample.mean, y = stat(density))) +
  geom_histogram(bins = 50, fill = "firebrick", alpha = 0.5) +
  geom_histogram(
    data = sample.a,
    aes(x = height, y = stat(density)),
    bins = 11, fill = "steelblue", alpha = 0.25
  ) +
  geom_vline(xintercept = true.mean, linetype = "dashed", color = "red") +
  geom_line(data = pop.distn, aes(x = height, y = density), alpha = 0.25, size = 1.5) +
  xlim(125, 225)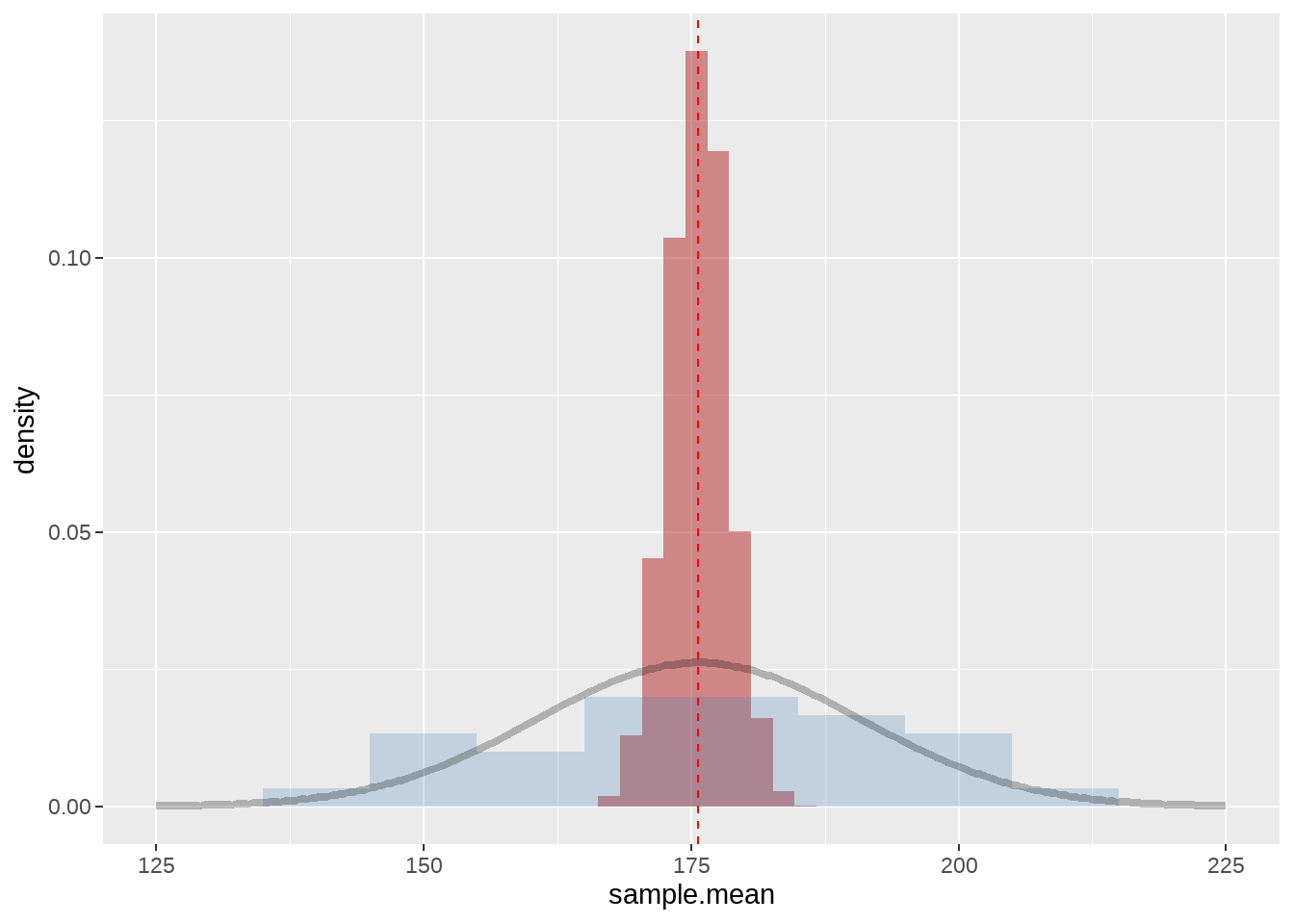

样本的均值分布，是个很有意思的结果，比如，我们再选30个男生再抽样一次，我们可以断定，这次抽样的均值会落在了红色的区间之内。

然而，注意到，必须限定再次抽样的大小仍然是30个男生，以上这句话才成立。

df.samples.of.30 %>%
  summarize(
    mean.of.means = mean(sample.mean),
    sd.of.means = sd(sample.mean)
  )

## # A tibble: 1 × 2
##   mean.of.means sd.of.means
##           <dbl>       <dbl>
## 1          176.        2.77

这里计算的是抽样(样本大小为30)均值分布，而不是整体的均值分布。言外之意，样本大小可以是其它的呗， 那就把样本调整为50、100、250、500分别试试看

df.samples.of.50 <-
  rerun(2500, rnorm.stats(50, true.mean, true.sd)) %>%
  bind_rows()

df.samples.of.100 <-
  rerun(2500, rnorm.stats(100, true.mean, true.sd)) %>%
  bind_rows()

df.samples.of.250 <-
  rerun(2500, rnorm.stats(250, true.mean, true.sd)) %>%
  bind_rows()

df.samples.of.500 <-
  rerun(2500, rnorm.stats(500, true.mean, true.sd)) %>%
  bind_rows()

忍不住想画图看看，每次抽取的男生数量不同，均值的分布会有不同？

df.combined <-
  bind_rows(
    df.samples.of.30,
    df.samples.of.50,
    df.samples.of.100,
    df.samples.of.250,
    df.samples.of.500
  ) %>%
  mutate(sample.sz = as.factor(sample.size))

df.combined %>%
  ggplot(aes(x = sample.mean, y = stat(density), fill = sample.sz)) +
  geom_histogram(bins = 25, alpha = 0.5) +
  geom_vline(xintercept = true.mean, linetype = "dashed") +
  facet_wrap(vars(sample.sz), nrow = 1) +
  scale_fill_brewer(palette = "Set1") +
  labs(
    x = "Sample means", y = "Density",
    title = "Distribution of mean heights for samples of varying size"
  )

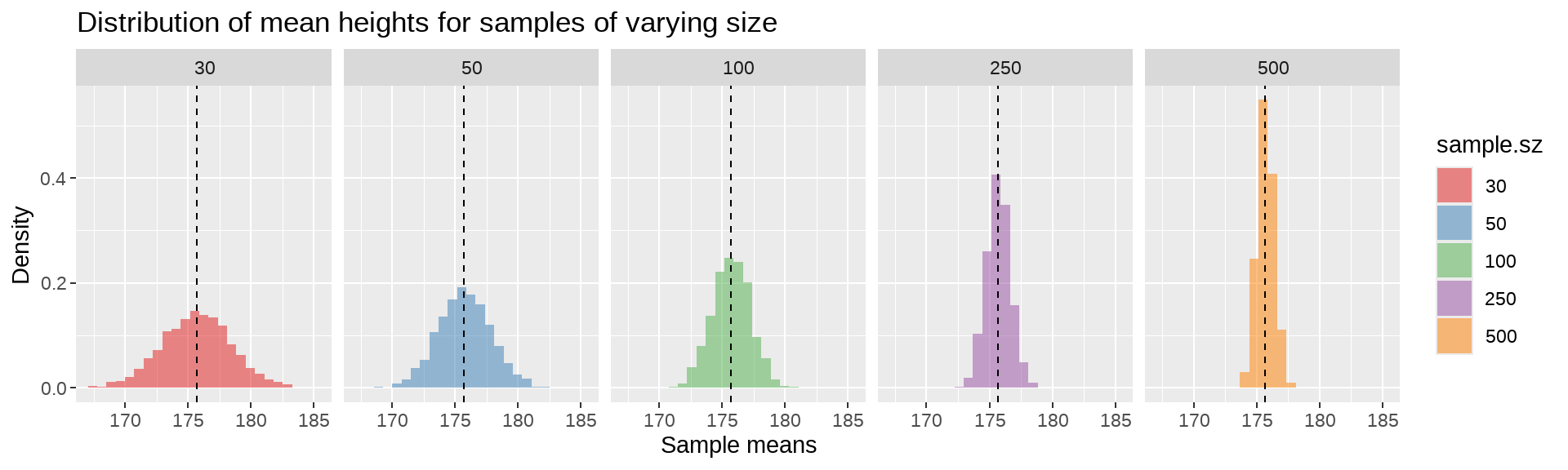
随着样本大小由30增加到500，抽样的均值分布围绕着越来越聚合到实际的均值，或者说随着样本大小的增多，对均值估计的不确定性越小。

sampling.distn.mean.table <-
  df.combined %>%
  group_by(sample.size) %>%
  summarize(
    mean.of.means = mean(sample.mean),
    sd.of.means = sd(sample.mean)
  )
sampling.distn.mean.table

## # A tibble: 5 × 3
##   sample.size mean.of.means sd.of.means
##         <dbl>         <dbl>       <dbl>
## 1          30          176.       2.77 
## 2          50          176.       2.11 
## 3         100          176.       1.51 
## 4         250          176.       0.948
## 5         500          176.       0.672

有个统计学上的概念需要明确。

输出结果的第三列sd.of.means 是不同样本大小(30,50,100,250,500)下，反复抽样后平均数分布的标准差。

数学上，如果已知总体的标准差(\(\sigma\))，那么抽取无限多份大小为 \(n\) 的样本，每个样本各有一个平均值，所有这个大小的样本之平均值的标准差可证明为

\[ \frac{\sigma}{\sqrt{n}} \] 即，平均值的标准误差。

下面我们画图看看，模拟出来的\(sd.of.means\)和理论值\(\frac{\sigma}{\sqrt{n}}\)是否一致。

注意到这里的\(\sigma\)是总体的标准差，即最开始我们设定的川师男生身高的标准差true.sd. 也就说，理论上

df.se.mean.theory <- tibble(
  sample.size = seq(10, 500, 10)
) %>%
  mutate(std.error = true.sd / sqrt(sample.size))

df.se.mean.theory

## # A tibble: 50 × 2
##    sample.size std.error
##          <dbl>     <dbl>
##  1          10      4.80
##  2          20      3.40
##  3          30      2.77
##  4          40      2.40
##  5          50      2.15
##  6          60      1.96
##  7          70      1.82
##  8          80      1.70
##  9          90      1.60
## 10         100      1.52
## # ℹ 40 more rows

平均值标准误差随样本大小变化

sampling.distn.mean.table %>%
  ggplot(aes(x = sample.size, y = sd.of.means)) +
  geom_point() +
  geom_line(aes(x = sample.size, y = std.error),
    data = df.se.mean.theory,
    color = "red"
  ) +
  labs(
    x = "Sample size", y = "Std Error of Mean",
    title = "Standard error of mean value varies with sample size (comparison between theoretical value and simulated value)"
  )

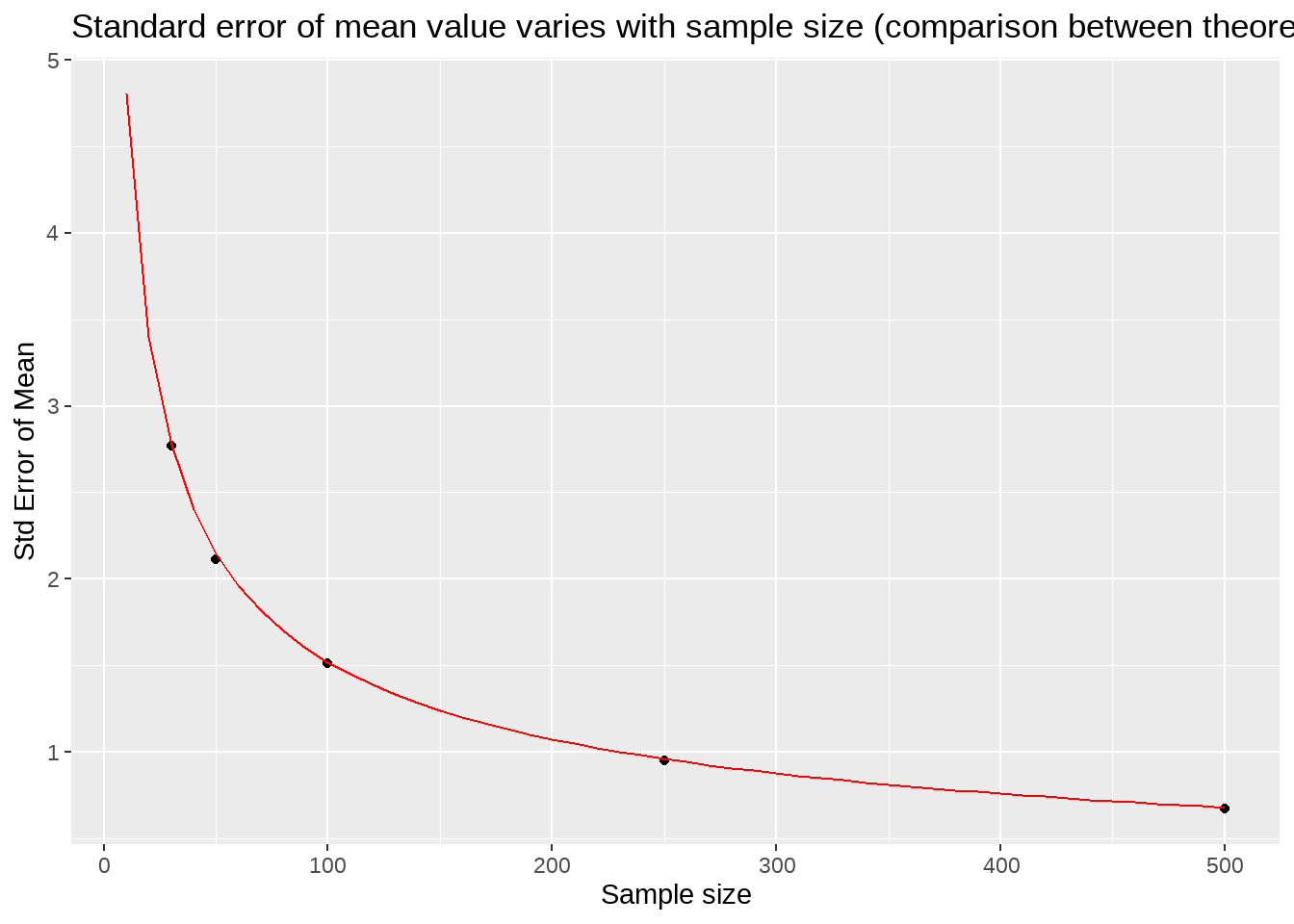
两者吻合的很好。

刚刚我们看到的，抽样均值分布随着样本大小变化而变化。可以试想下，抽样的其他统计量分布（方差，中位数），是不是也随着样本大小变化而变化呢？

sampling.distn.sd.table <-
  df.combined %>%
  group_by(sample.size) %>%
  summarize(
    mean.of.sds = mean(sample.sd),
    sd.of.sds = sd(sample.sd)
  )

sampling.distn.sd.table

## # A tibble: 5 × 3
##   sample.size mean.of.sds sd.of.sds
##         <dbl>       <dbl>     <dbl>
## 1          30        15.1     1.99 
## 2          50        15.1     1.56 
## 3         100        15.2     1.07 
## 4         250        15.2     0.681
## 5         500        15.2     0.486

答案是肯定的，样本量的增多，抽样方差的不确定性减少。

48.5 扩展阅读

• https://learningstatisticswithr.com/book/