第 71 章贝叶斯混合模型

library(tidyverse)
library(tidybayes)
library(rstan)
rstan_options(auto_write = TRUE)
options(mc.cores = parallel::detectCores())

71.1 僧侣抄经书

寺庙里，僧侣每天会完成少部分的经书，每个僧侣独立工作，由于经书长度不同，因此，有时候会有3本以上的经书完成，有时候一本都没有，这个过程本质上可以看作是二项过程，

rbinom(n = 100, size = 5, prob = 0.2)

##   [1] 0 1 1 0 1 1 1 2 1 1 2 1 0 1 0 3 0 2 2 0 2 0 1 0 2 2 1 1 1 0 0 2 1 1 2 1 1
##  [38] 1 1 0 0 2 1 1 2 0 0 2 2 0 0 1 0 1 1 2 2 1 1 0 3 0 2 1 0 0 0 1 0 2 2 0 2 1
##  [75] 0 1 2 1 0 1 1 2 0 2 1 0 0 1 2 2 1 0 1 1 1 1 0 0 2 0

n = 100，表示试验100次，生成的向量会有100个元素
size = 5，这里有5个硬币(有正反面)
prob = 0.2，每个硬币朝正面的概率是0.2

结果：统计这5个硬币中朝正面的共有多少个，这个只是n=1的结果。现在这5个硬币的实验，重复100次，对应着100个结果。代码就是生成了100个元素的向量。

当实验次数n很大，同时每次成功的几率prob又很小，该过程接近泊松。用泊松似然函数建模，模型的形式比二项模型更加简单，因为它只有一个均值参数。

\[ \text{Poisson}(n|\lambda) = \frac{1}{n!} \, \lambda^n \, \exp(-\lambda). \]

71.2 僧侣要喝酒

现在，假设僧侣某些天要休息，在休息天里，他们会去喝酒，因此没有任何经书产出。

71.3 混合模型

通常情况下，我们测量到的不是某一个单一过程的结果，而是不同过程的混合结果。当观测值背后的原因有多种的时候，可以使用混合模型。混合模型用多个简单的概率分布对多种原因的结果变量进行建模。数学上，可以看作，模型对结果变量使用多个似然函数。

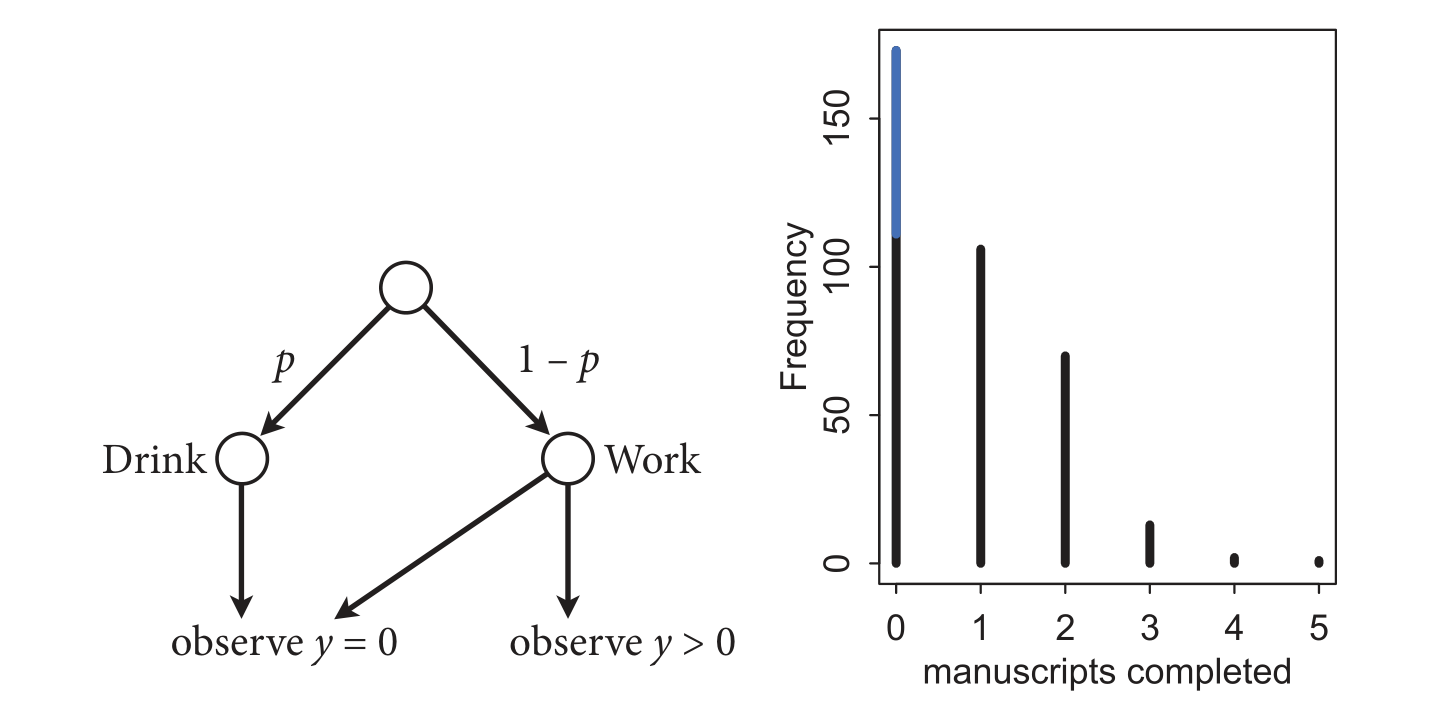
让我们用混合模型来思考僧侣抄经书问题，考虑如下：数据中任何经书产出为0观测的原因有两个：

每天喝酒没抄经书
工作但没有完成任何经书

假设 \(p\) 是僧侣喝酒的概率，\(\lambda\) 是僧侣工作时平均完成经书的数目。那么，是否喝酒可以通过投掷硬币来决定，根据硬币的正反面来决定是喝酒或者抄经书。喝酒的僧侣不能抄经书，而抄经书的僧侣完成的经书数目是一个均值为 \(\lambda\) 的泊松分布，以上写成数学形式：

观测到 \(y = 0\) 的概率 \[ \begin{align*} \text{Pr}(0 | p, \lambda) & = \text{Pr}(\text{drink} | p) + \text{Pr}(\text{work} | p) \times \text{Pr}(0 | \lambda) \\ & = p + (1 - p) \; \exp (- \lambda). \end{align*} \]
观测到 \(y > 0\) 对应的似然函数

\[ \begin{align*} \text{Pr}(y | p, \lambda) & = \text{Pr}(\text{drink} | p) (0) + \text{Pr}(\text{work} | p) \text{Pr}(y | \lambda) \\ & = (1 - p) \frac {\lambda^y \; \exp (- \lambda)}{y!} \end{align*} \]

71.3.1 zero-inflated Poisson模型的数学表达式

将上面的过程，定义为零膨胀泊松分布回归模型(zero-inflated Poisson)，其中，参数分布 \(p\) (结果为0的概率)和描述分布形状的参数 \(\lambda\) (泊松分布的均值)，

\[ \begin{align*} y_i & \sim \operatorname{ZIPoisson}(p_i, \lambda_i)\\ \operatorname{logit}(p_i) & = \alpha_p + \beta_p x_i \\ \log (\lambda_i) & = \alpha_\lambda + \beta_\lambda x_i. \end{align*} \]

本次模型中，不需要任何预测变量 \(x\)

这里有两个线性模型和两个链接函数，分别对应ZIPoisson中的两个过程，线性模型的参数不相同。

现在需要的部分都齐全了，就差数据。接下来模拟僧侣数据，然后建立模型得到相应的参数估计，你会发现得到的结果能还原模拟数据的设置

# define parameters
prob_drink <- 0.2  # 20% of days
rate_work  <- 1    # average 1 manuscript per day

# sample one year of production
n <- 365
# simulate days monks drink
set.seed(11)
drink <- rbinom(n, 1, prob_drink)
# simulate manuscripts completed
y <- (1 - drink) * rpois(n, rate_work)

以上代码模拟了一年365天中，每一天完成经书的数量。（等价于，正常的rpois分布生成的向量，这一向量，乘以随机硬币，变成喝酒的天，从而对应的向量元素变为0）。

可以先画个图

library(ggthemes)

d <-
  tibble(Y = y) %>%
  arrange(Y) %>% 
  mutate(zeros = c(rep("zeros_drink", times = sum(drink)),
                   rep("zeros_work",  times = sum(y == 0 & drink == 0)),
                   rep("nope",        times = n - sum(y == 0)))
         ) 

d %>% 
  ggplot(aes(x = Y)) +
  geom_histogram(aes(fill = zeros),
                 binwidth = 1, size = 1/10, color = "grey92") +
  scale_fill_manual(values = c(canva_pal("Green fields")(4)[1], 
                               canva_pal("Green fields")(4)[2], 
                               canva_pal("Green fields")(4)[1])) +
  xlab("Manuscripts completed") +
  theme_hc() +
  theme(legend.position = "none")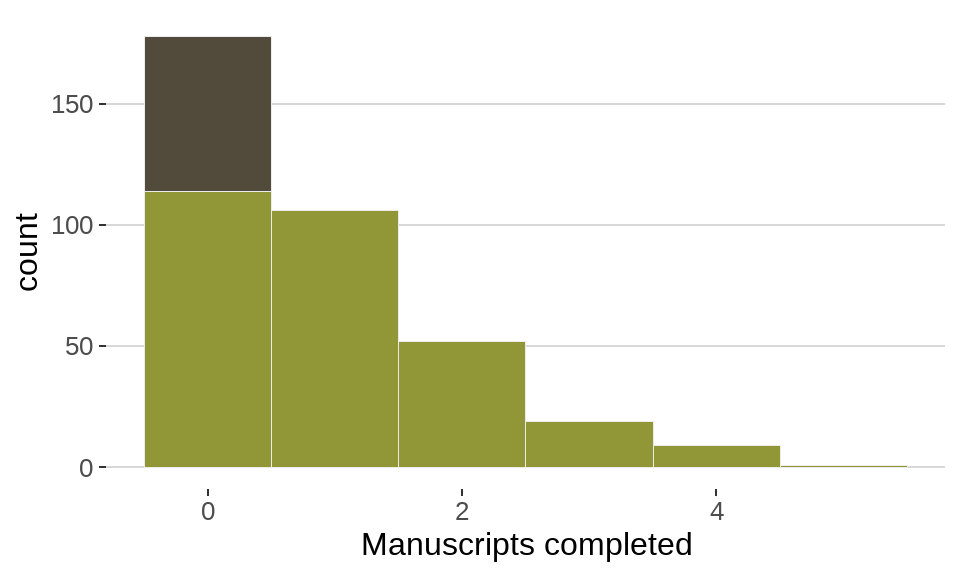

图中用黑色表示由于喝酒导致的零观测，用墨绿色代表工作时产生的观测。和标准的泊松分布相比，存在零膨胀的现象。

71.3.2 Stan 代码

stan_program <- "
data {
    int n;
    int y[n];
}
parameters {
    real ap;
    real al;
}
model {
    real p;
    real lambda;
    p = inv_logit(ap);
    lambda = exp(al);
    
    ap ~ normal(-1.5, 1);
    al ~ normal(1, .5);
    
    for ( i in 1:n ) {
        if (y[i] == 0)
            target += log_mix( p , 0 , poisson_lpmf(0 | lambda) );
        if (y[i] > 0)
            target += log1m( p ) + poisson_lpmf(y[i] | lambda );
    }
}
"


stan_data <- list(
  n = length(y),
  y = y
) 
  

fit <- stan(model_code = stan_program, data = stan_data)

summary(fit, c('al', 'ap'))$summary

##           mean     se_mean         sd        2.5%         25%        50%
## al  0.09788969 0.002230667 0.08366158 -0.07059784  0.04401349  0.1009258
## ap -1.26929212 0.008606286 0.32480816 -2.02371056 -1.45499581 -1.2292388
##           75%      97.5%    n_eff     Rhat
## al  0.1557251  0.2545978 1406.639 1.002628
## ap -1.0464590 -0.7282135 1424.368 1.001551

在原尺度下，

exp(0.09780912)

## [1] 1.102752

inv_logit <- function(x) {
  exp(x) / (1 + exp(x))
}


inv_logit(-1.25875323)

## [1] 0.2211886

我们得到僧侣喝酒天数的比例 0.22，和模拟时用的设置0.2比较，说明参数还原的不错。

fit %>%
  tidybayes::gather_draws(ap) %>%
  tidybayes::mean_qi(.width = .89) %>% 
  ungroup()

## # A tibble: 1 × 7
##   .variable .value .lower .upper .width .point .interval
##   <chr>      <dbl>  <dbl>  <dbl>  <dbl> <chr>  <chr>    
## 1 ap         -1.27  -1.83 -0.822   0.89 mean   qi

70 贝叶斯层级模型

72 贝叶斯分类模型