Skip to main content

数据科学中的 R 语言

第 50 章 模拟与抽样3

我很推崇infer基于模拟的假设检验。本节课的内容是用tidyverse技术重复infer过程，让统计分析透明。

library(tidyverse)
library(infer)

penguins <- palmerpenguins::penguins %>% drop_na()

point_estimate <- penguins %>%
  specify(response = bill_length_mm) %>%
  calculate(stat = "mean")

penguins %>%
  specify(response = bill_length_mm) %>%
  hypothesize(null = "point", mu = 40) %>%
  generate(reps = 5000, type = "bootstrap") %>%
  calculate(stat = "mean") %>%
  visualize() +
  shade_p_value(obs_stat = point_estimate, direction = "two-sided")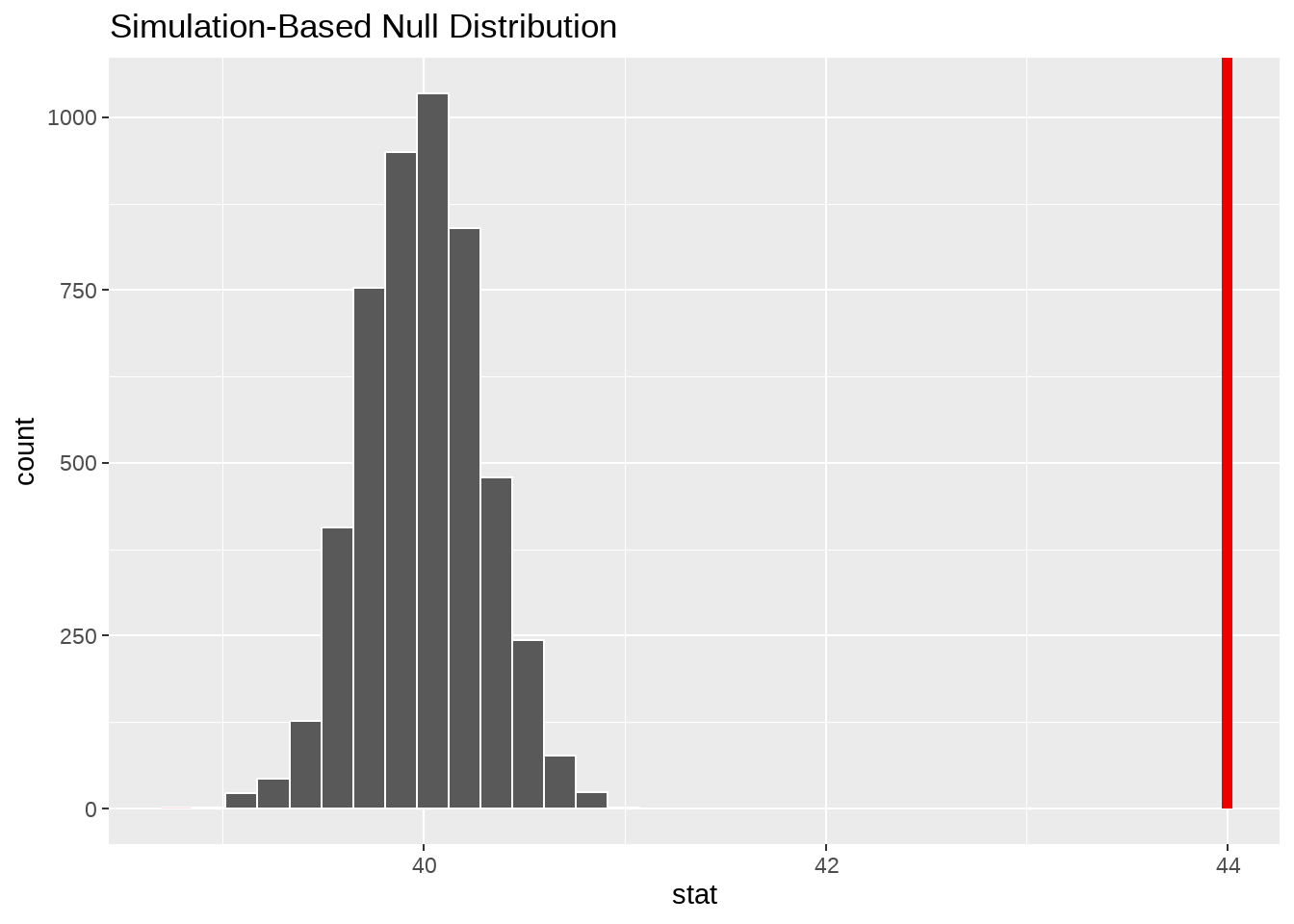

50.1 重复infer中null = "point"的抽样过程

  • 零假设，bill_length_mm长度的均值是mu = 40.

具体怎么做呢？

50.1.1 抽样

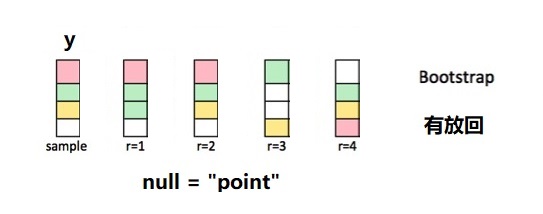
  • 响应变量y这一列，先中心化，然后加上假设条件mu
  • 针对调整后的这一列，有放回的抽样。
  • 反复抽样reps = 1000次

由图中可以看到，每次抽样返回的新数据框与原数据框大小相等，但因为是有放回的抽样，因此每次得到一个不同的集合，有的值可能没抽到，而有的值抽了好几次。下面以一个小的数据框为例演示

tbl <- tibble(
  y = 1:4,
  x = c("a", "a", "b", "b")
)
tbl
## # A tibble: 4 × 2
##       y x    
##   <int> <chr>
## 1     1 a    
## 2     2 a    
## 3     3 b    
## 4     4 b
tbl %>%
  specify(response = y) %>%
  hypothesize(null = "point", mu = 4) %>%
  generate(reps = 1, type = "bootstrap")

先调整y列，然后有放回的抽样

mu <- 4
y <- tbl[[1]] - mean(tbl[[1]]) + mu
y_prime <- sample(y, size = length(y), replace = TRUE)
  
tbl[1] <- y_prime 
tbl

也可以写成函数形式

bootstrap_once <- function(df, mu) {
  y <- df[[1]] - mean(df[[1]]) + mu
  y_prime <- sample(y, size = length(y), replace = TRUE)
  
  df[[1]] <- y_prime
  return(df)
}

tbl %>% bootstrap_once(mu = 4)
## # A tibble: 4 × 2
##       y x    
##   <dbl> <chr>
## 1   5.5 a    
## 2   3.5 a    
## 3   4.5 b    
## 4   5.5 b

这个操作需要重复若干次，比如100次，即得到100个数据框，因此可以使用purrr::map()迭代

1:100 %>% 
   purrr::map(~ bootstrap_once(tbl))

为方便灵活定义重复的次数，也可以改成函数，并且为每次返回的样本(数据框)，编一个序号

bootstrap_repeat <- function(df, reps = 30, mu = mu){
  df_out <- 
    purrr::map_dfr(.x = 1:reps, .f = ~ bootstrap_once(df, mu = mu)) %>% 
    dplyr::mutate(replicate = rep(1:reps, each = nrow(df))) %>% 
    dplyr::group_by(replicate)
  
  return(df_out)
}

tbl %>% bootstrap_repeat(reps = 1000, mu = 4)
## # A tibble: 4,000 × 3
## # Groups:   replicate [1,000]
##        y x     replicate
##    <dbl> <chr>     <int>
##  1   4.5 a             1
##  2   4.5 a             1
##  3   2.5 b             1
##  4   2.5 b             1
##  5   2.5 a             2
##  6   4.5 a             2
##  7   3.5 b             2
##  8   2.5 b             2
##  9   4.5 a             3
## 10   3.5 a             3
## # ℹ 3,990 more rows

50.1.2 计算null假设分布

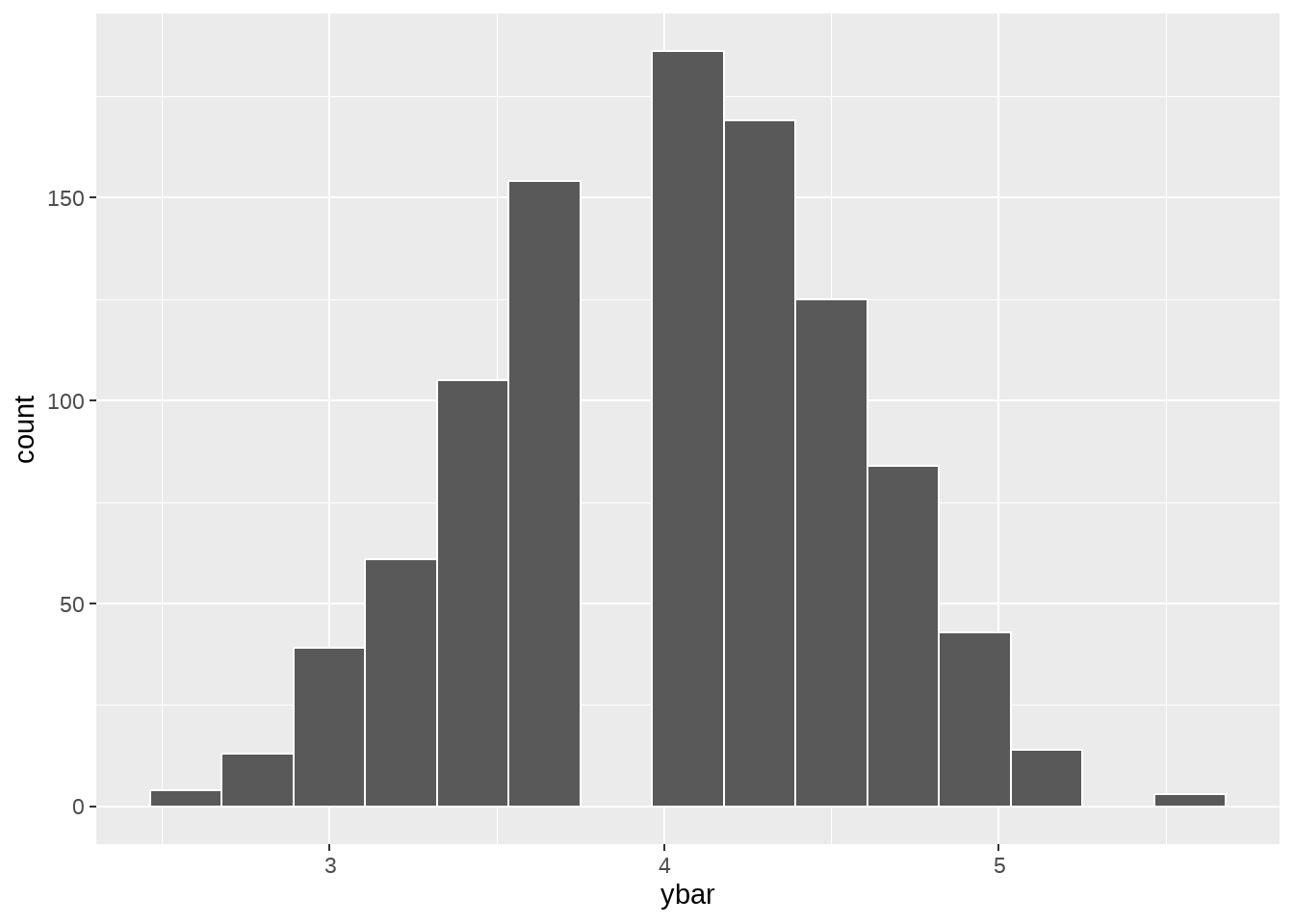
计算每次抽样中，y的均值

null_dist <- tbl %>% 
  bootstrap_repeat(reps = 1000, mu = 4) %>% 

  group_by(replicate) %>% 
  summarise(ybar = mean(y)) 

null_dist
## # A tibble: 1,000 × 2
##    replicate  ybar
##        <int> <dbl>
##  1         1  5   
##  2         2  3.5 
##  3         3  3.5 
##  4         4  4.75
##  5         5  4.25
##  6         6  5.25
##  7         7  4.5 
##  8         8  3.5 
##  9         9  3.75
## 10        10  4.25
## # ℹ 990 more rows

50.1.3 可视化 

null_dist %>% 
  ggplot(aes(x = ybar)) +
  geom_histogram(bins = 15, color = "white")

50.1.4 应用penguins 

samples <- penguins %>% 
  select(bill_length_mm) %>% 
  bootstrap_repeat(reps = 5000, mu = 40)

null_dist <- samples %>% 
  group_by(replicate) %>% 
  summarise(stat = mean(bill_length_mm)) 

null_dist %>% 
  ggplot(aes(x = stat)) +
  geom_histogram(bins = 15, color = "white")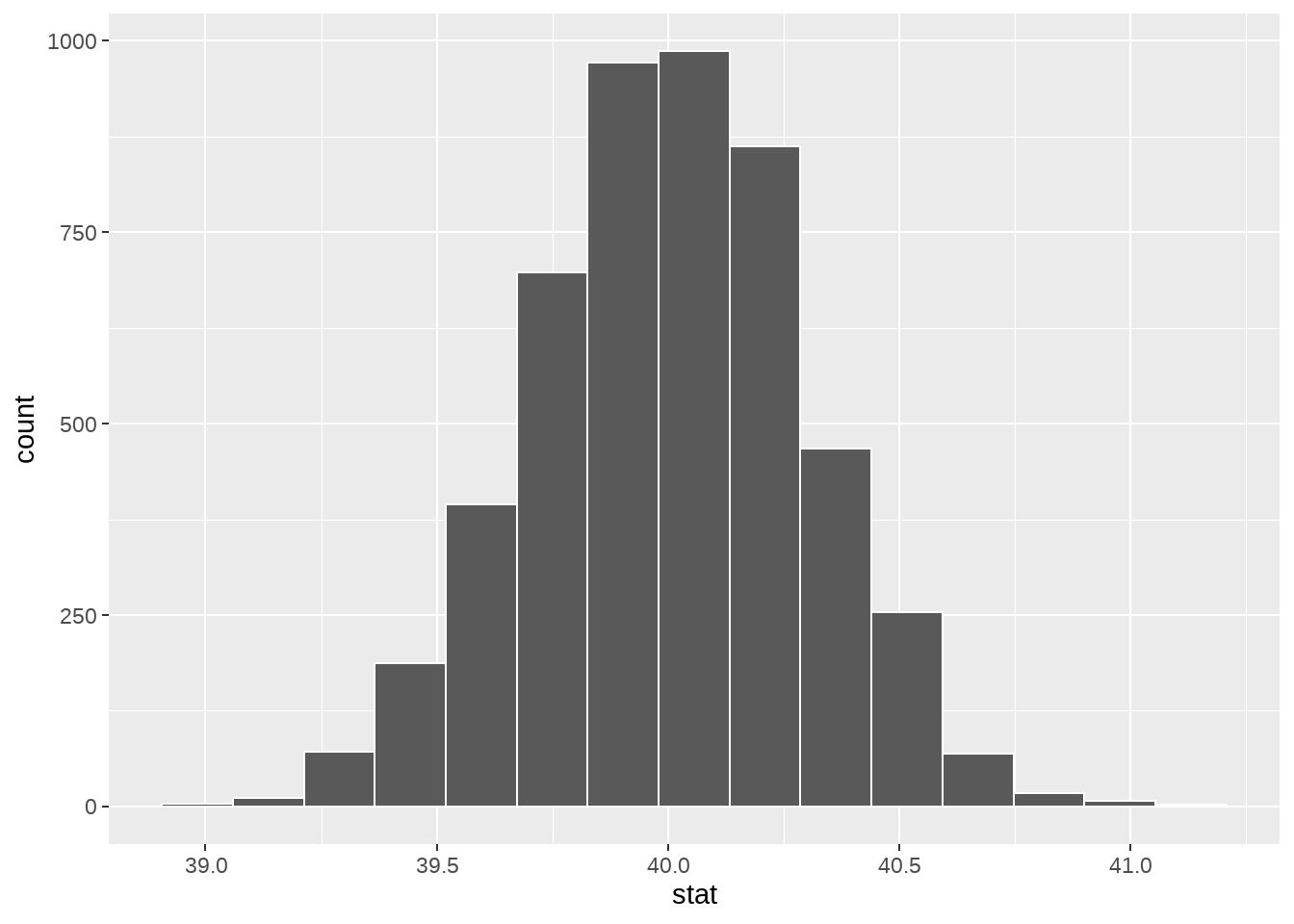
obs_point <- mean(penguins$bill_length_mm)

p_value <- sum(null_dist$stat > obs_point) / length(null_dist$stat)
p_value
## [1] 0

50.1.5 也可以用rowwise()写 

mu <- 40

update <- penguins %>% 
  mutate(
   bill_length_mm = bill_length_mm - mean(bill_length_mm) + mu
  )


null_dist <- tibble(replicate = 1:1000) %>% 
  rowwise() %>% 
  mutate(hand = list(sample(update$bill_length_mm, nrow(update), replace = TRUE))) %>% 
  mutate(points = mean(hand)) %>% 
  ungroup()

null_dist
## # A tibble: 1,000 × 3
##    replicate hand        points
##        <int> <list>       <dbl>
##  1         1 <dbl [333]>   40.0
##  2         2 <dbl [333]>   40.4
##  3         3 <dbl [333]>   40.4
##  4         4 <dbl [333]>   40.2
##  5         5 <dbl [333]>   40.1
##  6         6 <dbl [333]>   40.2
##  7         7 <dbl [333]>   40.1
##  8         8 <dbl [333]>   39.9
##  9         9 <dbl [333]>   39.8
## 10        10 <dbl [333]>   39.9
## # ℹ 990 more rows
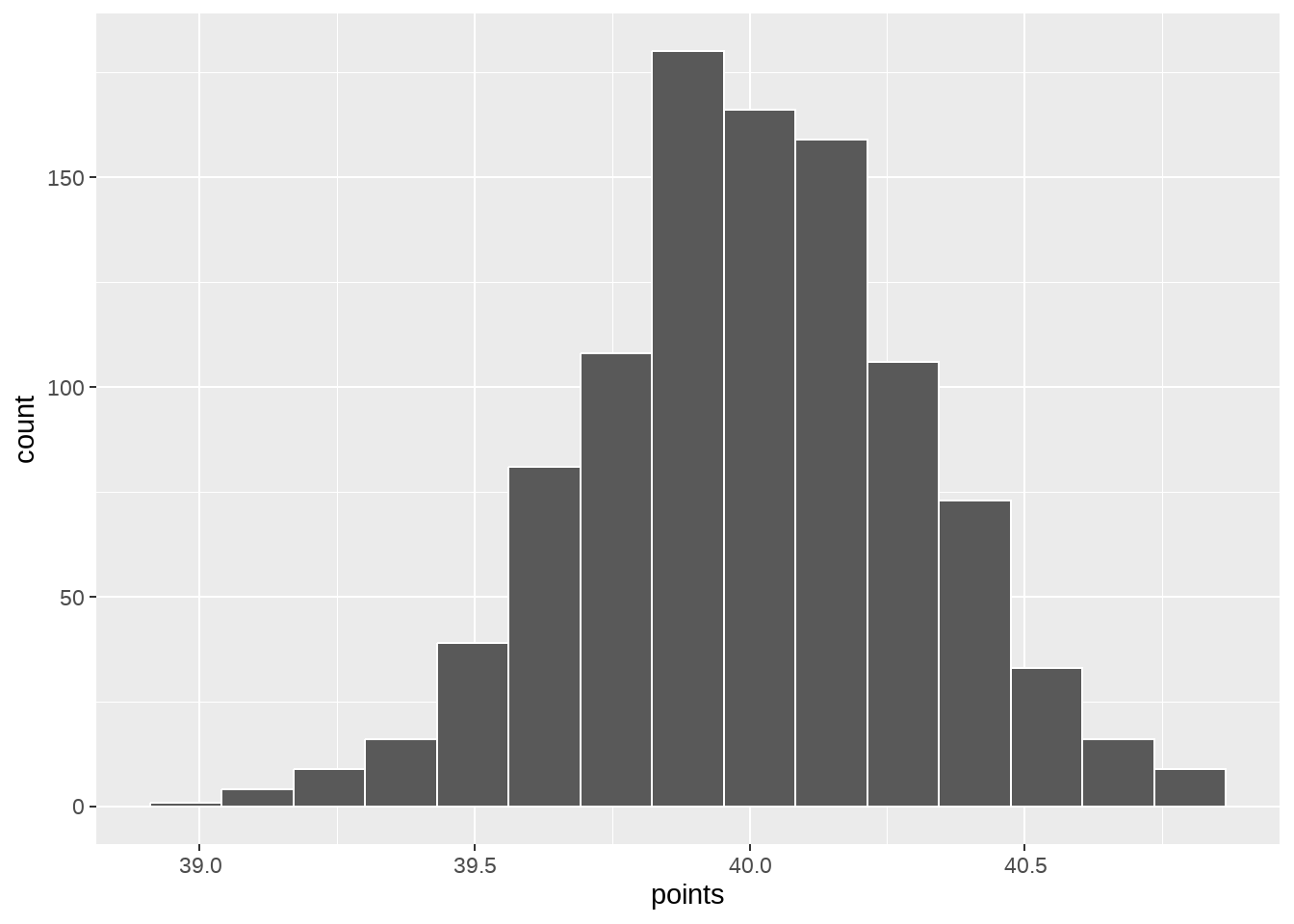
null_dist %>% 
  ggplot(aes(x = points)) +
  geom_histogram(bins = 15, color = "white")