Skip to main content

数据科学中的 R 语言

第 74 章 抽样数据的规整与可视化

在贝叶斯抽样样本量比较大，我们需要规整和可视化，就需要借助一些函数。这里简单介绍tidybayes宏包和它的姊妹宏包 ggdist，更多的技术参数见官方手册。

74.1 企鹅案例

问题简化，我们只挑选Gentoo类企鹅

library(palmerpenguins)

gentoo <- penguins %>% 
  drop_na() %>% 
  filter(species == "Gentoo")

gentoo
## # A tibble: 119 × 8
##    species island bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
##    <fct>   <fct>           <dbl>         <dbl>             <int>       <int>
##  1 Gentoo  Biscoe           46.1          13.2               211        4500
##  2 Gentoo  Biscoe           50            16.3               230        5700
##  3 Gentoo  Biscoe           48.7          14.1               210        4450
##  4 Gentoo  Biscoe           50            15.2               218        5700
##  5 Gentoo  Biscoe           47.6          14.5               215        5400
##  6 Gentoo  Biscoe           46.5          13.5               210        4550
##  7 Gentoo  Biscoe           45.4          14.6               211        4800
##  8 Gentoo  Biscoe           46.7          15.3               219        5200
##  9 Gentoo  Biscoe           43.3          13.4               209        4400
## 10 Gentoo  Biscoe           46.8          15.4               215        5150
## # ℹ 109 more rows
## # ℹ 2 more variables: sex <fct>, year <int>

先看下两个变量的关系

gentoo %>% 
  ggplot(aes(x = bill_length_mm, bill_depth_mm)) +
  geom_point()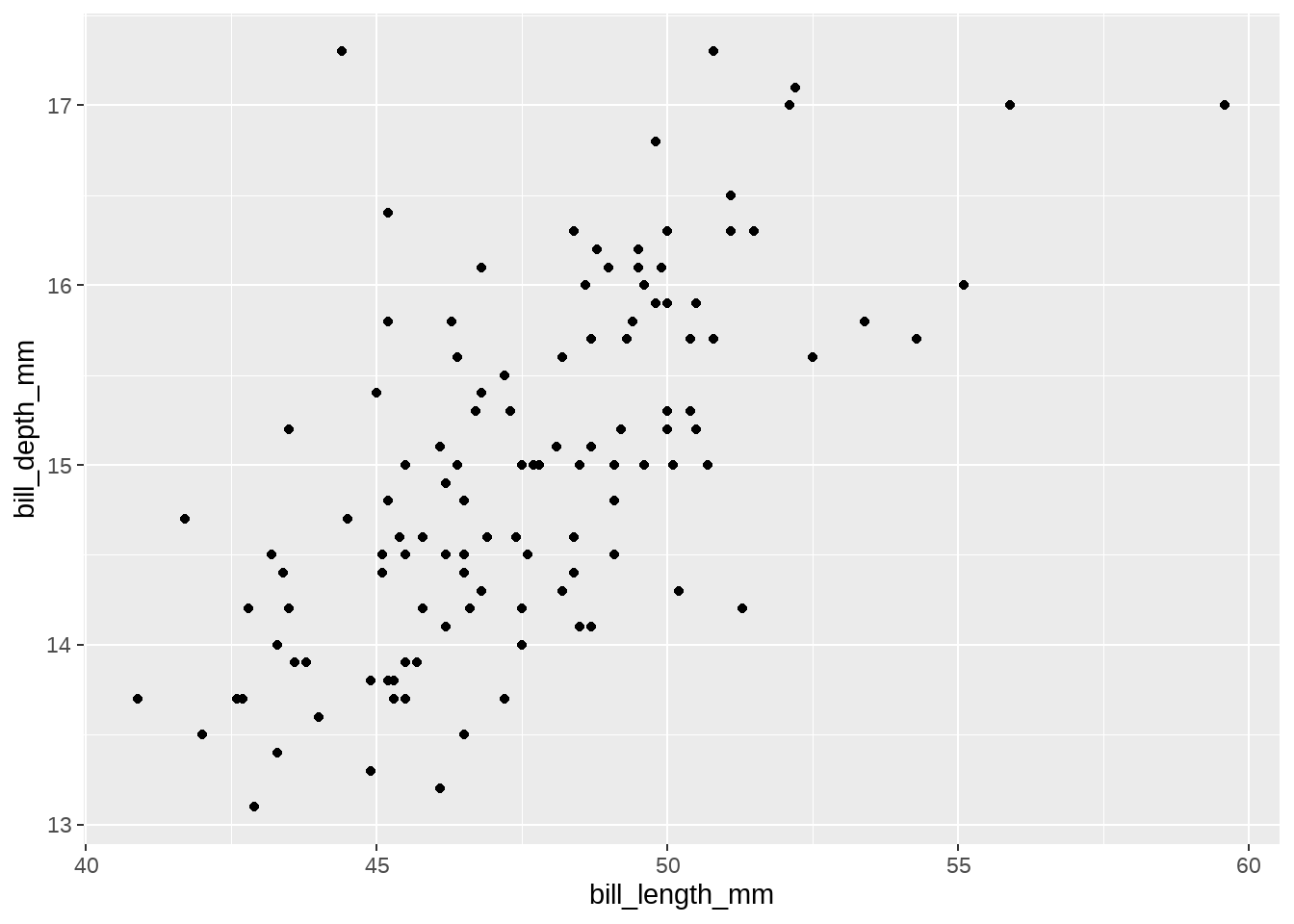

74.2 Stan模型

假设我们建立最简单的线性模型，其中预测因子bill_length_mm，被解释变量是 bill_depth_mm

\[ \begin{align} y_n &\sim \operatorname{normal}(\mu_n, \,\, \sigma)\\ \mu_n &= \alpha + \beta x_n \end{align} \]

stan_program <- "
data {
  int<lower=0> N;
  vector[N] y;
  vector[N] x;
  int<lower=0> M;
  vector[M] new_x;  
}
parameters {
  real alpha;
  real beta;
  real<lower=0> sigma;
}
model {
  y ~ normal(alpha + beta * x, sigma);
  
  alpha  ~ normal(0, 10);
  beta   ~ normal(0, 10);
  sigma  ~ exponential(1);
}
generated quantities {
  vector[M] y_fit;
  vector[M] y_rep;
  for (n in 1:M) {
    y_fit[n] = alpha + beta * new_x[n];
    y_rep[n] = normal_rng(alpha + beta * new_x[n], sigma);
  }
}
"

library(modelr)
newdata <- gentoo %>% 
  data_grid(
    bill_length_mm = seq_range(bill_length_mm, 100)
)

# or
# newdata <- data.frame(
#     bill_length_mm = seq(min(gentoo$bill_length_mm), max(gentoo$bill_length_mm), length.out = 100)
#    ) 


stan_data <- list(
   N = nrow(gentoo),
   x = gentoo$bill_length_mm, 
   y = gentoo$bill_depth_mm,
   M = nrow(newdata),
   new_x = newdata$bill_length_mm
  )

fit <- stan(model_code = stan_program, data = stan_data)

74.3 抽样 

draws <- fit %>% 
  tidybayes::gather_draws(alpha, beta, sigma)
draws
## # A tibble: 12,000 × 5
## # Groups:   .variable [3]
##    .chain .iteration .draw .variable .value
##     <int>      <int> <int> <chr>      <dbl>
##  1      1          1     1 alpha       3.53
##  2      1          2     2 alpha       3.10
##  3      1          3     3 alpha       3.32
##  4      1          4     4 alpha       3.21
##  5      1          5     5 alpha       3.61
##  6      1          6     6 alpha       3.87
##  7      1          7     7 alpha       2.63
##  8      1          8     8 alpha       3.99
##  9      1          9     9 alpha       3.91
## 10      1         10    10 alpha       4.76
## # ℹ 11,990 more rows

74.4 统计汇总 

draws %>% 
  ggdist::mean_qi(.width = c(0.65, 0.89) )
## # A tibble: 6 × 7
##   .variable .value .lower .upper .width .point .interval
##   <chr>      <dbl>  <dbl>  <dbl>  <dbl> <chr>  <chr>    
## 1 alpha      5.06   4.07   6.00    0.65 mean   qi       
## 2 beta       0.209  0.189  0.229   0.65 mean   qi       
## 3 sigma      0.755  0.709  0.801   0.65 mean   qi       
## 4 alpha      5.06   3.33   6.76    0.89 mean   qi       
## 5 beta       0.209  0.173  0.245   0.89 mean   qi       
## 6 sigma      0.755  0.682  0.836   0.89 mean   qi

74.5 可视化

  • geom_slabinterval() / stat_slabinterval() family
draws %>% 
  ggplot(aes(x = .value, y = .variable)) + 
  ggdist::stat_interval()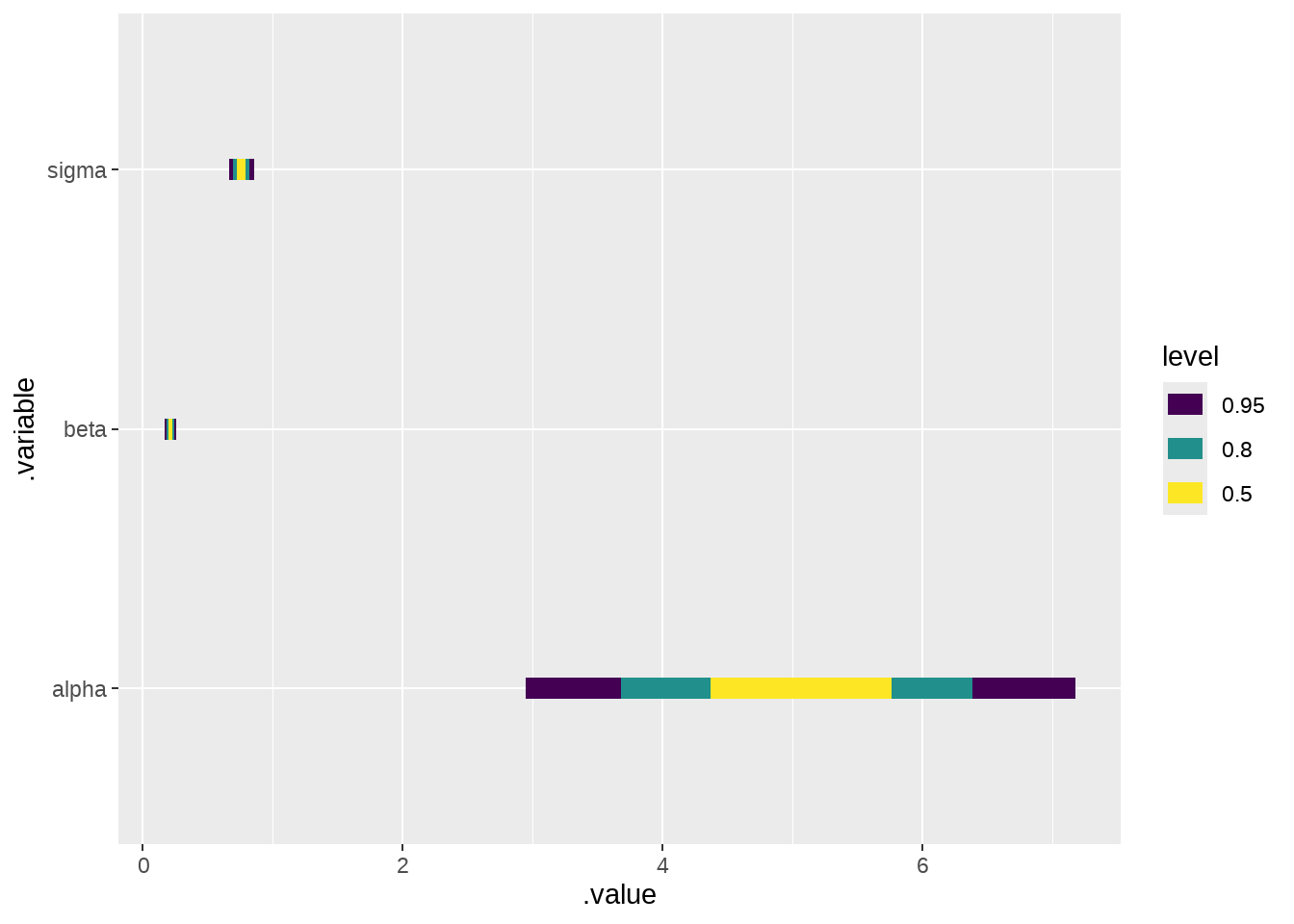
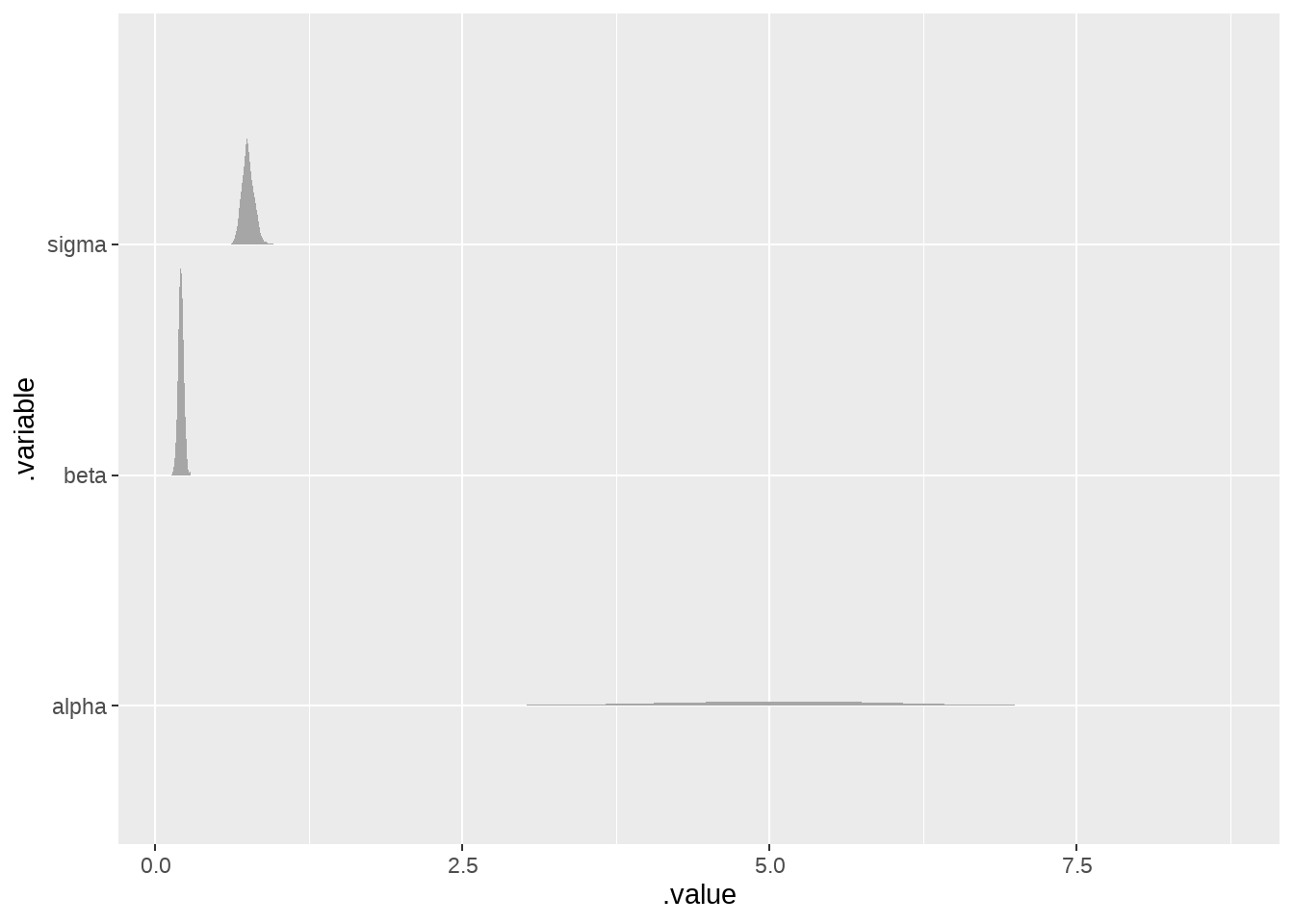
draws %>% 
  ggplot(aes(x = .value, y = .variable)) + 
  ggdist::stat_slab()
draws %>% 
  ggplot(aes(x = .value, y = .variable)) + 
  ggdist::stat_slabinterval()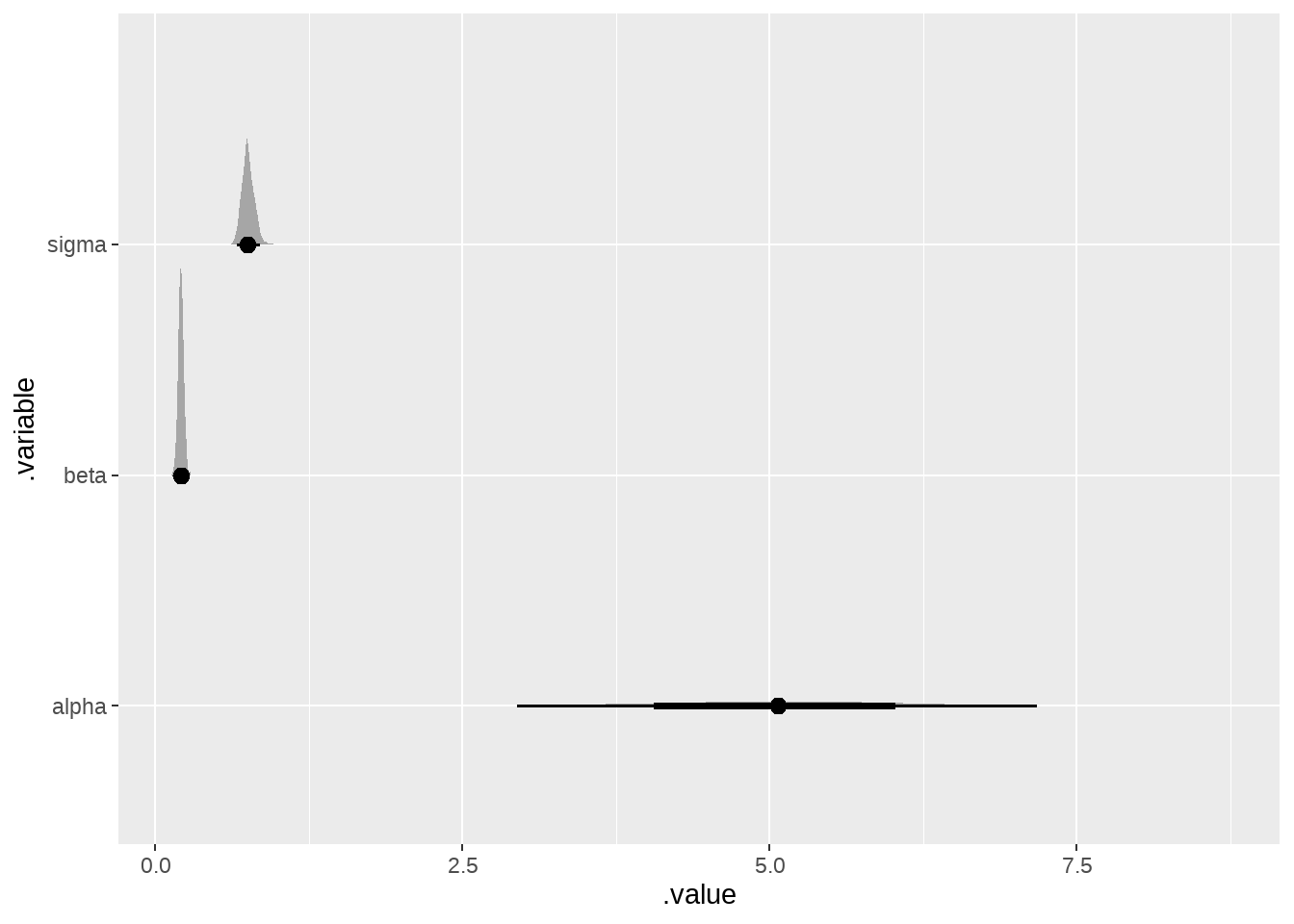
draws %>% 
  filter(.variable %in% c("beta", "sigma")) %>% 
  ggplot(aes(x = .value, y = .variable)) + 
  ggdist::stat_slabinterval()  +
  facet_grid(~ .variable, labeller = "label_both", scales = "free")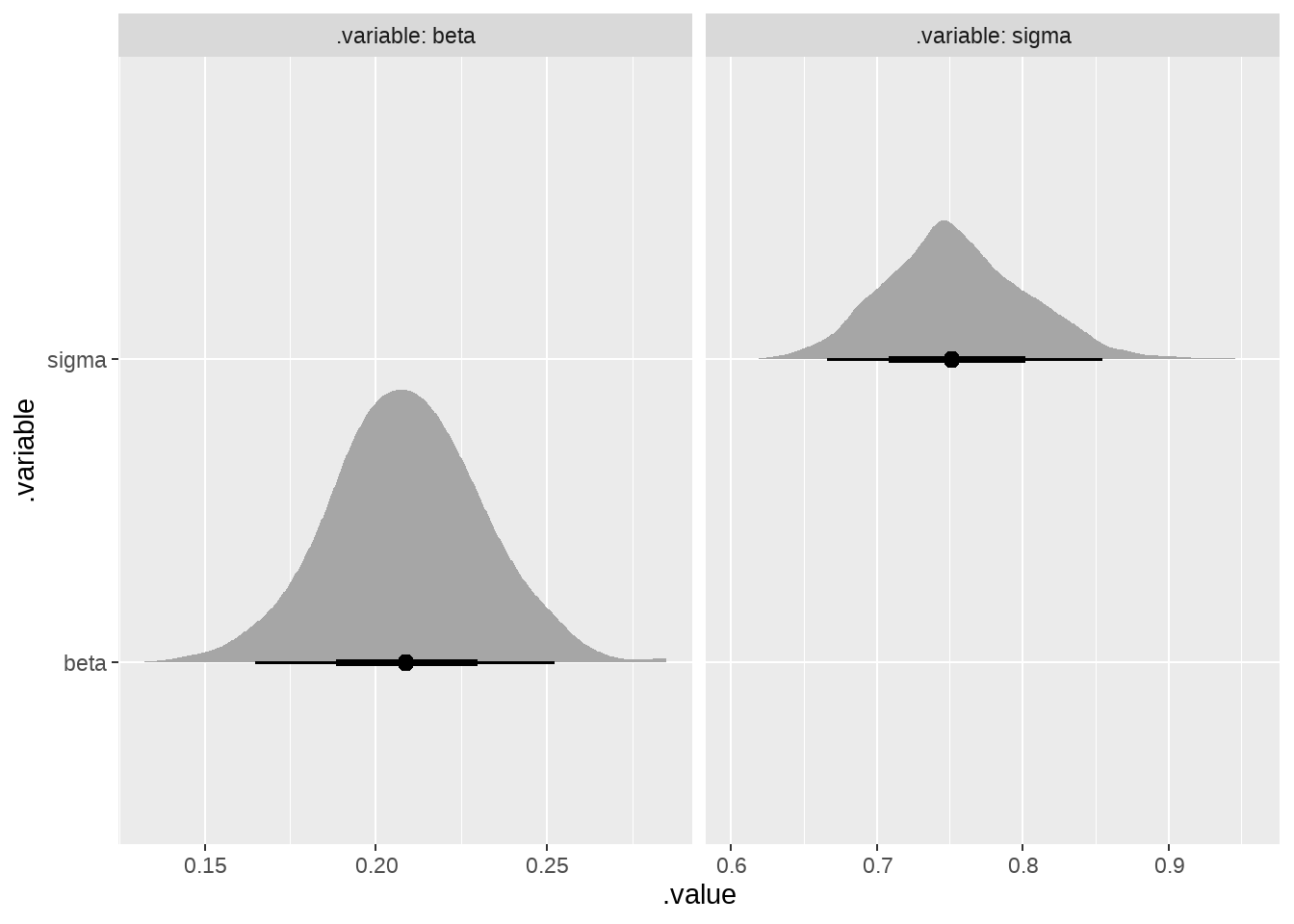
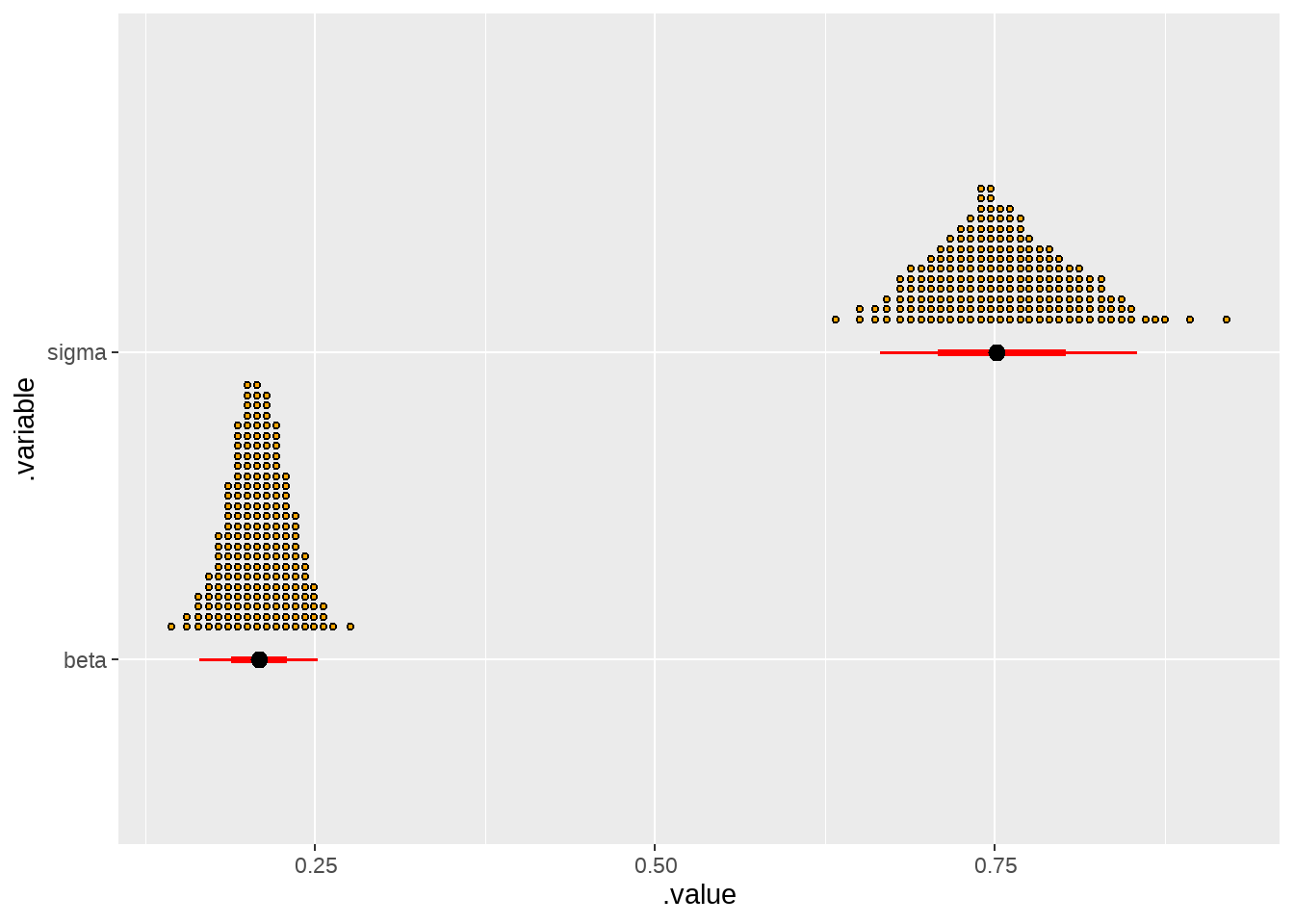
  • geom_dotsinterval() / stat_dotsinterval() family
draws %>% 
  filter(.variable %in% c("beta", "sigma")) %>% 
  ggplot(aes(x = .value, y = .variable)) + 
  stat_dotsinterval(
    quantiles = 200,
    justification = -0.1,
    slab_color = "black",
    slab_fill = "orange",
    interval_color = "red"
  )
  • geom_lineribbon() / stat_lineribbon() family
fit %>% 
  tidybayes::gather_draws(y_fit[i]) %>% 
  ggdist::median_qi(.width = c(0.89)) %>%
  bind_cols(newdata) %>% 
  
  ggplot() + 
  geom_point(
    data = gentoo,
    aes(bill_length_mm, bill_depth_mm)
  ) +
  geom_lineribbon(
    aes(x = bill_length_mm, y = .value, ymin = .lower, ymax = .upper),
    alpha = 0.3, 
    fill = "gray50"
  ) +
  theme_classic() +
  scale_fill_brewer(direction = -1)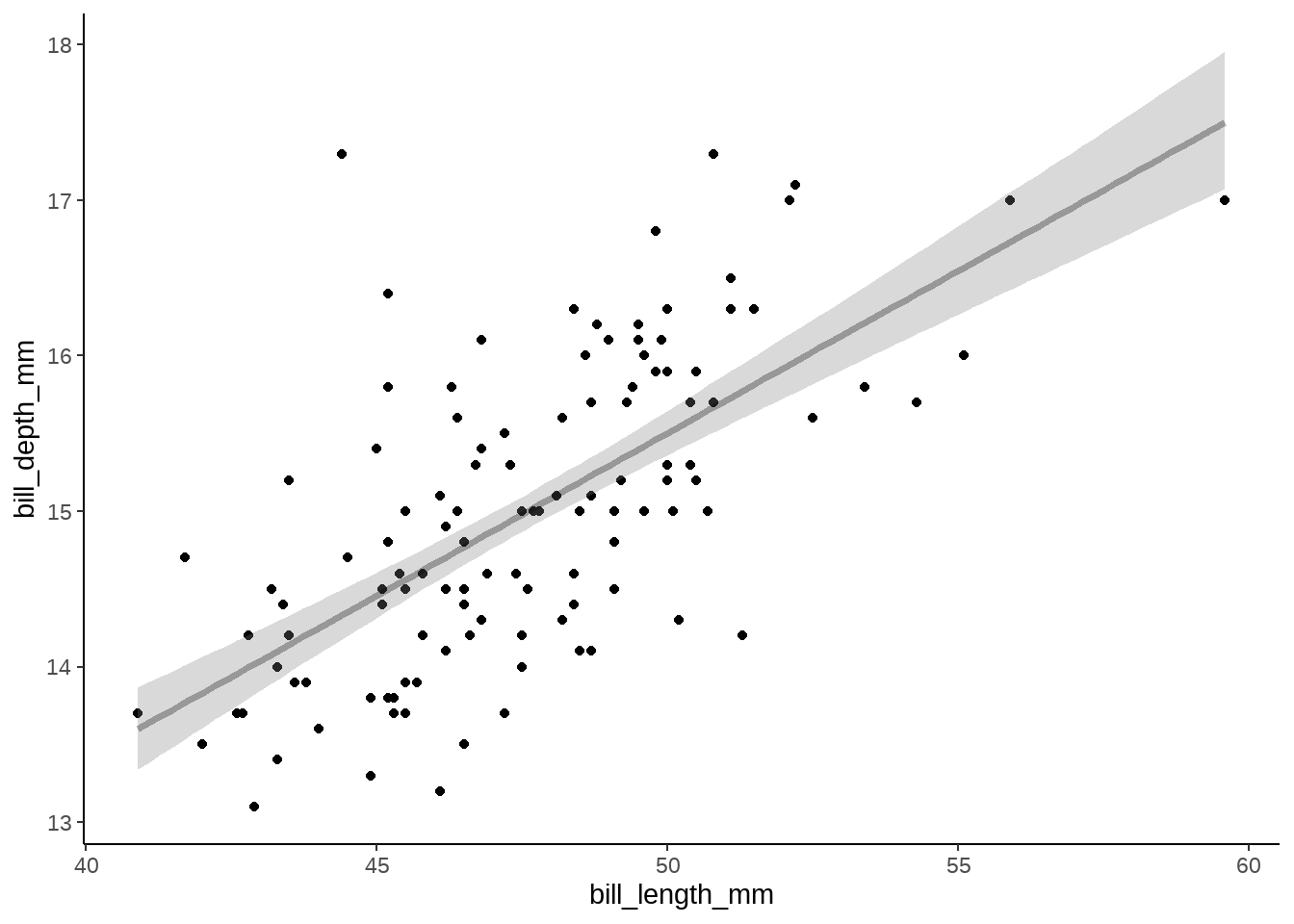
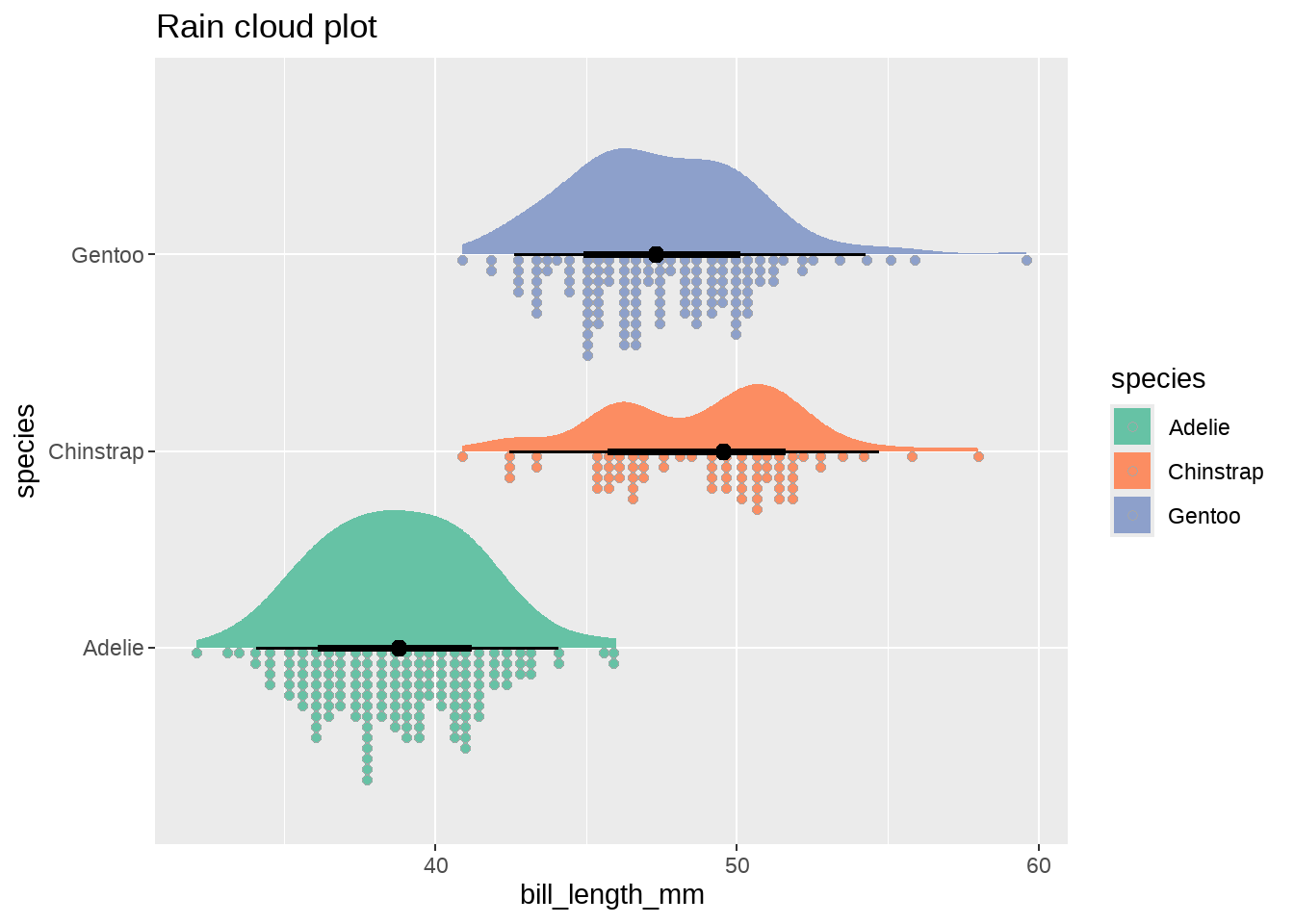
  • 组合
penguins %>%
  ggplot(aes(y = species, x = bill_length_mm, fill = species)) +
  stat_slab(aes(thickness = after_stat(pdf*n)), scale = 0.7) +
  stat_dotsinterval(side = "bottom", scale = 0.7, slab_size = NA) +
  scale_fill_brewer(palette = "Set2") +
  ggtitle("Rain cloud plot")