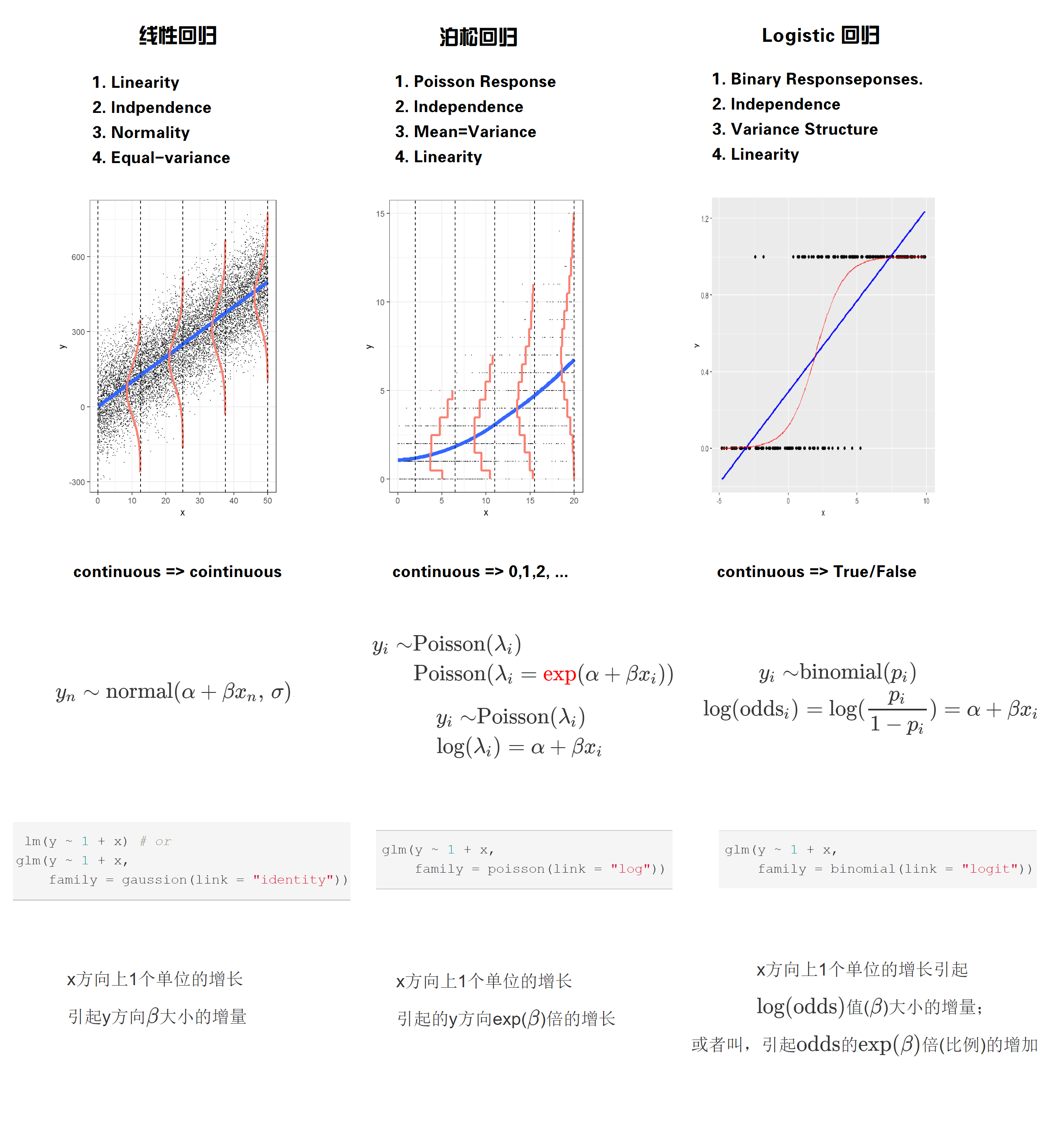
第 58 章 广义线性模型
58.1 线性回归回顾
从线性模型的数学记号 \[ y_n = \alpha + \beta x_n + \epsilon_n \quad \text{where}\quad \epsilon_n \sim \operatorname{normal}(0,\sigma). \]
等价于 \[ y_n - (\alpha + \beta x_n) \sim \operatorname{normal}(0,\sigma), \]
又可以写为 \[ y_n \sim \operatorname{normal}(\alpha + \beta x_n, \, \sigma). \]
线性回归需要满足四个前提假设:
-
Linearity
- 因变量和每个自变量都是线性关系
-
Indpendence
- 对于所有的观测值,它们的误差项相互之间是独立的
-
Normality
- 误差项服从正态分布
-
Equal-variance
- 所有的误差项具有同样方差
这四个假设的首字母,合起来就是LINE,这样很好记
把这四个前提画在一张图中
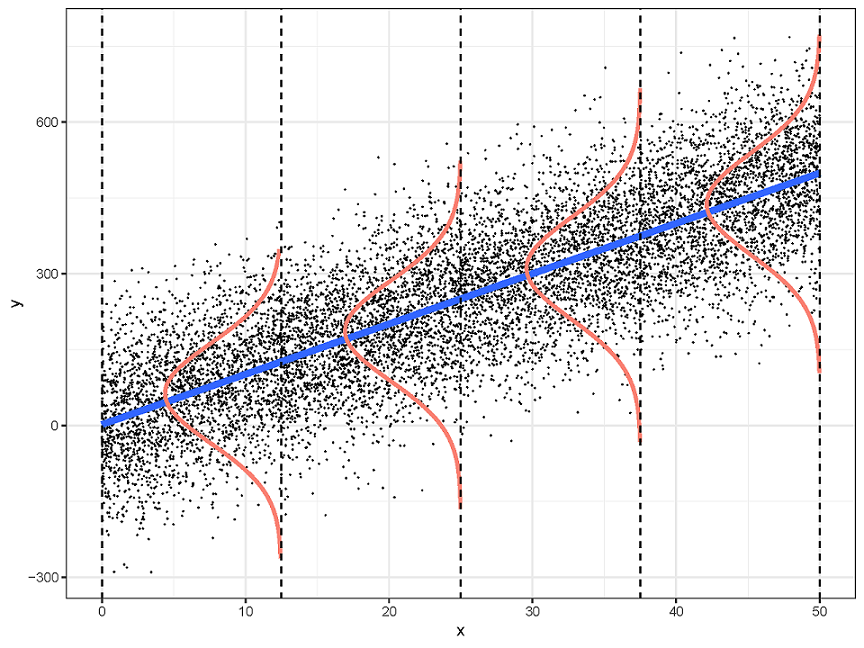
58.2 案例
我们从一个有意思的案例开始。
在受污染的岛屿附近,金枪鱼出现次数

## # A tibble: 200 × 2
## pollution_level number_of_fish
## <dbl> <int>
## 1 0 4
## 2 0.00503 2
## 3 0.0101 1
## 4 0.0151 5
## 5 0.0201 4
## 6 0.0251 1
## 7 0.0302 2
## 8 0.0352 2
## 9 0.0402 3
## 10 0.0452 1
## # ℹ 190 more rows我们的问题是,污染如何影响鱼类的数量?具体来说是想:建立不同位置金枪鱼的数量 与 这个位置的污染程度之间的线性关系。
58.2.1 线性模型的局限性
先看看变量之间的关系
df %>%
ggplot(aes(x = pollution_level, y = number_of_fish)) +
geom_point() +
geom_smooth(method = lm) +
labs(
title = "Number of fish counted under different pollution level",
x = "Pollution level",
y = "Number of fish counted"
)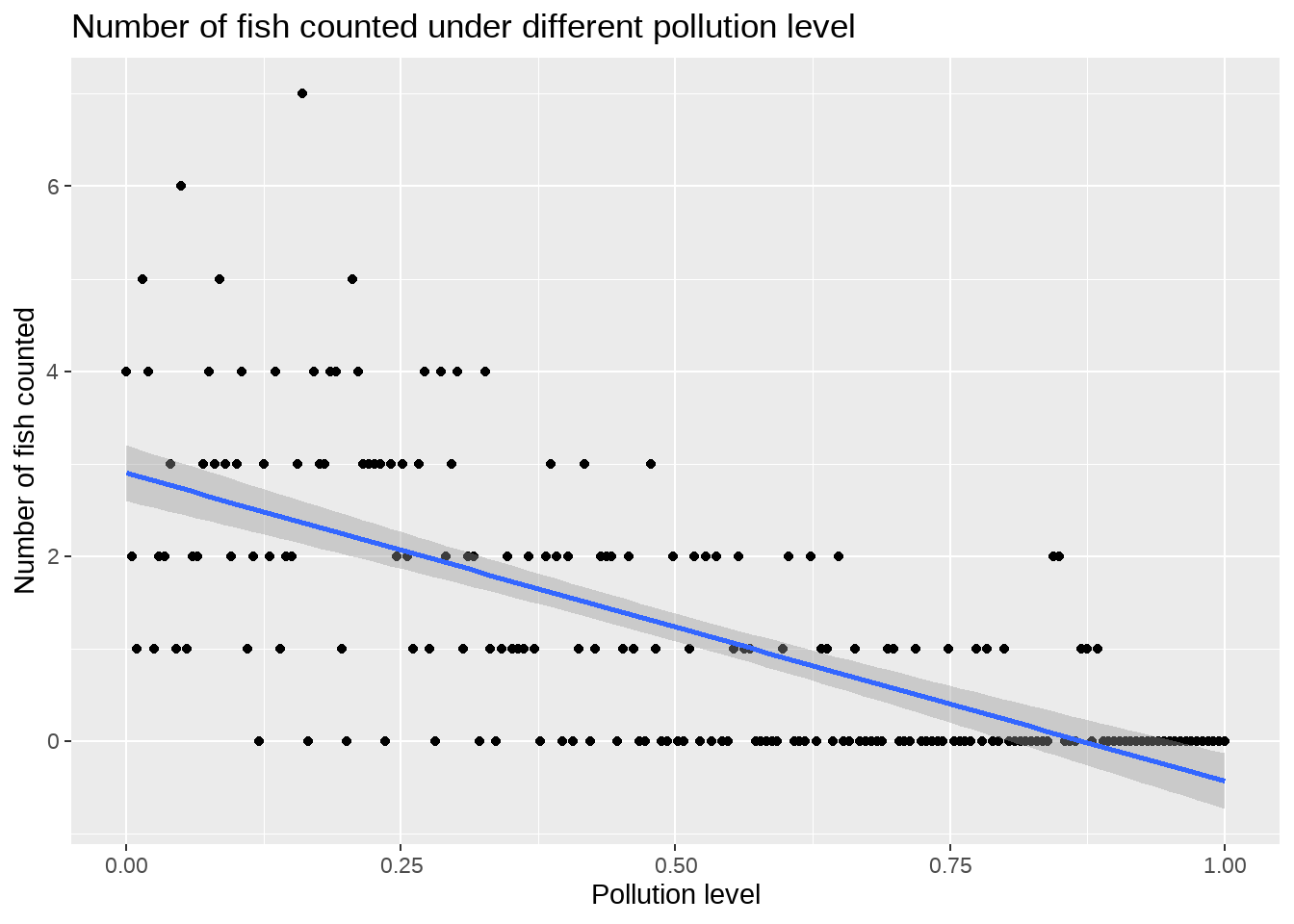
线性关系不明显,而且被解释变量甚至出现了负值。
我们再看看线性模型的结果
##
## Call:
## lm(formula = number_of_fish ~ pollution_level, data = df)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.4986 -0.7088 -0.0237 0.5778 4.6353
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 2.9003 0.1523 19.05 <2e-16 ***
## pollution_level -3.3306 0.2634 -12.65 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.081 on 198 degrees of freedom
## Multiple R-squared: 0.4468, Adjusted R-squared: 0.444
## F-statistic: 159.9 on 1 and 198 DF, p-value: < 2.2e-16线性模型的失灵! 怎么办呢?
58.2.2 泊松分布
我们再看看被解释变量的分布:
- 非负的整数0, 1, 2, 3, 4, …
df %>%
ggplot(aes(x = number_of_fish)) +
geom_histogram() +
labs(
title = "number of fishes (Poisson distribution)"
)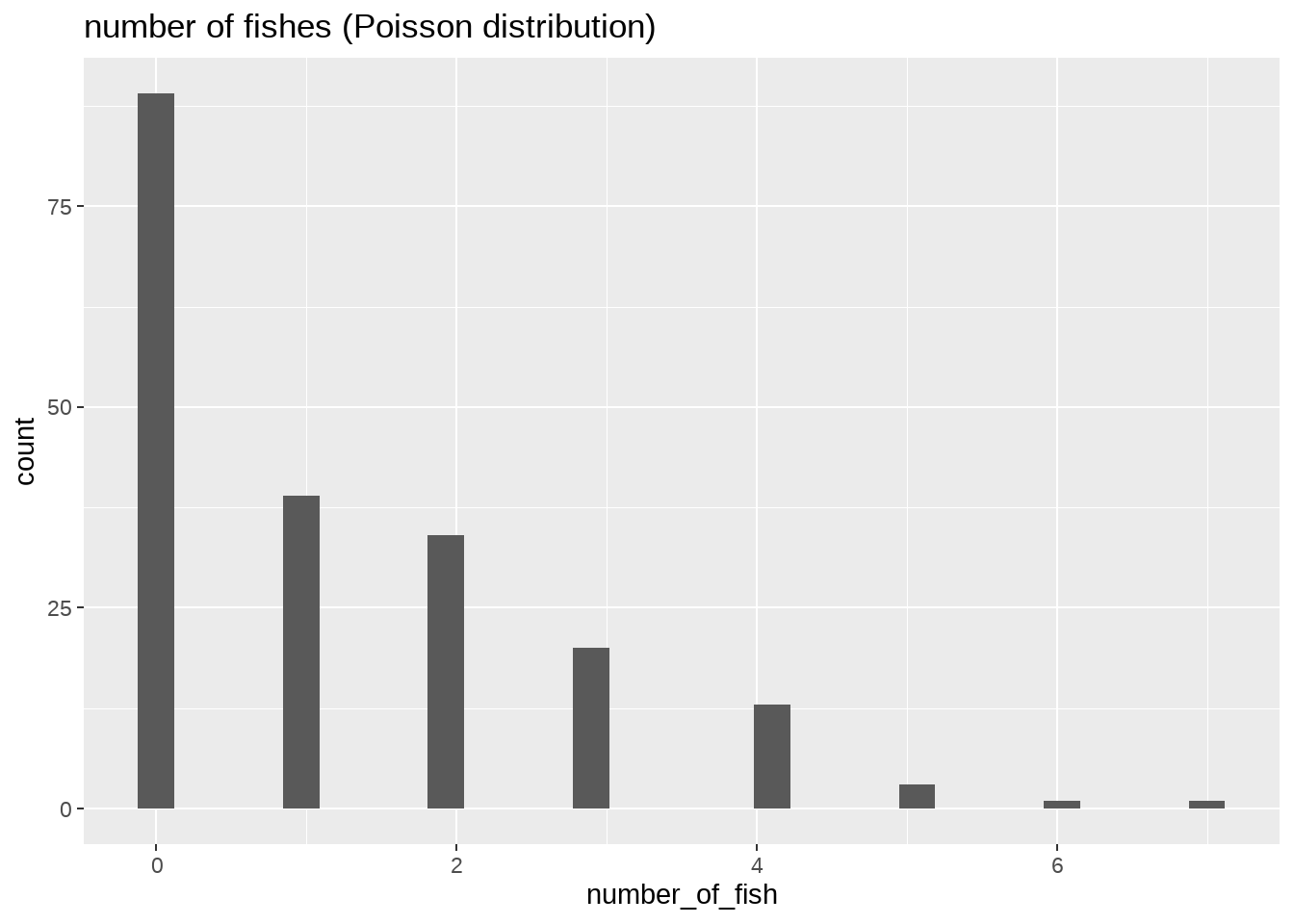
这是典型的泊松分布。
generate_pois <- function(lambda_value) {
tibble(
lambda = as.character(lambda_value),
x = seq(1, 10),
d = dpois(x = x, lambda = lambda_value)
)
}
tb <- seq(0.1, 1.8, by = 0.2) %>% map_dfr(generate_pois)
tb %>%
ggplot(aes(x = x, y = d, color = lambda)) +
geom_point() +
geom_line() +
scale_x_continuous(breaks = seq(1, 10, 1)) +
theme_bw()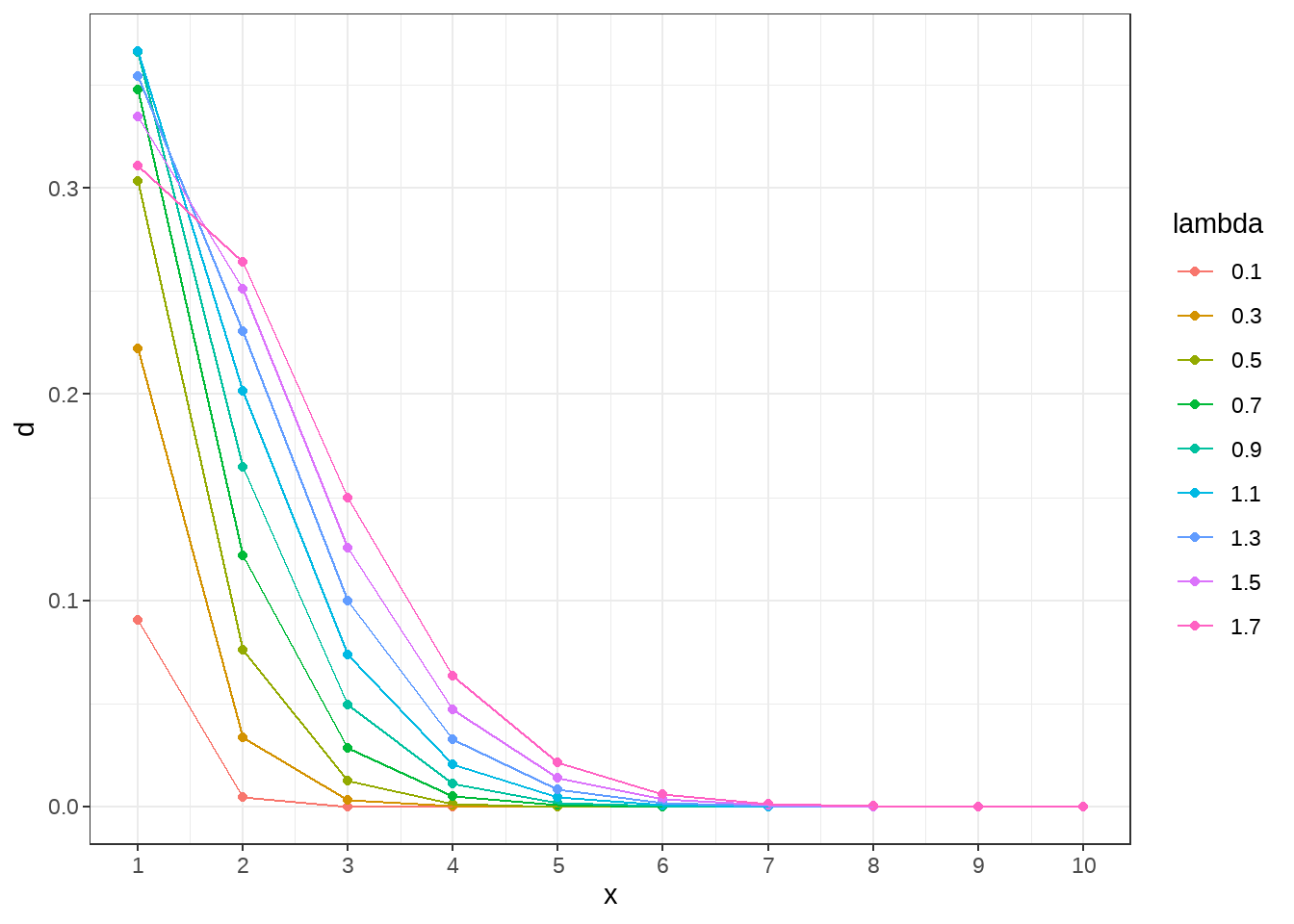
事实上,生活中很多场合都会遇到计数、二进制、yes/no、等待时间等类型的数据,比如
- 医院每天急诊次数
- 每年摩托车死亡人数
- 城市发生火灾的次数
他们有个共同的特征
- 变量代表单位时间或者区域事件发生的次数,服从泊松分布。泊松分布有什么特点?
\[ y_i \sim \text{Poisson}(\lambda = \lambda_i) \]
58.2.3 正态分布换成泊松分布就行了?
回到我们目的:建立不同位置 鱼的数量 与 这个位置的污染程度之间线性关系。
在之前线性模型中讲到,对每一次观测,被解释变量服从正态分布,那么,我们用解释变量的线性组合模拟正态分布的均值\(\mu_i\),即均值\(\mu_i\)随\(x_i\)变化
\[ \begin{align*} y_i \sim & \operatorname{normal}(\mu_i, \, \sigma)\\ &\operatorname{normal}(\mu_i = \beta_0 + \beta_1 x_i, \, \sigma) \end{align*} \]
我们也想如法炮制,正态分布换成泊松分布 \[ \begin{align*} y_i \sim & \text{Poisson}(\lambda_i)\\ & \text{Poisson}(\lambda_i = \beta_0 + \beta_1 x_i) \end{align*} \]
但很遗憾,出现了问题
- 泊松分布的\(\lambda_i\) 要求大于等于0,然而\(\beta_0 + \beta_1 X_i\)势必会出现负数
58.3 泊松回归模型
58.3.1 解决办法-连接函数之美
尽管不能使用直接线性模型,但可以间接使用,统计学家想到用log(\(\lambda_i\)) 代替 \(\lambda_i\),然后让解释变量的线性组合模拟log(\(\lambda_i\)),即 \[ \begin{align*} y_i \sim & \text{Poisson}(\lambda_i)\\ \color{red}\log(\lambda_i) = & \beta_0 + \beta_1 x_i \end{align*} \]
现在问题迎刃而解: - log(\(\lambda_i\)) 值域范围是(\(-\infty\) to \(\infty\)),这样既保证了\(\lambda_i\) 是正值,又保证了\(\beta_0 + \beta_1 x_i\) 可能出现的负值
- 这里的
log()函数就是连接函数, 连接了\(x_i\)和\(\lambda_i\)
所以泊松回归模型为
\[ \begin{align*} \log(\lambda_i) = & \beta_0 + \beta_1 x_i \end{align*} \]
注意到,这里没有线性回归模型中的误差项。通过极大似然估计(Maximum Likelihood Estimation)计算系数\((\beta)\)
什么叫最大相似性估计?通俗点讲,给定y的分布以及独立变量(x)的值,那么最有可能的\(\beta\)系数多是多少?
- step 1 \(y\) 服从泊松分布
\[ \operatorname{Pr}\left(y_{i} | \lambda\right)=\frac{\lambda^{y_{i}} e^{-\lambda}}{y_{i} !}, \quad y=0,1,2, \ldots \quad ; \quad \lambda>0 \]
-
step 2 回归模型 \[ E\left[y_{i} | x_{i}\right]=\lambda_{i}=\exp \left(x_{i}^{\prime} \beta\right) \]
-
step 3 \(\lambda_{i}\) 代入上式,考虑观测值彼此独立,可以将所有\(y_i\)观测值相乘,
\[ \operatorname{Pr}\left(y_{1}, \ldots, y_{N} | x_{1}, \ldots, x_{N}\right)=\prod_{i=1}^{N} \frac{e^{y_{i} x_{i}^{\prime} \beta} e^{-e^{x_{i}^{\prime}} \beta}}{y_{i} !} \]
- step 4 然后取对数,得到(joint log-likelihood function)
\[ l\left(\beta | y_{i}, X_{i}\right)=\sum_{i=1}^{n} y_{i} X_{i}^{\prime} \beta-\exp X_{i}^{\prime} \beta-\log y_{i} ! \]
-
step 5 求偏导 \[ \frac{\partial l}{\partial \beta}=\sum_{i=1}^{n}\left(y_{i}-\exp X_{i}^{\prime} \beta\right) X_{i} \]
-
step 6 令等式等于0,通过样本值,可以求出系数。
58.3.2 代码实现
使用glm()函数:
glm(y ~ 1 + x, family = familytype(link = linkfunction), data = )- formula: 被解释变量 ~ 解释变量
-
family : 误差分布(和连接函数),
family = poisson(link="log") - data : 数据框
##
## Call: glm(formula = number_of_fish ~ pollution_level, family = poisson(link = "log"),
## data = df)
##
## Coefficients:
## (Intercept) pollution_level
## 1.387 -3.108
##
## Degrees of Freedom: 199 Total (i.e. Null); 198 Residual
## Null Deviance: 363
## Residual Deviance: 201.2 AIC: 492.2
summary(m)##
## Call:
## glm(formula = number_of_fish ~ pollution_level, family = poisson(link = "log"),
## data = df)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 1.3872 0.0977 14.20 <2e-16 ***
## pollution_level -3.1077 0.2716 -11.44 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 363.03 on 199 degrees of freedom
## Residual deviance: 201.16 on 198 degrees of freedom
## AIC: 492.22
##
## Number of Fisher Scoring iterations: 5
confint(m)## 2.5 % 97.5 %
## (Intercept) 1.191825 1.574966
## pollution_level -3.651899 -2.586402
broom::tidy(m)## # A tibble: 2 × 5
## term estimate std.error statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 (Intercept) 1.39 0.0977 14.2 9.33e-46
## 2 pollution_level -3.11 0.272 -11.4 2.52e-3058.4 模型解释
我们建立的模型是 \[ \begin{align*} y_i \sim & \text{Poisson}(\lambda_i)\\ \log(\lambda_i) = & \beta_0 + \beta_1 x_i \end{align*} \]
我个人比较喜欢这样写 \[ \begin{align*} y_i \sim & \;\text{Poisson}(\lambda_i = \exp(\beta_0 + \beta_1 x_i)) \end{align*} \]
58.4.1 系数
\[ \begin{align*} \frac{\lambda_1}{\lambda_0} & = \frac{\exp(\beta_1 + \beta_1*x_1)}{\exp(\beta_0 + \beta_1*x_0)} \\ & = \exp(\beta_1(x_1 - x_0)) \end{align*} \]
计算当\(x_i\)增加一个单位时,事件平均发生次数将会是原来的\(\exp(\beta_1)\)倍。具体系数为:
coef(m)## (Intercept) pollution_level
## 1.387188 -3.107740## pollution_level
## 0.04470185## (Intercept) pollution_level
## 4.00357677 0.04470185- 污染系数为0, 4.0035768
- 污染系数从0变到0.5, 引起
(1/exp(-3.1077*0.5) = 4.7)倍数的鱼数量下降. - 污染系数从0变到1, 引起 22.3704397 倍数的鱼数量下降.
58.4.2 边际效应(Marginal effects)
即在其他条件不变的情况下,\(x_i\)增加一个单位,事件的平均发生次数会增加 \(100\beta_1 \%\): 类似求偏导\(\frac{\partial{\lambda}}{\partial{x}}\)
margins::margins(m, type = "link")## pollution_level
## -3.108模型是非线性的,所以我们常用更直观的方式评估边际效应,即,自变量直接对因变量的贡献,可以令type = "response",类似求偏导\(\frac{\partial{y}}{\partial{x}}\)
margins::marginal_effects(m, type = "response", se = TRUE) %>%
as.data.frame() %>%
dplyr::mutate(pollution_level = df$pollution_level) %>%
ggplot(aes(x = pollution_level, y = dydx_pollution_level)) +
geom_point()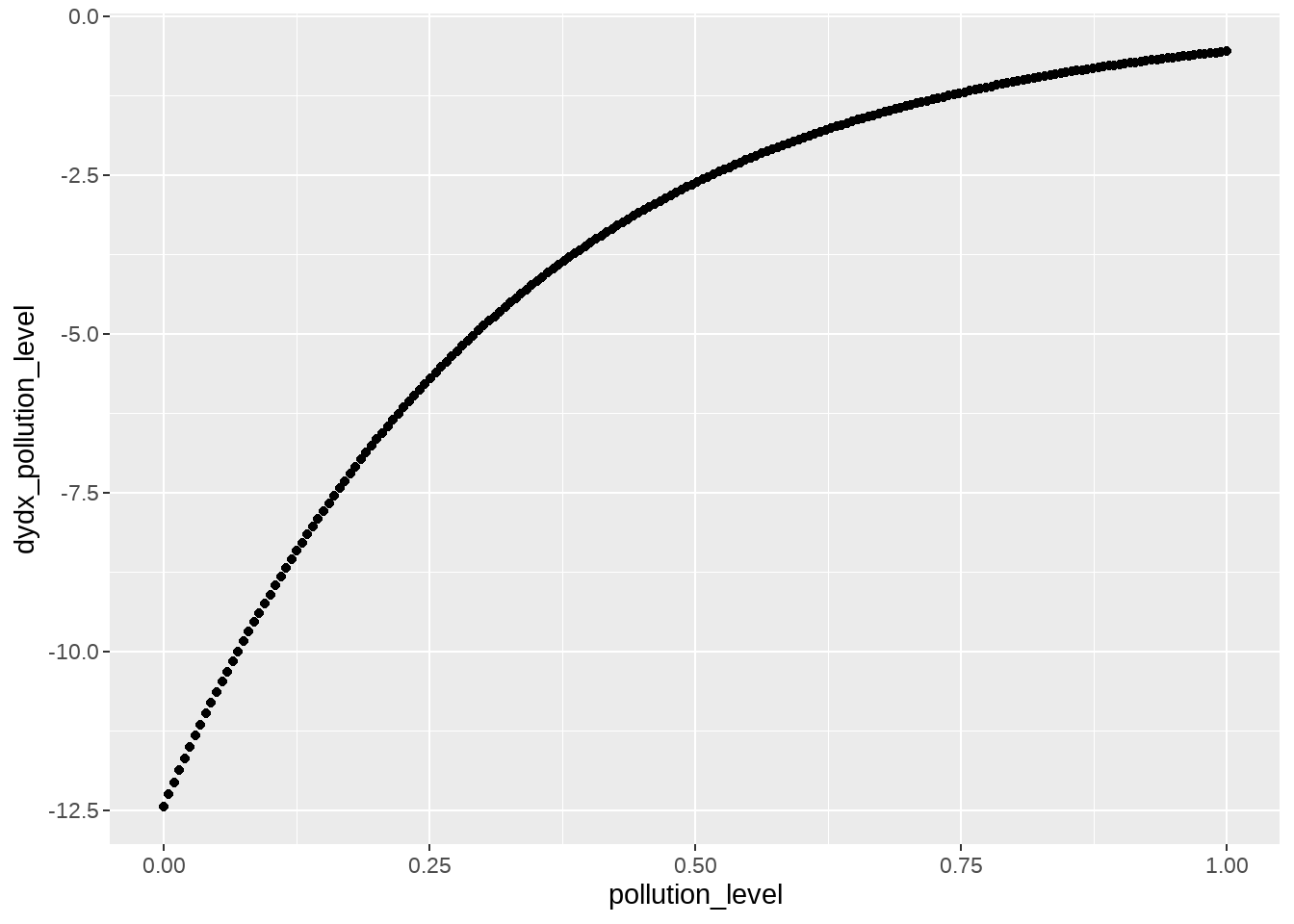
纵坐标是事件的平均发生次数(增加)下降的比例,可以看到随着x变大,下降趋缓。更多边际效应的内容,可参考这里
58.4.3 拟合
## 1 2 3 4 5 6
## 4.003577 3.941539 3.880463 3.820334 3.761136 3.702855实质上就是\(exp(\beta_0 + \beta_1 * pollution_level)\)
intercept <- coef(m)[1]
beta <- coef(m)[2]
df %>%
dplyr::mutate(theory_pred = fitted(m)) %>%
dplyr::mutate(
myguess_pred = exp(intercept + beta * pollution_level)
)## # A tibble: 200 × 4
## pollution_level number_of_fish theory_pred myguess_pred
## <dbl> <int> <dbl> <dbl>
## 1 0 4 4.00 4.00
## 2 0.00503 2 3.94 3.94
## 3 0.0101 1 3.88 3.88
## 4 0.0151 5 3.82 3.82
## 5 0.0201 4 3.76 3.76
## 6 0.0251 1 3.70 3.70
## 7 0.0302 2 3.65 3.65
## 8 0.0352 2 3.59 3.59
## 9 0.0402 3 3.53 3.53
## 10 0.0452 1 3.48 3.48
## # ℹ 190 more rows
df %>%
dplyr::mutate(theory_pred = fitted(m)) %>%
ggplot(aes(x = pollution_level, y = theory_pred)) +
geom_point()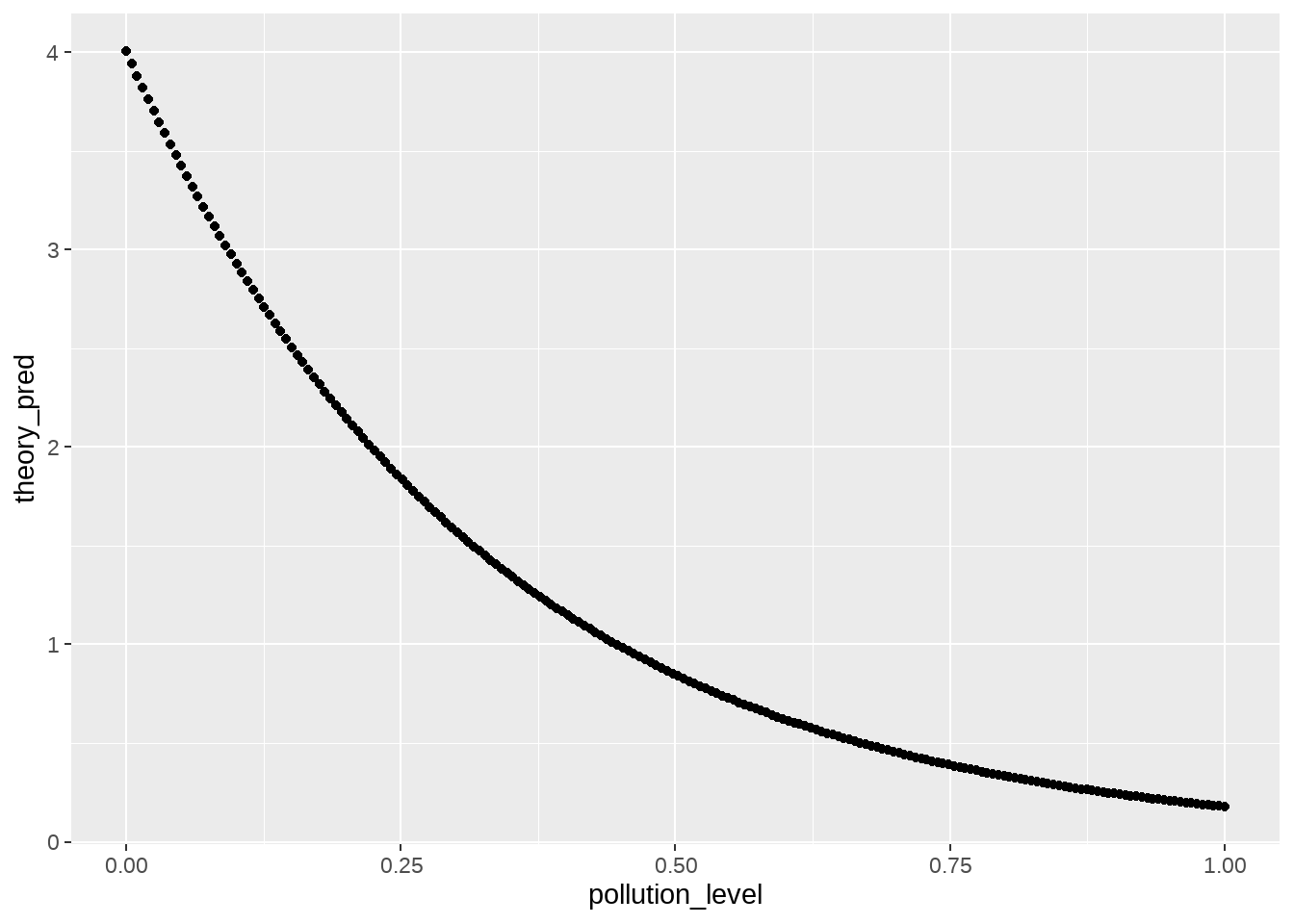
pred <- predict(m, type = "response", se = TRUE) %>% as.data.frame()
pred %>%
head()## fit se.fit residual.scale
## 1 4.003577 0.3911426 1
## 2 3.941539 0.3810162 1
## 3 3.880463 0.3711420 1
## 4 3.820334 0.3615154 1
## 5 3.761136 0.3521314 1
## 6 3.702855 0.3429855 1## # A tibble: 200 × 4
## pollution_level number_of_fish fit se_fit
## <dbl> <int> <dbl> <dbl>
## 1 0 4 4.00 0.391
## 2 0.00503 2 3.94 0.381
## 3 0.0101 1 3.88 0.371
## 4 0.0151 5 3.82 0.362
## 5 0.0201 4 3.76 0.352
## 6 0.0251 1 3.70 0.343
## 7 0.0302 2 3.65 0.334
## 8 0.0352 2 3.59 0.325
## 9 0.0402 3 3.53 0.317
## 10 0.0452 1 3.48 0.309
## # ℹ 190 more rows
real_df <-
tibble(
x = seq(0, 1, length.out = 100),
y = 4 * exp(-3.2 * x)
)
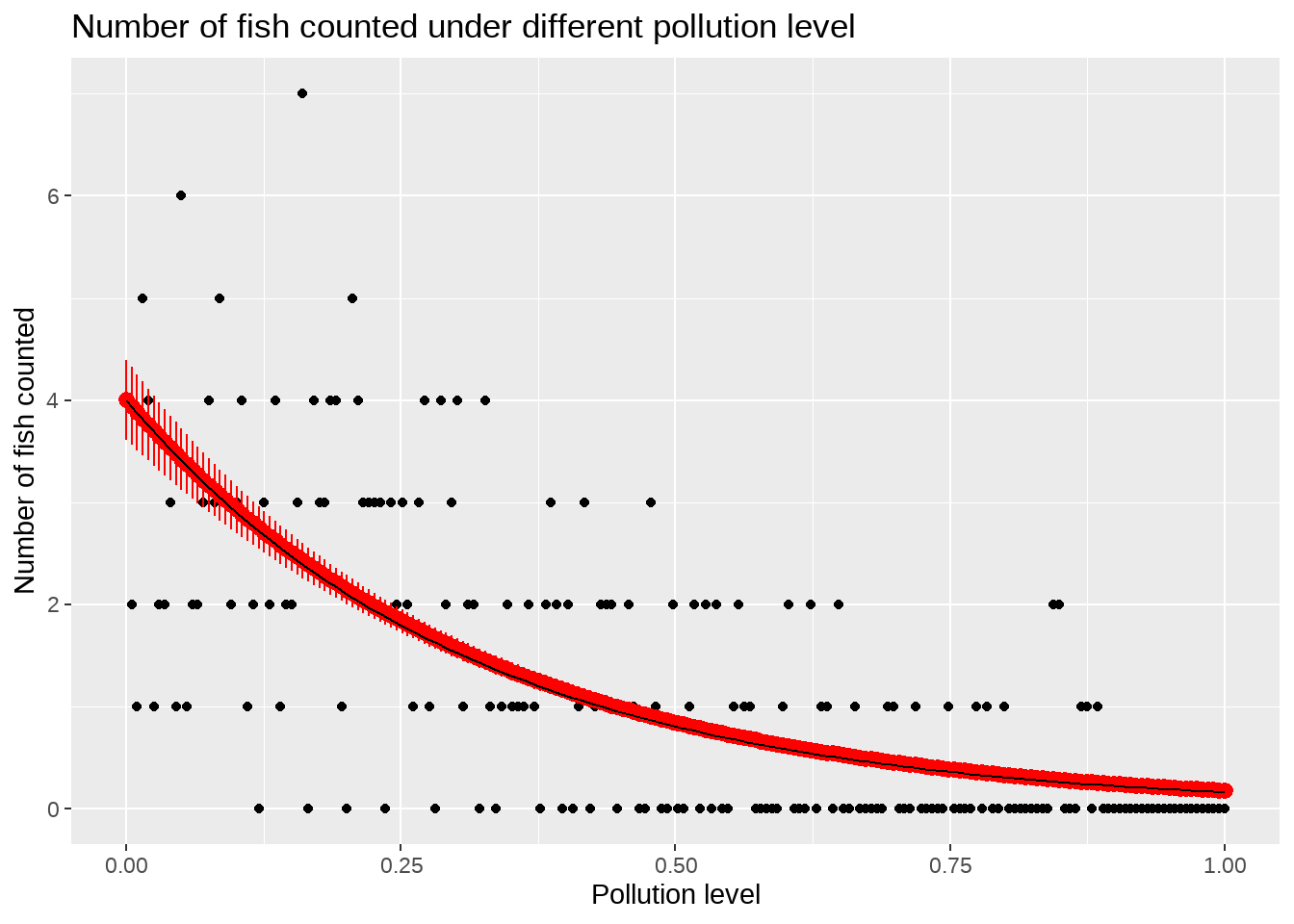
df_pred %>%
ggplot(aes(x = pollution_level, y = number_of_fish)) +
geom_point() +
geom_pointrange(aes(
y = fit,
ymax = fit + se_fit,
ymin = fit - se_fit
), color = "red") +
# geom_point(aes(y = fit + se_fit), color = "red") +
# geom_point(aes(y = fit - se_fit), color = "red") +
geom_line(data = real_df, aes(x = x, y = y), color = "black") +
labs(
title = "Number of fish counted under different pollution level",
x = "Pollution level",
y = "Number of fish counted"
)
58.4.4 模型评估
knitr::include_graphics(path = "images/model_evaluation.png")
- 过度离散,负二项式分布模型
- 零膨胀
margins::margins(m)
ggeffects::ggpredict(m)
ggeffects::ggpredict(m, terms = c("pollution_level"))
performance::model_performance(m)
performance::check_model(m)
performance::check_overdispersion(m)
performance::check_zeroinflation(m)58.5 思考
58.5.1 这两者为什么是相等的?
##
## Call:
## lm(formula = y ~ x, data = d)
##
## Coefficients:
## (Intercept) x
## 4.118 1.996##
## Call: glm(formula = y ~ x, family = gaussian(link = "identity"), data = d)
##
## Coefficients:
## (Intercept) x
## 4.118 1.996
##
## Degrees of Freedom: 99 Total (i.e. Null); 98 Residual
## Null Deviance: 332000
## Residual Deviance: 88.72 AIC: 277.8
lm是glm的一种特殊情形。
58.5.2 log link 与 log transforming
在案例中
- log link
- 先对 number_of_fish 取对数后,然后线性回归
# lm(log(number_of_fish) ~ pollution_level, data = df)
glm(log(number_of_fish) ~ pollution_level,
family = gaussian(link = "identity"),
data = df
)这两者有什么区别?
比较两者的结果,发现有很大的差别,尤其是斜率,为什么呢? 因为这是两个不同的模型:
- 第一个模型中
link="log",模型并没有直接变换数据,只是使用了原始数据的均值,均值对数计算后,建立线性关系,即
\[ \begin{align*} \log(\lambda_i) & = \beta_0 + \beta_1 x_i \\ \lambda_i & = \exp(\beta_0 + \beta_1 x_i) \end{align*} \]
注意到这里family = gaussian, 因此,误差项满足高斯分布
\[ \begin{align*} y_i - \lambda_i &\sim \operatorname{normal}(0,\sigma)\\ y_i - \exp(\beta_0 + \beta_1 x_i) &\sim \operatorname{normal}(0,\sigma) \\ y_i &\sim \operatorname{normal}(\exp(\beta_0 + \beta_1 x_i), \, \sigma) \end{align*} \]
\[ y_i = \exp(\beta_0 + \beta_1 x_i) + \epsilon_i\quad \epsilon_i \sim \operatorname{normal}(0,\sigma) \]
因此对不同均值\(\lambda_i\),误差项的方差是一样的
- 第二个模型
log transforming,是直接转换原始数据,然后建立模型\(\log(y_i) = \alpha + \beta x_i\),原始数据y的均值和方差都改变了,一旦log(y) 变回 y时,
\[ \log(y_i) =\beta_0 + \beta_1 x_i + \epsilon_i, \quad \epsilon_i \sim \operatorname{normal}(0,\sigma) \]
\[ y_i = \exp(\beta_0 + \beta_1 x_i) * \exp(\epsilon_i), \quad \epsilon_i \sim \operatorname{normal}(0,\sigma) \]
误差的方差也会随着均值变化。
58.5.3 更多分布
x <- c(1, 2, 3, 4, 5)
y <- c(1, 2, 4, 2, 6)
regNId <- glm(y ~ x, family = gaussian(link = "identity"))
regNlog <- glm(y ~ x, family = gaussian(link = "log"))
regPId <- glm(y ~ x, family = poisson(link = "identity"))
regPlog <- glm(y ~ x, family = poisson(link = "log"))
regGId <- glm(y ~ x, family = Gamma(link = "identity"))
regGlog <- glm(y ~ x, family = Gamma(link = "log"))
regIGId <- glm(y ~ x, family = inverse.gaussian(link = "identity"))
regIGlog <- glm(y ~ x, family = inverse.gaussian(link = "log"))
dx <- tibble(
x = c(1, 2, 3, 4, 5),
y = c(1, 2, 4, 2, 6)
)
dx %>%
ggplot(aes(x = x, y = y)) +
geom_point()
regNId <- glm(y ~ x, family = gaussian(link = "identity"), data = dx)
regNId
dx %>%
mutate(pred = predict(regNId, type = "response")) %>%
ggplot(aes(x = x, y = y)) +
geom_point() +
geom_line(aes(y = pred, group = 1))