Skip to main content

数据科学中的 R 语言

第 51 章 线性回归

线性模型是数据分析中最常用的一种分析方法。最基础的往往最深刻。

51.1 从一个案例开始

这是一份1994年收集1379个对象关于收入、身高、教育水平等信息的数据集。数据可以在这里下载。

首先，我们下载后导入数据

wages <- read_csv("./demo_data/wages.csv")

wages %>%
  head()
## # A tibble: 6 × 6
##     earn height sex    race     ed   age
##    <dbl>  <dbl> <chr>  <chr> <dbl> <dbl>
## 1 79571.   73.9 male   white    16    49
## 2 96397.   66.2 female white    16    62
## 3 48711.   63.8 female white    16    33
## 4 80478.   63.2 female other    16    95
## 5 82089.   63.1 female white    17    43
## 6 15313.   64.5 female white    15    30

51.1.1 缺失值检查

一般情况下，拿到一份数据，首先要了解数据，知道每个变量的含义，

wages %>% colnames()
## [1] "earn"   "height" "sex"    "race"   "ed"     "age"

同时检查数据是否有缺失值，这点很重要。在R中 NA（not available，不可用）表示缺失值, 比如可以这样检查是否有缺失值。

wages %>%
  summarise(
    earn_na   = sum(is.na(earn)),
    height_na = sum(is.na(height)),
    sex_na    = sum(is.na(sex)),
    race_na   = sum(is.na(race)),
    ed_na     = sum(is.na(ed)),
    age_na    = sum(is.na(age))
  )
## # A tibble: 1 × 6
##   earn_na height_na sex_na race_na ed_na age_na
##     <int>     <int>  <int>   <int> <int>  <int>
## 1       0         0      0       0     0      0

程序员都是偷懒的，所以也可以写的简便一点。大家在学习的过程中，也会慢慢的发现tidyverse的函数很贴心，很周到。

wages %>%
  summarise_all(
    ~ sum(is.na(.))
  )
## # A tibble: 1 × 6
##    earn height   sex  race    ed   age
##   <int>  <int> <int> <int> <int> <int>
## 1     0      0     0     0     0     0

当然，也可以用purrr::map()的方法。这部分我会在后面的章节中逐步介绍。

wages %>%
  map_df(~ sum(is.na(.)))
## # A tibble: 1 × 6
##    earn height   sex  race    ed   age
##   <int>  <int> <int> <int> <int> <int>
## 1     0      0     0     0     0     0

51.1.2 变量简单统计

然后探索下每个变量的分布。比如调研数据中男女的数量分别是多少？

wages %>% count(sex)
## # A tibble: 2 × 2
##   sex        n
##   <chr>  <int>
## 1 female   859
## 2 male     520

男女这两组的身高均值分别是多少？收入的均值分别是多少？

wages %>%
  group_by(sex) %>%
  summarise(
    n = n(),
    mean_height = mean(height),
    mean_earn = mean(earn)
  )
## # A tibble: 2 × 4
##   sex        n mean_height mean_earn
##   <chr>  <int>       <dbl>     <dbl>
## 1 female   859        64.5    24246.
## 2 male     520        70.0    45993.

也有可以用可视化的方法，呈现男女收入的分布情况

wages %>%
  ggplot(aes(x = earn, color = sex)) +
  geom_density()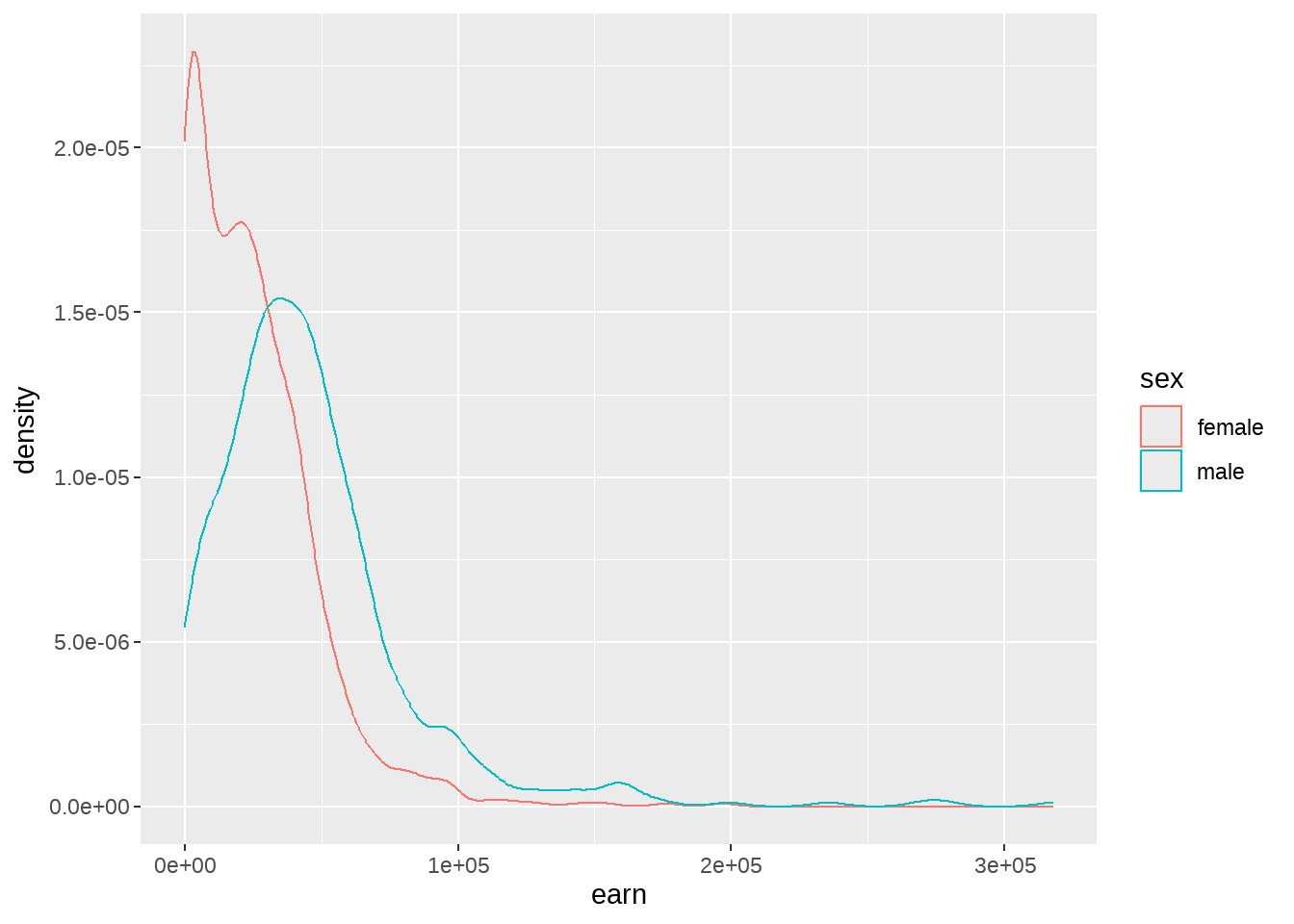

大家可以自行探索其他变量的情况。现在提出几个问题，希望大家带着这些问题去探索：

  1. 长的越高的人挣钱越多？

  2. 是否男性就比女性挣的多？

  3. 影响收入最大的变量是哪个？

  4. 怎么判定我们建立的模型是不是很好？

51.2 线性回归模型

长的越高的人挣钱越多？

要回答这个问题，我们先介绍线性模型。顾名思义，就是认为\(x\)和\(y\)之间有线性关系，数学上可以写为

\[ \begin{aligned} y &= \alpha + \beta x + \epsilon \\ \epsilon &\in \text{Normal}(\mu, \sigma) \end{aligned} \]

\(\epsilon\) 代表误差项，它与\(x\) 无关，且服从正态分布。 建立线性模型，就是要估计这里的系数\(\hat\alpha\)和\(\hat\beta\)，即截距项和斜率项。常用的方法是最小二乘法（ordinary least squares (OLS) regression）： 就是我们估算的\(\hat\alpha\)和\(\hat\beta\), 要使得残差的平方和最小，即\(\sum_i(y_i - \hat y_i)^2\)或者叫\(\sum_i \epsilon_i^2\)最小。

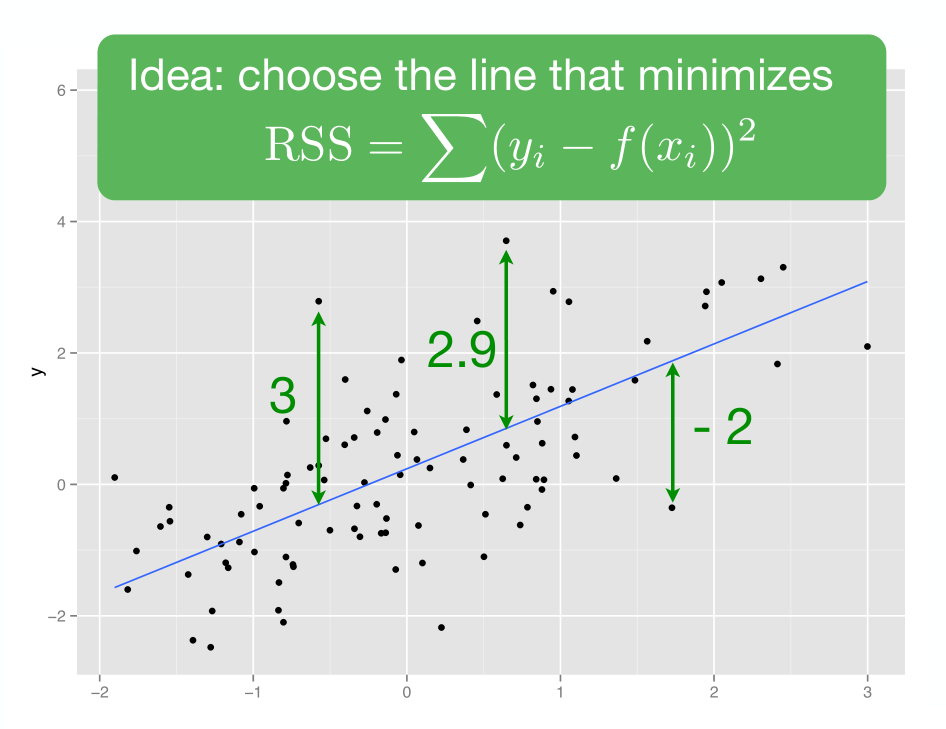
当然，数据量很大，手算是不现实的，我们借助R语言代码吧

51.3 使用lm() 函数

用R语言代码(建议大家先?lm看看帮助文档)，

lm参数很多, 但很多我们都用不上，所以我们只关注其中重要的两个参数

lm(formula = y ~ x, data)

lm(y ~ x, data) 是最常用的线性模型函数(lm是linear model的缩写)。参数解释说明

  • formula：指定回归模型的公式，对于简单的线性回归模型y ~ x.
  • ~ 符号：代表“预测”，可以读做“y由x预测”。有些学科不同的表述，比如下面都是可以的
    • response ~ explanatory
    • dependent ~ independent
    • outcome ~ predictors
  • data：代表数据框，数据框包含了响应变量和独立变量

在运行lm()之前，先画出身高和收入的散点图(记在我们想干什么，寻找身高和收入的关系)

wages %>%
  ggplot(aes(x = height, y = earn)) +
  geom_point()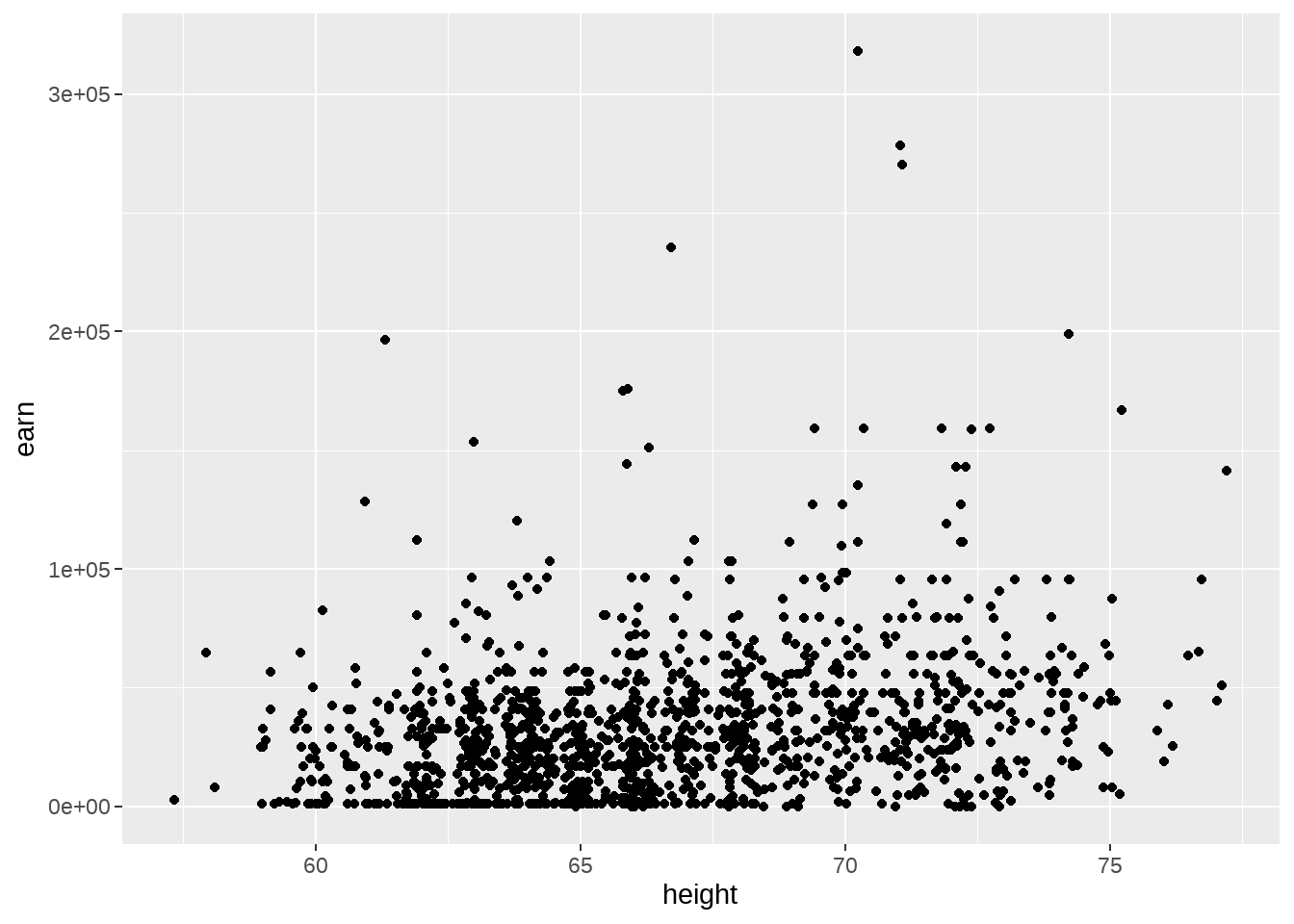

等不及了，就运行代码吧

mod1 <- lm(
  formula = earn ~ height,
  data = wages
)

这里我们将earn作为响应变量，height为预测变量。lm()返回赋值给mod1. mod1现在是个什么东东呢？ mod1是一个叫lm object或者叫类的东西，

names(mod1)
##  [1] "coefficients"  "residuals"     "effects"       "rank"         
##  [5] "fitted.values" "assign"        "qr"            "df.residual"  
##  [9] "xlevels"       "call"          "terms"         "model"

我们打印看看，会发生什么

print(mod1)
## 
## Call:
## lm(formula = earn ~ height, data = wages)
## 
## Coefficients:
## (Intercept)       height  
##     -126523         2387

这里有两部分信息。首先第一部分是我们建立的模型；第二部分是R给出了截距（\(\alpha = -126532\)）和斜率（\(\beta = 2387\)）. 也就是说我们建立的线性回归模型是 \[ \hat y = -126532 + 2387 \; x \]

查看详细信息

summary(mod1)
## 
## Call:
## lm(formula = earn ~ height, data = wages)
## 
## Residuals:
##    Min     1Q Median     3Q    Max 
## -47903 -19744  -5184  11642 276796 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  -126523      14076  -8.989   <2e-16 ***
## height          2387        211  11.312   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 29910 on 1377 degrees of freedom
## Multiple R-squared:  0.08503,    Adjusted R-squared:  0.08437 
## F-statistic:   128 on 1 and 1377 DF,  p-value: < 2.2e-16

查看拟合值

# predict(mod1) # predictions at original x values
wages %>% modelr::add_predictions(mod1)
## # A tibble: 1,379 × 7
##      earn height sex    race        ed   age   pred
##     <dbl>  <dbl> <chr>  <chr>    <dbl> <dbl>  <dbl>
##  1 79571.   73.9 male   white       16    49 49867.
##  2 96397.   66.2 female white       16    62 31581.
##  3 48711.   63.8 female white       16    33 25708.
##  4 80478.   63.2 female other       16    95 24395.
##  5 82089.   63.1 female white       17    43 24061.
##  6 15313.   64.5 female white       15    30 27522.
##  7 47104.   61.5 female white       12    53 20385.
##  8 50960.   73.3 male   white       17    50 48434.
##  9  3213.   72.2 male   hispanic    15    25 45928.
## 10 42997.   72.4 male   white       12    30 46310.
## # ℹ 1,369 more rows

查看残差值

# resid(mod1)
wages %>%
  modelr::add_predictions(mod1) %>%
  modelr::add_residuals(mod1)
## # A tibble: 1,379 × 8
##      earn height sex    race        ed   age   pred   resid
##     <dbl>  <dbl> <chr>  <chr>    <dbl> <dbl>  <dbl>   <dbl>
##  1 79571.   73.9 male   white       16    49 49867.  29705.
##  2 96397.   66.2 female white       16    62 31581.  64816.
##  3 48711.   63.8 female white       16    33 25708.  23003.
##  4 80478.   63.2 female other       16    95 24395.  56083.
##  5 82089.   63.1 female white       17    43 24061.  58028.
##  6 15313.   64.5 female white       15    30 27522. -12209.
##  7 47104.   61.5 female white       12    53 20385.  26720.
##  8 50960.   73.3 male   white       17    50 48434.   2526.
##  9  3213.   72.2 male   hispanic    15    25 45928. -42715.
## 10 42997.   72.4 male   white       12    30 46310.  -3313.
## # ℹ 1,369 more rows

51.4 模型的解释

建立一个lm模型是简单的，然而最重要的是，我们能解释这个模型。

mod1的解释：

  • 对于斜率\(\beta = 2387\)意味着，当一个人的身高是68英寸时，他的预期收入\(earn = -126532 + 2387 \times 68= 35806\) 美元， 换个方式说，身高\(height\)每增加一个1英寸, 收入\(earn\)会增加2387美元。

  • 对于截距\(\alpha = -126532\)，即当身高为0时，期望的收入值-126532。呵呵，人的身高不可能为0，所以这是一种极端的理论情况，现实不可能发生。

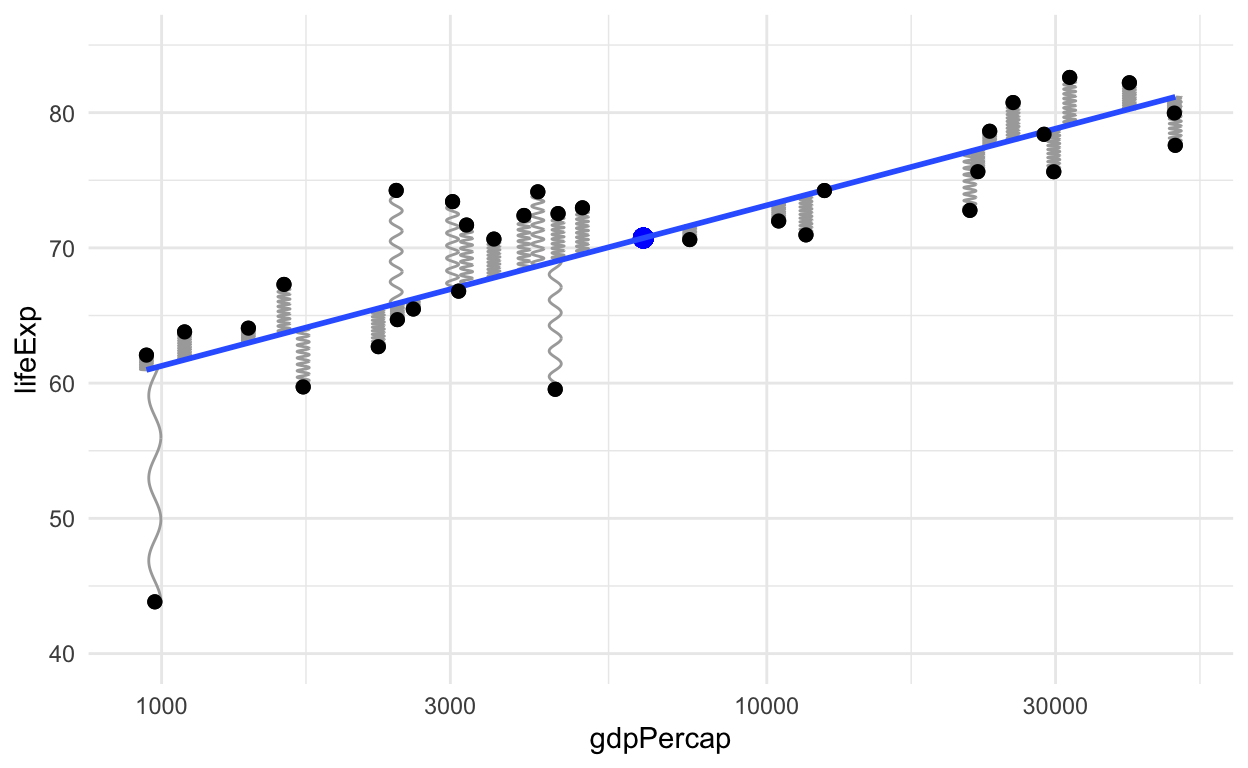
wages %>%
  ggplot(aes(x = height, y = earn)) +
  geom_point(alpha = 0.25) +
  geom_smooth(method = "lm", se = FALSE)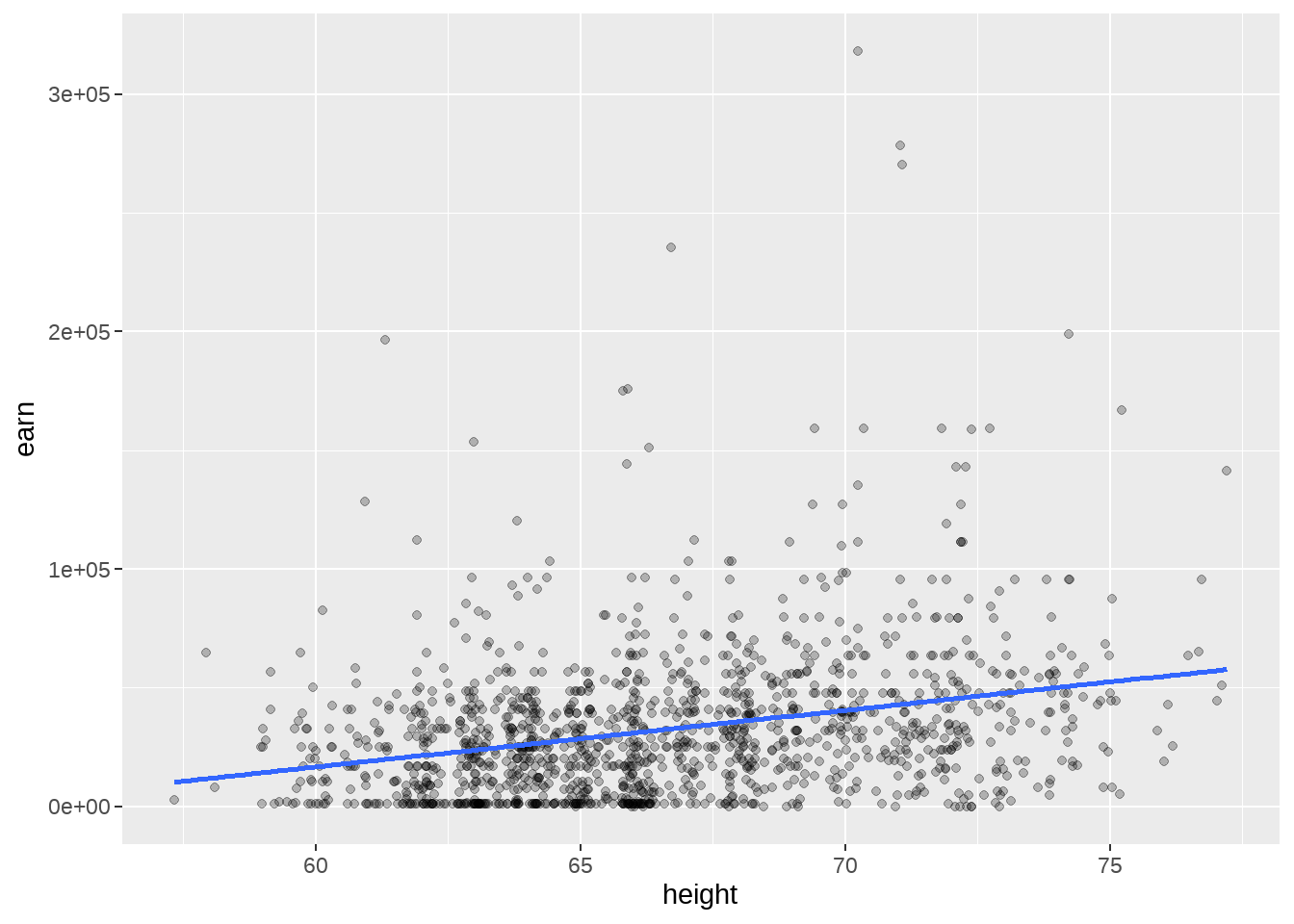

51.5 多元线性回归

刚才讨论的单个预测变量height，现在我们增加一个预测变量ed，稍微扩展一下我们的一元线性模型，就是多元回归模型

\[ \begin{aligned} earn &= \alpha + \beta_1 \text{height} + \beta_2 \text{ed} +\epsilon \\ \end{aligned} \]

R语言代码实现也很简单，只需要把变量ed增加在公式的右边

mod2 <- lm(earn ~ height + ed, data = wages)

同样，我们打印mod2看看

mod2
## 
## Call:
## lm(formula = earn ~ height + ed, data = wages)
## 
## Coefficients:
## (Intercept)       height           ed  
##     -161541         2087         4118

大家试着解释下mod2. 😄

51.6 更多模型 

lm(earn ~ sex, data = wages)
lm(earn ~ ed, data = wages)
lm(earn ~ age, data = wages)

lm(earn ~ height + sex, data = wages)
lm(earn ~ height + ed, data = wages)
lm(earn ~ height + age, data = wages)
lm(earn ~ height + race, data = wages)


lm(earn ~ height + sex + ed, data = wages)
lm(earn ~ height + sex + age, data = wages)
lm(earn ~ height + sex + race, data = wages)
lm(earn ~ height + ed + age, data = wages)
lm(earn ~ height + ed + race, data = wages)
lm(earn ~ height + age + race, data = wages)

lm(earn ~ height + sex + ed + age, data = wages)
lm(earn ~ height + sex + ed + race, data = wages)
lm(earn ~ height + sex + age + race, data = wages)
lm(earn ~ height + ed + age + race, data = wages)
lm(earn ~ sex + ed + age + race, data = wages)

lm(earn ~ height + sex + ed + age + race, data = wages)

51.7 变量重要性

哪个变量对收入的影响最大？

lm(earn ~ height + ed + age, data = wages)
  • 方法一，变量都做标准化处理后，再放到模型中计算，然后对比系数的绝对值
fit <- wages %>%
  mutate_at(vars(earn, height, ed, age), scale) %>%
  lm(earn ~ 1 + height + ed + age, data = .)

summary(fit)
## 
## Call:
## lm(formula = earn ~ 1 + height + ed + age, data = .)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -1.9213 -0.5356 -0.1206  0.3525  8.2982 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -1.768e-16  2.396e-02    0.00        1    
## height       2.736e-01  2.430e-02   11.26  < 2e-16 ***
## ed           3.392e-01  2.429e-02   13.97  < 2e-16 ***
## age          1.546e-01  2.435e-02    6.35 2.92e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.8897 on 1375 degrees of freedom
## Multiple R-squared:  0.2101, Adjusted R-squared:  0.2084 
## F-statistic: 121.9 on 3 and 1375 DF,  p-value: < 2.2e-16
caret::varImp(fit)
##          Overall
## height 11.257099
## ed     13.965858
## age     6.349786

51.8 可能遇到的情形

根据同学们的建议，模型中涉及统计知识，留给统计老师讲，我们这里是R语言课，应该讲代码。 因此，这里再介绍几种线性回归中遇到的几种特殊情况

51.8.1 截距项

包含截距，以下两者是等价的

lm(earn ~ 1 + height, data = wages)
lm(earn ~ height, data = wages)

去掉截距，以下两者是等价的

lm(earn ~ height - 1, data = wages)
lm(earn ~ 0 + height, data = wages)

不包含截距项，实际上就是强制通过原点(0,0)，这样做很大程度上影响了斜率。

51.8.2 只有截距项 

lm(earn ~ 1, data = wages)
## 
## Call:
## lm(formula = earn ~ 1, data = wages)
## 
## Coefficients:
## (Intercept)  
##       32446

只有截距项，实质上就是计算y变量的均值

wages %>%
  summarise(
    mean_wages = mean(earn)
  )
## # A tibble: 1 × 1
##   mean_wages
##        <dbl>
## 1     32446.

51.8.3 分类变量

race变量就是数据框wages的一个分类变量，代表四个不同的种族。用分类变量做回归，本质上是各组之间的进行比较。

wages %>% distinct(race)
## # A tibble: 4 × 1
##   race    
##   <chr>   
## 1 white   
## 2 other   
## 3 hispanic
## 4 black
wages %>%
  ggplot(aes(x = race, y = earn, fill = race)) +
  geom_boxplot(position = position_dodge()) +
  scale_y_continuous(limits = c(0, 20000))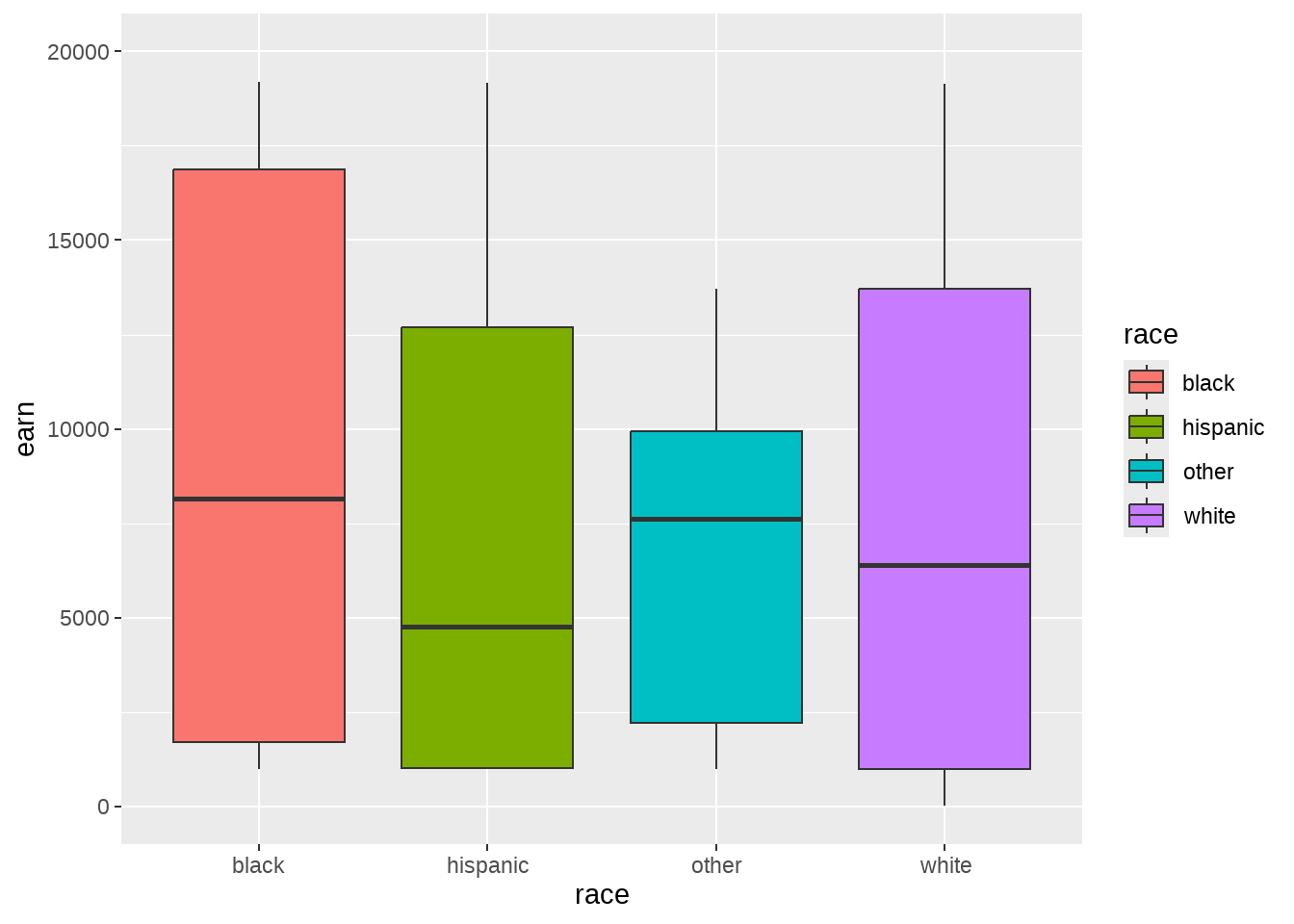

以分类变量作为解释变量，做线性回归

mod3 <- lm(earn ~ race, data = wages)
mod3
## 
## Call:
## lm(formula = earn ~ race, data = wages)
## 
## Coefficients:
##  (Intercept)  racehispanic     raceother     racewhite  
##        28372         -2887          3905          4993

tidyverse框架下，喜欢数据框的统计结果，因此，可用broom的tidy()函数将模型输出转换为数据框的形式

broom::tidy(mod3)
## # A tibble: 4 × 5
##   term         estimate std.error statistic  p.value
##   <chr>           <dbl>     <dbl>     <dbl>    <dbl>
## 1 (Intercept)    28372.     2781.    10.2   1.29e-23
## 2 racehispanic   -2887.     4515.    -0.639 5.23e- 1
## 3 raceother       3905.     6428.     0.608 5.44e- 1
## 4 racewhite       4993.     2929.     1.70  8.85e- 2

我们看到输出结果，只有race_hispanic、 race_other和race_white三个系数和Intercept截距，race_black去哪里了呢？

事实上，race变量里有4组，回归时，选择black为基线，hispanic的系数，可以理解为由black切换到hispanic，引起earn收入的变化（效应）

  • 对 black 组的估计，earn = 28372.09 = 28372.09
  • 对 hispanic组的估计，earn = 28372.09 + -2886.79 = 25485.30
  • 对 other 组的估计，earn = 28372.09 + 3905.32 = 32277.41
  • 对 white 组的估计，earn = 28372.09 + 4993.33 = 33365.42

分类变量的线性回归本质上就是方差分析

第 54章专题讨论方差分析

51.8.4 因子变量

hispanic组的估计最低，适合做基线，因此可以将race转换为因子变量，这样方便调整因子先后顺序

wages_fct <- wages %>%
  mutate(race = factor(race, levels = c("hispanic", "white", "black", "other"))) %>%
  select(earn, race)

head(wages_fct)
## # A tibble: 6 × 2
##     earn race 
##    <dbl> <fct>
## 1 79571. white
## 2 96397. white
## 3 48711. white
## 4 80478. other
## 5 82089. white
## 6 15313. white

wages_fct替换wages，然后建立线性模型

mod4 <- lm(earn ~ race, data = wages_fct)
broom::tidy(mod4)
## # A tibble: 4 × 5
##   term        estimate std.error statistic  p.value
##   <chr>          <dbl>     <dbl>     <dbl>    <dbl>
## 1 (Intercept)   25485.     3557.     7.16  1.26e-12
## 2 racewhite      7880.     3674.     2.14  3.22e- 2
## 3 raceblack      2887.     4515.     0.639 5.23e- 1
## 4 raceother      6792.     6800.     0.999 3.18e- 1

以hispanic组作为基线，各组系数也调整了，但加上截距后，实际值是没有变的。

大家可以用sex变量试试看

lm(earn ~ sex, data = wages)

51.8.5 一个分类变量和一个连续变量

如果预测变量是一个分类变量和一个连续变量

mod5 <- lm(earn ~ height + sex, data = wages)
coef(mod5)
## (Intercept)      height     sexmale 
##  -32479.861     879.424   16874.158
  • height = 879.424 当sex保持不变时，height变化引起的earn变化
  • sexmale = 16874.158 当height保持不变时，sex变化(female变为male)引起的earn变化
p1 <- wages %>%
  ggplot(aes(x = height, y = earn, color = sex)) +
  geom_point(alpha = 0.1) +
  geom_line(aes(y = predict(mod5))) +
  coord_cartesian(ylim = c(0, 100000))
p1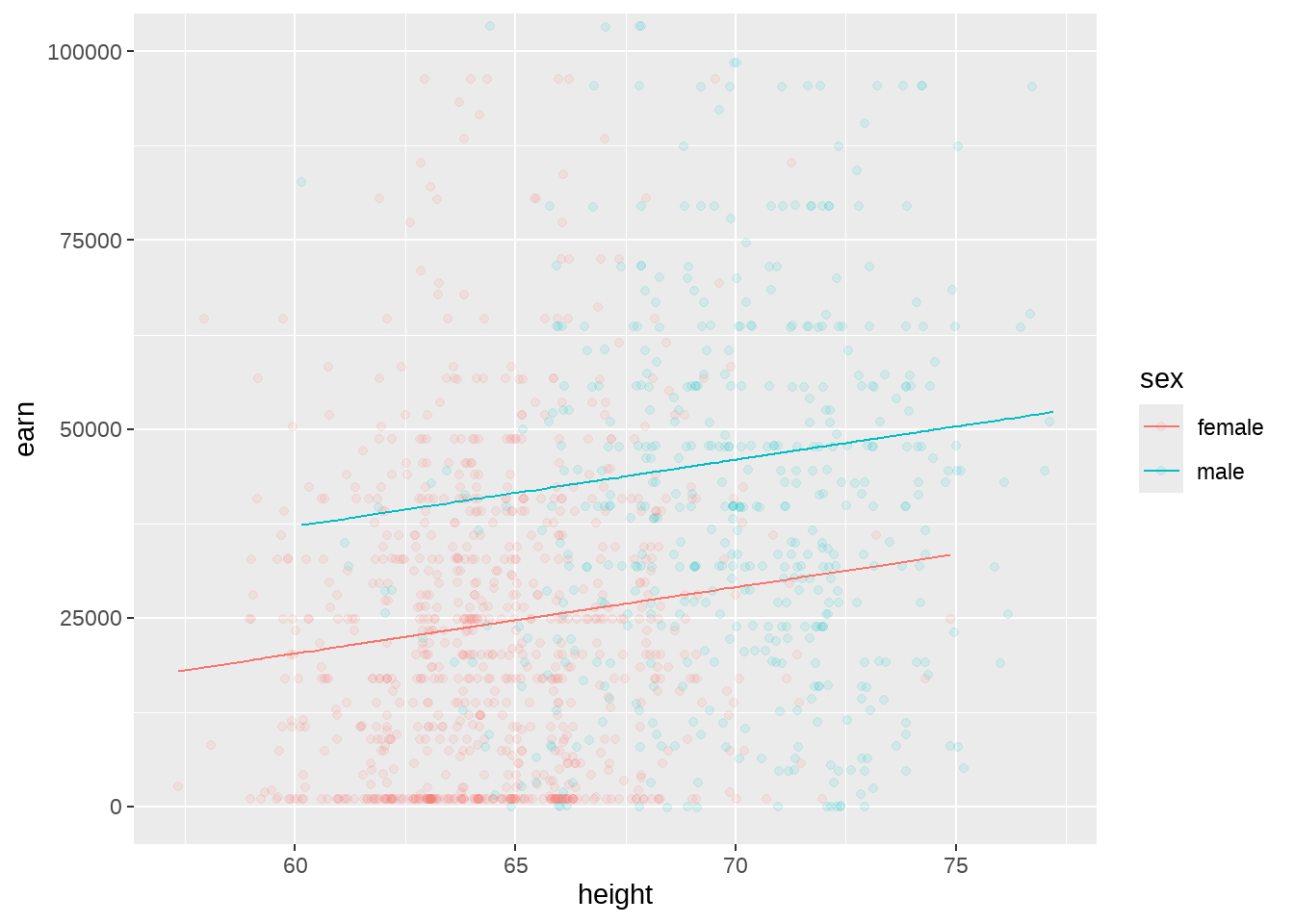

51.8.6 偷懒的写法

. is shorthand for “everything else.”

lm(earn ~ height + sex + race + ed + age, data = wages)
lm(earn ~ ., data = wages)

lm(earn ~ height + sex + race + ed, data = wages)
lm(earn ~ . - age, data = wages)

R 语言很多时候都出现了.，不同的场景，含义是不一样的。我会在后面第 46 章专门讨论这个问题， 这是一个非常重要的问题

51.8.7 交互项 

lm(earn ~ height + sex + height:sex, data = wages)
lm(earn ~ height * sex, data = wages)
lm(earn ~ (height + sex)^2, data = wages)
lm(earn ~ height:sex, data = wages)
lm(earn ~ height:sex:race, data = wages)
mod6 <- lm(earn ~ height + sex + height:sex, data = wages)
coef(mod6)
##    (Intercept)         height        sexmale height:sexmale 
##    -12166.9667       564.5102    -30510.4336       701.4065
  • 对于女性，height增长1个单位，引起earn的增长564.5102
  • 对于男性，height增长1个单位，引起earn的增长564.5102 + 701.4065 = 1265.92 
p2 <- wages %>%
  ggplot(aes(x = height, y = earn, color = sex)) +
  geom_point(alpha = 0.1) +
  geom_line(aes(y = predict(mod6))) +
  coord_cartesian(ylim = c(0, 100000))
p2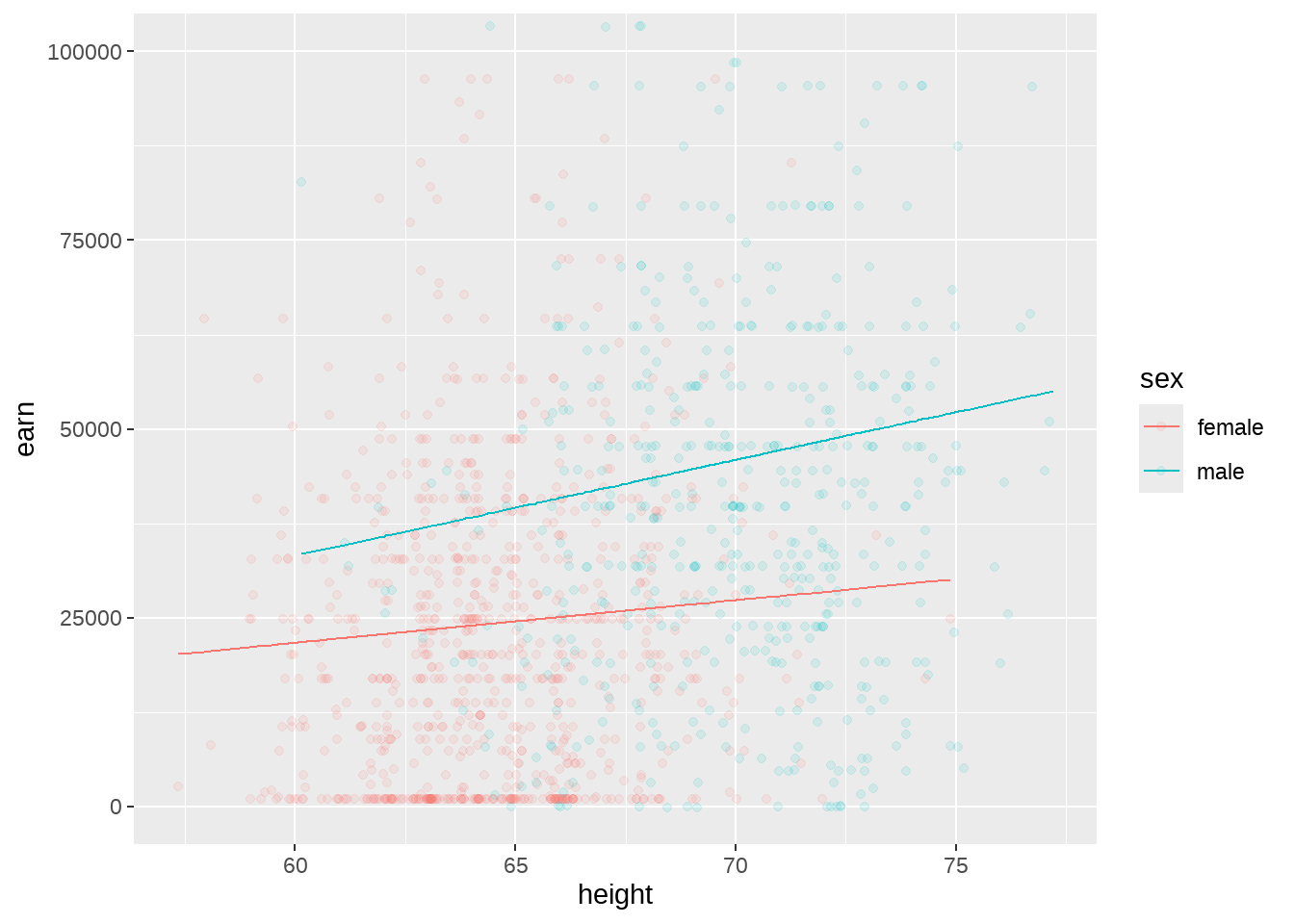

注意，没有相互项和有相互项的区别

library(patchwork)

combined <- p1 + p2 & theme(legend.position = "bottom")
combined + plot_layout(guides = "collect")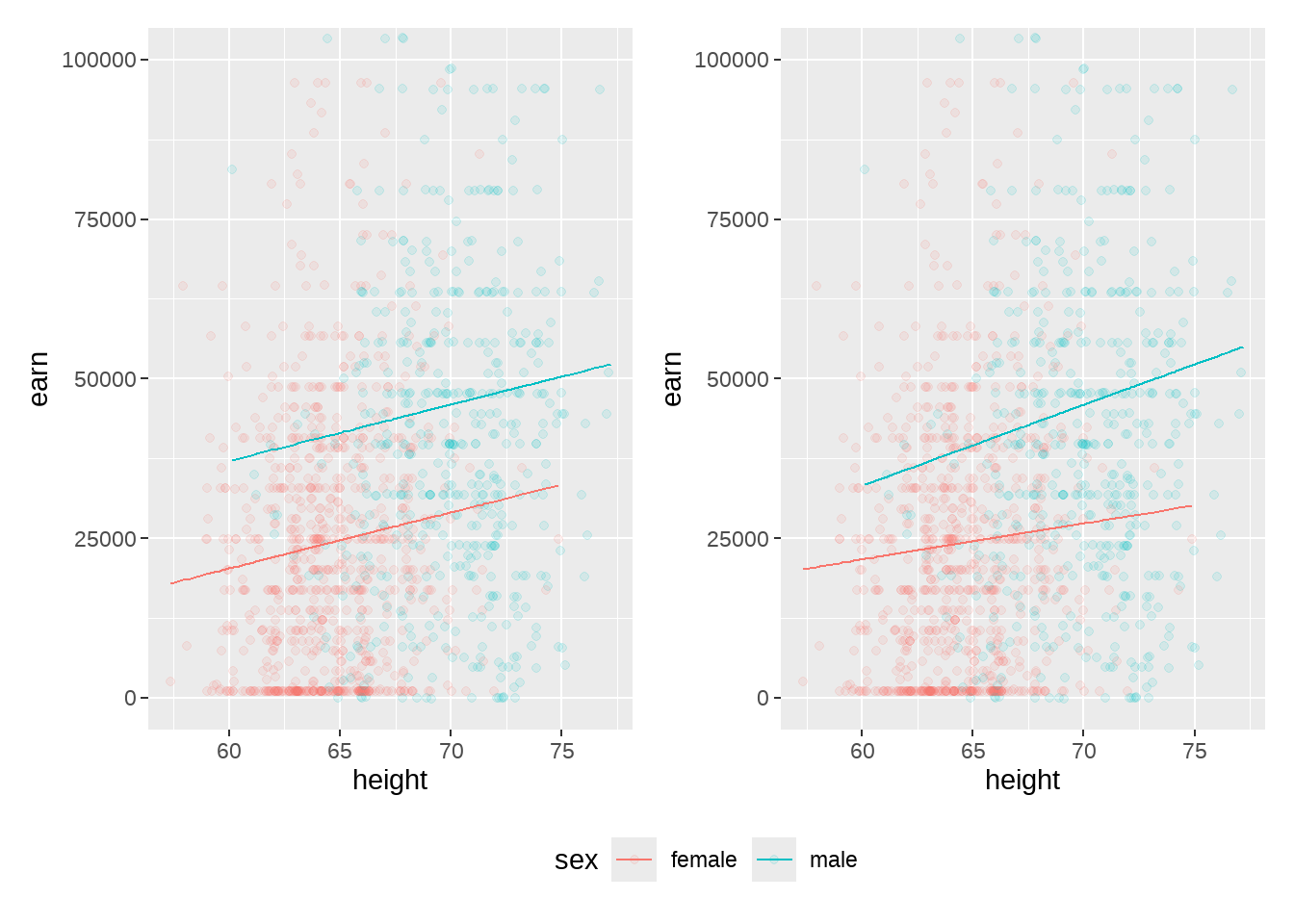

51.8.8 虚拟变量

交互项，有点不好理解？我们再细致说一遍

earn ~ height + sex + height:sex

对应的数学表达式 \[ \begin{aligned} \text{earn} &= \alpha + \beta_1 \text{height} + \beta_2 \text{sex} +\beta_3 \text{(height*sex)}+ \epsilon \\ \end{aligned} \]

我们要求出其中的\(\alpha, \beta_1, \beta_2, \beta_3\)，事实上，分类变量在R语言代码里，会转换成0和1这种虚拟变量，然后再计算。类似

wages %>% mutate(sexmale = if_else(sex == "female", 0, 1))
## # A tibble: 1,379 × 7
##      earn height sex    race        ed   age sexmale
##     <dbl>  <dbl> <chr>  <chr>    <dbl> <dbl>   <dbl>
##  1 79571.   73.9 male   white       16    49       1
##  2 96397.   66.2 female white       16    62       0
##  3 48711.   63.8 female white       16    33       0
##  4 80478.   63.2 female other       16    95       0
##  5 82089.   63.1 female white       17    43       0
##  6 15313.   64.5 female white       15    30       0
##  7 47104.   61.5 female white       12    53       0
##  8 50960.   73.3 male   white       17    50       1
##  9  3213.   72.2 male   hispanic    15    25       1
## 10 42997.   72.4 male   white       12    30       1
## # ℹ 1,369 more rows

那么上面的公式变为 \[ \begin{aligned} \text{earn} &= \alpha + \beta_1 \text{height} + \beta_2 \text{sexmale} +\beta_3 \text{(height*sexmale)}+ \epsilon \\ \end{aligned} \]

于是，可以将上面的公式里男性(sexmale = 1)和女性(sexmale = 0)分别表示

\[ \begin{aligned} \text{female}\qquad earn &= \alpha + \beta_1 \text{height} +\epsilon \\ \text{male}\qquad earn &= \alpha + \beta_1 \text{height} + \beta_2 *1 +\beta_3 \text{(height*1)}+ \epsilon \\ &= \alpha + \beta_1 \text{height} + \beta_2 +\beta_3 \text{height}+ \epsilon \\ & = (\alpha + \beta_2) + (\beta_1 + \beta_3)\text{height} + \epsilon \\ \end{aligned} \] 我们再对比mod6结果中的系数\(\alpha, \beta_1, \beta_2, \beta_3\)

mod6
## 
## Call:
## lm(formula = earn ~ height + sex + height:sex, data = wages)
## 
## Coefficients:
##    (Intercept)          height         sexmale  height:sexmale  
##       -12167.0           564.5        -30510.4           701.4

是不是更容易理解呢？

  • 对于女性，(截距\(\alpha\)，系数\(\beta_1\))，height增长1个单位，引起earn的增长564.5102
  • 对于男性，(截距\(\alpha + \beta_2\)，系数\(\beta_1 + \beta_3\))，height增长1个单位，引起earn的增长564.5102 + 701.4065 = 1265.92

事实上，对于男性和女性，截距和系数都不同，因此这种情形等价于，按照sex分成两组，男性算男性的斜率，女性算女性的斜率

wages %>%
  group_by(sex) %>%
  group_modify(
    ~ broom::tidy(lm(earn ~ height, data = .))
  )
## # A tibble: 4 × 6
## # Groups:   sex [2]
##   sex    term        estimate std.error statistic p.value
##   <chr>  <chr>          <dbl>     <dbl>     <dbl>   <dbl>
## 1 female (Intercept)  -12167.    20160.    -0.604  0.546 
## 2 female height          565.      312.     1.81   0.0710
## 3 male   (Intercept)  -42677.    38653.    -1.10   0.270 
## 4 male   height         1266.      551.     2.30   0.0221
wages %>%
  ggplot(aes(x = height, y = earn, color = sex)) +
  geom_smooth(method = lm, se = F)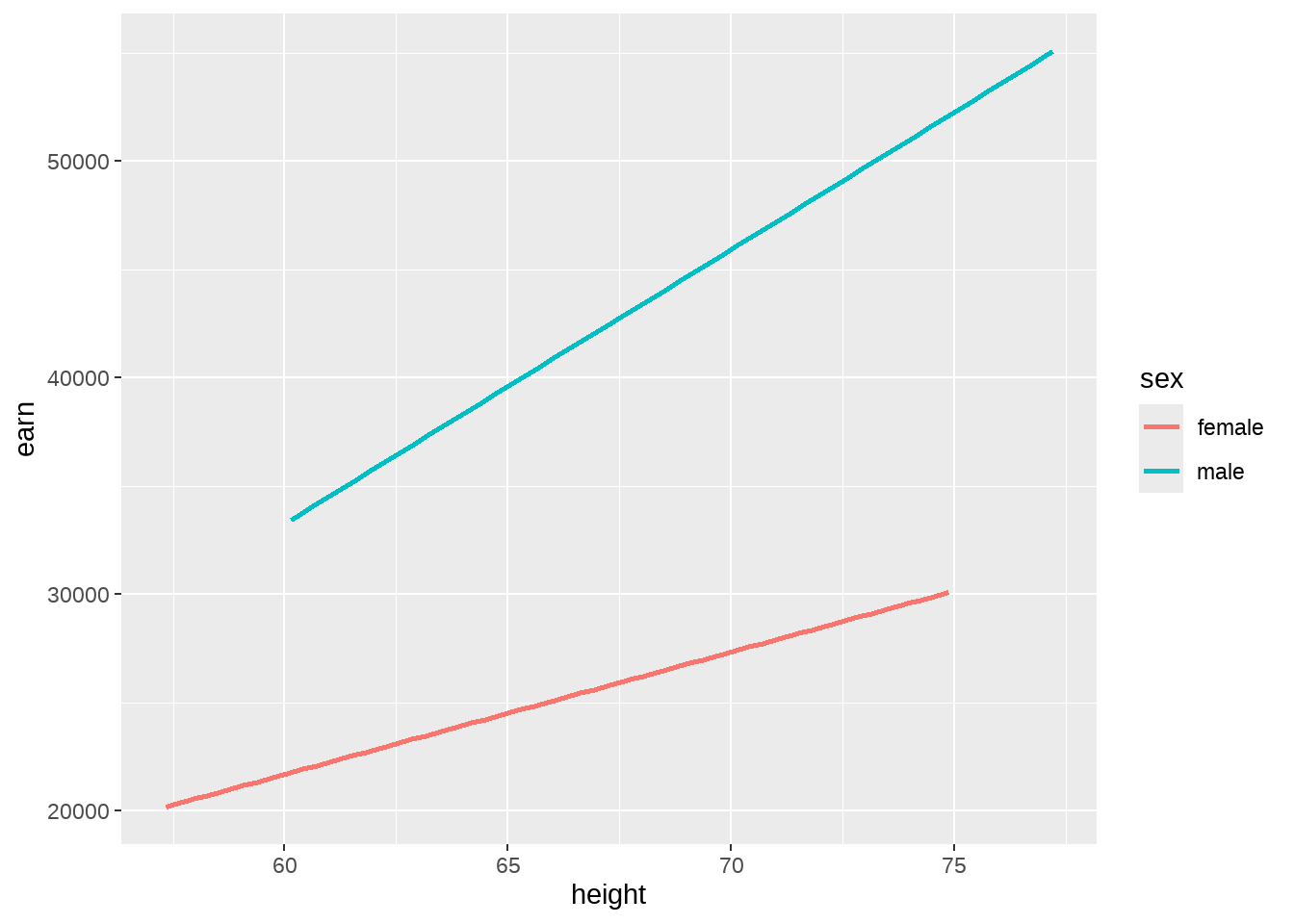
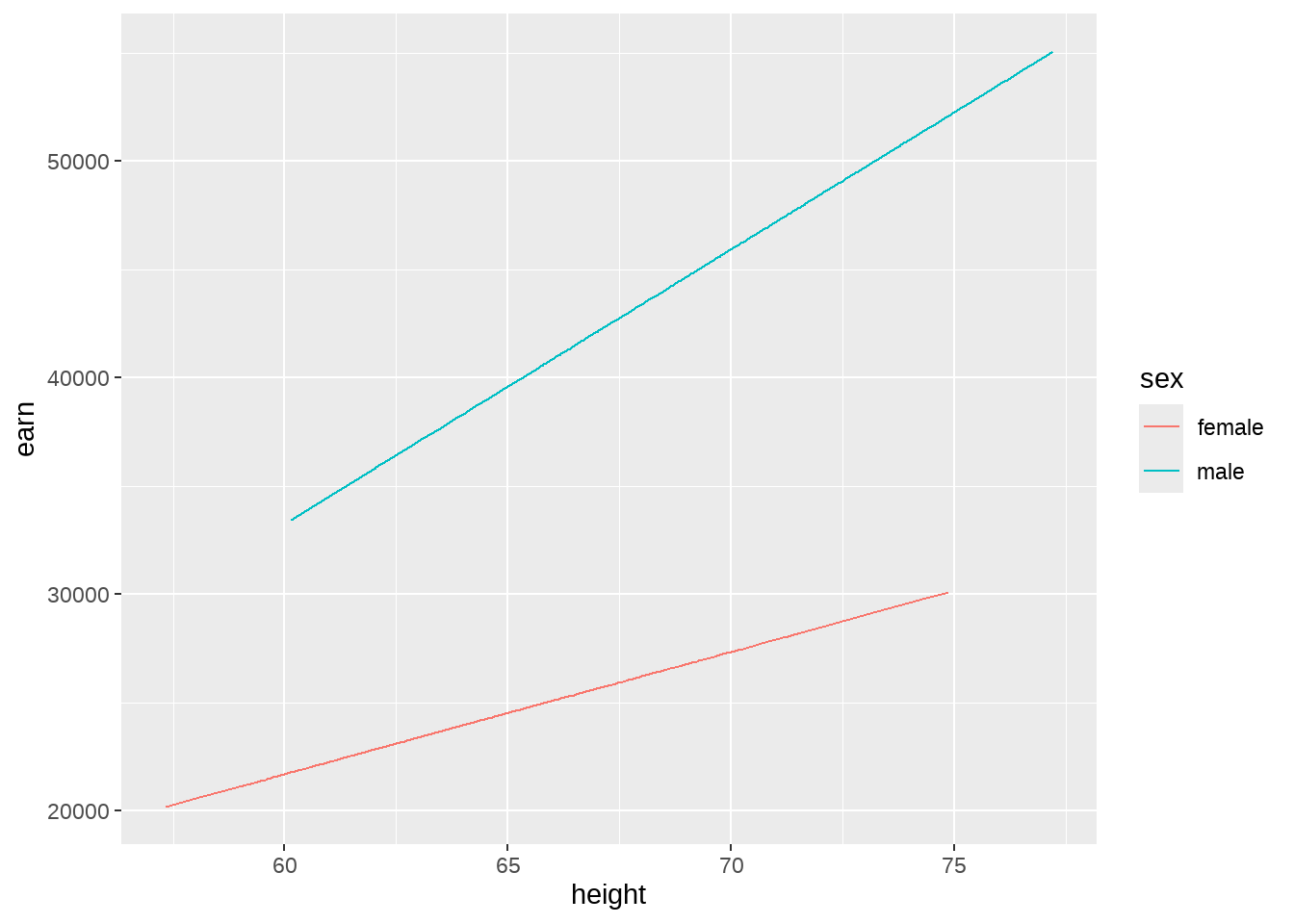
wages %>%
  ggplot(aes(x = height, y = earn, color = sex)) +
  geom_line(aes(y = predict(mod6)))

如果再特殊一点的模型（有点过分了）

mod7 <- lm(earn ~ height + height:sex, data = wages)
coef(mod7)
##    (Intercept)         height height:sexmale 
##    -24632.6695       757.4661       251.2915

这又怎么理解呢？

我们还是按照数学模型来理解，这里对应的数学表达式 \[ \begin{aligned} \text{earn} &= \alpha + \beta_1 \text{height} + \beta_4 \text{(height*sex)}+ \epsilon \\ \end{aligned} \]

引入虚拟变量

\[ \begin{aligned} \text{earn} &= \alpha + \beta_1 \text{height} + \beta_4 \text{(height*sexmale)}+ \epsilon \\ \end{aligned} \]

同样假定男性(sexmale = 1)和女性(sexmale = 0)，那么 \[ \begin{aligned} \text{female}\qquad earn &= \alpha + \beta_1 \text{height} +\epsilon \\ \text{male}\qquad earn &= \alpha + \beta_1 \text{height} + \beta_4 \text{(height*1)}+ \epsilon \\ &= \alpha + \beta_1 \text{height} + \beta_4 \text{height}+ \epsilon \\ & = \alpha + (\beta_1 + \beta_4)\text{height} + \epsilon \\ \end{aligned} \]

对照模型mod7的结果，我们可以理解：

  • 对于女性(截距\(\alpha\)，系数\(\beta_1\))，height增长1个单位，引起earn的增长757.4661
  • 对于男性(截距\(\alpha\)，系数$_1 + _4 $)，height增长1个单位，引起earn的增长757.4661 + 251.2915 = 1008.758
  • 注意到，mod6和mod7是两个不同的模型,
    • mod7中男女拟合曲线在y轴的截距是相同的，而mod6在y轴的截距是不同的

51.8.9 predict vs fit

  • fitted() , 模型一旦建立，可以使用拟合函数fitted()返回拟合值，建模和拟合使用的是同一数据
  • predict()， 模型建立后，可以用新的数据进行预测，predict()要求数据框包含新的预测变量，如果没有提供，那么就使用建模时的预测变量进行预测，这种情况下，得出的结果和fitted()就时一回事了。

predict()函数和fitted()函数不同的地方，还在于predict()函数往往带有返回何种类型的选项，可以是具体数值，也可以是分类变量。具体会在第 63 章介绍。

51.8.10 回归和相关的关系

  • 相关，比如求两个变量的相关系数cor(x, y)
  • 回归，也是探寻自变量和因变量的关系，一般用来预测

回归分析中，如果自变量只有一个\(x\)，也就是模型lm(y~x)，那么回归和相关就有关联了。

比如：计算身高和收入两者的Pearson相关系数的平方

r <- cor(wages$height, wages$earn)
print(r^2)
## [1] 0.08503071

然后看看，身高和收入的线性模型

lm(formula = earn ~ height, data = wages) %>%
  broom::glance() %>%
  pull(r.squared)
## [1] 0.08503071

相关系数的平方 和 线性模型的\(R^2\)是相等的

51.9 延伸阅读

一篇极富思考性和启发性的文章《常见统计检验的本质是线性模型》

51.10 线性模型的物理解释

图中，中间蓝色点是这些数据点的均值点，线性模型可以类比为，这里有一根通过这个均值点的刚体，而每个数据点都是一个弹簧，竖直连接到刚体，很显然越远的点，对刚体的拉力越大，越近越小，最后刚体达到平衡状态，此时刚体的状态就是线性回归的直线。

可参考Least squares as springs