Skip to main content

数据科学中的 R 语言

第 75 章 贝叶斯分析案例-新冠疫苗有效率的计算

75.1 引言

纽约时报报道说，

美国制药公司辉瑞（Pfizer）和德国生物科技公司（BioNTech）11月9日率先宣布 ，根据在数国临床试验初步结果，其研发的新冠疫苗有效率达到90%以上，星期三，完整结果显示，参加疫苗实验的44000个志愿者中，共有170人确诊感染，其中安慰剂组162人，接种疫苗组仅8人，这证明了辉瑞开发的新冠疫苗有效率高达95%。

group volunteers got_covid
placebo 22000 162
vaccinated 22000 8

新冠疫苗是有效的，且有效率高达95%。 那么，这个95%是怎么计算出来的呢？它的概率是多少以及不确定性是多少呢？ 回到这个问题，我们首先需要了解，辉瑞公司是如何定义疫苗有效率的

\[ \text{VE} = 1 - \frac{p_{t}}{p_{c}} \]

其中\(p_t\)是疫苗组(vaccinated)的感染率，\(p_c\)是安慰剂组(placebo)的感染率。

75.2 模型 

library(tidyverse)
library(tidybayes)
library(rstan)
rstan_options(auto_write = TRUE)
options(mc.cores = parallel::detectCores())

然后，我们建立如下数学模型：

\[ \begin{align} y_{c} \sim \textsf{binomial}(n_{c},p_{c}) \\ y_{t} \sim \textsf{binomial}(n_{t},p_{t}) \\ p_{c} \sim \textsf{beta}(1, 1) \\ p_{t} \sim \textsf{beta}(1, 1) \end{align} \]

通过模型可以直接计算干预效果\(\textsf{effect}\)和疫苗有效性\(VE\)

\[ \begin{align} \text{effect} = p_{t} - p_{c} \\ \text{VE} = 1 - \frac{p_{t}}{p_{c}} \end{align} \]

75.3 计算

具体Stan代码如下

stan_program <- "
data {
  int<lower=1> event_c;        // num events, control
  int<lower=1> event_t;        // num events, treatment
  int<lower=1> n_c;            // num of person trial, control
  int<lower=1> n_t;            // num of person trial, treatment
}
parameters {
  real<lower=0,upper=1> p_c;    
  real<lower=0,upper=1> p_t;    
}
model {
  event_c ~ binomial(n_c, p_c);
  event_t ~ binomial(n_t, p_t);
  p_c ~ beta(1, 1);
  p_t ~ beta(1, 1);
}
generated quantities {
  real effect   = p_t - p_c;
  real VE       = 1- p_t /p_c;
  real log_odds = log(p_t / (1- p_t)) - log(p_c / (1- p_c));
}
"


stan_data <- list(
  event_c = 162,
  event_t = 8,
  n_c     = 4.4e4 / 2,
  n_t     = 4.4e4 / 2
)

mod_vaccine <- stan(model_code = stan_program, data = stan_data)

75.4 结果

最后，我们后验概率抽样

draws <- mod_vaccine %>%
  tidybayes::spread_draws(effect, VE, log_odds)

draws %>% 
  head()
## # A tibble: 6 × 6
##   .chain .iteration .draw   effect    VE log_odds
##    <int>      <int> <int>    <dbl> <dbl>    <dbl>
## 1      1          1     1 -0.00812 0.940    -2.83
## 2      1          2     2 -0.00823 0.948    -2.96
## 3      1          3     3 -0.00780 0.969    -3.48
## 4      1          4     4 -0.00676 0.961    -3.25
## 5      1          5     5 -0.00694 0.952    -3.04
## 6      1          6     6 -0.00648 0.945    -2.90

75.4.1 干预效果

从结果中看到effect中很多负数。事实上，effect中越多的负值，即被感染的可能性越低，说明疫苗干预效果越好

mean(draws$effect < 0) %>% round(2)
## [1] 1

结果告诉我们，疫苗有明显的干预效果。比如，我们假定10000个人接受了疫苗，那么被感染的人数以及相应的可能性，如下图

draws %>%
  ggplot(aes(x = effect * 1e4)) +
  geom_density(fill = "blue", alpha = .2) +
  expand_limits(y = 0) +
  theme_minimal() +
  xlab("效应大小") +
  ggtitle("每10000个接种疫苗的人中被感染新冠的数量")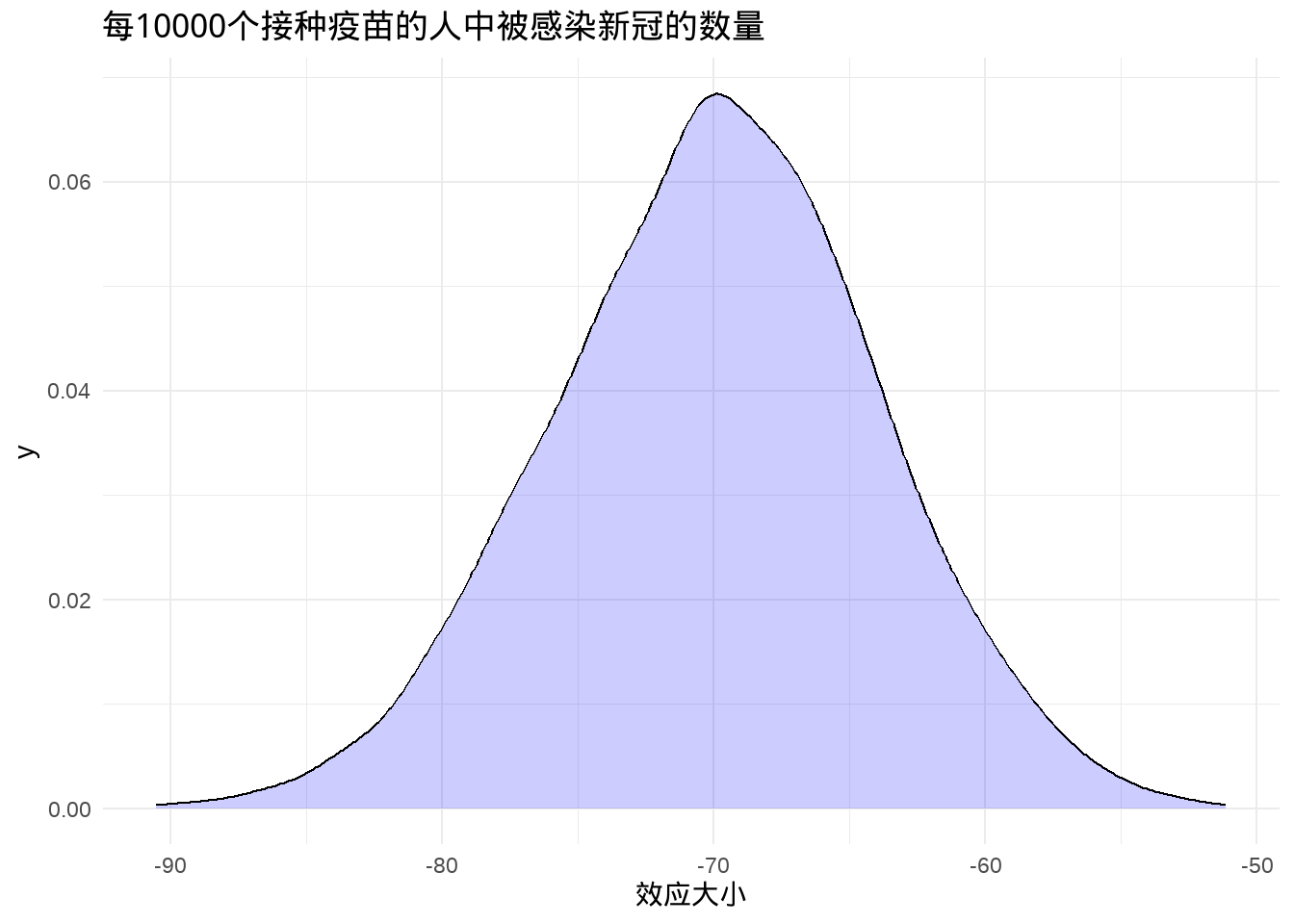

75.4.2 疫苗有效率

我们再看看疫苗有效率 VE 的结果

draws %>%
  select(VE) %>%
  ggdist::median_qi(.width = c(0.90))
## # A tibble: 1 × 6
##      VE .lower .upper .width .point .interval
##   <dbl>  <dbl>  <dbl>  <dbl> <chr>  <chr>    
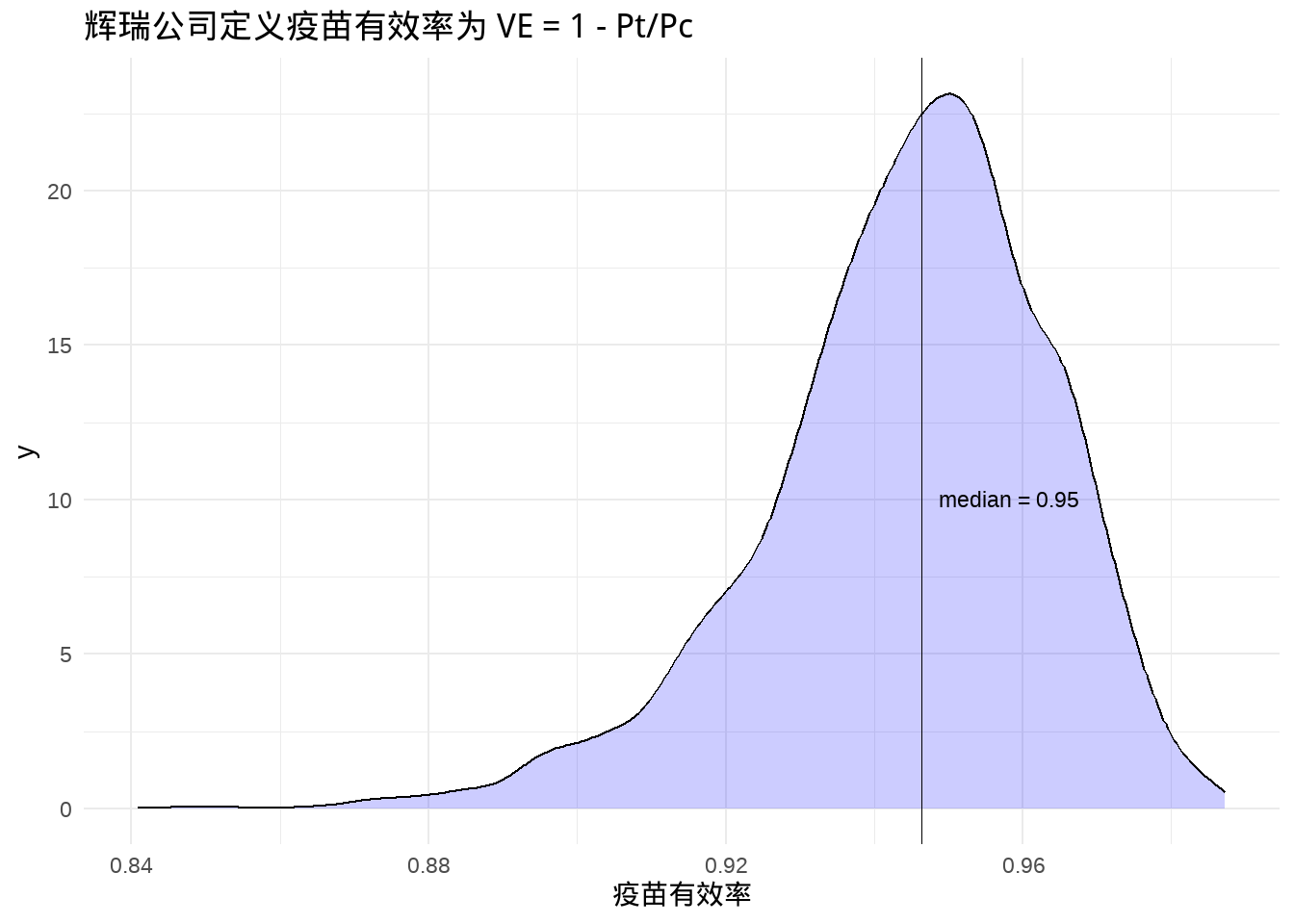
## 1 0.946  0.909  0.972    0.9 median qi

通过数据看出，疫苗的有效性为0.95，在90%的可信赖水平, 中位数区间[0.91, 0.97].

当然，通过图可能理解的更清晰。

label_txt <- paste("median =", round(median(draws$VE), 2))

draws %>%
  ggplot(aes(x = VE)) +
  geom_density(fill = "blue", alpha = .2) +
  expand_limits(y = 0) +
  theme_minimal() +
  geom_vline(xintercept = median(draws$VE), size = 0.2) +
  annotate("text", x = 0.958, y = 10, label = label_txt, size = 3) +
  xlab("疫苗有效率") +
  ggtitle("辉瑞公司定义疫苗有效率为 VE = 1 - Pt/Pc")