Skip to main content

数据科学中的 R 语言

第 64 章 贝叶斯推断

之前我们讲了线性模型和混合线性模型，今天我们往前一步，应该说是一大步。因为这一步迈向了贝叶斯分析，与频率学派的分析有本质的区别，这种区别类似经典物理和量子物理的区别。

  • 频率学派，是从数据出发
  • 贝叶斯。先假定参数有一个分布，看到数据后，再重新分配可能性。

Statistical inference is the process of using observed data to infer properties of the statistical distributions that generated that data.

简单点说

\[ \Pr(\text{parameters} | \text{data}). \]

这个量实际上贝叶斯定理中的后验概率分布(posterior distribution)

\[ \underbrace{\Pr(\text{parameters} | \text{data})}_{\text{posterior}} = \frac{\overbrace{\Pr(\text{data} | \text{parameters})}^{\text{likelihood}} \overbrace{\Pr(\text{parameters})}^{\text{prior}}}{\underbrace{\Pr(\text{data})}_{evidence}} . \]

下面，通过具体的案例演示简单的贝叶斯推断(Bayesian inference)

64.1 学生身高的分布？

假定这是收集的200位学生身高和体重数据

d <- readr::read_rds(here::here('demo_data', "height_weight.rds")) 
head(d)
##   sex   height   weight
## 1 boy 173.7173 59.93405
## 2 boy 170.8879 60.03269
## 3 boy 182.1087 62.76687
## 4 boy 176.2107 55.53530
## 5 boy 167.0802 56.64638
## 6 boy 183.1166 60.60861

用dplyr函数很容易得到样本的统计量

d %>% 
  summarise(
    across(height, list(mean = mean, median = median, max = max, min = min, sd = sd))
)
##   height_mean height_median height_max height_min height_sd
## 1    164.8933      164.1618   185.2429   142.3032  7.305997
d %>% 
  ggplot(aes(x = height)) +
  geom_density()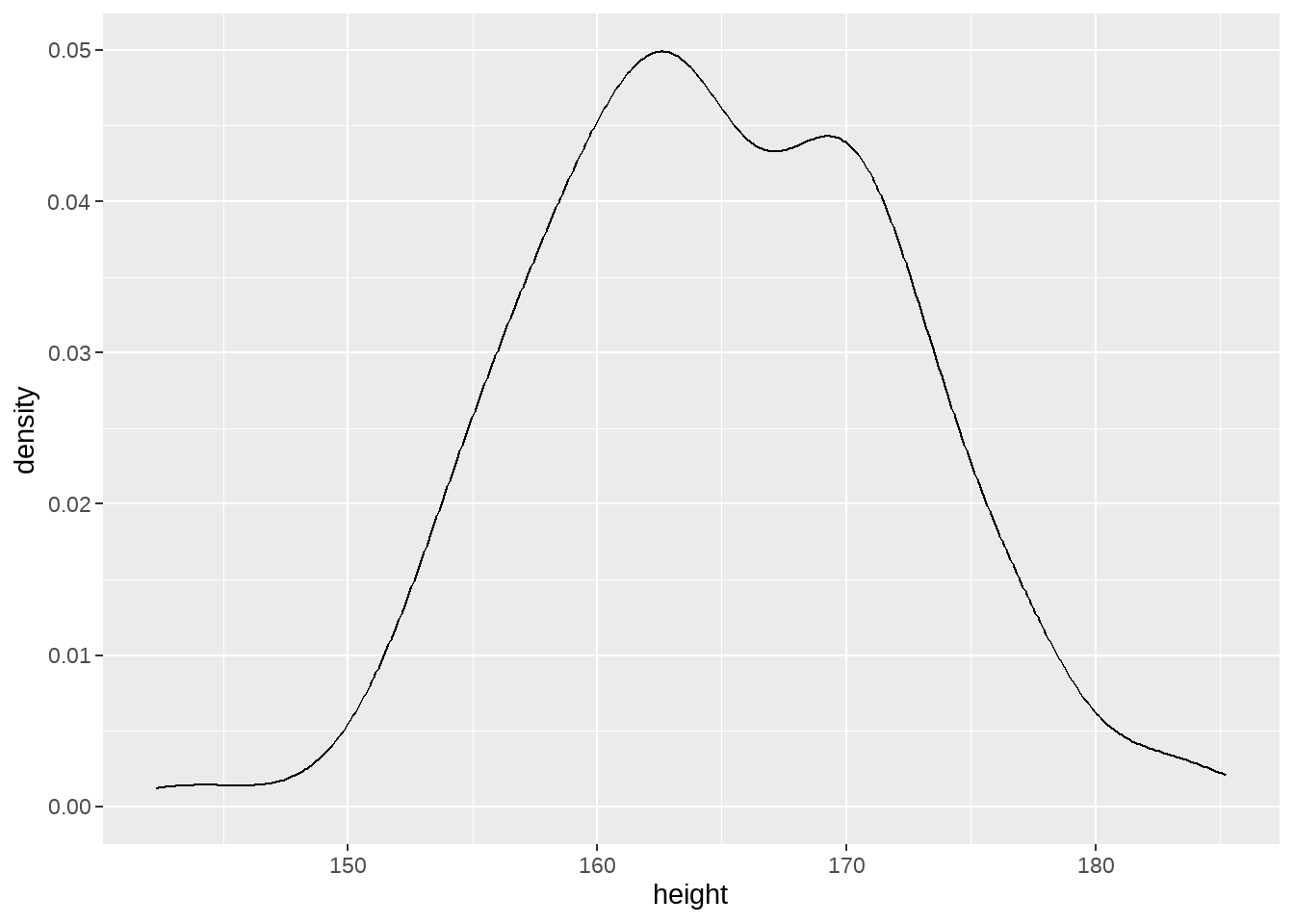

64.2 推断

注意到，我们的数据只是样本，不代表全体分布。我们只有通过样本去推断全体分布情况。

通过前面的身高的统计量，我们可以合理的猜测：

  • 均值可能是160，162，170，172，…, 或者说这个均值在一个范围之内，在这个范围内，有些值的可能性大，有些值可能性较低。比如，认为这值游离在(150,180)范围，其中168左右的可能最大，两端的可能性最低。如果寻求用数学语言来描述，它符合正态分布的特征

  • 方差也可以假设在(0, 50)范围内都有可能，而且每个位置上的概率都相等

把我们的猜测画出来就是这样的，

library(patchwork)
p1 <- 
  ggplot(data = tibble(x = seq(from = 100, to = 230, by = .1)), 
       aes(x = x, y = dnorm(x, mean = 168, sd = 20))) +
  geom_line() +
  xlab("height_mean") +
  ylab("density")


p2 <- 
  ggplot(data = tibble(x = seq(from = -10, to = 55, by = .1)), 
       aes(x = x, y =  dunif(x, min  = 0,   max = 50))) +
  geom_line() +
  xlab("height_sd") +
  ylab("density")

p1 + p2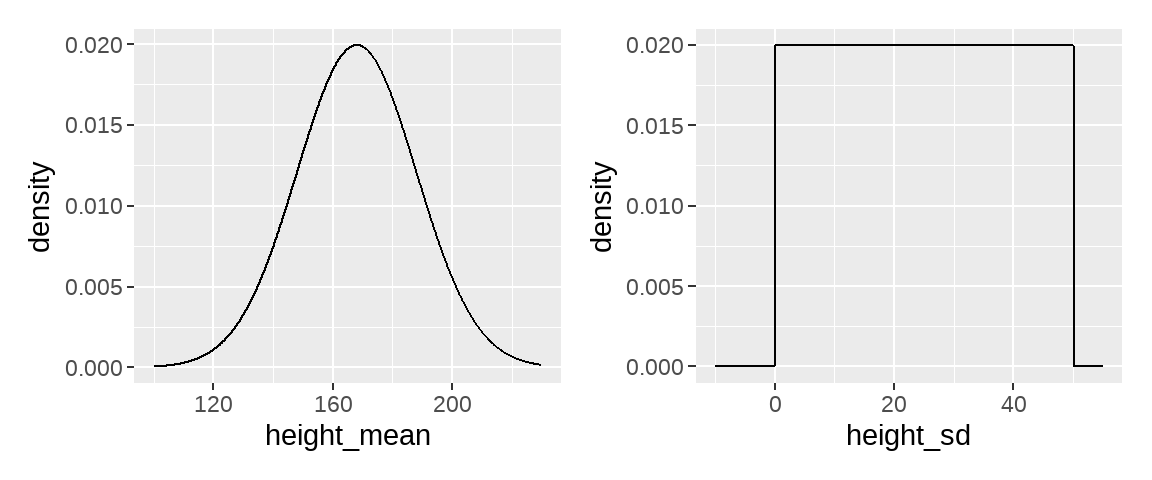

64.2.1 参数空间

我们这里构建 1000*1000个 (mu, sigma) 参数空间

d_grid <- crossing(
     mu = seq(from = 150, to = 190, length.out = 1000),
  sigma = seq(from = 4,   to = 9,   length.out = 1000)
)

d_grid
## # A tibble: 1,000,000 × 2
##       mu sigma
##    <dbl> <dbl>
##  1   150  4   
##  2   150  4.01
##  3   150  4.01
##  4   150  4.02
##  5   150  4.02
##  6   150  4.03
##  7   150  4.03
##  8   150  4.04
##  9   150  4.04
## 10   150  4.05
## # ℹ 999,990 more rows

64.2.2 likelihood

参数空间里，计算在每个(mu, sigma)组合下，身高值(d$height)出现的概率密度dnorm(d2$height, mean = mu, sd = sigma)，然后加起来。 很显然，不同的(mu, sigma)，概率密度之和是不一样的，我们这里有10001000 个(mu, sigma)组合， 所以会产生 10001000 个值

grid_function <- function(mu, sigma) {
    dnorm(d$height, mean = mu, sd = sigma, log = T) %>% 
        sum()
}
d_grid %>% 
    mutate(log_likelihood = map2_dbl(mu, sigma, grid_function))

64.2.3 prior 

d_grid %>% 
    mutate(prior_mu     = dnorm(mu,    mean = 178, sd  = 20, log = T),
         prior_sigma    = dunif(sigma, min  = 0,   max = 50, log = T))

64.2.4 posterior 

d_grid <-
    d_grid %>%
    mutate(log_likelihood = map2_dbl(mu, sigma, grid_function)) %>%
    mutate(prior_mu       = dnorm(mu,    mean = 168, sd  = 20, log = T),
           prior_sigma    = dunif(sigma, min  = 0,   max = 50, log = T)) %>%
    mutate(product        = log_likelihood + prior_mu + prior_sigma) %>%
    mutate(probability    = exp(product - max(product)))

head(d_grid)
## # A tibble: 6 × 7
##      mu sigma log_likelihood prior_mu prior_sigma product probability
##   <dbl> <dbl>          <dbl>    <dbl>       <dbl>   <dbl>       <dbl>
## 1   150  4            -2179.    -4.32       -3.91  -2188.           0
## 2   150  4.01         -2175.    -4.32       -3.91  -2183.           0
## 3   150  4.01         -2171.    -4.32       -3.91  -2179.           0
## 4   150  4.02         -2167.    -4.32       -3.91  -2175.           0
## 5   150  4.02         -2163.    -4.32       -3.91  -2171.           0
## 6   150  4.03         -2159.    -4.32       -3.91  -2167.           0
d_grid %>%
  ggplot(aes(x = mu, y = sigma, z = probability)) +
  geom_contour() +
  labs(
    x = expression(mu),
    y = expression(sigma)
  ) +
  coord_cartesian(
    xlim = range(d_grid$mu),
    ylim = range(d_grid$sigma)
  ) +
  theme(panel.grid = element_blank())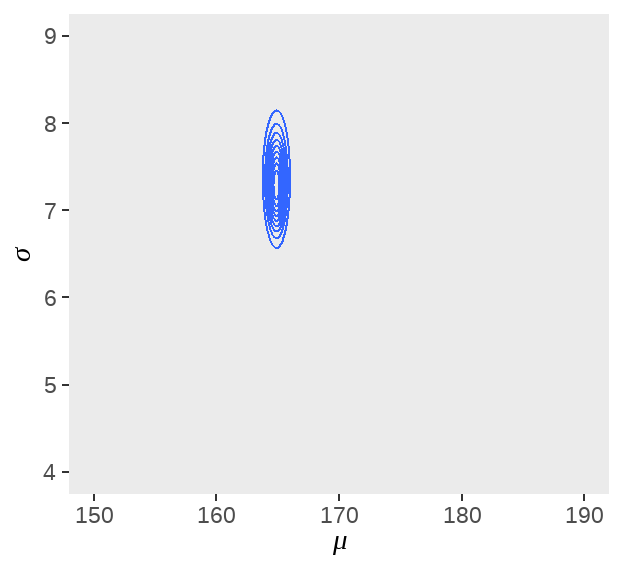
d_grid %>%
  ggplot(aes(x = mu, y = sigma)) +
  geom_raster(
    aes(fill = probability),
    interpolate = T
  ) +
  scale_fill_viridis_c(option = "A") +
  labs(
    x = expression(mu),
    y = expression(sigma)
  ) +
  theme(panel.grid = element_blank())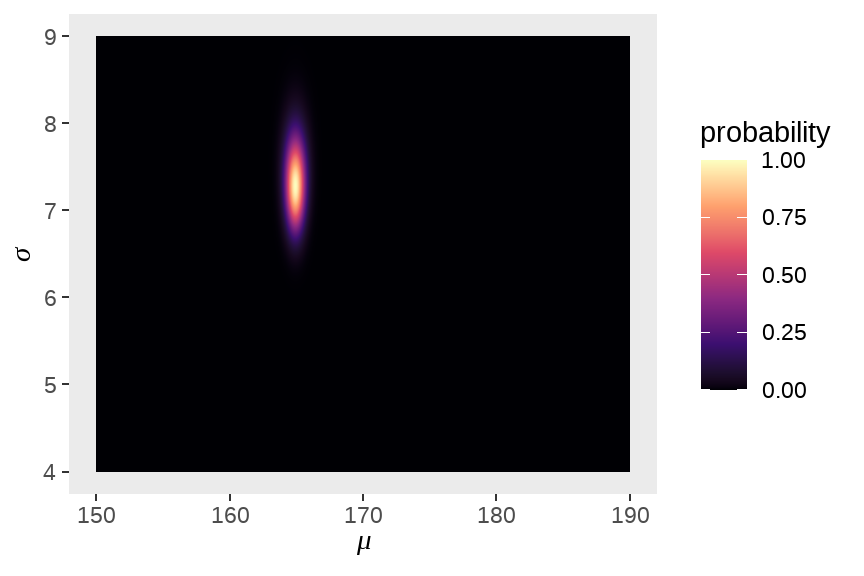

64.2.5 sampling from posterior

后验分布按照probability值的大小来抽样。

d_grid_samples <- 
    d_grid %>% 
    sample_n(size = 1e4, replace = T, weight = probability)
d_grid_samples %>% 
    ggplot(aes(x = mu, y = sigma)) + 
    geom_point(size = .9, alpha = 1/15) +
    scale_fill_viridis_c() +
    labs(x = expression(mu[samples]),
         y = expression(sigma[samples])) +
    theme(panel.grid = element_blank())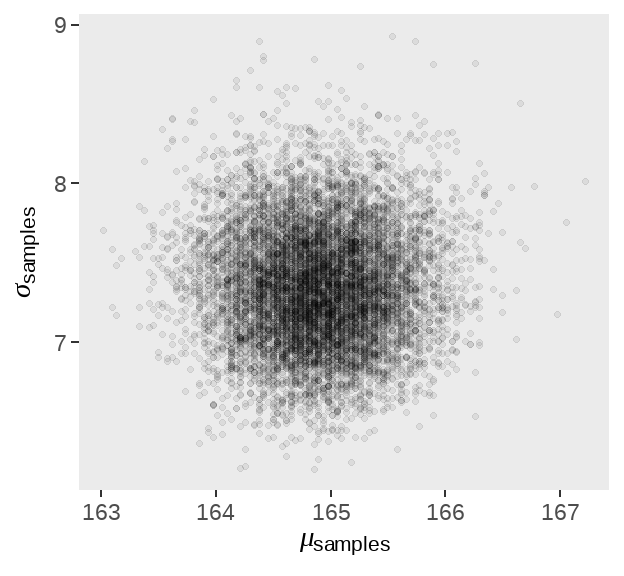
d_grid_samples %>%
    select(mu, sigma) %>%
    pivot_longer(
      cols = everything(),
      names_to = "key",
      values_to = "value"
    ) %>%
    ggplot(aes(x = value)) +
    geom_density(fill = "grey33", size = 0) +
    scale_y_continuous(NULL, breaks = NULL) +
    xlab(NULL) +
    theme(panel.grid = element_blank()) +
    facet_wrap(~key, scales = "free")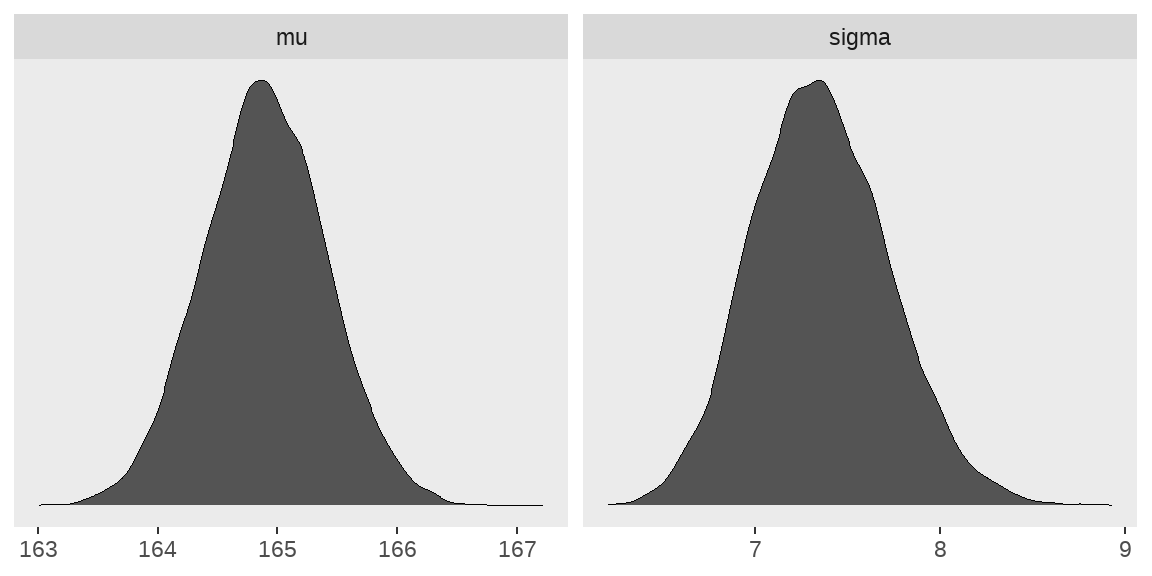

64.2.6 最高密度区间

也可以用tidybayes::mode_hdi()得到后验概率的最高密度区间

library(tidybayes)

d_grid_samples %>%
    select(mu, sigma) %>%
    pivot_longer(
      cols = everything(),
      names_to = "key",
      values_to = "value"
    ) %>%
    group_by(key) %>%
    mode_hdi(value)
## # A tibble: 2 × 7
##   key    value .lower .upper .width .point .interval
##   <chr>  <dbl>  <dbl>  <dbl>  <dbl> <chr>  <chr>    
## 1 mu    165.   164.   166.     0.95 mode   hdi      
## 2 sigma   7.33   6.62   8.05   0.95 mode   hdi

以上是通过网格近似的方法得到height分布的后验概率，但这种方法需要构建参数网格，对于较复杂的模型，计算量会陡增，内存占用大、比较费时，因此在实际的数据中，一般不采用这种方法，但网格近似的方法可以帮助我们很好地理解贝叶斯数据分析。

64.3 参考资料