第 61 章 模型的边际效应
本章介绍模型的边际效应,主要围绕marginaleffects宏包,本章的内容也是来源该宏包的说明文档。
61.1 边际效应
边际效应,测量的是某一个预测因子变化一个单位与伴随的响应变量的变化之间的关联。用数学语言表示,就是回归方程对x求偏导。
假定我们建立的回归方程是一个二次函数, \[ y = -x^2 \]
那么对x的偏导数
\[
\frac{\partial y}{\partial x} = -2x
\]
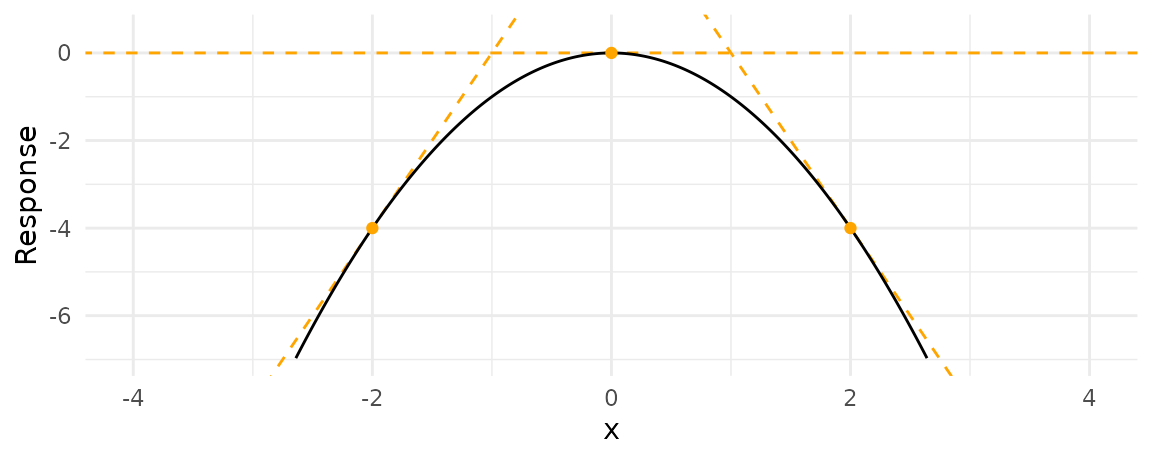
可以看到,此时的边际效应就是曲线的斜率
- 当\(x<0\),斜率为正,x增加y也增加,即,边际效应为正
- 当\(x=0\),斜率为0,在这个位置上边际效应为0
- 当\(x>0\),斜率为负,x增加y也减少,在这个位置上边际效应为负
61.2 marginaleffects function
最简单的线性模型,每个因子的边际效应就是预测因子的系数,与因子的取值无关。但是复杂点模型,因子边际效应不仅仅与因子的取值有关,而且还与其它因子的值也有关。
我们下面用企鹅数据来说明。
我们先构建一个二元变量fat_penguin(是否为胖子), 1表示是,0表示不是。并建立logitisc回归模型
dat <- penguins %>%
drop_na() %>%
mutate(
fat_penguin = if_else(body_mass_g > median(body_mass_g), 1, 0)
)
mod <- glm(
fat_penguin ~ bill_length_mm + flipper_length_mm + species,
data = dat,
family = binomial(link = "logit")
)
mod##
## Call: glm(formula = fat_penguin ~ bill_length_mm + flipper_length_mm +
## species, family = binomial(link = "logit"), data = dat)
##
## Coefficients:
## (Intercept) bill_length_mm flipper_length_mm speciesChinstrap
## -42.0591 0.3485 0.1408 -5.0386
## speciesGentoo
## 0.8165
##
## Degrees of Freedom: 332 Total (i.e. Null); 328 Residual
## Null Deviance: 461.3
## Residual Deviance: 167.3 AIC: 177.3
mfx <- marginaleffects(mod, type = "response")
head(mfx)##
## Estimate Std. Error z Pr(>|z|) S 2.5 % 97.5 %
## 0.0164 0.00807 2.04 0.04182 4.6 0.000608 0.0323
## 0.0336 0.01207 2.79 0.00534 7.5 0.009964 0.0573
## 0.0806 0.02099 3.84 < 0.001 13.0 0.039421 0.1217
## 0.0339 0.00634 5.35 < 0.001 23.4 0.021458 0.0463
## 0.0482 0.01334 3.61 < 0.001 11.7 0.022036 0.0743
## 0.0154 0.00751 2.05 0.03997 4.6 0.000707 0.0301
##
## Term: bill_length_mm
## Type: response
## Comparison: dY/dX
## Columns: rowid, term, contrast, estimate, std.error, statistic, p.value, s.value, conf.low, conf.high, predicted_lo, predicted_hi, predicted, fat_penguin, bill_length_mm, flipper_length_mm, speciesmarginaleffects() 函数对数据框dat的每一行观测给出了边际效应估计,最后输出一个数据框
。注意到,我们的模型有3个预测因子(两个连续变量,一个离散变量),一个预测因子对应一个与原数据框等长的数据框,因此最终返回的结果是原来数据框长度的3倍。
##
## Term Contrast
## bill_length_mm dY/dX
## flipper_length_mm dY/dX
## species Chinstrap - Adelie
## species Gentoo - Adelie
##
## Type: response
## Columns: term, contrast, n边际效应对连续变量非常适合。但离散变量的边际效应,不太好理解,因此采用对照方法,具体为,以某一层级为基线,那么从基线切换到其它层级,伴随着响应变量的变化,就为离散变量的边际效应。
61.3 平均边际效应
summary(mfx)## rowid term contrast estimate
## Min. : 1 Length:1332 Length:1332 Min. :-0.8509619
## 1st Qu.: 84 Class :character Class :character 1st Qu.:-0.0005831
## Median :167 Mode :character Mode :character Median : 0.0046868
## Mean :167 Mean :-0.0760268
## 3rd Qu.:250 3rd Qu.: 0.0312036
## Max. :333 Max. : 0.2013143
## std.error statistic p.value s.value
## Min. :0.0000019 Min. :-13.73671 Min. :0.0000000 Min. : 0.4411
## 1st Qu.:0.0030008 1st Qu.: 0.05123 1st Qu.:0.0002997 1st Qu.: 1.1739
## Median :0.0129358 Median : 0.76673 Median :0.0669403 Median : 3.9010
## Mean :0.0518363 Mean : 0.12734 Mean :0.2211063 Mean : 10.7010
## 3rd Qu.:0.0743682 3rd Qu.: 2.24396 3rd Qu.:0.4432341 3rd Qu.: 11.7045
## Max. :0.3190010 Max. : 8.62613 Max. :0.7365583 Max. :140.2295
## conf.low conf.high predicted_lo
## Min. :-1.1160078 Min. :-0.7194127 Min. :0.001067
## 1st Qu.:-0.2344215 1st Qu.: 0.0004169 1st Qu.:0.109107
## Median :-0.0042113 Median : 0.0149196 Median :0.594139
## Mean :-0.1776241 Mean : 0.0255705 Mean :0.550474
## 3rd Qu.: 0.0009436 3rd Qu.: 0.0643727 3rd Qu.:0.989196
## Max. : 0.0593011 Max. : 0.8136872 Max. :0.999993
## predicted_hi predicted fat_penguin bill_length_mm
## Min. :0.0000274 Min. :0.001068 Min. :0.0000 Min. :32.10
## 1st Qu.:0.0588473 1st Qu.:0.081320 1st Qu.:0.0000 1st Qu.:39.50
## Median :0.3089947 Median :0.308673 Median :0.0000 Median :44.50
## Mean :0.4650635 Mean :0.483484 Mean :0.4835 Mean :43.99
## 3rd Qu.:0.9848814 3rd Qu.:0.991639 3rd Qu.:1.0000 3rd Qu.:48.60
## Max. :0.9999933 Max. :0.999993 Max. :1.0000 Max. :59.60
## flipper_length_mm species
## Min. :172 Adelie :584
## 1st Qu.:190 Chinstrap:272
## Median :197 Gentoo :476
## Mean :201
## 3rd Qu.:213
## Max. :231