第 54 章 Tidy Statistics
一个事实是,用统计的,往往不是学统计的。
对非统计专业的初学者(比如我)感觉 t-test, ANOVAs, Chi-Square test等太不友好了,每次用的时候,我都要去翻书看我用对了没有,还要担心p-value是否徘徊在0.05附近。或许,从t-test等统计检验方法开始学统计是个错误的开始。我有时候在想,我们是不是应该更关心模型的理解,或者模型背后的理论呢。(如果和我的想法一样,就跳过本章吧)
想归想,但同学们对这方面的需求很大,所以还是打算介绍基本的方差分析内容。
54.1 方法的区分
比较几组数据之间是否有显著性差异,最常用的方法有以下几种
| X变量类型 | X组别数量 | Y变量类型 | 分析方法 | R语法 |
|---|---|---|---|---|
| 定类 | 2组或者多组 | 定量 | 方差 | aov() |
| 定类 | 仅仅2组 | 定量 | t检验 | t.test() |
| 定类 | 2组或者多组 | 定类 | 卡方 | chisq.test() |
根据X变量的个数,方差分析又分为单因素方差分析和多因素方差分析,当X的个数(不是组别数量)为1个时,我们称之为单因素方差;X的个数为2个时,则为双因素方差。
54.2 从一个案例开始
从这是一份1994年收集1379个对象关于收入、身高、教育水平等信息的数据集,数据在课件首页下载。
首先,我们下载后导入数据
| earn | height | sex | race | ed | age |
|---|---|---|---|---|---|
| 79571.30 | 73.89 | male | white | 16 | 49 |
| 96396.99 | 66.23 | female | white | 16 | 62 |
| 48710.67 | 63.77 | female | white | 16 | 33 |
| 80478.10 | 63.22 | female | other | 16 | 95 |
| 82089.35 | 63.08 | female | white | 17 | 43 |
| 15313.35 | 64.53 | female | white | 15 | 30 |
我们的问题:男性是否就比女性挣的多?
54.3 单因素方差分析
t.test(earn ~ sex, data = wages)##
## Welch Two Sample t-test
##
## data: earn by sex
## t = -11.936, df = 768.12, p-value < 2.2e-16
## alternative hypothesis: true difference in means between group female and group male is not equal to 0
## 95 percent confidence interval:
## -25324.21 -18170.74
## sample estimates:
## mean in group female mean in group male
## 24245.65 45993.13##
## Call:
## lm(formula = earn ~ sex, data = wages)
##
## Residuals:
## Min 1Q Median 3Q Max
## -46092 -20516 -4639 11722 271956
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 24246 1004 24.14 <2e-16 ***
## sexmale 21748 1636 13.30 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 29440 on 1377 degrees of freedom
## Multiple R-squared: 0.1138, Adjusted R-squared: 0.1131
## F-statistic: 176.8 on 1 and 1377 DF, p-value: < 2.2e-16## Df Sum Sq Mean Sq F value Pr(>F)
## sex 1 1.532e+11 1.532e+11 176.8 <2e-16 ***
## Residuals 1377 1.193e+12 8.665e+08
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 154.4 双因素方差分析
我们采用ggpubr宏包下的ToothGrowth来说明,这个数据集包含60个样本,记录着每10只豚鼠在不同的喂食方法和不同的药物剂量下,牙齿的生长情况.
- len : 牙齿长度
- supp : 两种喂食方法 (橙汁和维生素C)
- dose : 抗坏血酸剂量 (0.5, 1, and 2 mg)
library(ggpubr)
my_data <- ToothGrowth %>%
mutate(
across(c(supp, dose), ~ as_factor(.x))
)
my_data %>% head()## len supp dose
## 1 4.2 VC 0.5
## 2 11.5 VC 0.5
## 3 7.3 VC 0.5
## 4 5.8 VC 0.5
## 5 6.4 VC 0.5
## 6 10.0 VC 0.5
my_data %>%
ggplot(aes(x = supp, y = len, fill = supp)) +
geom_boxplot(position = position_dodge()) +
facet_wrap(vars(dose)) +
labs(title = "Effects of VC dose and intake mode on teeth of guinea pigs")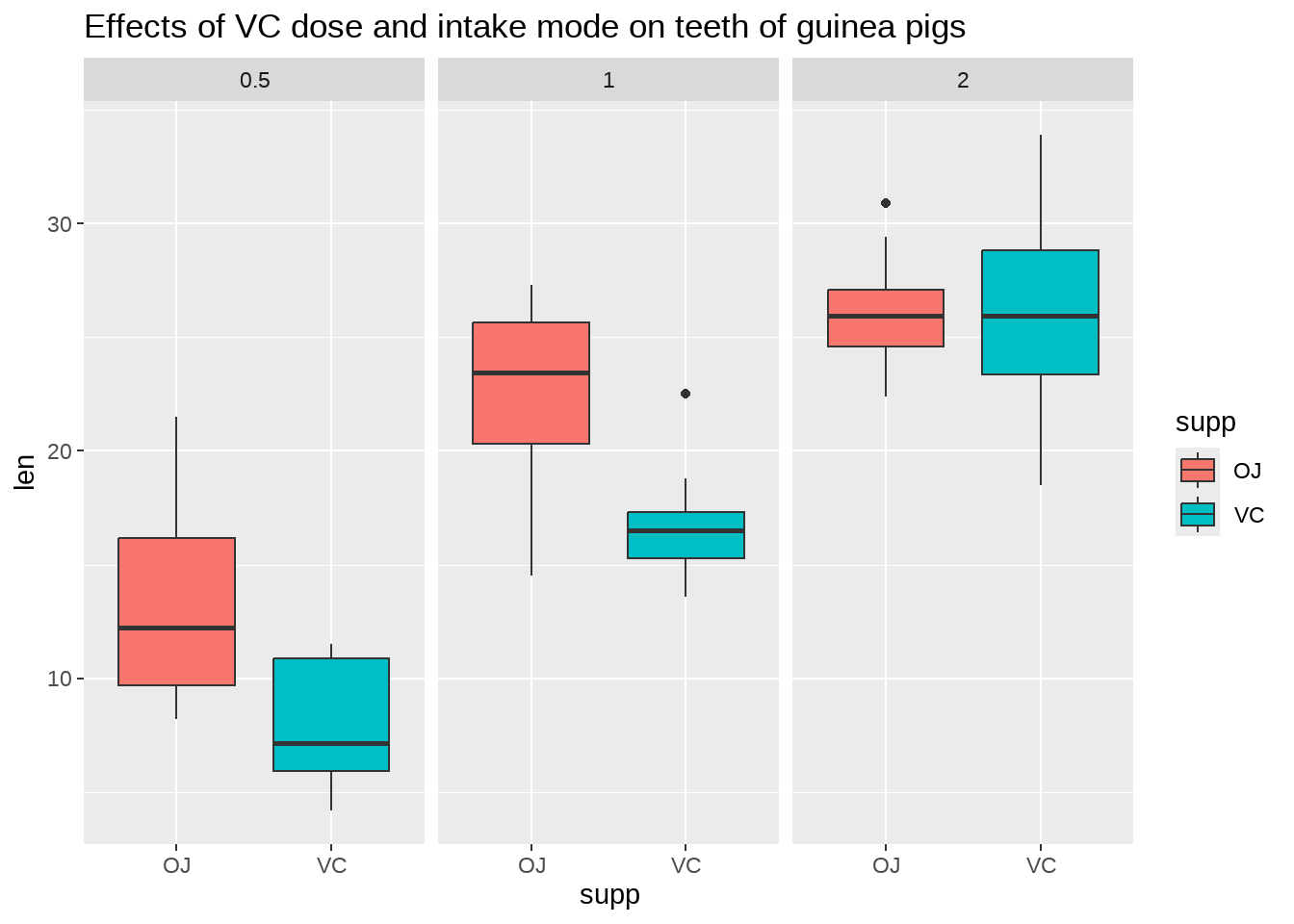
问题:豚鼠牙齿的长度是否与药物的食用方法和剂量有关?
线性回归时,我们是通过独立变量来预测响应变量,但现在我们关注的重点会从预测转向不同组别差异之间的分析,这即为方差分析(ANOVA)。
这里是两个解释变量,所以问题需要双因素方差分析 (ANOVA)
## # A tibble: 3 × 6
## term df sumsq meansq statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 supp 1 205. 205. 14.0 4.29e- 4
## 2 dose 2 2426. 1213. 82.8 1.87e-17
## 3 Residuals 56 820. 14.7 NA NA检验表明不同类型之间存在显著差异,但是并没有告诉我们具体谁与谁之间的不同。需要多重比较帮助我们解决这个问题。使用TurkeyHSD函数
## # A tibble: 3 × 7
## term contrast null.value estimate conf.low conf.high adj.p.value
## <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 dose 1-0.5 0 9.13 6.22 12.0 1.32e- 9
## 2 dose 2-0.5 0 15.5 12.6 18.4 7.31e-12
## 3 dose 2-1 0 6.37 3.45 9.28 6.98e- 6## # A tibble: 1 × 7
## term contrast null.value estimate conf.low conf.high adj.p.value
## <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 supp VC-OJ 0 -3.70 -5.68 -1.72 0.000429思考:交互效应是否显著?
## # A tibble: 4 × 6
## term df sumsq meansq statistic p.value
## <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 supp 1 205. 205. 15.6 2.31e- 4
## 2 dose 2 2426. 1213. 92.0 4.05e-18
## 3 supp:dose 2 108. 54.2 4.11 2.19e- 2
## 4 Residuals 54 712. 13.2 NA NA54.5 在tidyverse中的应用
我们也可以配合强大的tidyverse函数,完成不同分组下的方差分析,比如
mtcars %>%
group_by(cyl) %>%
summarise(
broom::tidy(aov(mpg ~ gear, data = cur_data())),
.groups = "keep"
) %>%
select(term, statistic, p.value) %>%
filter(term != "Residuals") %>%
arrange(p.value)## # A tibble: 3 × 4
## # Groups: cyl [3]
## cyl term statistic p.value
## <dbl> <chr> <dbl> <dbl>
## 1 4 gear 1.17 0.308
## 2 8 gear 0.0297 0.866
## 3 6 gear 0.000451 0.984更多使用可参考第 39 章。
54.6 使用rstatix包
rstatix包吸收了tidyverse的设计哲学,
让熟悉dplyr语法的用户能更方便的完成t-test, Wilcoxon test, ANOVA, Kruskal-Wallis等基础统计检验,
同时也增强了代码的可读性,在实际应用中还是挺受用户欢迎的,比如这本书。下面,就ToothGrowth数据,列举rstatix包的一些用法。
## # A tibble: 3 × 8
## dose .y. group1 group2 n statistic df p
## * <fct> <chr> <chr> <chr> <int> <dbl> <dbl> <dbl>
## 1 0.5 len 1 null model 20 10.5 19 2.24e- 9
## 2 1 len 1 null model 20 20.0 19 3.22e-14
## 3 2 len 1 null model 20 30.9 19 1.03e-17
# T-test
stat.test <- my_data %>%
t_test(len ~ supp, paired = FALSE)
# Create a box plot
p <- ggboxplot(
my_data, x = "supp", y = "len",
color = "supp", palette = "jco", ylim = c(0,40)
)
# Add the p-value manually
p +
stat_pvalue_manual(stat.test, label = "p", y.position = 35) +
stat_pvalue_manual(stat.test, label = "T-test, p = {p}",
y.position = 36)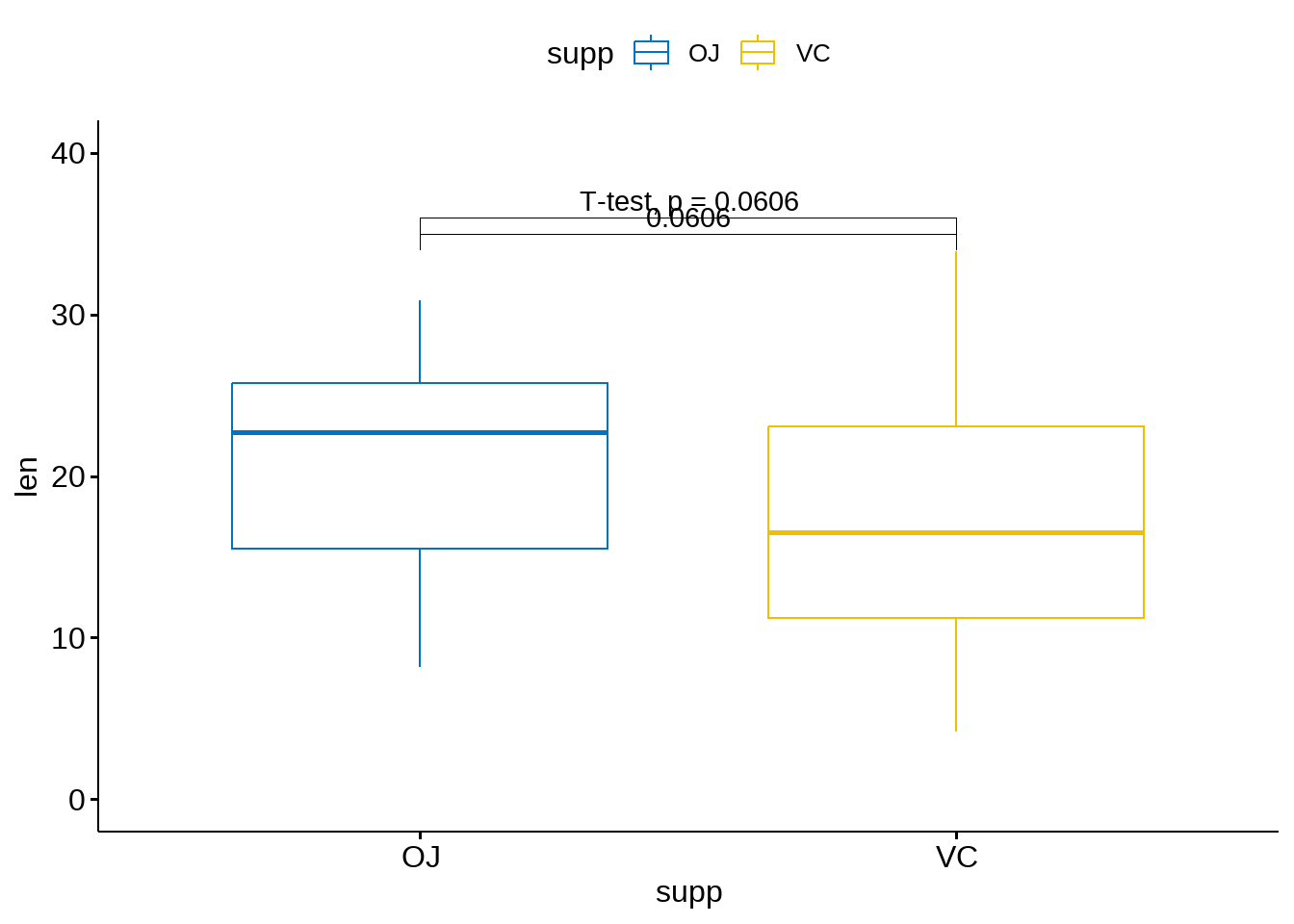
# One-way ANOVA test
my_data %>%
anova_test(len ~ dose)## ANOVA Table (type II tests)
##
## Effect DFn DFd F p p<.05 ges
## 1 dose 2 57 67.416 9.53e-16 * 0.703
# Two-way ANOVA test
my_data %>%
anova_test(len ~ supp*dose)## ANOVA Table (type II tests)
##
## Effect DFn DFd F p p<.05 ges
## 1 supp 1 54 15.572 2.31e-04 * 0.224
## 2 dose 2 54 92.000 4.05e-18 * 0.773
## 3 supp:dose 2 54 4.107 2.20e-02 * 0.132
# Two-way repeated measures ANOVA
my_data %>%
mutate(id = rep(1:10, 6) ) %>% # Add individuals id
anova_test(dv = len, wid = id, within = c(supp, dose))## ANOVA Table (type III tests)
##
## $ANOVA
## Effect DFn DFd F p p<.05 ges
## 1 supp 1 9 34.866 2.28e-04 * 0.224
## 2 dose 2 18 106.470 1.06e-10 * 0.773
## 3 supp:dose 2 18 2.534 1.07e-01 0.132
##
## $`Mauchly's Test for Sphericity`
## Effect W p p<.05
## 1 dose 0.807 0.425
## 2 supp:dose 0.934 0.761
##
## $`Sphericity Corrections`
## Effect GGe DF[GG] p[GG] p[GG]<.05 HFe DF[HF] p[HF]
## 1 dose 0.838 1.68, 15.09 2.79e-09 * 1.008 2.02, 18.15 1.06e-10
## 2 supp:dose 0.938 1.88, 16.88 1.12e-01 1.176 2.35, 21.17 1.07e-01
## p[HF]<.05
## 1 *
## 2