第 77 章 广义线性混合模型
文章数据和模型来源于Solomon Kurz的课件,我在他的基础上用Stan重写了代码
library(tidyverse)
library(tidybayes)
library(rstan)
library(loo)
rstan_options(auto_write = TRUE)
options(mc.cores = parallel::detectCores())77.1 可爱的小狗狗们学习新技能
dogs <- read.delim("./demo_data/dogs.txt") %>%
rename(dog = Dog)这里将数据宽表格转换成长表格的形式
dogs <- dogs %>%
pivot_longer(-dog, values_to = "y") %>%
mutate(trial = str_remove(name, "T.") %>% as.double())
head(dogs)## # A tibble: 6 × 4
## dog name y trial
## <int> <chr> <int> <dbl>
## 1 1 T.0 0 0
## 2 1 T.1 0 1
## 3 1 T.2 1 2
## 4 1 T.3 0 3
## 5 1 T.4 1 4
## 6 1 T.5 0 577.2 数据探索
30只狗狗需要学习新技能,每只狗有25次机会学习(trial = 0:24),y变量(0 = fail, 1 = success)
这里随机选取8只狗,看它们学习进展情况
subset <- sample(1:30, size = 8)
dogs %>%
filter(dog %in% subset) %>%
ggplot(aes(x = trial, y = y)) +
geom_point() +
scale_y_continuous(breaks = 0:1) +
theme(panel.grid = element_blank()) +
facet_wrap(~ dog, ncol = 4, labeller = label_both)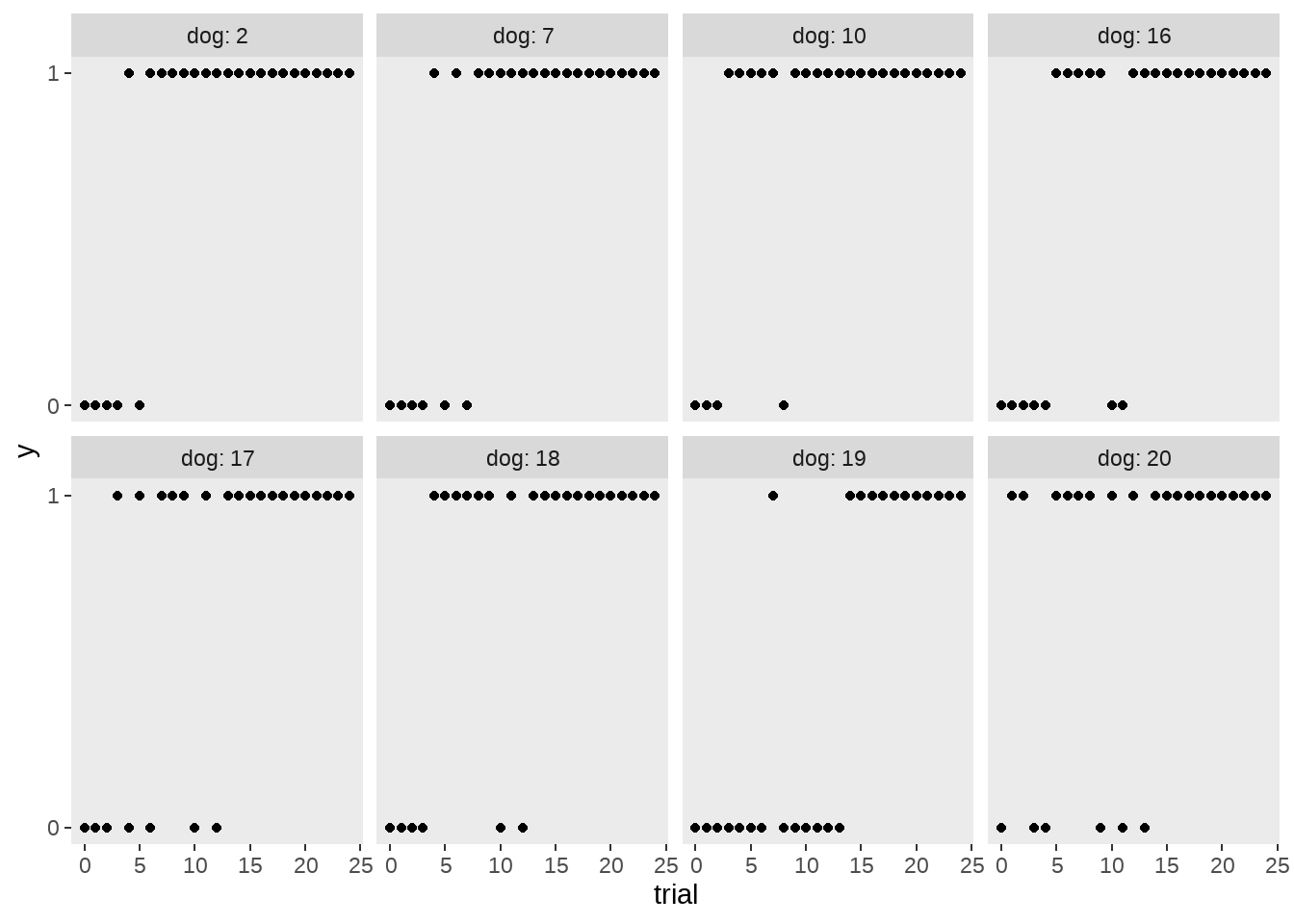
77.3 模型
由于没有更多的数据,因此我们建立最简单的logistic回归模型,并考虑多层结构(Logistic multilevel growth model)
\[ \begin{align*} \text{y}_{i} & \sim \operatorname{Binomial}(1, \; p_{i}) \\ \operatorname{logit} (p_{i}) & = a_{j[i]} + b_{j[i]} \text{trial}_{i} \\ a_j & = \alpha_0 + u_i \\ b_j & = \beta_0 + v_i \\ \begin{bmatrix} u_i \\ v_i \end{bmatrix} & \sim \operatorname{Normal} \left ( \begin{bmatrix} 0 \\ 0 \end{bmatrix}, \begin{bmatrix} \sigma_u^2 & \\ \sigma_{uv} & \sigma_v^2 \end{bmatrix} \right ). \end{align*} \]
原文中使用的是lmer4::glmer()
library(lme4)
fit1 <- glmer(
data = dogs,
family = binomial,
y ~ 1 + trial + (1 + trial | dog))
summary(fit1)这里用Stan代码重写如下
stan_program <- "
data {
int N;
int K;
matrix[N, K] X;
int<lower=0, upper=1> y[N];
int J;
int<lower=0, upper=J> g[N];
}
parameters {
array[J] vector[K] beta;
vector[K] MU;
vector<lower=0>[K] tau;
corr_matrix[K] Rho;
}
model {
// for(i in 1:N) {
// p[i] = inv_logit(X[i] * beta[g[i]]);
// }
//
// for(i in 1:N) {
// y[i] ~ bernoulli(p[i]);
// }
for(i in 1:N) {
y[i] ~ bernoulli_logit(X[i] * beta[g[i]]);
}
beta ~ multi_normal(MU, quad_form_diag(Rho, tau));
tau ~ exponential(1);
Rho ~ lkj_corr(2);
}
generated quantities {
vector[N] y_fit;
for(i in 1:N) {
y_fit[i] = inv_logit(X[i] * beta[g[i]]);
}
}
"
stan_data <- dogs %>%
tidybayes::compose_data(
N = n,
K = 2,
J = n_distinct(dog),
g = dog,
y = y,
X = model.matrix(~ 1 + trial, data = .)
)
mod0 <- stan(model_code = stan_program, data = stan_data)模型中加入预测后,更新为
stan_program <- "
data {
int N;
int K;
matrix[N, K] X;
int<lower=0, upper=1> y[N];
int J;
int<lower=0, upper=J> g[N];
int M;
matrix[M, K] X_new;
int<lower=0, upper=J> g_new[M];
}
parameters {
array[J] vector[K] beta;
vector[K] MU;
vector<lower=0>[K] tau;
corr_matrix[K] Rho;
}
model {
for(i in 1:N) {
y[i] ~ bernoulli_logit(X[i] * beta[g[i]]);
}
beta ~ multi_normal(MU, quad_form_diag(Rho, tau));
tau ~ exponential(1);
Rho ~ lkj_corr(2);
}
generated quantities {
vector[M] y_epred;
vector[M] y_fit;
vector[M] y_predict;
for(i in 1:M) {
y_epred[i] = inv_logit(X_new[i] * MU);
y_fit[i] = inv_logit(X_new[i] * beta[g_new[i]]);
y_predict[i] = bernoulli_logit_rng(X_new[i] * beta[g_new[i]]);
}
}
"
newdata <-
dogs %>%
tidyr::expand(
dog,
trial = seq(from = 0, to = 24, by = 0.25)
)
stan_data <- dogs %>%
tidybayes::compose_data(
N = n,
K = 2,
J = n_distinct(dog),
g = dog,
y = y,
X = model.matrix(~ 1 + trial, data = .),
M = nrow(newdata),
X_new = model.matrix(~ 1 + trial, data = newdata),
g_new = newdata$dog
)
mod <- stan(model_code = stan_program, data = stan_data)-
y_epred[i]: 固定效应对应的成功概率 -
y_fit[i]: 固定效应和随机效应,给出的是每只小狗的成功概率 -
y_predict[i]: 每只小狗的预测结果(0和1)
77.4 结果
77.4.1 看看每只小狗的成长曲线
fit <- mod %>%
tidybayes::gather_draws(y_fit[i]) %>%
ggdist::mean_qi(.value) # 不知道为什么ggdist::mean_hdi() 会多出几行
fit %>%
bind_cols(newdata) %>%
ggplot(aes(x = trial, y = .value, group = dog)) +
geom_line() +
theme(legend.position = "none") 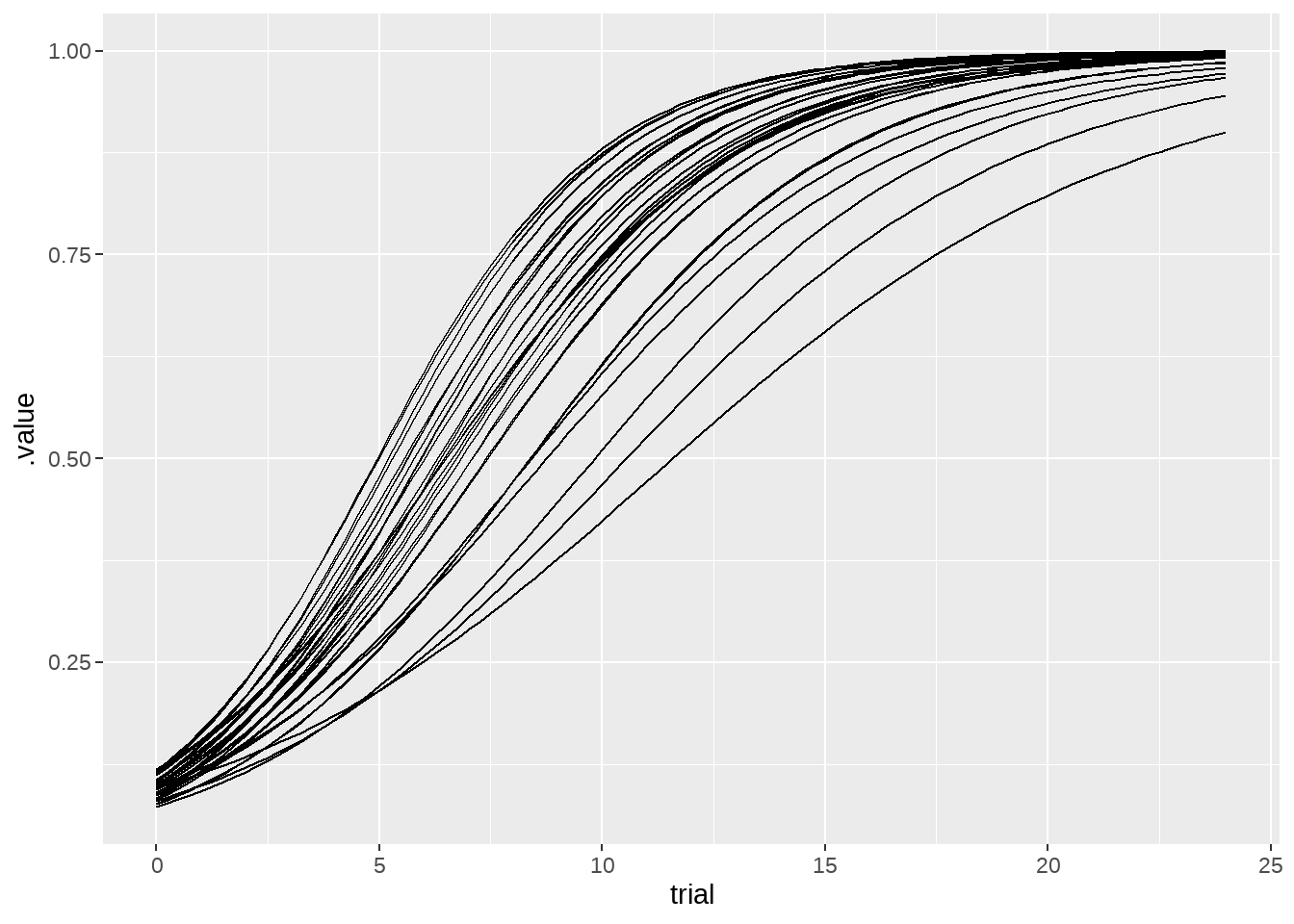
77.4.2 看看小狗们平均成长曲线
epred <- mod %>%
tidybayes::gather_draws(y_epred[i]) %>%
ggdist::mean_qi(.value)
epred %>%
bind_cols(newdata) %>%
filter(dog == 1) %>%
ggplot(aes(x = trial, y = .value, ymin = .lower, ymax = .upper)) +
geom_lineribbon() +
theme(legend.position = "none") 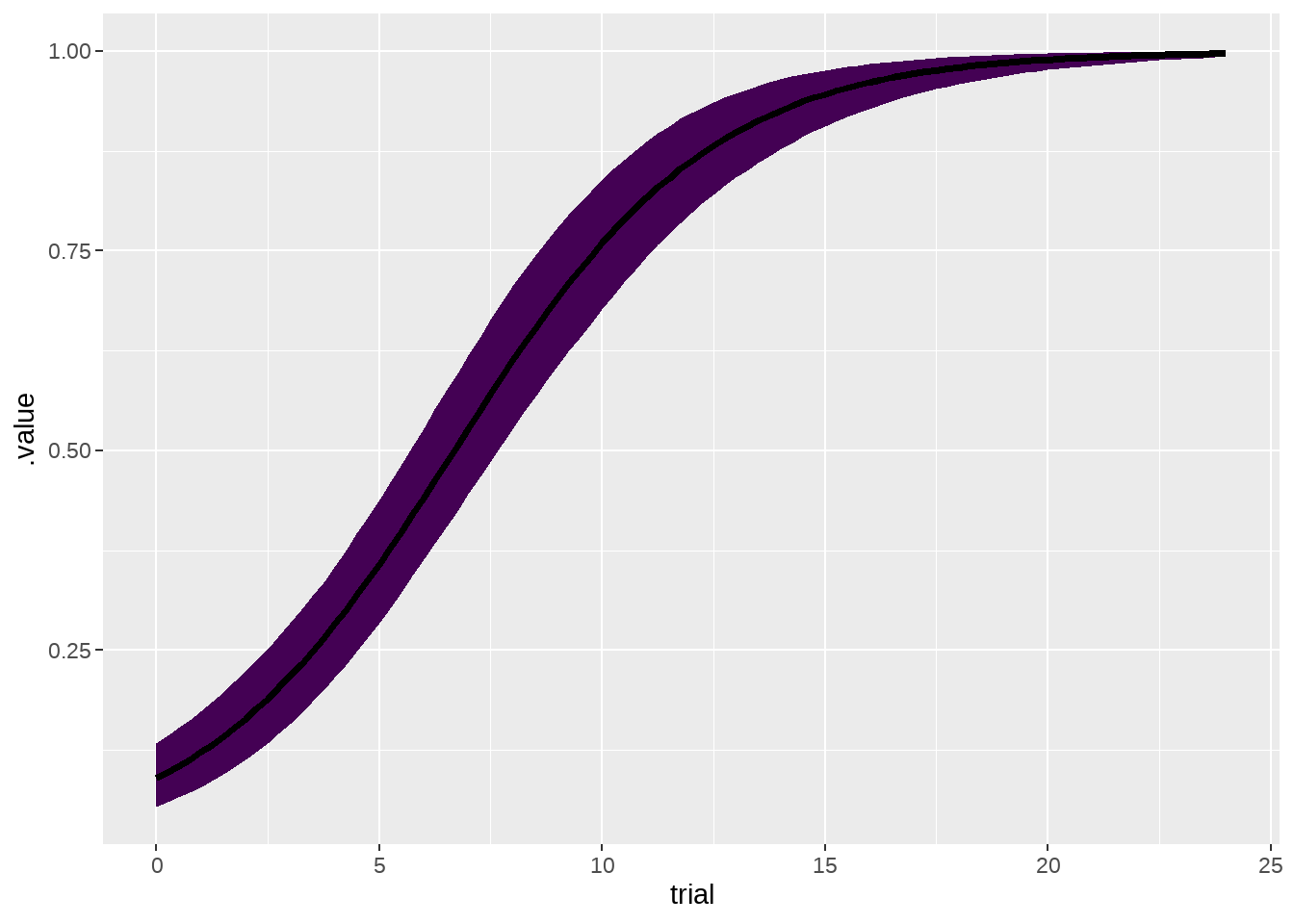
77.4.3 两张图画在一起
m <- epred %>%
bind_cols(newdata) %>%
filter(dog == 1)
fit %>%
bind_cols(newdata) %>%
ggplot(aes(x = trial, y = .value, group = dog)) +
geom_lineribbon(
data = m,
aes(ymin = .lower, ymax = .upper)
) +
geom_line() 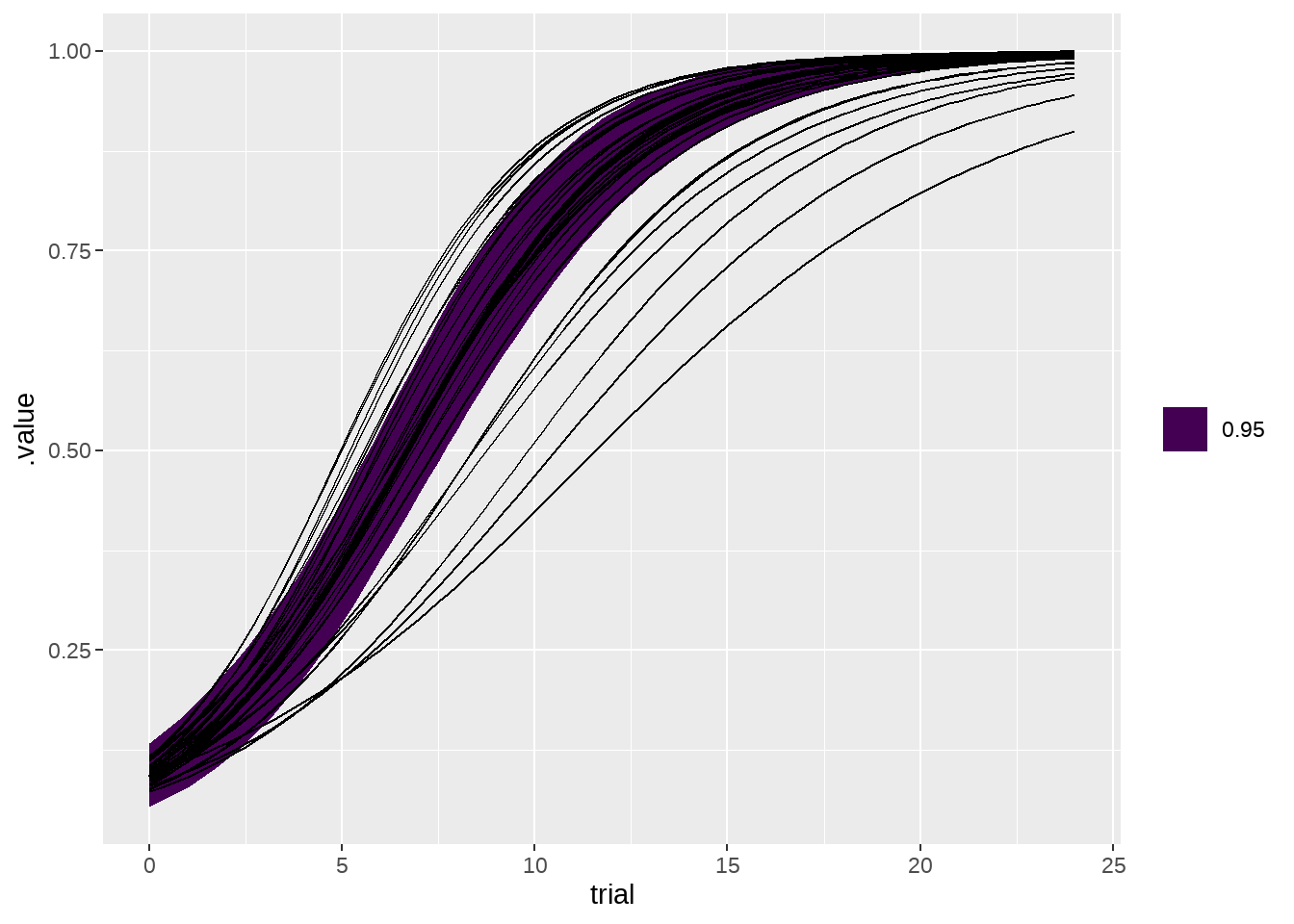
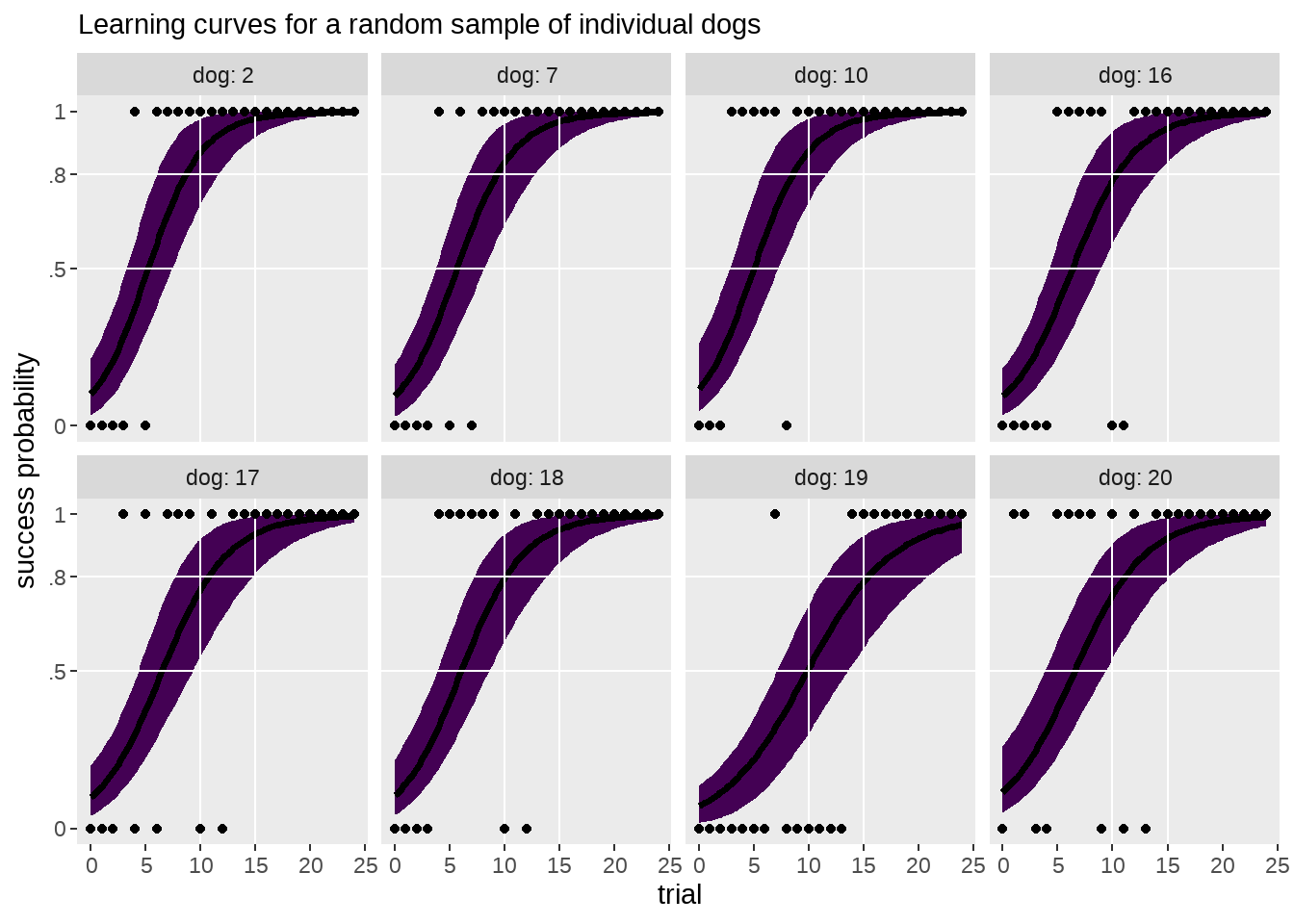
77.4.4 每只狗狗的原始数据和成长曲线画在一起
fit %>%
bind_cols(newdata) %>%
filter(dog %in% subset) %>%
ggplot(aes(x = trial, y = .value, group = dog)) +
geom_lineribbon(aes(ymin = .lower, ymax = .upper)) +
geom_vline(xintercept = 2:3 * 5, color = "white") +
geom_hline(yintercept = c(.5, .8), color = "white") +
geom_point(
data = dogs %>% filter(dog %in% subset) ,
aes(y = y)
) +
labs(
subtitle = "Learning curves for a random sample of individual dogs",
y = "success probability") +
scale_y_continuous(
breaks = c(0, .5, .8, 1), labels = c("0", ".5", ".8", "1")
) +
theme(
panel.grid.major.x = element_blank(),
panel.grid.major.y = element_blank(),
panel.grid.minor = element_blank(),
legend.position = "none"
) +
facet_wrap(~ dog, ncol = 4, labeller = label_both)