第 76 章 贝叶斯分析案例-预测奥运会男子100米短跑成绩
library(tidyverse)
library(tidybayes)
library(rstan)
library(wesanderson)
rstan_options(auto_write = TRUE)
options(mc.cores = parallel::detectCores())2020年夏季奥林匹克运动会,是第32届夏季奥林匹克运动会,于2021年7月23日至8月8日在日本东京都举行,为期17天。
76.1 男子100米短跑
以下是男子100米短跑历年冠军成绩,2012年伦敦奥运会上 Usain Bolt 跑出了9.63s的历史最好成绩。
golddata <- tibble::tribble(
~Year, ~Event, ~Athlete, ~Medal, ~Country, ~Time,
1896L, "100m Men", "Tom Burke", "GOLD", "USA", 12,
1900L, "100m Men", "Frank Jarvis", "GOLD", "USA", 11,
1904L, "100m Men", "Archie Hahn", "GOLD", "USA", 11,
1906L, "100m Men", "Archie Hahn", "GOLD", "USA", 11.2,
1908L, "100m Men", "Reggie Walker", "GOLD", "SAF", 10.8,
1912L, "100m Men", "Ralph Craig", "GOLD", "USA", 10.8,
1920L, "100m Men", "Charles Paddock", "GOLD", "USA", 10.8,
1924L, "100m Men", "Harold Abrahams", "GOLD", "GBR", 10.6,
1928L, "100m Men", "Percy Williams", "GOLD", "CAN", 10.8,
1932L, "100m Men", "Eddie Tolan", "GOLD", "USA", 10.3,
1936L, "100m Men", "Jesse Owens", "GOLD", "USA", 10.3,
1948L, "100m Men", "Harrison Dillard", "GOLD", "USA", 10.3,
1952L, "100m Men", "Lindy Remigino", "GOLD", "USA", 10.4,
1956L, "100m Men", "Bobby Morrow", "GOLD", "USA", 10.5,
1960L, "100m Men", "Armin Hary", "GOLD", "GER", 10.2,
1964L, "100m Men", "Bob Hayes", "GOLD", "USA", 10,
1968L, "100m Men", "Jim Hines", "GOLD", "USA", 9.95,
1972L, "100m Men", "Valery Borzov", "GOLD", "URS", 10.14,
1976L, "100m Men", "Hasely Crawford", "GOLD", "TRI", 10.06,
1980L, "100m Men", "Allan Wells", "GOLD", "GBR", 10.25,
1984L, "100m Men", "Carl Lewis", "GOLD", "USA", 9.99,
1988L, "100m Men", "Carl Lewis", "GOLD", "USA", 9.92,
1992L, "100m Men", "Linford Christie", "GOLD", "GBR", 9.96,
1996L, "100m Men", "Donovan Bailey", "GOLD", "CAN", 9.84,
2000L, "100m Men", "Maurice Greene", "GOLD", "USA", 9.87,
2004L, "100m Men", "Justin Gatlin", "GOLD", "USA", 9.85,
2008L, "100m Men", "Usain Bolt", "GOLD", "JAM", 9.69,
2012L, "100m Men", "Usain Bolt", "GOLD", "JAM", 9.63,
2016L, "100m Men", "Usain Bolt", "GOLD", "JAM", 9.81
)
golddata## # A tibble: 29 × 6
## Year Event Athlete Medal Country Time
## <int> <chr> <chr> <chr> <chr> <dbl>
## 1 1896 100m Men Tom Burke GOLD USA 12
## 2 1900 100m Men Frank Jarvis GOLD USA 11
## 3 1904 100m Men Archie Hahn GOLD USA 11
## 4 1906 100m Men Archie Hahn GOLD USA 11.2
## 5 1908 100m Men Reggie Walker GOLD SAF 10.8
## 6 1912 100m Men Ralph Craig GOLD USA 10.8
## 7 1920 100m Men Charles Paddock GOLD USA 10.8
## 8 1924 100m Men Harold Abrahams GOLD GBR 10.6
## 9 1928 100m Men Percy Williams GOLD CAN 10.8
## 10 1932 100m Men Eddie Tolan GOLD USA 10.3
## # ℹ 19 more rows
golddata %>%
ggplot( aes(x = Year, y = Time)) +
geom_line() +
geom_point() +
labs(title = "Winning times of Olympic gold medalist 100m sprint men")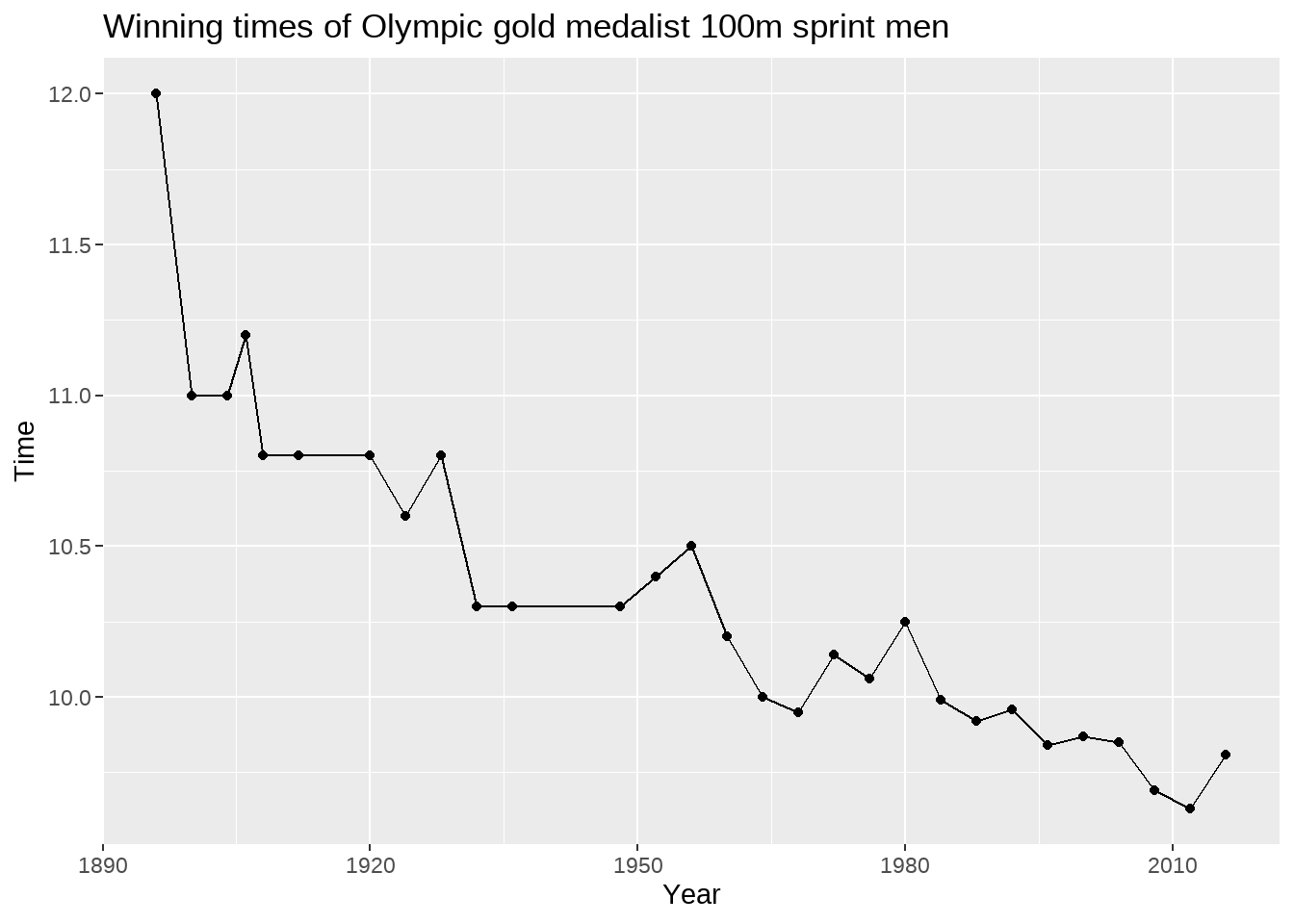
76.2 预测未来成绩
如何预测男子100米短跑未来成绩,很有挑战性。作者认为100米短跑时间符合S型曲线形状,并给出了曲线可能的数学表达式
\[ \begin{aligned} f(x) = & L + 1 - \frac{x}{\left(1 + |x|^{k}\right)^{1/k}} \\ \end{aligned} \] 当\(L=9\) 和 \(k=0.9\)时,图形是这个样子的
myfun <- function(x) {
L <- 9
k <- 0.9
L + 1 - x/((1 + abs(x)^k)^(1/k))
}
ggplot(data = data.frame(x = c(-3, 10)), aes(x = x)) +
stat_function(fun = myfun, geom = "line", colour = "red")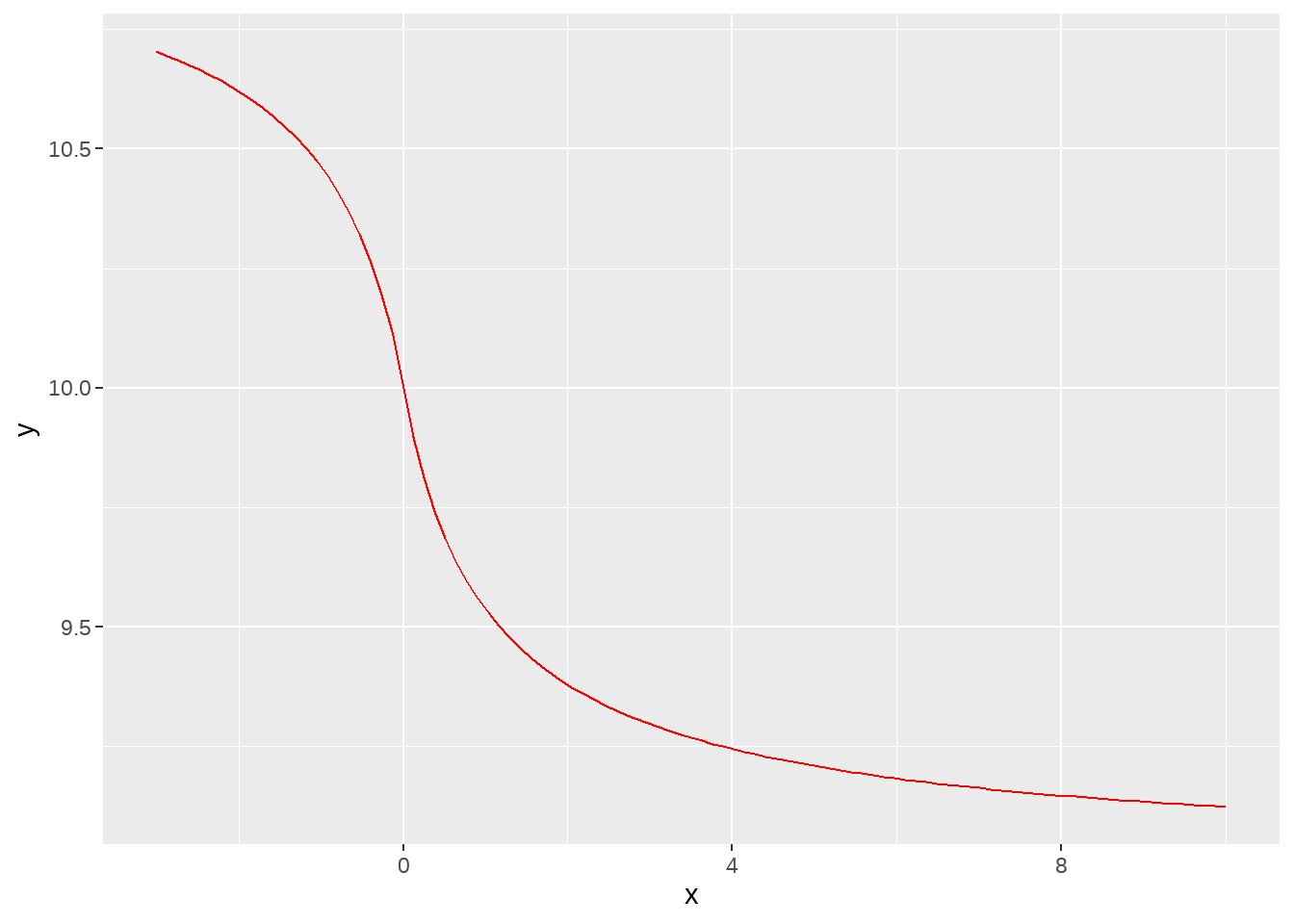
76.3 数学模型
以下,我用Stan重复了文中的贝叶斯分析过程
\[ \begin{aligned} \mathsf{Time} \sim & \mathsf{Normal}(\mu, \sigma) \\ \mu = f(\mathsf{Year}, C, S, L, k) = & L + 1 - \frac{(\mathsf{Year}-C)/S}{\left(1 + |(\mathsf{Year}-C)/S|^{k}\right)^{1/k}} \\ C\sim & \mathsf{Normal}(1959, 5) \\ S\sim & \mathsf{Normal}(37, 1) \\ L\sim & \mathsf{Normal}(9, 0.2) \\ k \sim & \mathsf{Normal}(1, 0.2)\\ \sigma \sim & \mathsf{StudentT}(3, 0, 2.5) \end{aligned} \]
首先剔除1896年的记录,因为最初的数据有点像outlier
golddata1900 <- golddata %>%
filter(Year >= 1900)
#C <- mean(golddata1900$Year)
#S <- sd(golddata1900$Year)
golddata1900## # A tibble: 28 × 6
## Year Event Athlete Medal Country Time
## <int> <chr> <chr> <chr> <chr> <dbl>
## 1 1900 100m Men Frank Jarvis GOLD USA 11
## 2 1904 100m Men Archie Hahn GOLD USA 11
## 3 1906 100m Men Archie Hahn GOLD USA 11.2
## 4 1908 100m Men Reggie Walker GOLD SAF 10.8
## 5 1912 100m Men Ralph Craig GOLD USA 10.8
## 6 1920 100m Men Charles Paddock GOLD USA 10.8
## 7 1924 100m Men Harold Abrahams GOLD GBR 10.6
## 8 1928 100m Men Percy Williams GOLD CAN 10.8
## 9 1932 100m Men Eddie Tolan GOLD USA 10.3
## 10 1936 100m Men Jesse Owens GOLD USA 10.3
## # ℹ 18 more rows76.3.1 stan code
stan_program <- "
data {
int N;
vector[N] year;
vector[N] time;
}
parameters {
real C;
real S;
real L;
real k;
real<lower=0> sigma;
}
model {
vector[N] mu;
for(i in 1:N) {
mu[i] = L + 1 - ((year[i]-C)/S) / (1+fabs((year[i]-C)/S)^k)^(1/k);
}
C ~ normal(1959, 5);
S ~ normal(37, 1);
L ~ normal(9, 0.2);
k ~ normal(1, 0.2);
sigma ~ student_t(3, 0, 2.5);
time ~ normal(mu, sigma);
}
generated quantities {
vector[N] y_rep;
for (n in 1:N) {
y_rep[n] = normal_rng(L + 1 - ((year[n]-C)/S) / (1+fabs((year[n]-C)/S)^k)^(1/k), sigma);
}
}
"
stan_data <- golddata1900 %>%
tidybayes::compose_data(
N = nrow(.),
year = Year,
time = Time
)
fit <- stan(model_code = stan_program, data = stan_data,
seed = 1024,
iter = 4000,
warmup = 2000)
bayesplot::mcmc_trace(fit, pars = c("C", "S", "L", "k", "sigma"), facet_args = list(nrow = 5))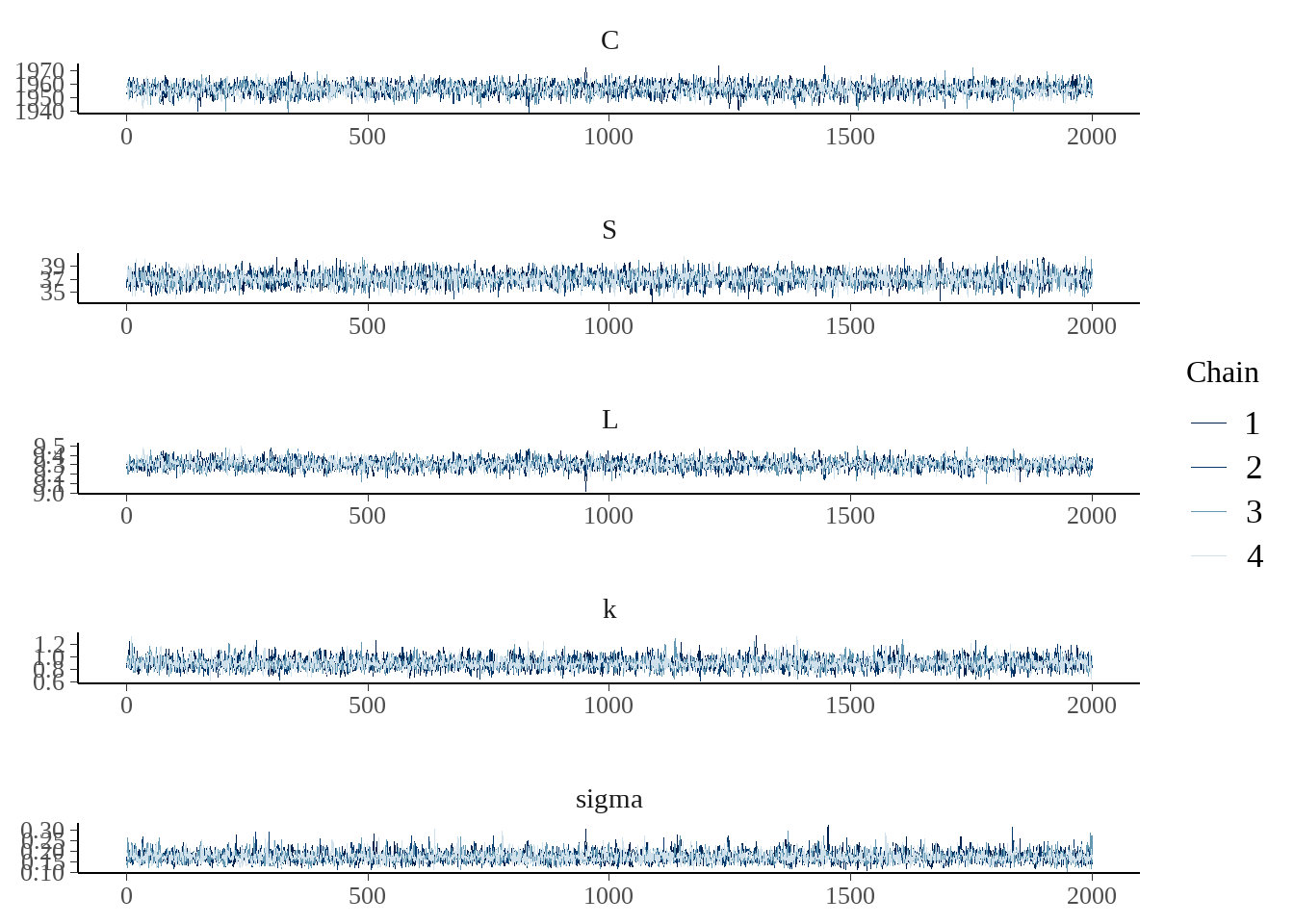
fit %>%
tidybayes::gather_draws(y_rep[i]) %>%
mean_qi() %>%
bind_cols(golddata1900) %>%
ggplot(aes(x = Year, y = Time)) +
geom_point(size = 5) +
geom_line(aes(y = .value), size = 2, color = "orange") +
geom_ribbon(aes(ymin = .lower, ymax = .upper),
alpha = 0.3,
fill = "gray50"
) +
theme_classic()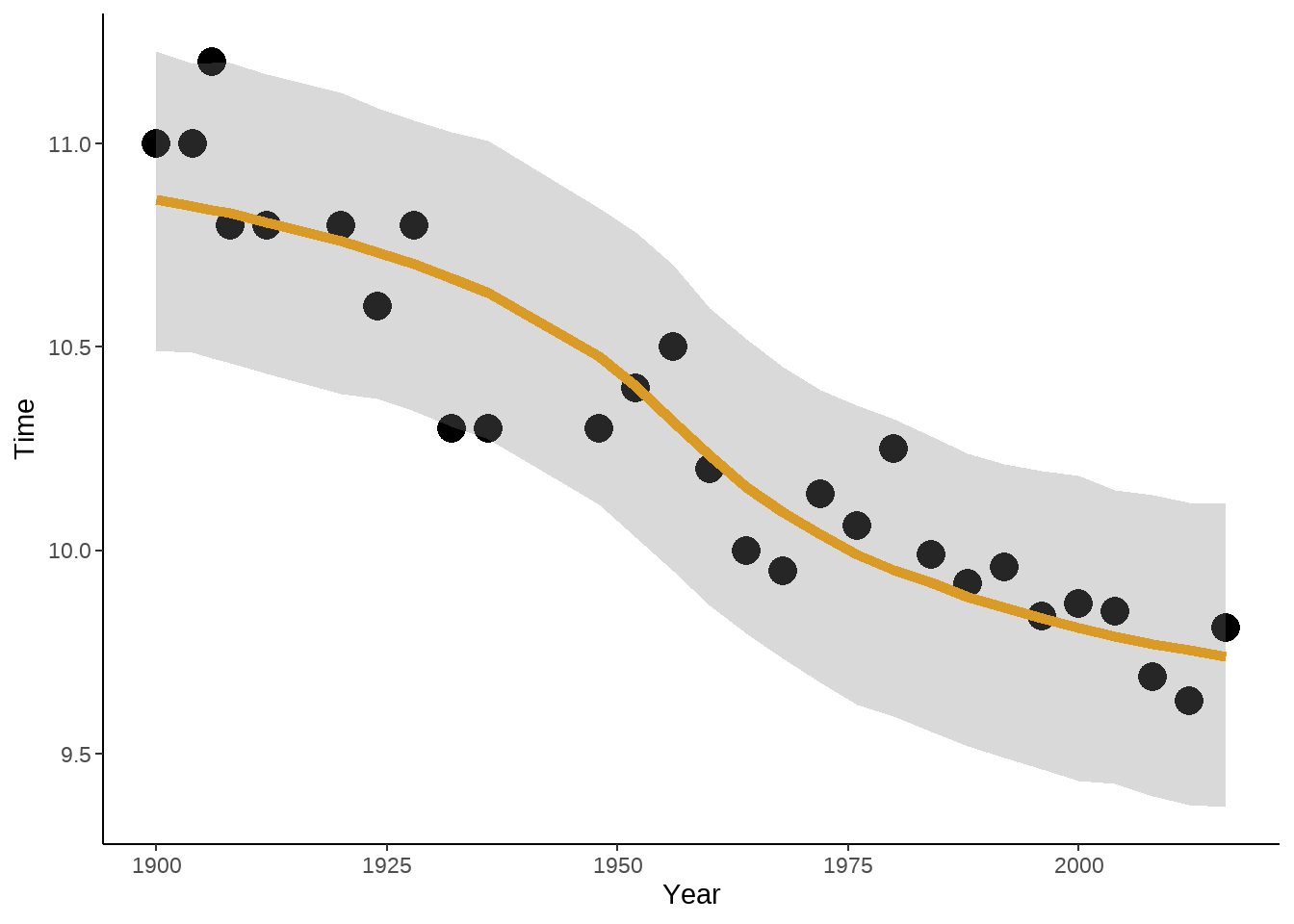
76.3.2 预测
y_pred <- function(year, C, S, L, k, sigma) {
mu <- L + 1 - ((year - C) / S) / (1 + abs((year - C) / S)^k)^(1 / k)
rnorm(n = 1, mean = mu, sd = sigma)
}
sim <- fit %>%
tidybayes::spread_draws(C, S, L, k, sigma) %>%
ungroup() %>%
rowwise() %>%
mutate(
pred2021 = y_pred(year = 2021, C, S, L, k, sigma),
pred2024 = y_pred(year = 2024, C, S, L, k, sigma),
pred2028 = y_pred(year = 2028, C, S, L, k, sigma)
) %>%
ungroup()
sim %>%
select(starts_with("pred")) %>%
map_dfr(
~tidybayes::mean_hdi(.x)
)## y ymin ymax .width .point .interval
## 1 9.720894 9.376350 10.10724 0.95 mean hdi
## 2 9.712202 9.325586 10.07234 0.95 mean hdi
## 3 9.696688 9.350349 10.07351 0.95 mean hdi76.4 方法二,直接在Stan中加入预测
具体 Stan 模型如下
stan_program <- "
data {
int N;
vector[N] year;
vector[N] time;
int M;
vector[M] new_year;
}
parameters {
real C;
real S;
real L;
real k;
real<lower=0> sigma;
}
model {
vector[N] mu;
for(i in 1:N) {
mu[i] = L + 1 - ((year[i]-C)/S) / (1+fabs((year[i]-C)/S)^k)^(1/k);
}
C ~ normal(1959, 5);
S ~ normal(37, 1);
L ~ normal(9, 0.2);
k ~ normal(1, 0.2);
sigma ~ student_t(3, 0, 2.5);
time ~ normal(mu, sigma);
}
generated quantities {
vector[N] y_rep;
vector[M] y_new;
for (n in 1:N) {
y_rep[n] = normal_rng(L + 1 - ((year[n]-C)/S) / (1+fabs((year[n]-C)/S)^k)^(1/k), sigma);
}
for (i in 1:M) {
y_new[i] = normal_rng(L + 1 - ((new_year[i]-C)/S) / (1+fabs((new_year[i]-C)/S)^k)^(1/k), sigma);
}
}
"
stan_data <- golddata1900 %>%
tidybayes::compose_data(
N = nrow(.),
year = Year,
time = Time,
M = 3,
new_year = c(2021, 2024, 2028)
)
fit2 <- stan(model_code = stan_program, data = stan_data,
seed = 1024,
iter = 4000,
warmup = 2000)
fit2 %>%
tidybayes::gather_draws(y_rep[i]) %>%
mean_qi() %>%
bind_cols(golddata1900) %>%
ggplot(aes(x = Year, y = Time)) +
geom_point(size = 5) +
geom_line(aes(y = .value), size = 2, color = "orange") +
geom_ribbon(aes(ymin = .lower, ymax = .upper),
alpha = 0.3,
fill = "gray50"
) +
theme_classic()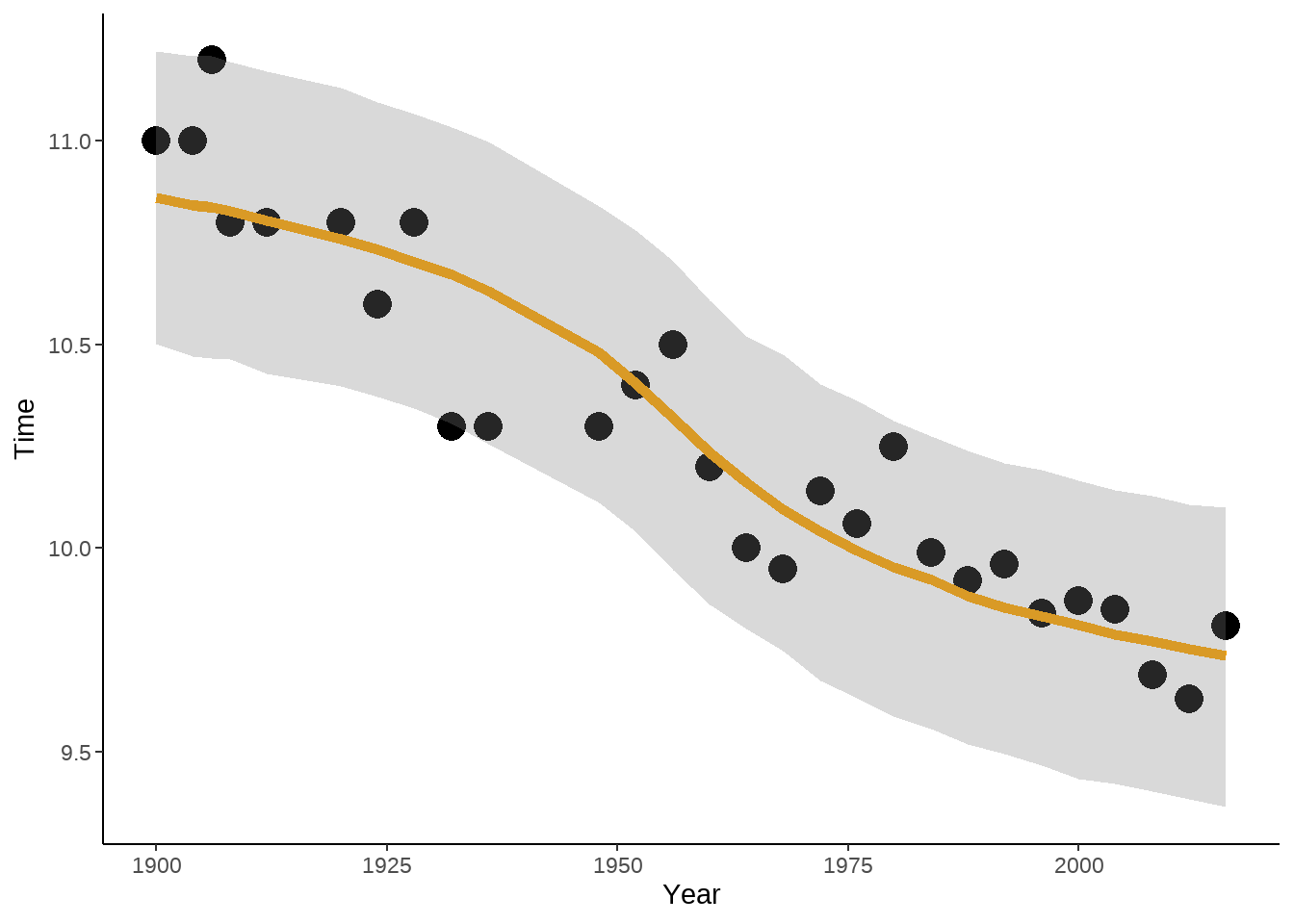
fit2 %>%
tidybayes::gather_draws(y_new[i]) %>%
mean_qi() ## # A tibble: 3 × 8
## i .variable .value .lower .upper .width .point .interval
## <int> <chr> <dbl> <dbl> <dbl> <dbl> <chr> <chr>
## 1 1 y_new 9.72 9.35 10.1 0.95 mean qi
## 2 2 y_new 9.71 9.34 10.1 0.95 mean qi
## 3 3 y_new 9.70 9.32 10.1 0.95 mean qi