第 56 章 统计推断
Statistical Inference: A Tidy Approach
56.1 案例1:你会给爱情片还是动作片高分?

这是一个关于电影评分的数据集8,
## # A tibble: 58,788 × 24
## title year length budget rating votes r1 r2 r3 r4 r5 r6
## <chr> <int> <int> <int> <dbl> <int> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 $ 1971 121 NA 6.4 348 4.5 4.5 4.5 4.5 14.5 24.5
## 2 $1000 a… 1939 71 NA 6 20 0 14.5 4.5 24.5 14.5 14.5
## 3 $21 a D… 1941 7 NA 8.2 5 0 0 0 0 0 24.5
## 4 $40,000 1996 70 NA 8.2 6 14.5 0 0 0 0 0
## 5 $50,000… 1975 71 NA 3.4 17 24.5 4.5 0 14.5 14.5 4.5
## 6 $pent 2000 91 NA 4.3 45 4.5 4.5 4.5 14.5 14.5 14.5
## 7 $windle 2002 93 NA 5.3 200 4.5 0 4.5 4.5 24.5 24.5
## 8 '15' 2002 25 NA 6.7 24 4.5 4.5 4.5 4.5 4.5 14.5
## 9 '38 1987 97 NA 6.6 18 4.5 4.5 4.5 0 0 0
## 10 '49-'17 1917 61 NA 6 51 4.5 0 4.5 4.5 4.5 44.5
## # ℹ 58,778 more rows
## # ℹ 12 more variables: r7 <dbl>, r8 <dbl>, r9 <dbl>, r10 <dbl>, mpaa <chr>,
## # Action <int>, Animation <int>, Comedy <int>, Drama <int>,
## # Documentary <int>, Romance <int>, Short <int>数据集包含58788 行 和 24 变量
| variable | description |
|---|---|
| title | 电影名 |
| year | 发行年份 |
| budget | 预算金额 |
| length | 电影时长 |
| rating | 平均得分 |
| votes | 投票人数 |
| r1-10 | 各分段投票人占比 |
| mpaa | MPAA 分级 |
| action | 动作片 |
| animation | 动画片 |
| comedy | 喜剧片 |
| drama | 戏剧 |
| documentary | 纪录片 |
| romance | 爱情片 |
| short | 短片 |
我们想看下爱情片与动作片(不是爱情动作片)的平均得分是否显著不同。
- 首先我们简单的整理下数据,主要是剔除既是爱情片又是动作片的电影
movies_genre_sample <- d %>%
select(title, year, rating, Action, Romance) %>%
filter(!(Action == 1 & Romance == 1)) %>%
mutate(genre = case_when(
Action == 1 ~ "Action",
Romance == 1 ~ "Romance",
TRUE ~ "Neither"
)) %>%
filter(genre != "Neither") %>%
select(-Action, -Romance) %>%
group_by(genre) %>%
#slice_sample(n = 34) %>% # sample size = 34
slice_head(n = 34) %>%
ungroup()
movies_genre_sample## # A tibble: 68 × 4
## title year rating genre
## <chr> <int> <dbl> <chr>
## 1 $windle 2002 5.3 Action
## 2 'A' gai waak 1983 7.1 Action
## 3 'A' gai waak juk jaap 1987 7.2 Action
## 4 'Crocodile' Dundee II 1988 5 Action
## 5 'Gator Bait 1974 3.5 Action
## 6 'Sheba, Baby' 1975 5.5 Action
## 7 ...Po prozvishchu 'Zver' 1990 4.7 Action
## 8 ...tick...tick...tick... 1970 6 Action
## 9 002 agenti segretissimi 1964 3.6 Action
## 10 10 Magnificent Killers 1977 2.6 Action
## # ℹ 58 more rows- 先看下图形
movies_genre_sample %>%
ggplot(aes(x = genre, y = rating)) +
geom_boxplot() +
geom_jitter()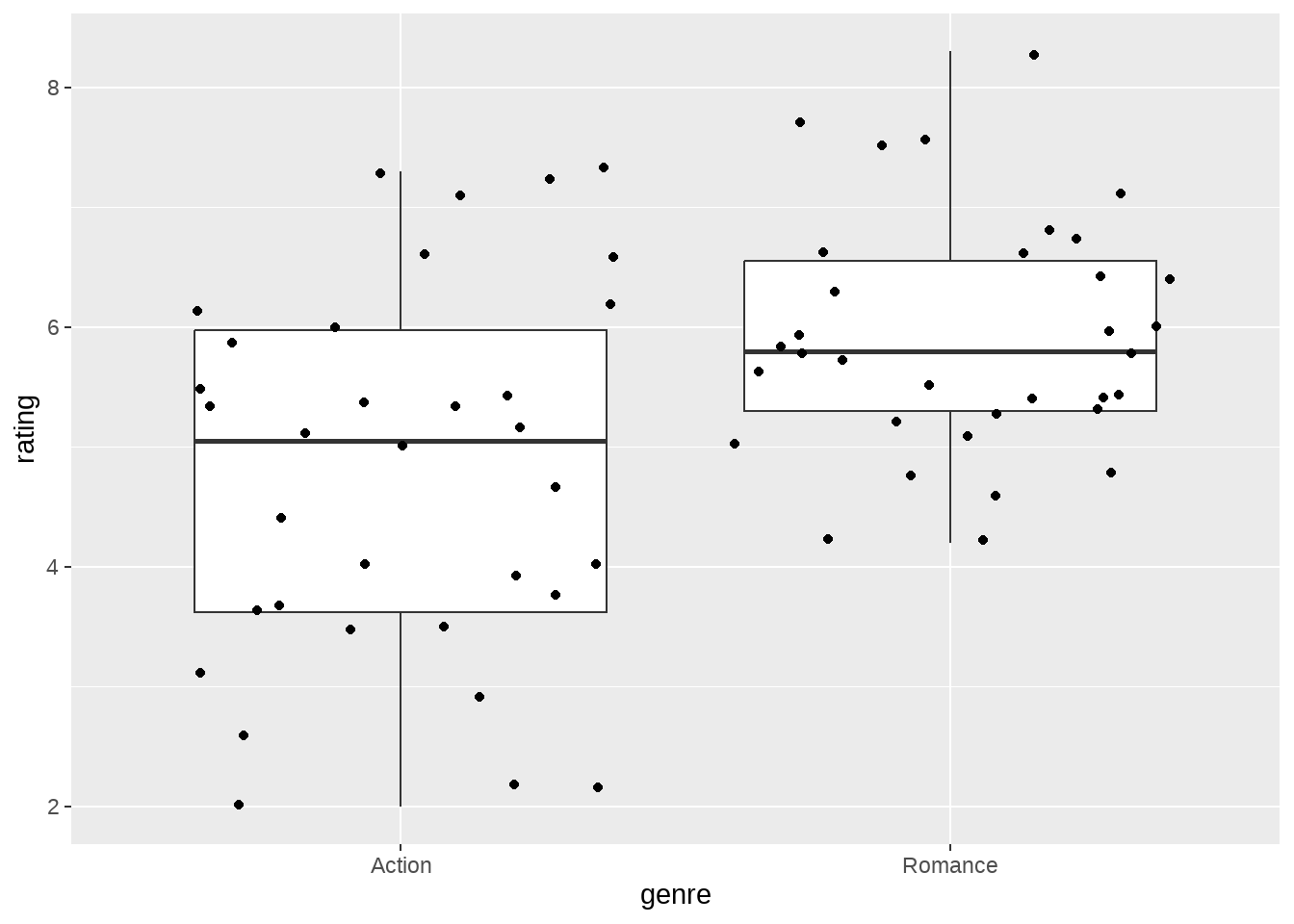
- 看下两种题材电影评分的分布
movies_genre_sample %>%
ggplot(mapping = aes(x = rating)) +
geom_histogram(binwidth = 1, color = "white") +
facet_grid(vars(genre))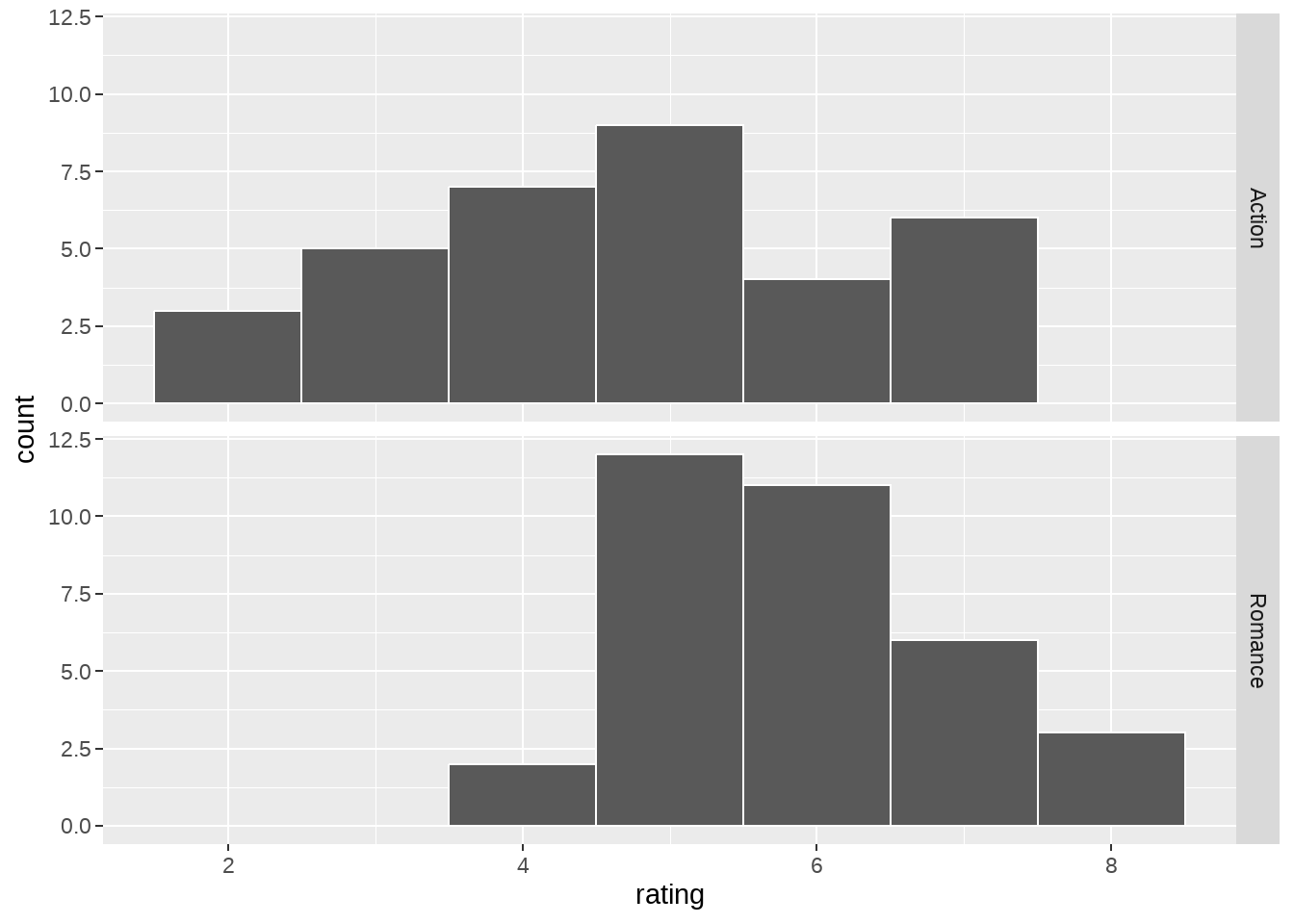
- 统计两种题材电影评分的均值
summary_ratings <- movies_genre_sample %>%
group_by(genre) %>%
summarize(
mean = mean(rating),
std_dev = sd(rating),
n = n()
)
summary_ratings## # A tibble: 2 × 4
## genre mean std_dev n
## <chr> <dbl> <dbl> <int>
## 1 Action 4.78 1.56 34
## 2 Romance 5.91 0.994 3456.1.1 传统的基于频率方法的t检验
假设:
-
零假设:
- \(H_0: \mu_{1} - \mu_{2} = 0\)
-
备选假设:
- \(H_A: \mu_{1} - \mu_{2} \neq 0\)
两种可能的结论:
- 拒绝 \(H_0\)
- 不能拒绝 \(H_0\)
t_test_eq <- t.test(rating ~ genre,
data = movies_genre_sample,
var.equal = TRUE
) %>%
broom::tidy()
t_test_eq## # A tibble: 1 × 10
## estimate estimate1 estimate2 statistic p.value parameter conf.low conf.high
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 -1.12 4.78 5.91 -3.54 0.000736 66 -1.76 -0.490
## # ℹ 2 more variables: method <chr>, alternative <chr>
t_test_uneq <- t.test(rating ~ genre,
data = movies_genre_sample,
var.equal = FALSE
) %>%
broom::tidy()
t_test_uneq## # A tibble: 1 × 10
## estimate estimate1 estimate2 statistic p.value parameter conf.low conf.high
## <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 -1.12 4.78 5.91 -3.54 0.000810 56.0 -1.76 -0.488
## # ℹ 2 more variables: method <chr>, alternative <chr>56.1.2 infer:基于模拟的检验
所有的假设检验都符合这个框架9:
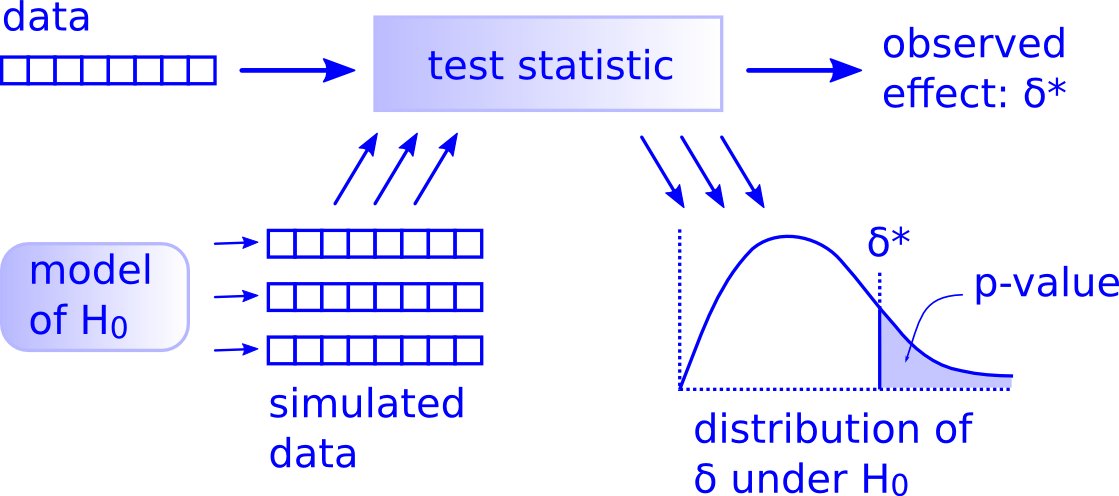
图 56.1: Hypothesis Testing Framework
- 实际观察的差别
library(infer)
obs_diff <- movies_genre_sample %>%
specify(formula = rating ~ genre) %>%
calculate(
stat = "diff in means",
order = c("Romance", "Action")
)
obs_diff## Response: rating (numeric)
## Explanatory: genre (factor)
## # A tibble: 1 × 1
## stat
## <dbl>
## 1 1.12- 模拟
null_dist <- movies_genre_sample %>%
specify(formula = rating ~ genre) %>%
hypothesize(null = "independence") %>%
generate(reps = 5000, type = "permute") %>%
calculate(
stat = "diff in means",
order = c("Romance", "Action")
)
head(null_dist)## Response: rating (numeric)
## Explanatory: genre (factor)
## Null Hypothesis: independence
## # A tibble: 6 × 2
## replicate stat
## <int> <dbl>
## 1 1 -0.194
## 2 2 -0.165
## 3 3 -0.741
## 4 4 0.141
## 5 5 0.335
## 6 6 -0.600- 可视化
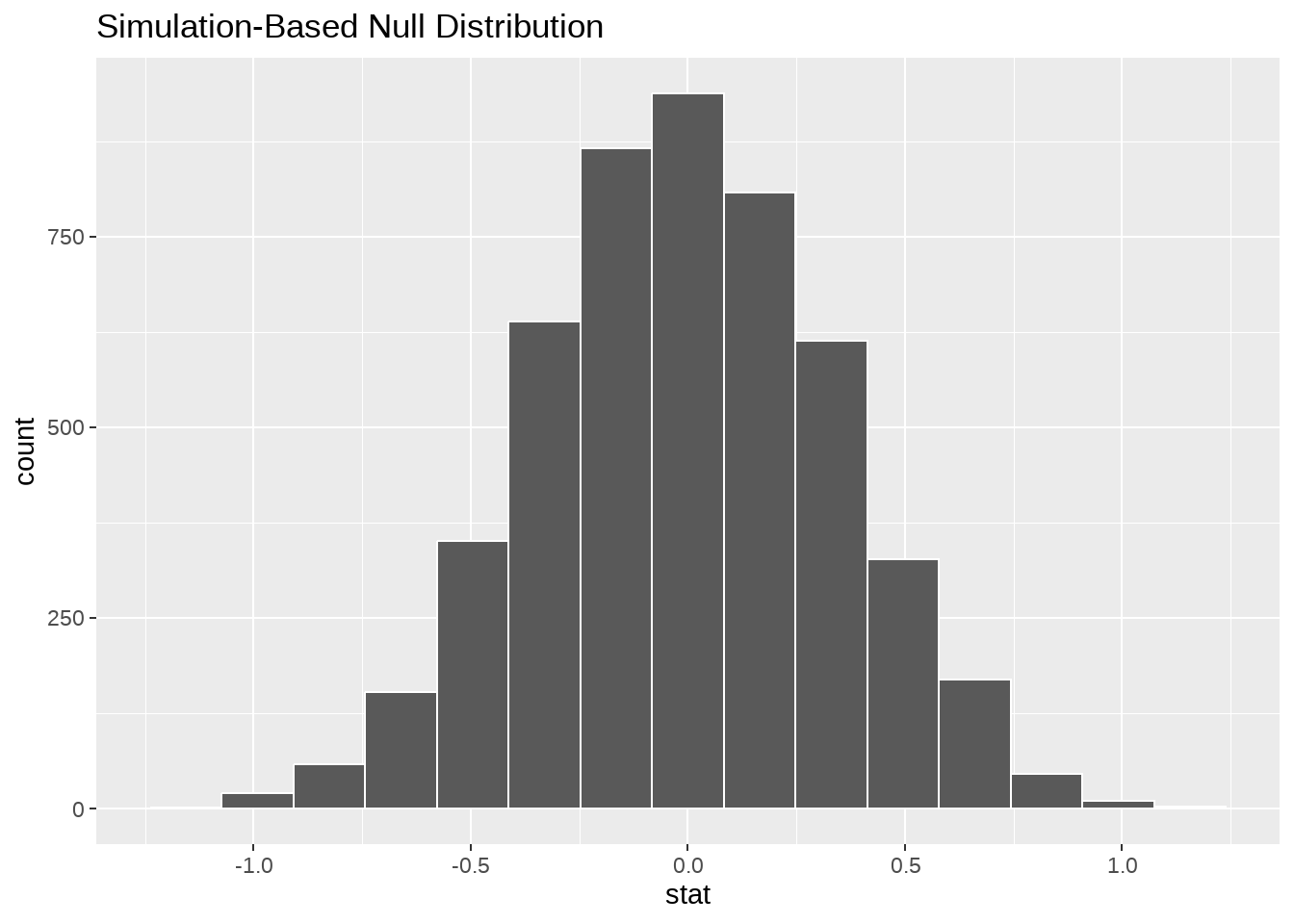
null_dist %>%
visualize() +
shade_p_value(obs_stat = obs_diff, direction = "both")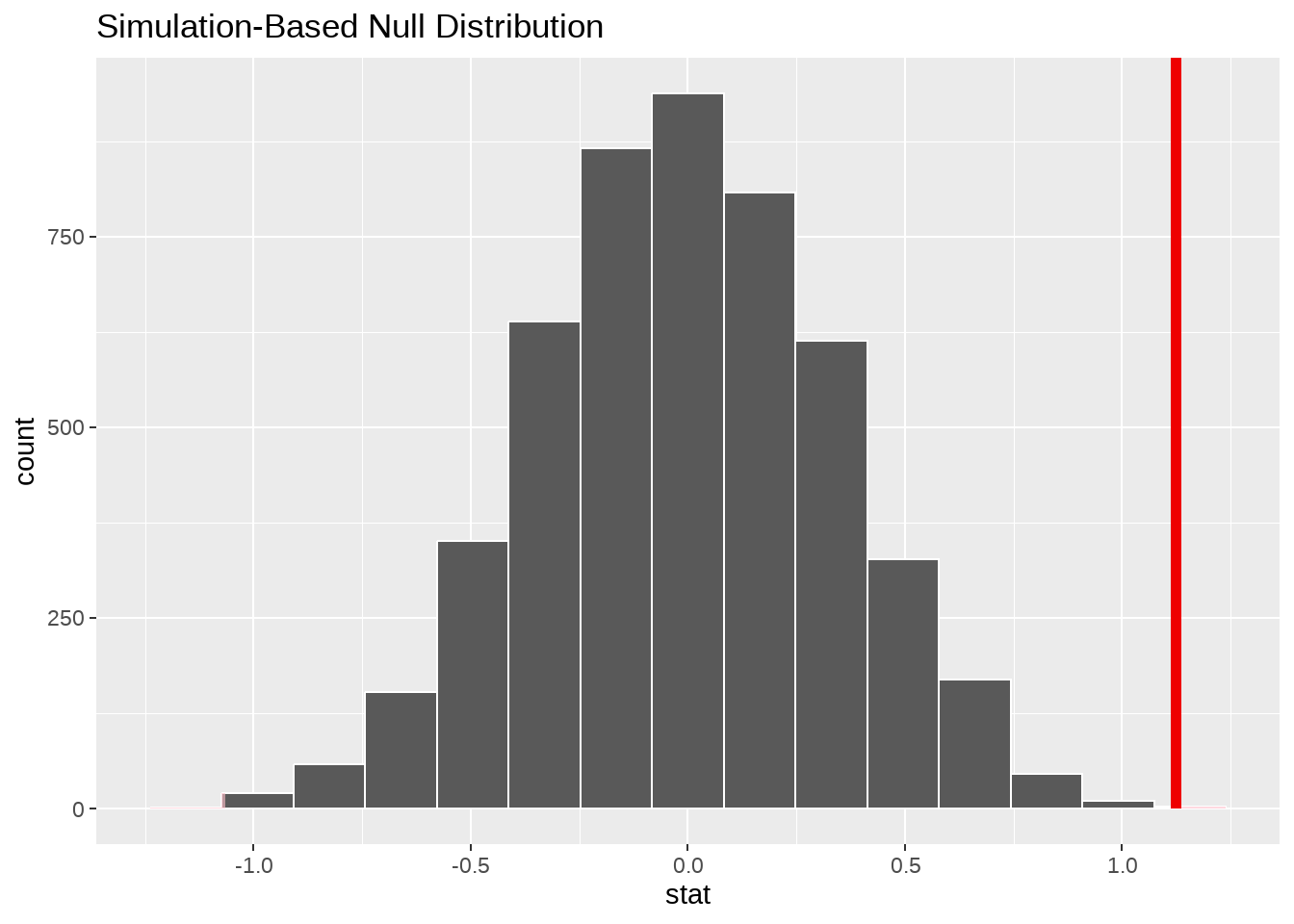
# shade_p_value(bins = 100, obs_stat = obs_diff, direction = "both")- 计算p值
pvalue <- null_dist %>%
get_pvalue(obs_stat = obs_diff, direction = "two_sided")
pvalue## # A tibble: 1 × 1
## p_value
## <dbl>
## 1 0.0008- 结论
在构建的虚拟(\(\Delta = 0\))的平行世界里,出现实际观察值(1.1235294)的概率为(8^{-4})。 如果以(p < 0.05)为标准,我们看到p_value < 0.05, 那我们有足够的证据证明,H0不成立,即爱情电影和动作电影的评分均值存在显著差异,具体来说,动作电影的平均评分要比爱情电影低些。
56.2 案例2: 航天事业的预算有党派门户之见?
美国国家航空航天局的预算是否存在党派门户之见?
gss <- read_rds("./demo_data/gss.rds")
gss %>%
select(NASA, party) %>%
count(NASA, party) %>%
head(8)## # A tibble: 8 × 3
## NASA party n
## <fct> <fct> <int>
## 1 TOO LITTLE Dem 8
## 2 TOO LITTLE Ind 13
## 3 TOO LITTLE Rep 9
## 4 ABOUT RIGHT Dem 22
## 5 ABOUT RIGHT Ind 37
## 6 ABOUT RIGHT Rep 17
## 7 TOO MUCH Dem 13
## 8 TOO MUCH Ind 22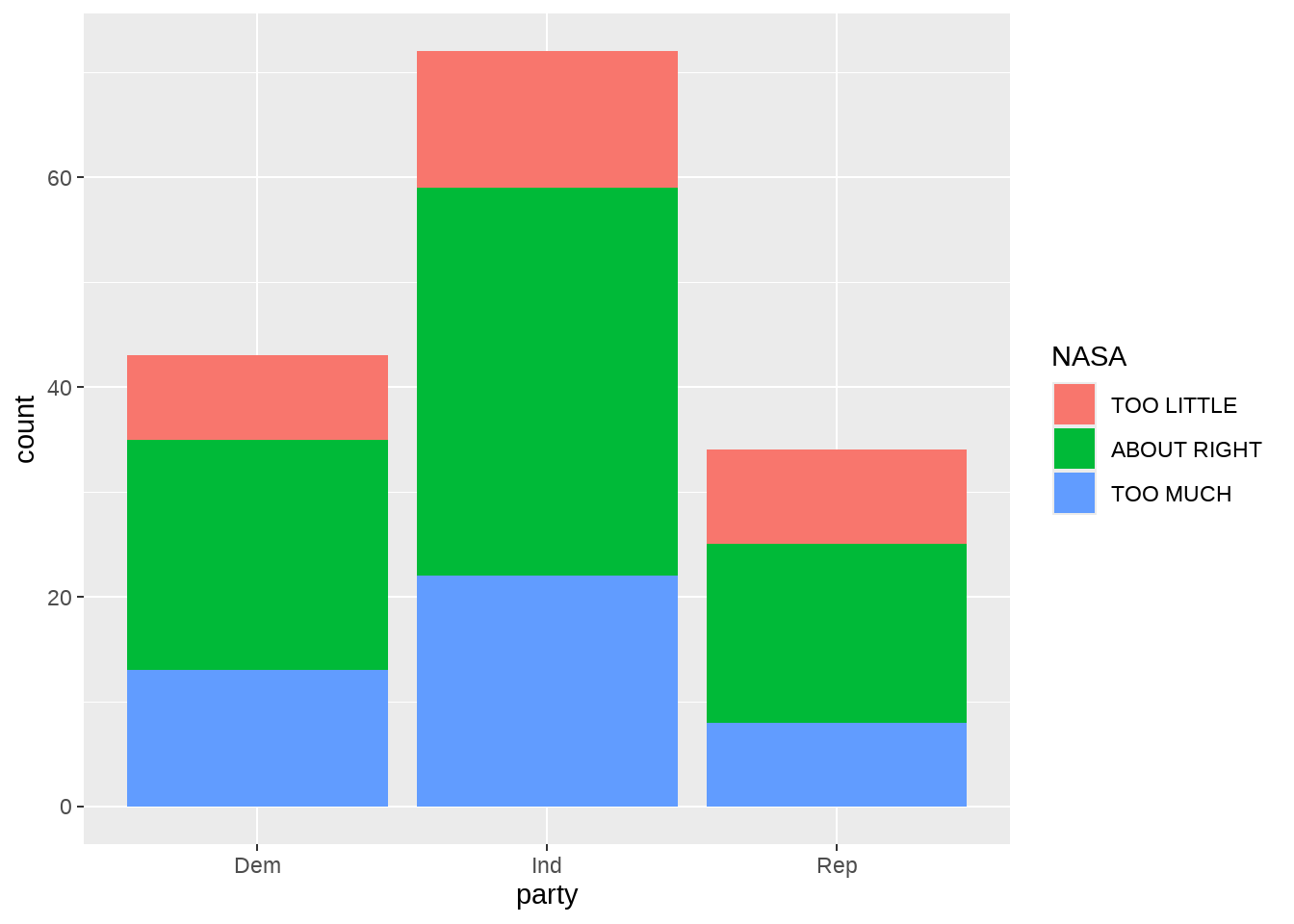
假设:
-
零假设 \(H_0\):
- 不同党派对预算的态度的构成比(TOO LITTLE, ABOUT RIGHT, TOO MUCH) 没有区别
-
备选假设 \(H_a\):
- 不同党派对预算的态度的构成比(TOO LITTLE, ABOUT RIGHT, TOO MUCH) 存在区别
两种可能的结论:
- 拒绝 \(H_0\)
- 不能拒绝 \(H_0\)
56.2.1 传统的方法
chisq.test(gss$party, gss$NASA)##
## Pearson's Chi-squared test
##
## data: gss$party and gss$NASA
## X-squared = 1.3261, df = 4, p-value = 0.8569或者
## [1] 0.856938856.2.2 infer:Simulation-based tests
## Response: NASA (factor)
## Explanatory: party (factor)
## # A tibble: 1 × 1
## stat
## <dbl>
## 1 1.33
null_dist <- gss %>%
specify(NASA ~ party) %>% # (1)
hypothesize(null = "independence") %>% # (2)
generate(reps = 5000, type = "permute") %>% # (3)
calculate(stat = "Chisq") # (4)
null_dist## Response: NASA (factor)
## Explanatory: party (factor)
## Null Hypothesis: independence
## # A tibble: 5,000 × 2
## replicate stat
## <int> <dbl>
## 1 1 1.29
## 2 2 4.39
## 3 3 1.56
## 4 4 2.00
## 5 5 4.18
## 6 6 3.73
## 7 7 3.96
## 8 8 5.30
## 9 9 9.32
## 10 10 5.67
## # ℹ 4,990 more rows
null_dist %>%
visualize() +
shade_p_value(obs_stat = obs_stat, method = "both", direction = "right")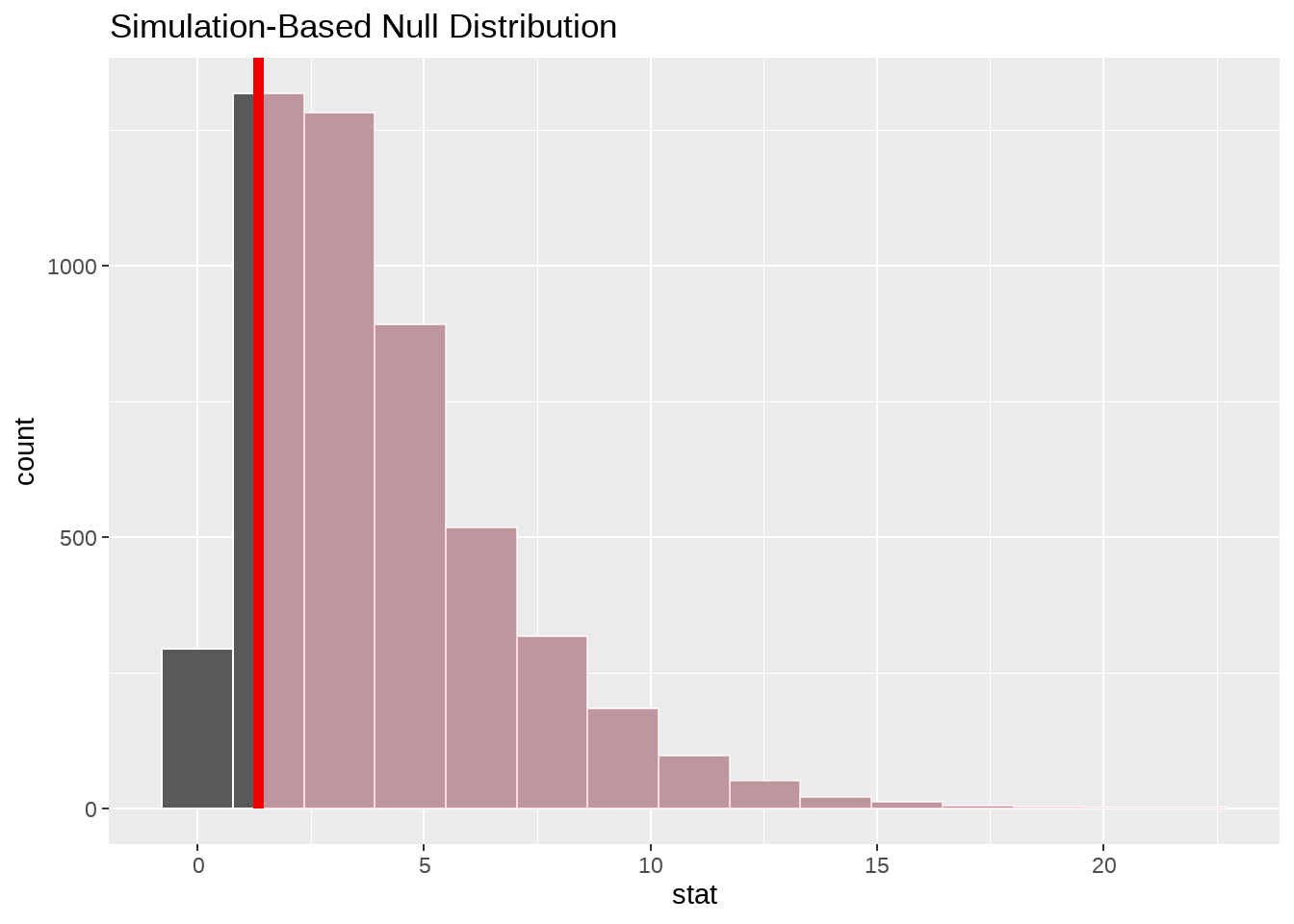
null_dist %>%
get_pvalue(obs_stat = obs_stat, direction = "greater")## # A tibble: 1 × 1
## p_value
## <dbl>
## 1 0.86看到 p_value > 0.05,不能拒绝 \(H_0\),我们没有足够的证据证明党派之间有显著差异

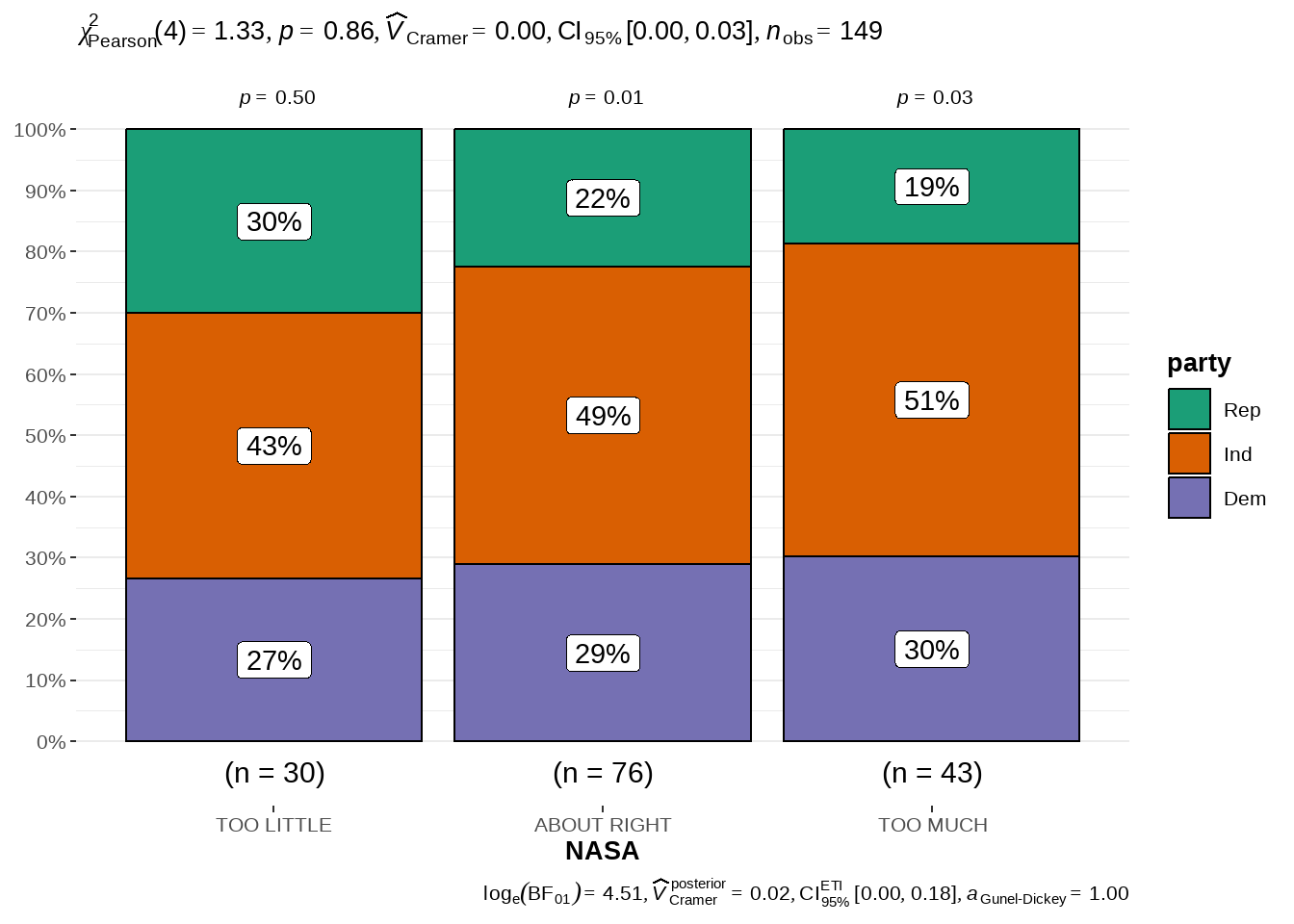
56.2.3 using ggstatsplot::ggbarstats()
library(ggstatsplot)
gss %>%
ggbarstats(
x = party,
y = NASA
)
56.3 案例3:原住民中的女学生多?
案例 quine 数据集有 146 行 5 列,包含学生的生源、文化、性别和学习成效,具体说明如下
- Eth: 民族背景:原住民与否 (是”A”; 否 “N”)
- Sex: 性别
- Age: 年龄组 (“F0”, “F1,” “F2” or “F3”)
- Lrn: 学习者状态(平均水平 “AL”, 学习缓慢 “SL”)
- Days:一年中缺勤天数
## # A tibble: 146 × 5
## Eth Sex Age Lrn Days
## <fct> <fct> <fct> <fct> <int>
## 1 A M F0 SL 2
## 2 A M F0 SL 11
## 3 A M F0 SL 14
## 4 A M F0 AL 5
## 5 A M F0 AL 5
## 6 A M F0 AL 13
## 7 A M F0 AL 20
## 8 A M F0 AL 22
## 9 A M F1 SL 6
## 10 A M F1 SL 6
## # ℹ 136 more rows从民族背景有两组(A, N)来看,性别为 F 的占比 是否有区别?
## # A tibble: 4 × 3
## Eth Sex n
## <fct> <fct> <int>
## 1 A F 38
## 2 A M 31
## 3 N F 42
## 4 N M 3556.3.1 传统方法
##
## 2-sample test for equality of proportions without continuity correction
##
## data: table(td$Eth, td$Sex)
## X-squared = 0.0040803, df = 1, p-value = 0.9491
## alternative hypothesis: two.sided
## 95 percent confidence interval:
## -0.1564218 0.1669620
## sample estimates:
## prop 1 prop 2
## 0.5507246 0.545454556.3.2 基于模拟的方法
被解释变量 sex 中F的占比,解释变量中两组(A,N)
obs_diff <- td %>%
specify(Sex ~ Eth, success = "F") %>%
calculate(
stat = "diff in props",
order = c("A", "N")
)
obs_diff## Response: Sex (factor)
## Explanatory: Eth (factor)
## # A tibble: 1 × 1
## stat
## <dbl>
## 1 0.00527
null_distribution <- td %>%
specify(Sex ~ Eth, success = "F") %>%
hypothesize(null = "independence") %>%
generate(reps = 5000, type = "permute") %>%
calculate(stat = "diff in props", order = c("A", "N"))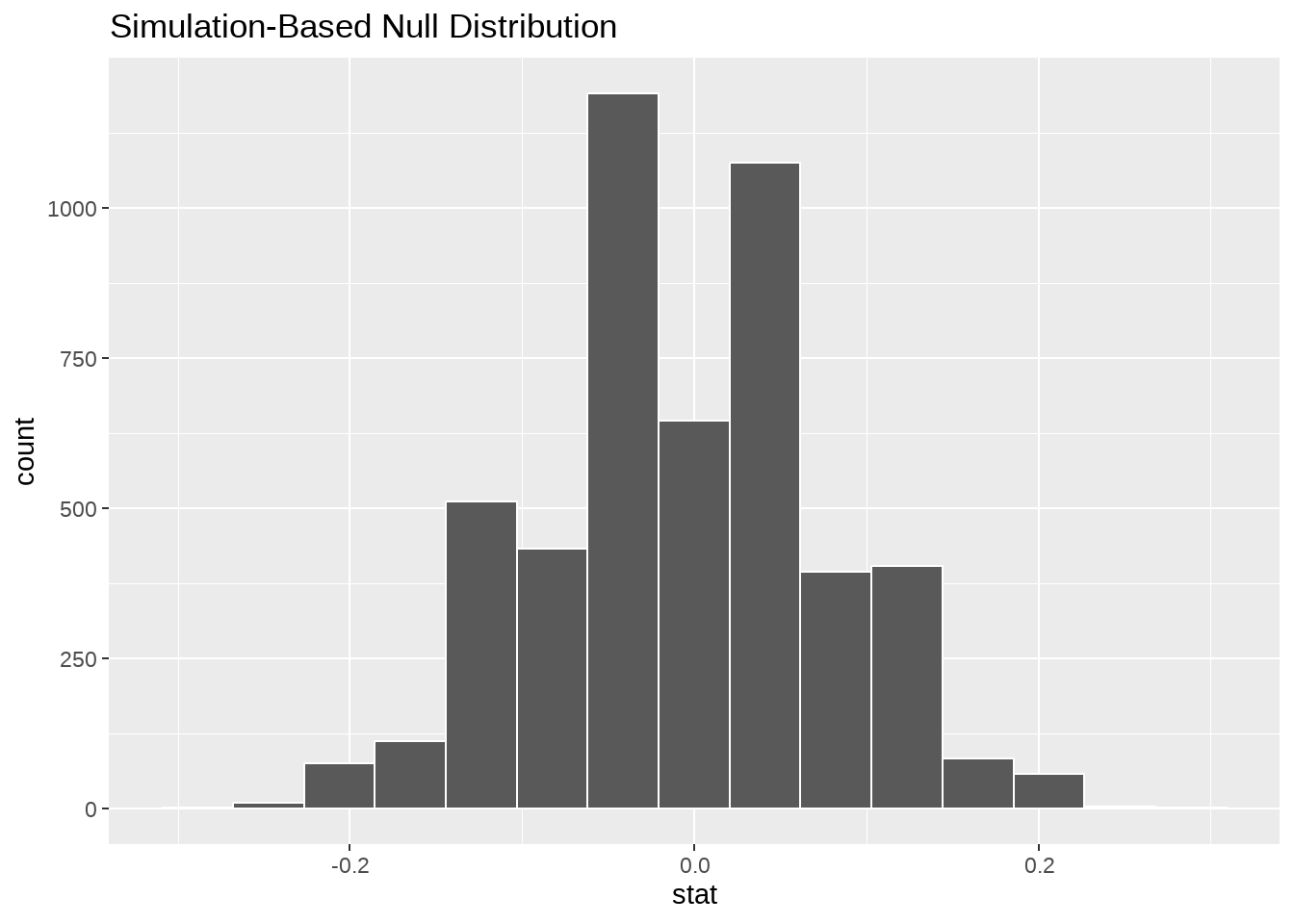
pvalue <- null_distribution %>%
get_pvalue(obs_stat = obs_diff, direction = "both")
pvalue## # A tibble: 1 × 1
## p_value
## <dbl>
## 1 1## # A tibble: 1 × 2
## lower_ci upper_ci
## <dbl> <dbl>
## 1 -0.160 0.170
56.4 宏包infer
我比较喜欢infer宏包的设计思想,它把统计推断分成了四个步骤

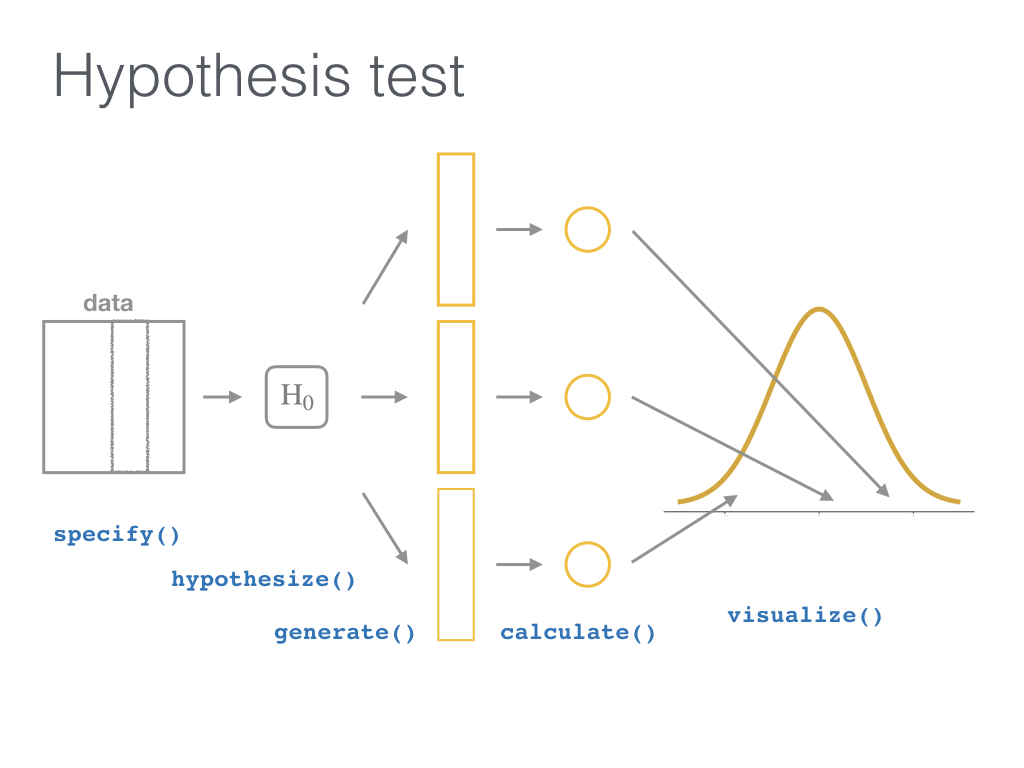
specify()指定解释变量和被解释变量 (y ~ x)hypothesize()指定零假设 (比如,independence=y和x彼此独立)-
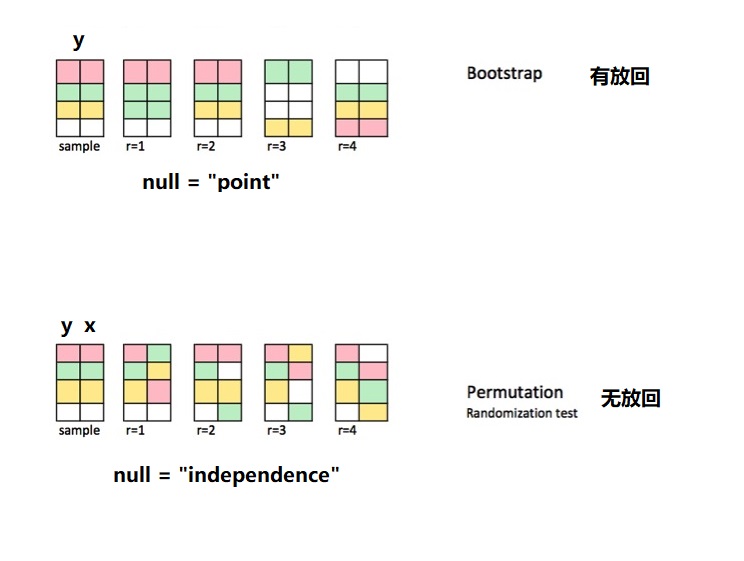
generate()从基于零假设的平行世界中抽样:- 指定每次重抽样的类型,通俗点讲就是数据洗牌,重抽样
type = "bootstrap"(有放回的),对应的零假设往往是null = “point” ; 重抽样type = "permuting"(无放回的),对应的零假设往往是null = “independence”, 指的是y和x之间彼此独立的,因此抽样后会重新排列,也就说原先 value1-group1 可能变成了value1-group2,(因为我们假定他们是独立的啊,这种操作,也不会影响y和x的关系) - 指定多少组 (
reps = 1000)
- 指定每次重抽样的类型,通俗点讲就是数据洗牌,重抽样
calculate()计算每组(reps)的统计值 (stat = "diff in props")visualize()可视化,对比零假设的分布与实际观察值.