Skip to main content

数据科学中的 R 语言

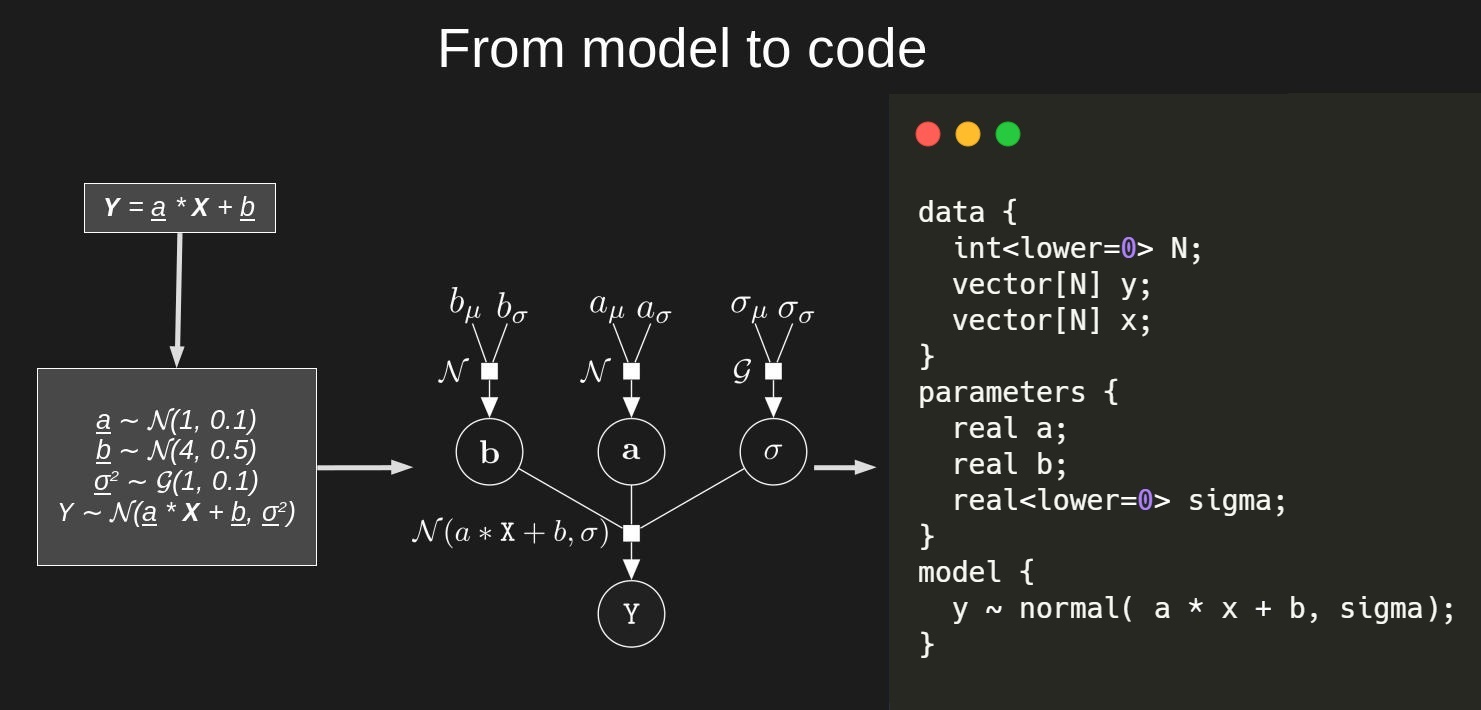
第 66 章 贝叶斯线性回归

66.1 加载宏包 

library(tidyverse)
library(tidybayes)
library(rstan)
rstan_options(auto_write = TRUE)
options(mc.cores = parallel::detectCores())

66.2 案例

数据是不同天气温度冰淇淋销量，估计气温与销量之间的关系。

icecream <- data.frame(
  temp = c( 11.9, 14.2, 15.2, 16.4, 17.2, 18.1, 
         18.5, 19.4, 22.1, 22.6, 23.4, 25.1),
  units = c( 185L, 215L, 332L, 325L, 408L, 421L, 
          406L, 412L, 522L, 445L, 544L, 614L)
  )
icecream
##    temp units
## 1  11.9   185
## 2  14.2   215
## 3  15.2   332
## 4  16.4   325
## 5  17.2   408
## 6  18.1   421
## 7  18.5   406
## 8  19.4   412
## 9  22.1   522
## 10 22.6   445
## 11 23.4   544
## 12 25.1   614
icecream %>% 
  ggplot(aes(temp, units)) + 
  geom_point()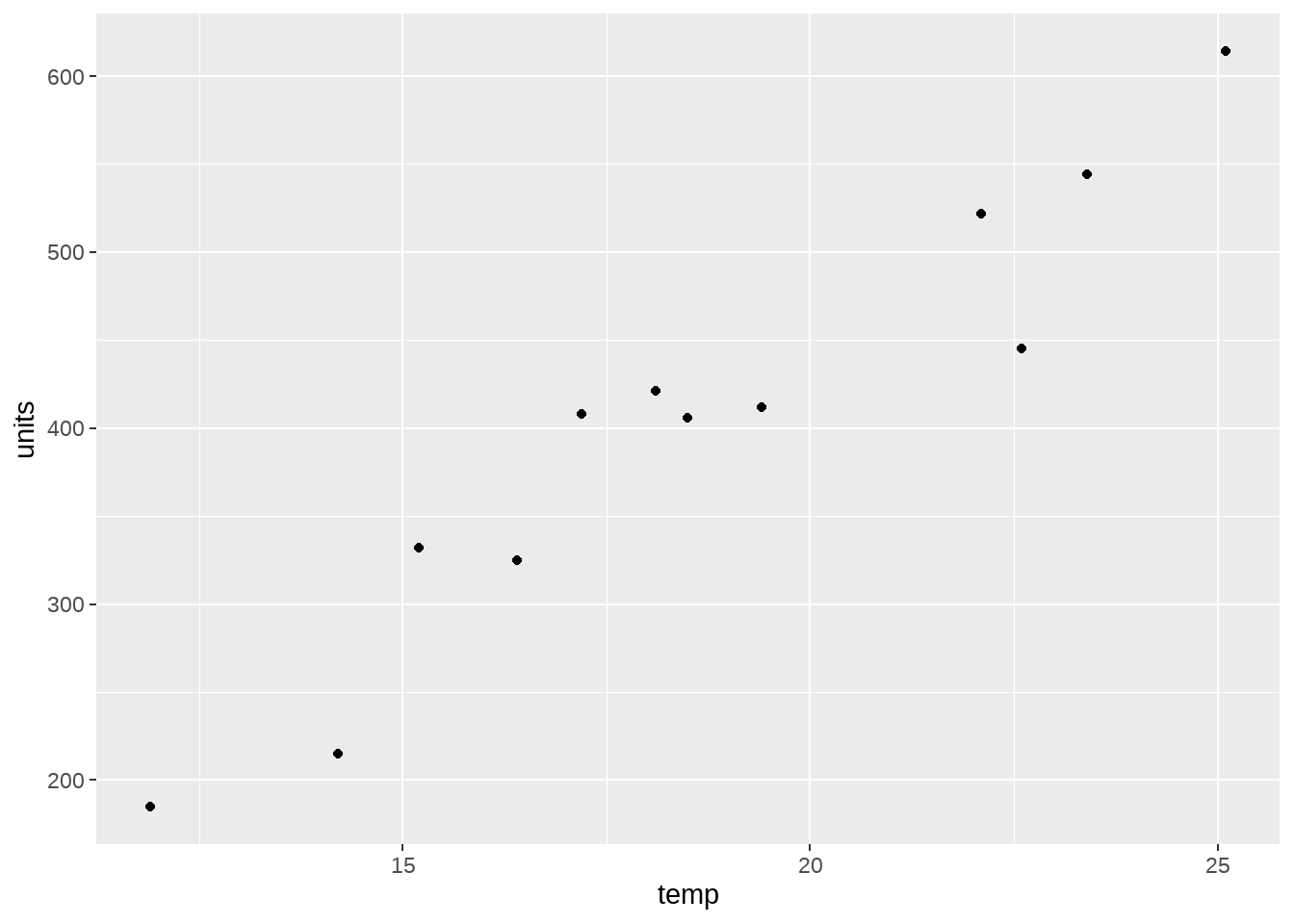
icecream %>% 
  ggplot(aes(units)) + 
  geom_density()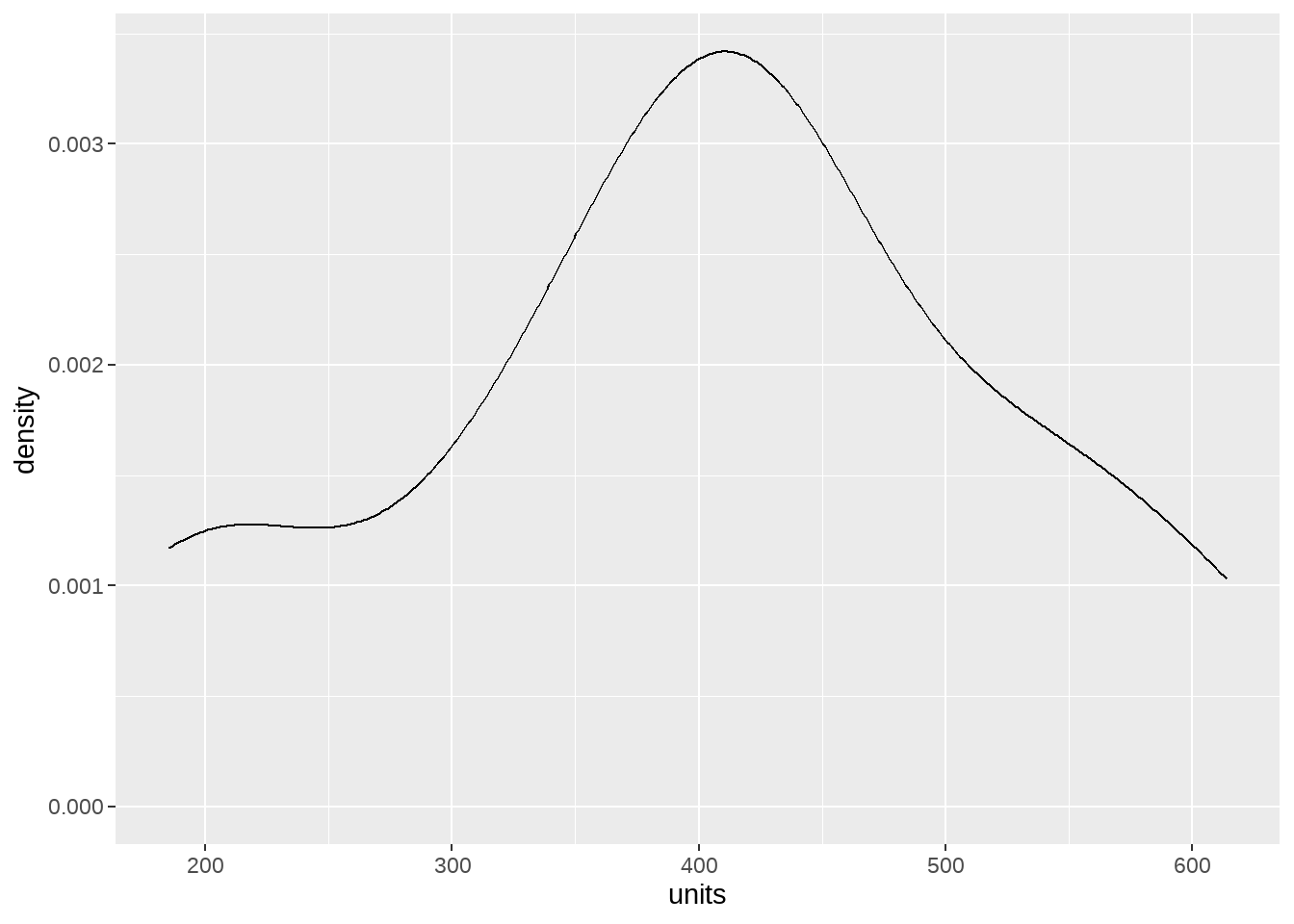

66.2.1 lm() 

fit_lm <- lm(units ~ 1 + temp, data = icecream)

summary(fit_lm)
## 
## Call:
## lm(formula = units ~ 1 + temp, data = icecream)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -75.512 -12.566   4.133  22.236  49.963 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -159.474     54.641  -2.919   0.0153 *  
## temp          30.088      2.866  10.499 1.02e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 38.13 on 10 degrees of freedom
## Multiple R-squared:  0.9168, Adjusted R-squared:  0.9085 
## F-statistic: 110.2 on 1 and 10 DF,  p-value: 1.016e-06
confint(fit_lm, level = 0.95)
##                  2.5 %    97.5 %
## (Intercept) -281.22128 -37.72702
## temp          23.70223  36.47350
# Confidence Intervals
# coefficient +- qt(1-alpha/2, degrees_of_freedom) * standard errors

coef <- summary(fit_lm)$coefficients[2, 1] 
err  <- summary(fit_lm)$coefficients[2, 2]

coef + c(-1,1)*err*qt(0.975,  nrow(icecream) - 2) 
## [1] 23.70223 36.47350

66.2.2 线性模型

线性回归需要满足四个前提假设：

  1. Linearity
    • 因变量和每个自变量都是线性关系
  2. Indpendence
    • 对于所有的观测值，它们的误差项相互之间是独立的
  3. Normality
    • 误差项服从正态分布
  4. Equal-variance
    • 所有的误差项具有同样方差

这四个假设的首字母，合起来就是LINE，这样很好记

把这四个前提画在一张图中

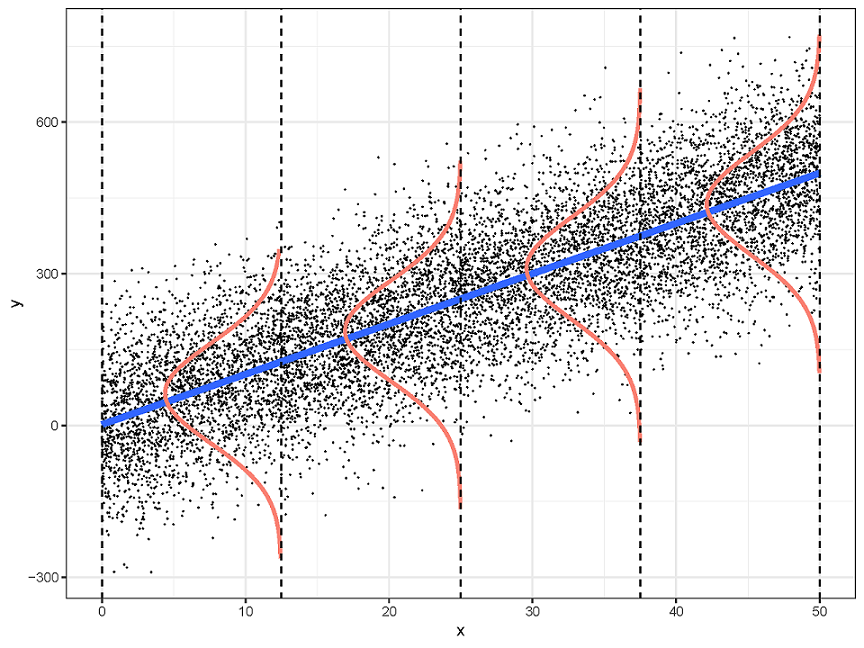
66.2.3 数学表达式

\[ y_n = \alpha + \beta x_n + \epsilon_n \quad \text{where}\quad \epsilon_n \sim \operatorname{normal}(0,\sigma). \]

等价于

\[ y_n - (\alpha + \beta X_n) \sim \operatorname{normal}(0,\sigma), \]

进一步等价

\[ y_n \sim \operatorname{normal}(\alpha + \beta X_n, \, \sigma). \]

因此，我们推荐这样写线性模型的数学表达式 \[ \begin{align} y_n &\sim \operatorname{normal}(\mu_n, \,\, \sigma)\\ \mu_n &= \alpha + \beta x_n \end{align} \]

66.3 stan 代码 

stan_program <- "
data {
  int<lower=0> N;
  vector[N] y;
  vector[N] x;
}
parameters {
  real alpha;
  real beta;
  real<lower=0> sigma;
}
model {
  y ~ normal(alpha + beta * x, sigma);
  
  alpha  ~ normal(0, 10);
  beta   ~ normal(0, 10);
  sigma  ~ exponential(1);
}

"
stan_data <- list(
   N = nrow(icecream),
   x = icecream$temp, 
   y = icecream$units
  )

fit_normal <- stan(model_code = stan_program, data = stan_data)
  • 检查 Traceplot
traceplot(fit_normal)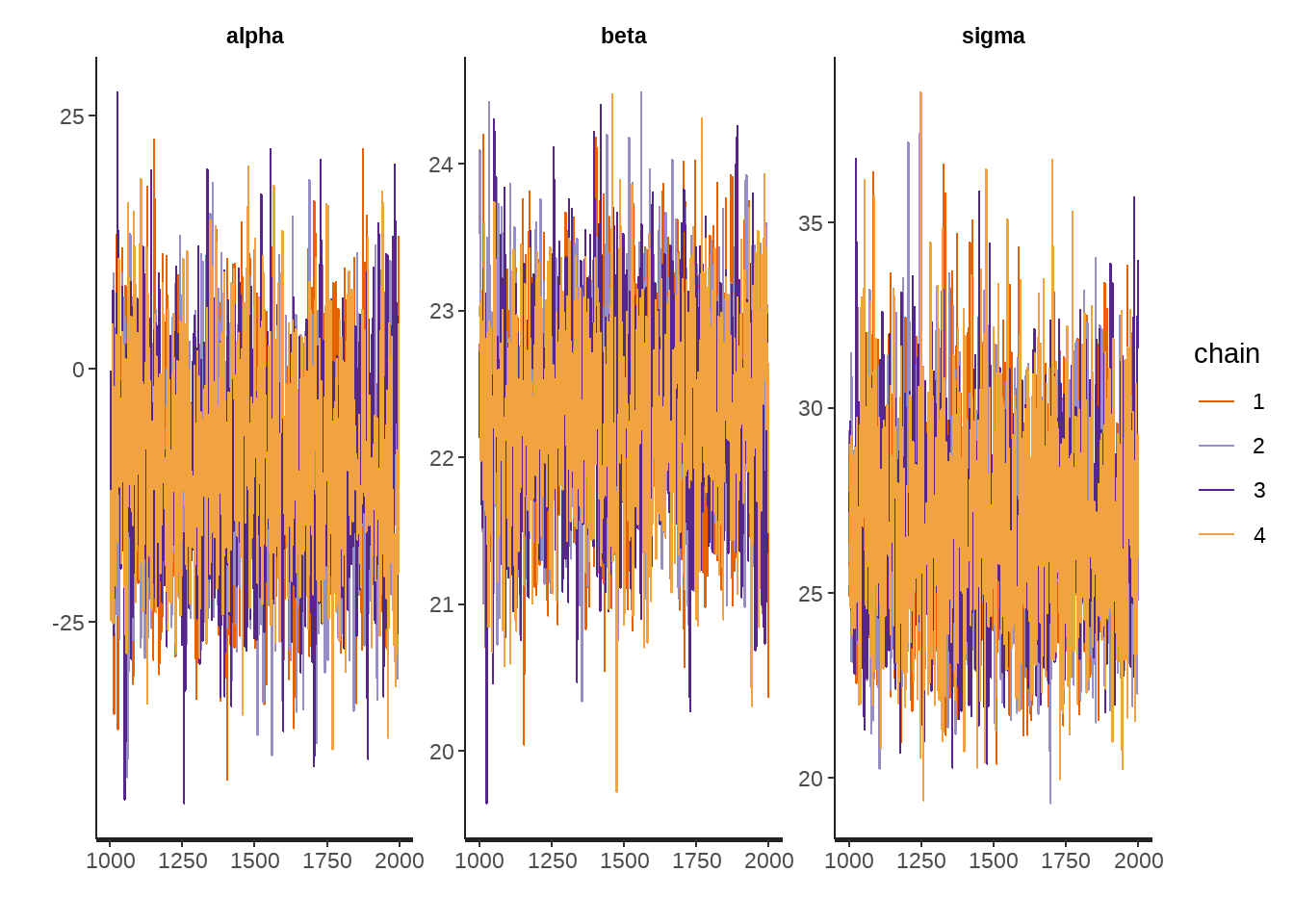
  • 检查结果
fit_normal
## Inference for Stan model: anon_model.
## 4 chains, each with iter=2000; warmup=1000; thin=1; 
## post-warmup draws per chain=1000, total post-warmup draws=4000.
## 
##         mean se_mean   sd   2.5%    25%    50%    75%  97.5% n_eff Rhat
## alpha  -9.07    0.25 9.96 -27.75 -15.75  -9.32  -2.21  10.79  1609    1
## beta   22.33    0.02 0.66  21.06  21.88  22.32  22.79  23.58  1467    1
## sigma  26.86    0.06 2.70  22.06  24.92  26.69  28.58  32.53  2029    1
## lp__  -85.16    0.03 1.25 -88.50 -85.71 -84.85 -84.25 -83.75  1387    1
## 
## Samples were drawn using NUTS(diag_e) at Mon Oct 28 09:47:47 2024.
## For each parameter, n_eff is a crude measure of effective sample size,
## and Rhat is the potential scale reduction factor on split chains (at 
## convergence, Rhat=1).

66.4 理解后验概率

提取后验概率的方法很多

post_samples <- rstan::extract(fit_normal)

post_samples是一个列表，每个元素对应一个系数，每个元素都有4000个样本，我们可以用ggplot画出每个系数的后验分布

tibble(x = post_samples[["beta"]] ) %>% 
  ggplot(aes(x)) +
  geom_density()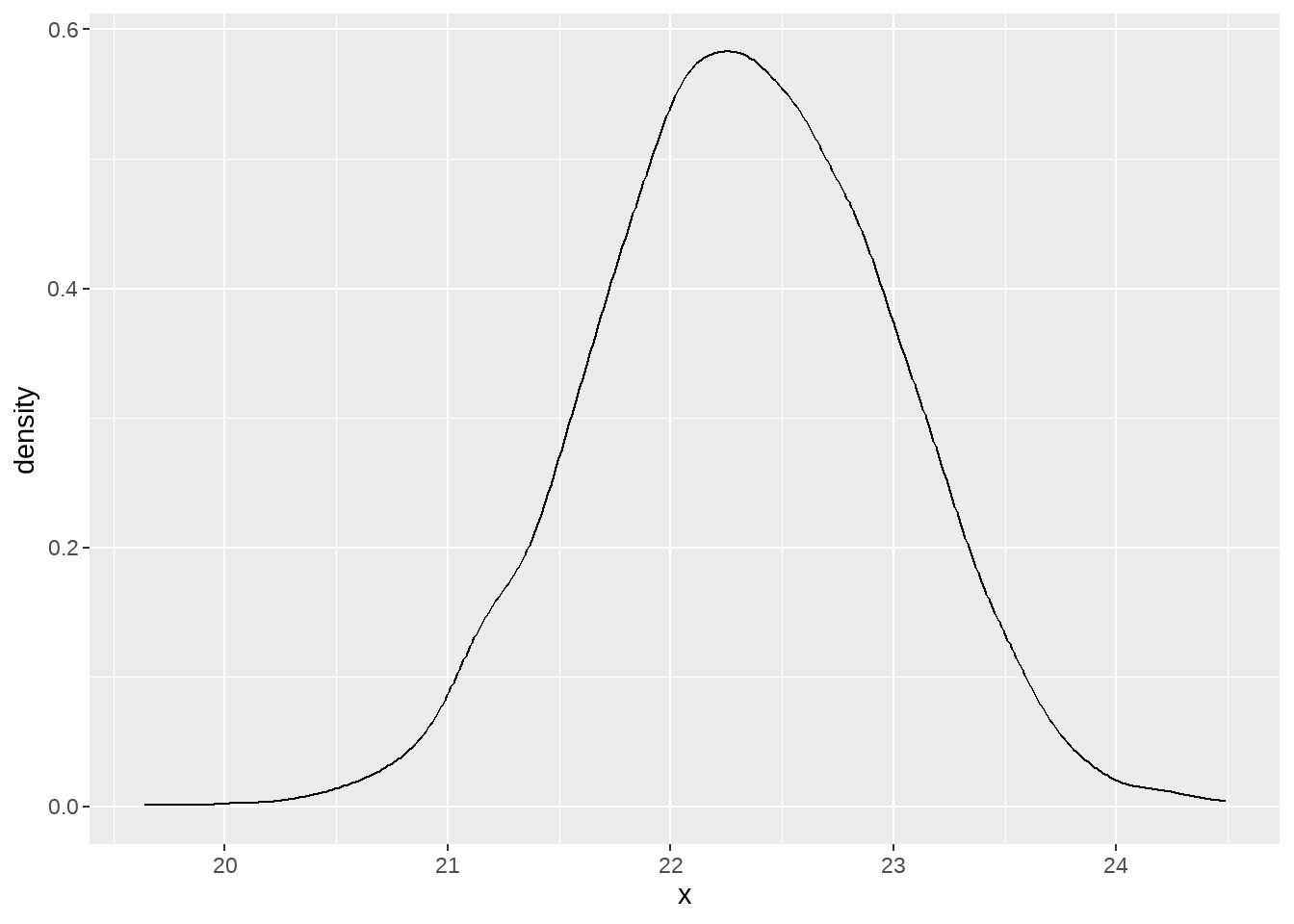
  • 用bayesplot宏包可视化
posterior <- as.matrix(fit_normal)

bayesplot::mcmc_areas(posterior, 
                      pars = c("alpha", "beta", "sigma"),
                      prob = 0.89)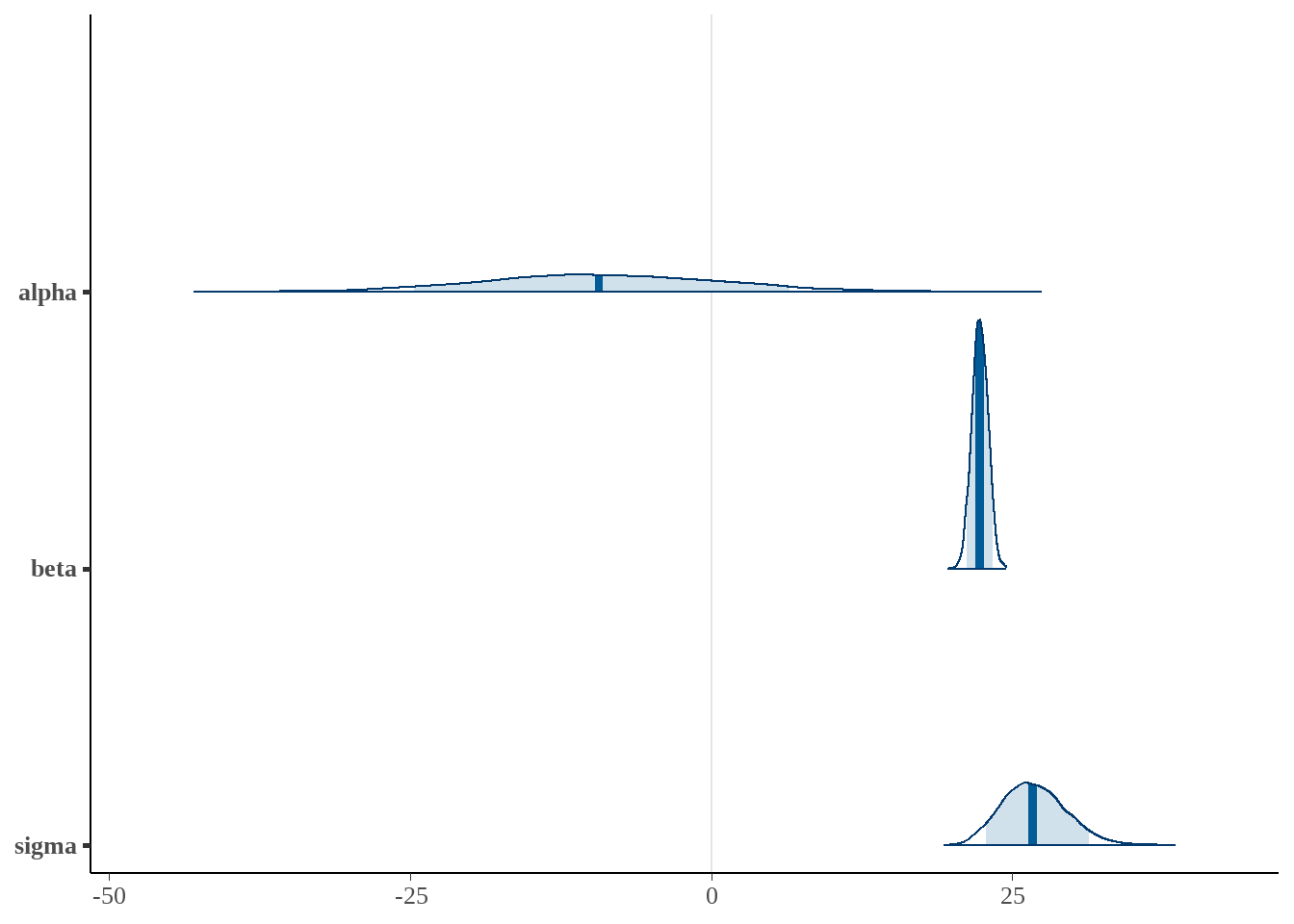
  • 用tidybayes宏包提取样本并可视化，我喜欢用这个，因为它符合tidyverse的习惯
fit_normal %>% 
  tidybayes::spread_draws(alpha, beta, sigma) %>% 
  
  ggplot(aes(x = beta)) +
  tidybayes::stat_halfeye(.width = c(0.66, 0.95)) + 
  theme_bw()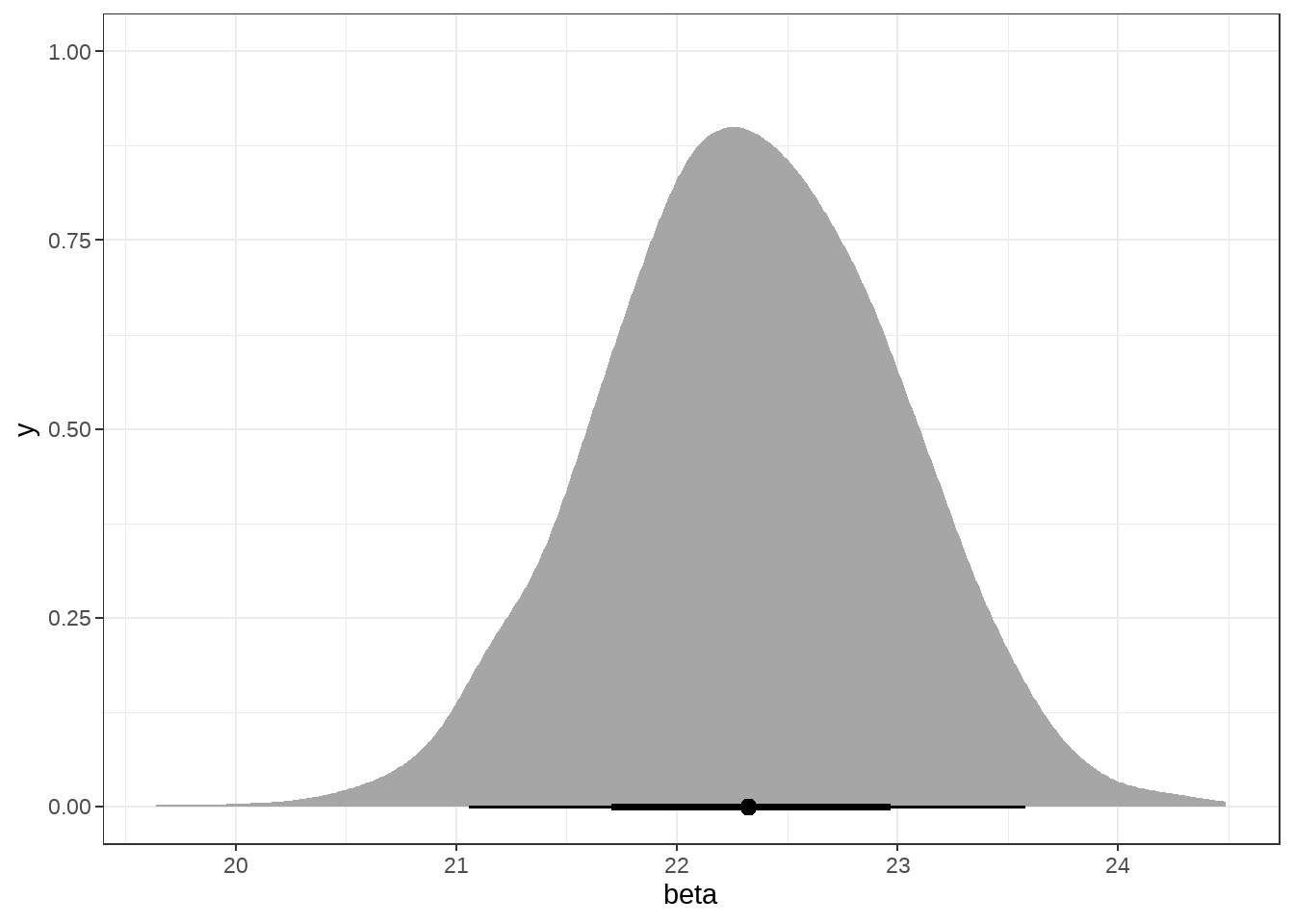 
fit_normal %>% 
  tidybayes::spread_draws(alpha, beta, sigma) %>% 
  
  ggplot(aes(beta, color = "posterior")) + 
  geom_density(size = 1) + 
  
  stat_function(fun = dnorm, 
        args = list(mean = 0, 
                    sd = 10), 
        aes(colour = 'prior'), size = 1) +
  xlim(-30, 30) +
  scale_color_manual(name = "", 
                     values = c("prior" = "red", "posterior" = "black")
                     ) + 
  ggtitle("系数beta的先验和后验概率分布") + 
  xlab("beta")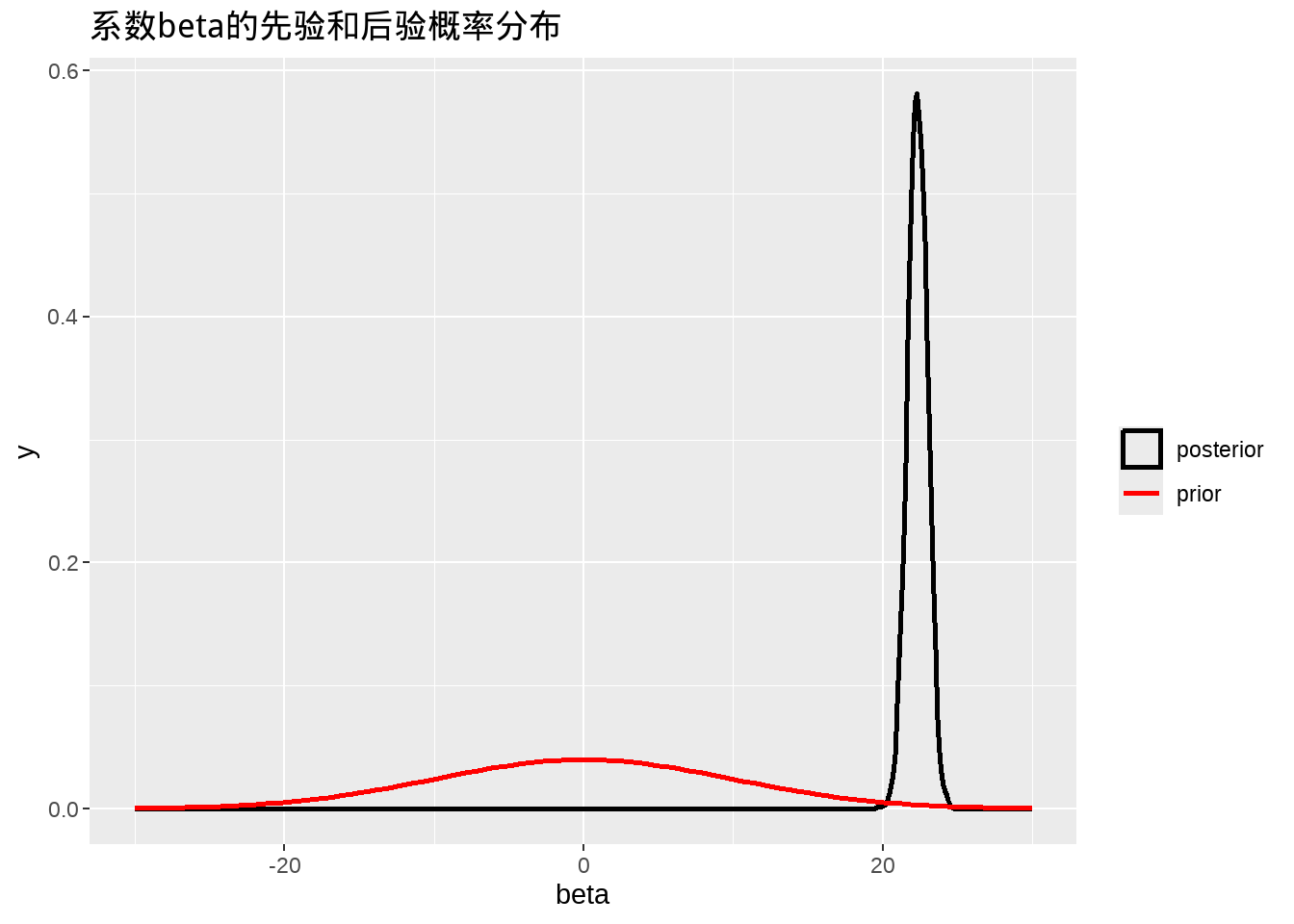

66.5 小结

66.6 作业与思考

  • 去掉stan代码中的先验信息，然后重新运行，然后与lm()结果对比。

  • 调整stan代码中的先验信息，然后重新运行，检查后验概率有何变化。

alpha  ~ normal(100, 5);
beta   ~ normal(20, 5);
  • 修改stan代码，尝试推断上一章的身高分布
d <- readr::read_rds(here::here('demo_data', "height_weight.rds")) 
stan_program <- "
data {
  int N;
  vector[N] y;
}
parameters {
  real mu;
  real<lower=0> sigma;
}

model {
  mu ~ normal(168, 20);
  sigma ~ uniform(0, 50);
  
  y ~ normal(mu, sigma);
}

"

stan_data <- list(
  N = nrow(d),
  y = d$height
)

fit <- stan(model_code = stan_program, data = stan_data,
            iter = 31000, 
            warmup = 30000, 
            chains = 4, 
            cores = 4
            )