8.4 Resolution

For most problems of biological interest (e.g., the shape of the lens of the eye), only the particulate nature of light, especially its rectilinear propagation, is important. This can be thought of as a result of the large size of the elements of biological interest compared to the wavelength of light. For example, for the sun: \(\lambda_m \approx 5 \times 10^{-7}m\) [problem 2a], which is much smaller than the physical dimension of any organism, or even any organ in any organism. Only in certain specialized biological research, for example the investigation of cell ultrastructure, does the wavelength of light become a limiting factor. As the dimensions of the cellular constituents approximate that of light, instruments capable of observing at shorter wavelengths (e.g. electron microscopes) are required.

There is at least one other area of biology where the physical dimensions of the objects of interest are small enough that the wave nature of light becomes an important consideration: the resolution of incoming radiation by sense organs.

The term resolution is used here to denote the ability to distinguish two objects. That is, how close together must two objects be before they appear as a single object to the organism? Clearly, this depends to some extent on the organism in question; eagles resolve better than do moles. Also, the limit of resolution will be affected by the experience of the observer. Nevertheless, it is useful to have some rough comparison of the resolving ability of various systems, and for this purpose Rayleigh’s criterion is most often employed.

Rayleigh’s criterion is derived from the theory of Fresnel diffraction by a circular opening (for a derivationand detailed discussion, see Elmore & Heald 1969). Qualitatively, this criterion is seen to be a measure of the relative overlap of the diffraction patterns of the images of objects on the focal plane of the observer. More specifically, it is a measure of the displacement of the central maxima of these diffraction patterns. Two images are said to be just resolved when the central maximum of one diffraction pattern falls on the first minimum of the other (see Fig. 8.3). From Figure 8.3, it can be seen that the limit of resolution is some distance \(\delta x\) between the two images on the focal plane, or alternatively some angle \(\delta\theta\) between the central axis of the lens and the ray connecting the center point of the lens to the centers of the principal maxima on the focal plane [\(p_i^\prime\),\(p_2^\prime\) of Fig. 8.3]. Therefore, in comparing the resolving power of different instruments the reciprocal of these quantities should be used (i.e., \(1/\delta x\) or \(1/\delta\theta\)), so that the “more powerful” instrument is able to distinguish objects which are unresolved by the “less powerful” instrument. For a distant object, the objective (lens) is the aperture which creates the circular diffraction. The mathematical details of Fresnel diffraction lead to the result that the position of the first minimum relative to the principal maximum will be:

\[\begin{equation} \sin \alpha=0.61\lambda/r \tag{8.11} \end{equation}\] where \(\lambda =\) the wavelength of radiation which forms the image,
\(r=\) the radius of the objective,
\(\alpha=\) the angle between the images of the objects.

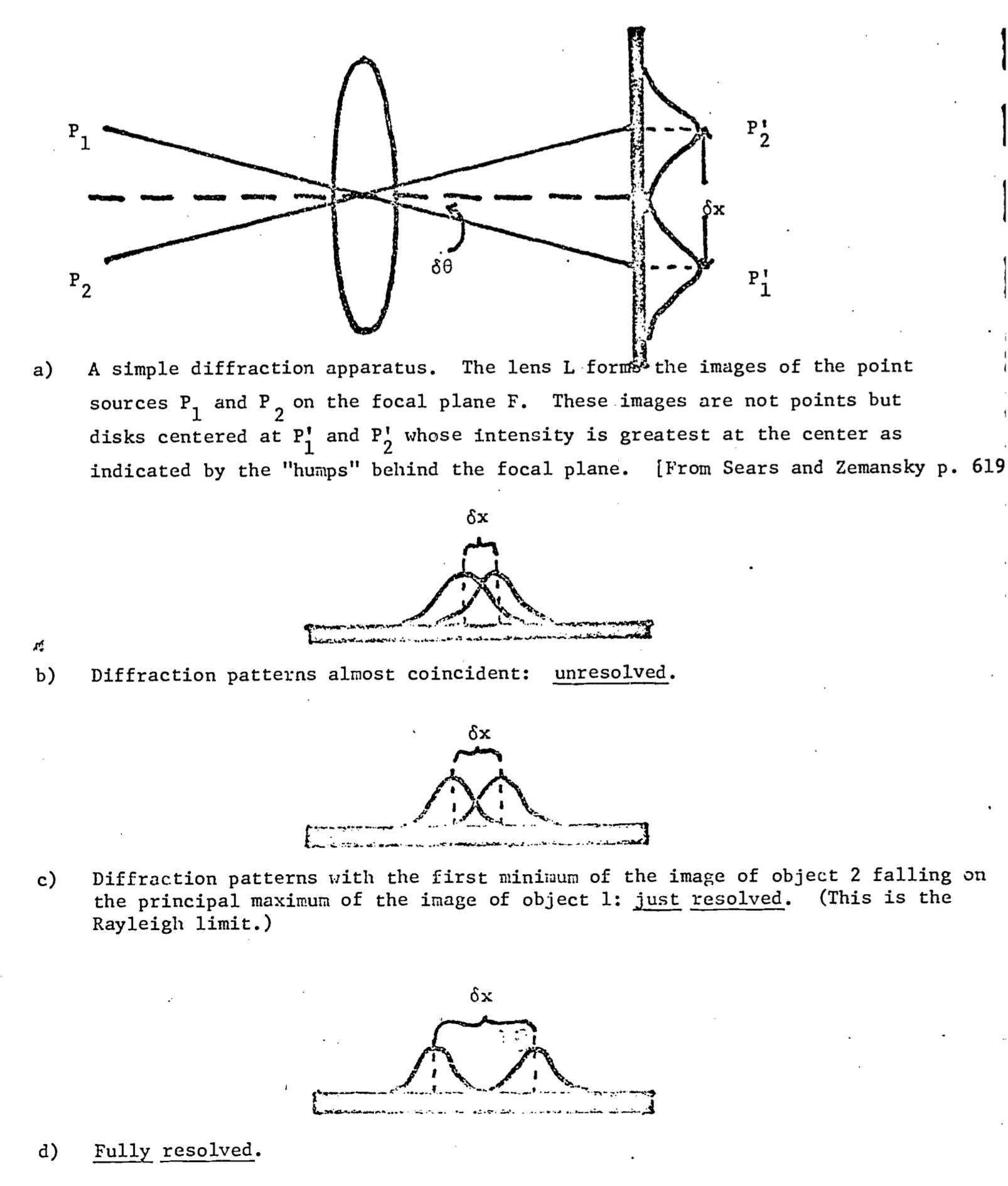
Figure 8.3: The Rayleigh criterion: Fresnel diffraction by circular aperture.

The limit to resolution given by Eq. (8.12) is known as Rayleigh’s criterion. Using the familiar (Taylor) expansion of the sine function one finds that: \[\sin\alpha=\alpha-\alpha^3+\alpha^5-\alpha^7+...\] or \[\sin\alpha=\alpha+0(\alpha^3).\] Here \(0(\alpha^3)\) means terms of order (size) strictly less than \(\alpha^3\). If \(\alpha\) is small, then \(\alpha^3\) is very small and one can make the small angle approximation \[\sin\alpha \approx \alpha\] which when substituted into Eq. (8.11) yields: \[\begin{equation} \alpha=0.61\lambda/r \tag{8.12} \end{equation}\] Rayleigh’s criterion in the simple form of Eq. (8.12) is a powerful tool in an analysis by the biologist of the evolution of sense organs. In particular, such questions as the scaling of eye size with organismal size (e.g., why are a whale’s eyes the same size as those of a cow?), or the cellular organization of the organs themselves (e.g. the distribution of cones on the retina) have relatively simple answers when analyzed in this way. The ramifications of this analysis are explored in the following examples and problems.

Example 4

From the Rayleigh criterion, the results of problem 2a, and the fact that in bright daylight the diameter of the human pupil is \(\approx\) 2.0 mm, determine the resolution of the human eye in minutes of arc. What does this resolution limit correspond to at 10 m?

Solution:
\(\lambda_m=5.08\times10^{-7}m\) (from prob. 2a)
\(r=1.0mm=1.0\times10^{-3}m\)

Putting these parameters into the formula for the Rayleigh criterion,
Eq. (8.12), we get:

\[\begin{align*} \alpha &=0.61\lambda/r \\ &=0.61(5.08\times10^{-7}m)/(1.0\times10^{-3}m) \\ &=3.1\times10^{-3}\text{radians} \end{align*}\]

Since \(2\pi\) radians \(=360^\circ = 2.16 \times 10^4\) min, we know that 1 radian \(\approx 3.43 \times 10^3\) min. So \[\begin{align*} \alpha&=(3.1\times10^3\mbox{ min/rad})(3.1\times10^{-3}rad) \\ &\approx 1\mbox{ min of arc} \end{align*}\]

At 10m this angle will correspond to an object separation of: \[\begin{align*} \alpha&=S_0/d \\ \text{where } S_0&=\text{separation} \\ d&=\text{distance} \end{align*}\]

\[\begin{align*} \mbox{or } S_0 = \alpha d &= (3.17\times10^{-4})(10m)=3.117\times10^{-3} \\ &= 3.17mm \end{align*}\]

Thus, in daylight the human eye can just barely resolve two objects which are 3.17 mm apart from one another and 10m distant.

It should be noted at this point that the Rayleigh criterion is a theoretical limit which is rarely approached in practice. For instance, if one used this formula to calculate the separation resolvable by the human eye at 20 feet, it would be smaller than the actual minimum separation resolvable by a person with “normal” (20:20) eyesight.

The cones of the human eye happen to be maximally sensitive to the wavelength \(\lambda_m\) which corresponds to the maximum of the sun’s energy density spectrum. Using Rayleigh’s criterion and the fact that the retina is \(\approx\) 17 mm behind the first nodal point (which acts as the circular aperture in this case), we can compute the maximum resolution on the surface of the retina.

\[\begin{equation} \delta x=5.4\times10^{-6}m \tag{8.13} \end{equation}\]

Anatomists have determined that the diameter of a retinal cone cell (which mediates color vision) is about \(3.0 \times 10^{-6}m\). The separation between densely packed cone cells is smaller than the limit in Eq. (8.13). Thus thinner cones will not produce higher visual acuity. The resolution is constrained by the physical parameters of the optical system.

Since the eyes of all vertebrates are constructed from the same design, the same physical dimensions that determine the resolution of the human eye will determine resolution throughout the sub-phylum. It is the absolute, not relative, size of the physical components of the optical system which constrain resolution. If the diameters of cone cells are at present at the minimum which is biologically feasible, then a slight increase in the other dimensions of the human eye will give greater resolving power, but beyond a point \((\delta x = 3.0 \times 10^{-6}m)\), there is no payoff in visual acuity for larger eyes.

The eyes of birds of prey show structural alterations which are an evolutionary response to the need for greater resolving power. The retinal cone cells become rod-like, which decreases their diameter, increases their density on the retina and decreases their ability to discriminate color. Furthermore, the retinae from these birds have several pits or foveae. Although the density of light sensitive cells is the same in the foveae as on the rest of the retina, the image is formed on a concave rather than flat surface. Thus the “effective” cone density in the foveae is higher than for the rest of the retina, and so is the resolving power. The combination of these two changes results in increased visual acuity for these avian eyes.

Rayleigh’s criterion is also useful in elucidating the constraints on the design of a quite different sort of eye, the compound eye found in insects and certain crustacea. Each eye is composed of many (up to \(3 \times 10^{-4}\)) simple eyes, called ommatidia (See e.g. Bjorn 1976. p. 92). The shape of the compound eye is roughly that of a half-sphere of radius \(R\), with the lenses of the ommatidia comprising its surface. An estimate of the size of the openings of the ommatidia is calculated in the following example.

Ommatidial Openings

A simple model of an ommatidium is that of a cone with its apex at the center of the half-sphere which forms the eye, and its opening at the surface of the eye. Assume that the angle of the cone is equal to the limiting angle of the Rayleigh formula. Show that the calculated limiting size of the opening to the ommatidia is given as: \[d=(1.22R\lambda)^{1/2}\] If \(\lambda\) = 400 nm, which is the center of the spectrum to which a bee is sensitive, and \(R\) is about 1 mm, what is the optimal size of the ommatidial opening?
Answer:
\[d=2.2\times10^{-5}m=22\mu\]

The actual mean measured opening for a bee is \(20.9\mu\) (Barlow 1952, p. 671). A diagram comparing the observed size of the ommatidia to the value predicted by theory is presented in Fig. 8.4. Rayleigh’s criterion for the limit of resolution of an optical instrument can be extended to interferometers as well. Basically, an interferometer consists of two detectors with the ability to detect phase information separated by a distance \(D\). When the phase information from the two detectors is compared, the resolution of the total system is the same as that of a single detector whose diameter is equal to \(D\). Although a rigorous argument demonstrating this result would not be appropriate here (it is essentially the same as the derivation of Rayleigh’s criterion), a qualitative argument may be useful. Basically, the (diffraction patterns illustrated in Fig. 8.3 are the result of the interference between light waves of different phases, caused by passage of the light through the aperture. The eye sees the interference caused by phase differences as variations in intensity, as illustrated in Fig. 8.3 b, c, d. to an interferometer the signals of the two detectors are compared to reveal phase differences and so the identical resolution criterion applies.

Most vertebrates are able to detect phase differences between ears, so that the interferometer is the correct model for calculating resolution. A consideration of Rayleigh’s criterion shows that if all other parameters remain constant, the greater the separation of the detectors, the greater the resolving power of the system. Many organisms have optimized their ability to locate sound sources by maintaining a maximal separation between the ears. Another biological application of interferometers is illustrated in the following problem.

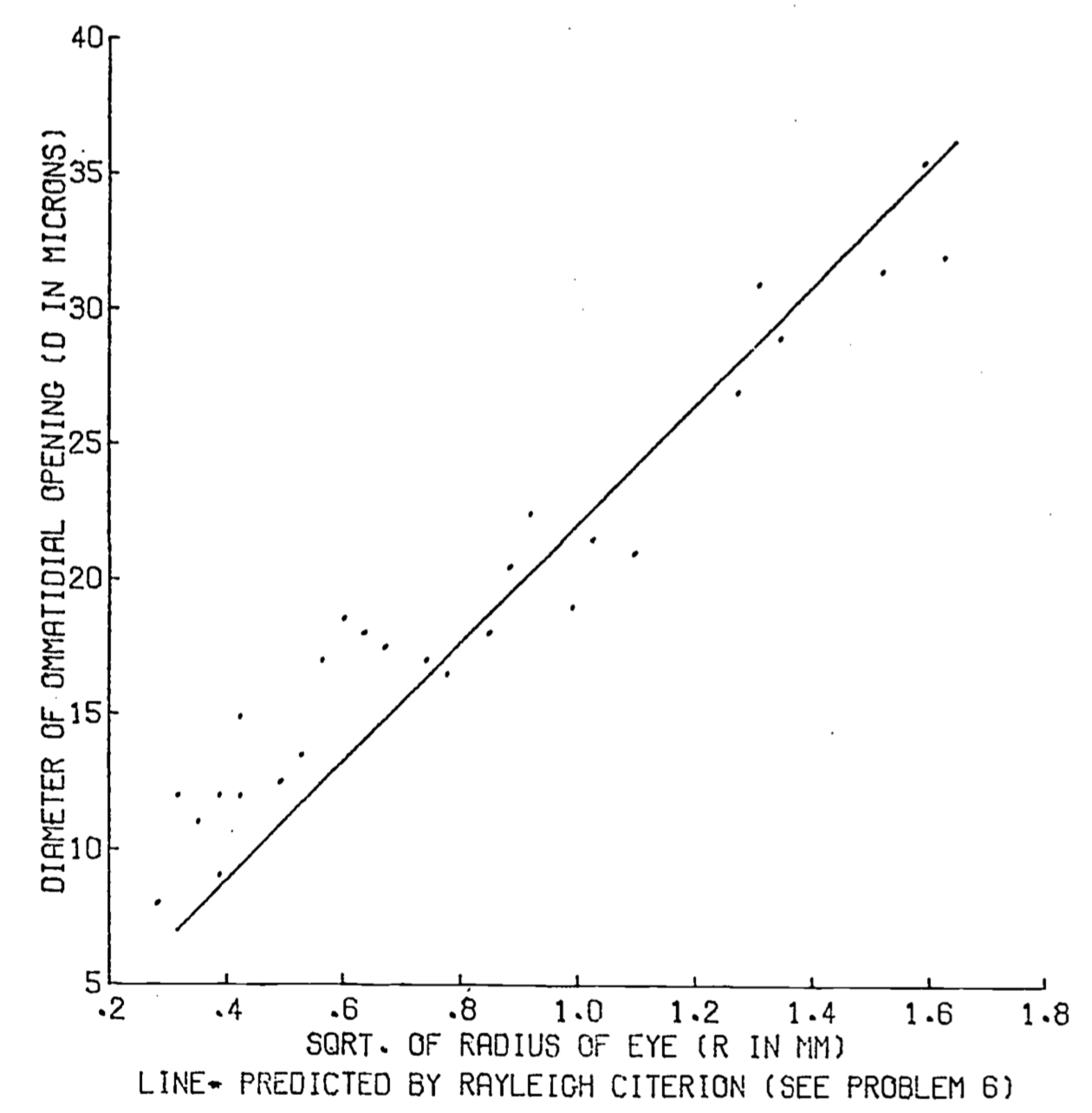
Figure 8.4: Insect eye - ommatidial diameter vs. the squareroot of eye radii. Points are 27 observations on hymenoptera (Barlow 1952).