12.4 Heat Transfer by Conduction Within the Animal

Heat is conducted between the surface of the animal and the body core with the direction determined by the relative temperatures of the animal’s core and surface. Heat transfer can be modeled by approximating the animal as a series of concentric cylinders (Figure 12.1). Within the animal’s core, metabolic heat production is offset by respiratory moisture loss to determine the animal’s core body temperature \(T_b\). We additionally indicate the skin (\(T_s\)), fat layer (\(T_f\)), hair tip (\(T_h\)), and air (\(T_a\)) temperatures.

Heat is conducted within the animal based on the thickness of each layer. Boundary layer thickness, which determines rates of conduction, is proportional to the two-roots root of the diameter of the animal and is influenced by surface roughness, shape, and orientation. The distances from the core are indicated by the radii of cylinders corresponding to the body (\(r_b\)), skin (\(r_s\)), and hair tips (\(r_h\)).

The thickness of the boundary layer varies inversely with the one-third root of wind speed. Heat is conducted across the boundary layer and then carried away by convection associated with free-air movement. The convection coefficient describing rates of heat flow through each layer is given by: \[\begin{equation} h_L=k \frac{V^{1/3}}{r^{2/3}} \tag{12.2} \end{equation}\] where \(V\) is the wind speed in cm/s, \(r\) is the radius of the layer in cm, and \(k\) is a constant describing thermal conductivity. The thermal conductivities of the fat (\(k_f\)), fleece (\(k_h\)), and air (\(k_a\)) additionally determine rates of heat exchange. (See further analysis below.)

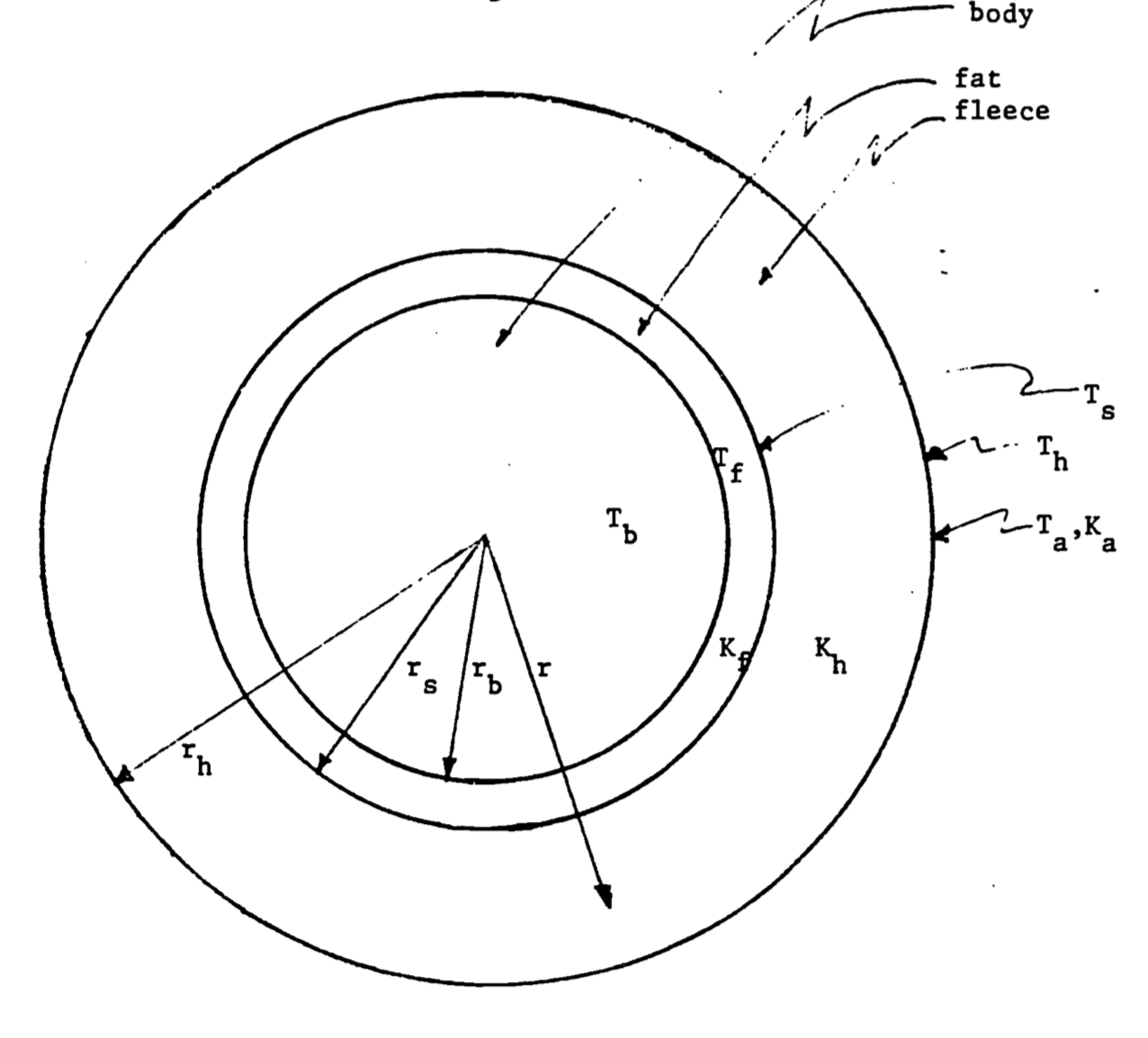
Figure 12.1: Sheep idealized as a cylinder. In the diagram, \(T_a\), \(T_b\), \(T_s\), \(T_h\) and \(T_f\) are the temperatures of the air, body, skin, hair tips and fat; \(r_b\), \(r_s\), and \(r_h\) are the corresponding radii of the cylinders; and \(K_a\), \(K_b\) and \(K_f\) are the thermal conductivities of air, fleece and fat.

At present, we will assume that \(T_b > T_h\), so that metabolic heat is lost to the environment, and will defer a discussion of the factors which combine to determine the surface temperature, \(T_h\), which is of paramount importance in our model.

The means by which metabolic energy is transported in the form of heat from the body to the fleece tips is conduction. It was observed by Fourier in 1822 that the rate of movement of heat \(Q(W)\) perpendicular to surface of area \(A\) through a material such as body fat or wool is proportional to the gradient of temperature \(T(K)\) in the material is: \[\begin{equation} Q=-kAdT/dr \tag{12.3} \end{equation}\]

Here \(k (W m^{-1} K^{-1})\) is a thermal conductivity coefficient, a property of the conducting material, and \(r (m)\) is the distance from the center of the cylinder measured along a radius.

Assuming a constant heat flow rate, integration of the expressions yields \[\begin{equation} Qr=-kAT + \mbox{const}. \tag{12.4} \end{equation}\] We can find the integration constant using \(T=T_b\) and \(d=0\) which gives \(\mbox{const}=kAT_b\).

Incorporating the constant in (12.4) gives \[\begin{equation} \frac{Qr}{kA}= T_b-T_r. \tag{12.5} \end{equation}\]

Here we can invoke the concept of thermal resistance (also referred to as thermal impedance), which is defined as the temperature variation produced by a unit heat flow rate: \[\begin{equation} Z= \frac{\Delta T}{r}. \tag{12.6} \end{equation}\]

Incorporating the concepts of resistance into (12.5) allows us to express resistance perpendicular to a surface area as \[\begin{equation} Z= \frac{r}{kA}. \tag{12.7} \end{equation}\]

Consultation with engineering texts indicates that the expression resistance corresponding to heat conduction through a hollow cylinder of internal radius \(r_i\) and external radius \(r_o\), length \(L\), and thermal conductivity \(k\) is \[\begin{equation} Z= \frac{1}{2\pi k_fL}ln(\frac{r_o}{r_i}). \tag{12.8} \end{equation}\]

We are now ready to use this expression to conduct an energy balance describing the internal heat conduction through layers of a sheep. We can define the resistances of fat layer as \[\begin{equation} Z_f=\frac{1}{2\pi k_fL}ln(\frac{r_s}{r_b}) \tag{12.9} \end{equation}\] and the fur layer as \[\begin{equation} Z_h=\frac{1}{2\pi k_hL}ln(\frac{r_h}{r_s}) \tag{12.10} \end{equation}\]

The temperature differences between the layers can then be expressed as the product of incoming heat and thermal resistances. The expressions for the fat and fur layers are thus as follows: \[\begin{equation} Z_f Q_f = T_b - T_s\\ Z_h Q_h = T_s - T_h \tag{12.11} \end{equation}\] where \(Q_f\) and \(Q_h\) are the quantities of heat reaching the outer surfaces of the fat and fur layers, respectively.

Analogous to electrical resistances, thermal resistance can be connected in series such that the expression for heat flow through the two layers is \[\begin{equation} Z_h Q_h + Z_f Q_f = (T_s - T_h) + (T_b - T_s) \tag{12.12} \end{equation}\]

Eliminating \(T_s\), we obtain \[\begin{equation} Z_h Q_h+Z_f Q_f=T_b-T_h \tag{12.13} \end{equation}\] At this point, it is important to point out that in general \(Q_h\) will not be equal to \(Q_f\). In the fat, rate of heat flow is exactly equal to that leaving the body, \[Q_f=M-E_r\] At the surface of the skin, however, heat is lost by sweating, so that \[Q_h=Q_f-E_s=M-E_r-E_s\] Substituting these results in (12.13), we obtain \[Z_h(M-E_r-E_s)+Z_f(M-E_r)=T_b-T_h\] or \[\begin{equation} M=E_r+\frac{E_s}{1+\frac{Z_f}{Z_h}}+\frac{T_b-T_h}{Z_h+Z_f} \tag{12.14} \end{equation}\] This important equation governs the rate of heat movement away from the animal’s body. Body heat produced by metabolism \(M\) is removed by evaporative losses due to respiration \(E_r\) and sweating \(E_s/(1 + Z_f/Z_h)\) and by conduction of sensible heat to the fleece tips \((T_b - T_h)/(Z_h + Z_f)\).