10.3 Animal Thermoregulation
The term thermoregulation can be defined as the ability of an organism to modify its body temperature. Although this may seem simplistic, the point is that a living organism often has a body temperature which would be different from that of an inanimate object with the same physical properties as the organism in the same thermal environment. For endothermic organisms, this fact is well known. The constancy of internal temperature of these animals helped Claude Bernard, a century ago, form his opinion that homeostasis is the central paradigm of physiology. But it was not until Heath’s (1964) paper that this point was clearly made for ectotherms. Huey (1974) studied the time and energy costs of regulating body temperature by contrasting body temperatures and spatial and temporal distributions of an iguanid lizard, Anolis cristatellis, in two different adjacent thermal environments: an open park and a forest. This ecological viewpoint is given a more general treatment by Huey and Slatkin (1976) in which they consider the costs and benefits of thermoregulation. Biologists have always recognized that the consequences of altering body temperature are profound. Today more emphasis is being placed on interpreting the importance of thermoregulation for circadian rhythms, circannual rhythms, foraging and digestive processes of individuals in their natural environment.
One can begin to understand the costs and benefits of temperature regulation by outlining the mechanisms that allow an organism to thermoregulate. In Table 10.1, these are placed under three convenient headings: behavioral, physiological, and morphological. This breakdown also chosen by King (1974) and West (1977) provides a starting point for discussion of alternative thermoregulation strategies. One might begin by determining the relative importance of each mechanism to heat transfer and its energetic cost to the organism. This kind of information is generally not known, but we will discuss one example later in the text which contrasts the effects of increasing body size and insulation thickness on heat loss.
What kinds of information are available from Table 10.1? First, the time scale on which each mechanism operates gives clues about the kind of environmental changes for which the mechanism has evolved to compensate. Second, the physical environment may dictate that certain mechanisms cannot be used. One obvious example is that of evaporative cooling in dry environments (Schmidt-Nielsen 1964). Here an organism must find other means to reduce its heat load because water is in short supply and is required for other purposes. A further complication is the interaction of several mechanisms. Consider the example of metabolic output as a function of air temperature given in most physiological texts. As the air temperature is lowered, the animal can maintain a thermal equilibrium by simply restricting blood flow to peripheral areas (vasoconstriction). This reduces the temperature in these areas (see Fig. 10.1). At the end of the thermal neutral zone when all the vessels are constricted (hot-cold dividing line in Fig. 10.2), the organism must increase its metabolic rate if its body temperature is to remain constant. In contrast, the blood vessels of an active animal must be dilated to supply the muscles with oxygen. Metabolic rate may increase by 300% or more to provide the energy for activity. Figure 10.3 shows resting and active metabolic rates for the rabbit Oryctolagus cuniculus as a function of temperature. When the rabbit is active, the metabolic rate is independent of air temperature. The challenge of physiological ecologists is to understand these mechanisms and their interactions for the animal in the natural environment.
TABLE 10.1. Systems or Mechanisms Influencing Thermoregulation in Animals.
| Behavioral | Time Scale of Adjustment |
|---|---|
| Habitat selection | S,L |
| Temporal selection of microhabitat | M,D |
| Spatial selection of microhabitat | M,D,S |
| Orientation | M |
| Body | |
| Body Appendages | |
| Caloric intake | D,S |
| Piloerection | M |
| Intraspecific grouping | M,S,L |
| Physiological | |
|---|---|
| Metabolic rate | M,S |
| Blood flow rate | M |
| Water loss | M |
| Respitory | |
| Panting | |
| Sweating | |
| Cutaneous | M |
| Color | S |
| Fat distribution | S |
| Fat melting point |
| Morphology | |
|---|---|
| Color | |
| Size | S |
| Shape | L |
| Surface characteristics | L |
| Fur | |
| Feathers | |
| Scales | |
| Circulatory system | L |
| Counter current exchange | L |
| Shunts | L |
M = Minute
D = Day
S = Season
L = Lifetime
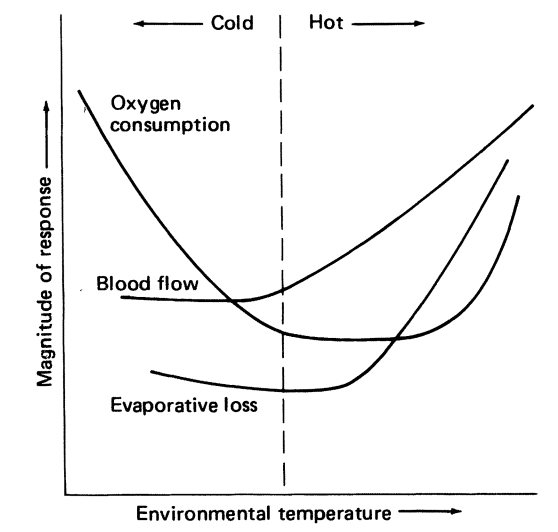
Figure 10.1: Oxygen consumption curve for a hypothetical homeotherm. The terms hot and cold can be defined in terms of the animal’s physiological responses to its environmental temperature. (From Ingram and Mount 1975, p.2,)
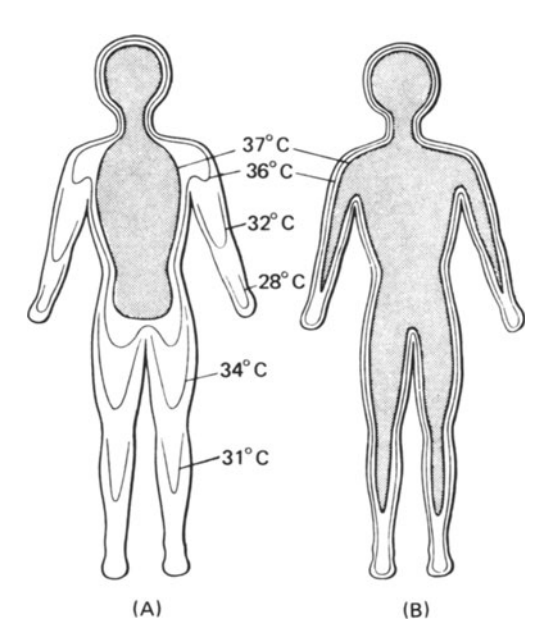
Figure 10.2: Diagrammatic isotherms in the human body exposed to cold (A) and warm (B) conditions. The core of deep body temperature (shaded) shrinks in the cold, leaving a peripheral shell of cooler tissue. (From Ingram and Mount 1975, p. 6: original data from Aschoff and Weyer 1958.)
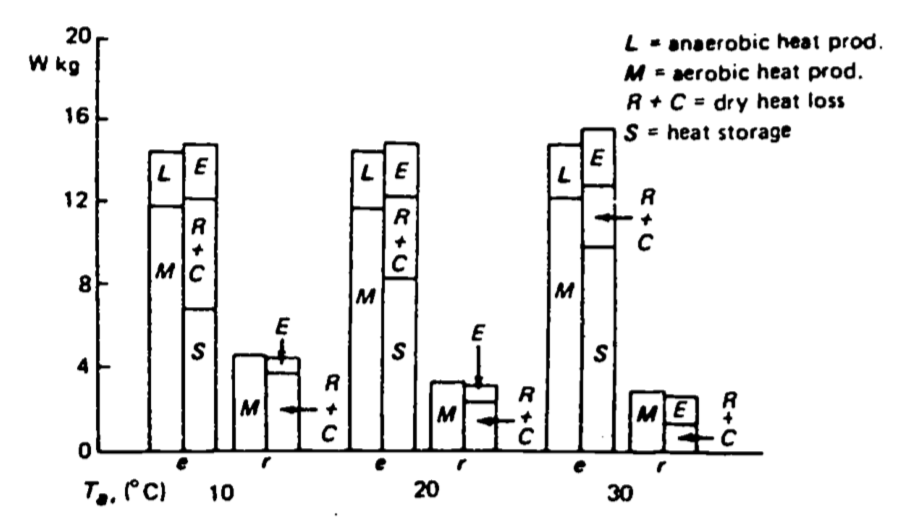
Figure 10.3: Mean heat production, loss and storage in three exercising (c) and four resting (r) New Zealand white rabbits at ambient temperatures of 10, 20 and 30°C. (From Kluger et al. 1972a.)
10.3.1 The Physical Environment
Another approach for studying thermoregulation is to examine the temporal and spatial variation of the thermal environment. This variation is a result of the patchiness and gradients of the physical factors in the heat energy equation: solar radiation, longwave radiation, wind speed, wind direction, air temperature, substrate temperature and water vapor concentration or water temperature. Vertical temperature gradients formed in the water, soil or air may allow an organism to locate in its preferred thermal environment. The increase in wind speed above the ground surface forms another kind of gradient. Patches usually created by sun and wind shadows are the result of the landscape and vegetation. If the patches are large compared to the size of the organism, then it may be necessary for the organism to move between patches to remain in thermal comfort. Hillman (1969) describes this behavior for the lizard Amevia leptophrys, which makes excursions into the forest habitat to forage but returns to the shrub community where sunlight is available to increase its body temperature. If patches are small, it may be possible for the animal to “sit” in two or more different thermal environments so as to balance its thermal energy exchange. If the patches become very small relative to the organism, the environment will appear homogeneous.
Another characteristic of the physical environment is that under certain conditions (e.g., clear or uniformly cloudy sky), the variability of thermal patches can be characterized quantitatively. Thus one can predict how the thermal environment will change in time and space. The work of Porter et al. (1973), who studied the desert iguana Dipsosauros dorsalis, is the best example of this modeling approach.
The reader should realize that the larger the variability in the micrometerological conditions the greater is the thermal stress the organism potentially experiences. In fact, most research has concentrated on adaptations to stressful environments. Physiologists have studied heat stress in deserts and cold stress in polar regions. This is the most likely course of investigation because the environments are harsh and the evolutionary solutions intriguing. Simple reasoning, however, suggests that a more complex viewpoint will have to be adopted for a complete understanding of animal thermoregulation in an ecological context.
Consider an arctic fox in the cold winter of the northern tundra. With a deep body or core temperature of about 38°C, it will be losing heat energy to the environment. Why is it that the fox does not increase its passive insulation (fur thickness) to conserve energy? One answer is that the animal would quickly overheat if its fur were too thick when it was exercising. This would have profound implications for the fox’s ability to capture prey. Bartholomew and Wilke (1956) and Brown and Lasewski (1972) provide examples relevant to this point.
Remember also it is probable that an animal can be too hot in the arctic winter and it may also become too cold in the tropics. It is likely that on any given day within any habitat an organism can experience either extreme. Thus the diversity of mechanisms found in Table 10.1 is not so surprising. Animals have a complex integrated approach for regulating their internal environment.
Finally note that an organism has two ways of dealing with thermal stress. It can tolerate the variability through physiological adaptations or it can avoid these climates or microclimates. The antelope ground squirrel Citellus leucurus, as most animals, employs both of these means. This desert mammal has evolved a large tolerance for body temperature fluctuations so that it can be active during the day under intense solar radiation. These conditions impose a net gain in heat energy and a corresponding rise in body temperature. To avoid thermal stress, the animal must retreat to its burrow where it can lose energy to the surrounding soil. Figure 10.4 shows the expected time course of its body temperature. When the body temperature drops, the animal has retreated to its burrow. We conclude that C. leucurus uses a combined strategy of tolerance and avoidance to be active on the sunlit desert surface.
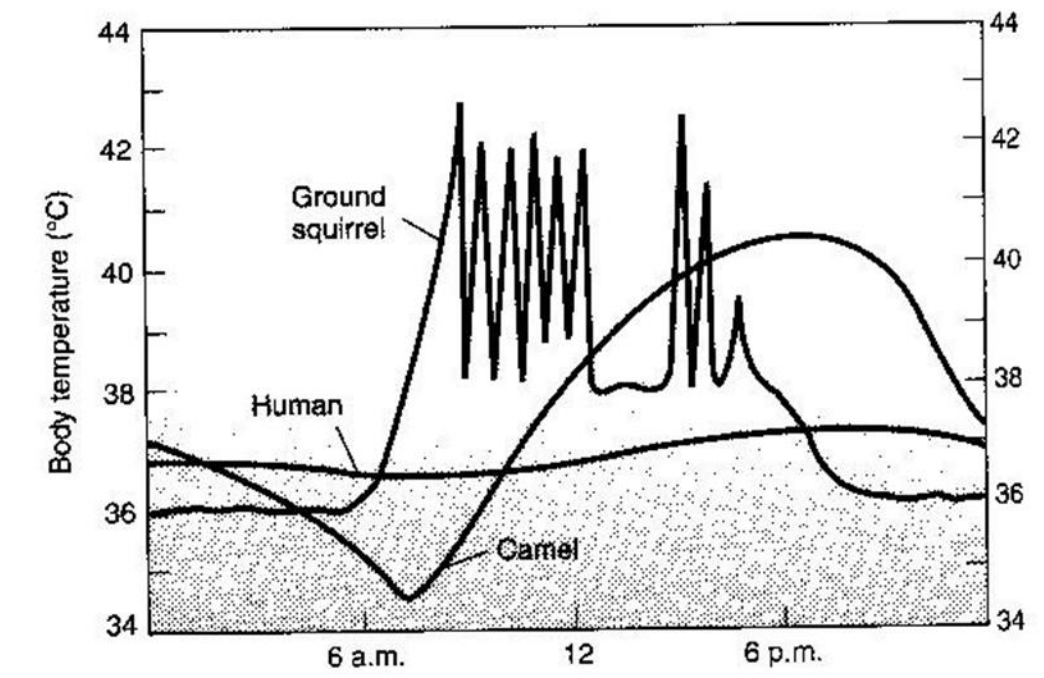
Figure 10.4: Diagrammatic representation of the daily patterns of body temperatures in a large and a small mammal subjected to heat stress under desert conditions. (From G.A. Bartholomew 1977, p. 423; original data from Schimdt-Nielsen et al., 1957, Amer. J. Physiol. 188: 103-112, and J.W. Hudson, 1962, Univ. Calif. (Berkeley and Los Angeles) Publ. Zool. 64:1-56.
10.3.2 Thermoregulation and the Ecogeographical Rules
During the course of their studies, early natural historians noted that there were clines in homeotherm size, shape and color. Three empirical ecological rules bearing the names of Bergmann, Allen and Gloger resulted from these observations. In addition, Cowles (1946) observed that there was a decrease in lizard body size at increasing latitudes. In each case, the originator proposed a reason why these observations might be true based on the animal’s thermal relation to the environment. The knowledge of energy balance and heat transfer processes explained in earlier modules (Stevenson 1977a,b, 1978a) will prove to be especially helpful in clarifying and dissecting each hypothesis.
Bergmann (1847) originally observed that, as the environment became colder, mammal and bird size increased. Although Mayr (1963, p. 323) has restricted Bergmann’s rule to variation within species, James’ (1970) translations indicate that Bergmann intended his rule to apply to larger taxonomic groups. To explain his generalization, Bergmann proposed that increasing body size would reduce heat loss. He reasoned that, since heat loss is proportional to surface area, metabolic output should be proportional to body mass to the 0.67 power. Increasing body size would therefore decrease the metabolic output per unit body weight.
There are several objections to this line of reasoning. First, modern measurements of standard metabolic rates of homeotherms have shown that resting metabolism is not proportional to the mass to the 0.67 power, but rather the 0.75 power. (Readers should consult McMahon (1973) for a suggestion of why this might be true.) Second, in a classical paper, in which they compared tropical and arctic birds and mammals, Scholander et al. (1950a) found that in most cases standard metabolism is independent of the environment. Challenging the physiological basis of Bergmann’s rule in a later paper, Scholander (1955) stated that there were three ways in which an organism could adapt to a colder climate: (1) by lowering the thermal gradient (decreasing body temperature), (2) by increasing metabolic rate or (3) by increasing body insulation. Based on earlier work (Scholander et al. 1950b,c), Scholander (1955) concluded that homeotherms increase fur and feather thickness to endure the colder climate of the arctic. This paper spurred a series of comments and rebuttals (Mayr 1956, Newman 1956, Irving 1957, Scholander 1956) which mainly serve to point out that there is a difference between the empirical observation and the reason for the “law.” As McNab (1971) correctly points out, a third objection is that increasing body size would reduce the heat loss per unit surface area, but in fact the total heat loss would increase as \({M_b}^{0.75}\). Increasing body size requires absolutely more energy. McNab concluded that much of the data used to support Bergmann’s rule could be interpreted as classical examples of character displacement (Brown and Wilson 1956). [See the field of metabolic ecology for recent research.]
These three arguments provide evidence to dismiss Bergmann’s reasoning. The empirical, basis of Bergmann’s rule, however, is still supported by more careful studies (James 1970, Brown and Lee 1969). The question now becomes “What selective forces would favor increasing body size in colder environments?”
Kendeigh (1969) made the plausible suggestion, for birds at least, that increasing body size will allow the animals to survive the critical times of severe weather when feeding is impossible. Developing this argument more formally, Calder (1974) states that during such conditions when the birds cannot forage, survival time depends on the amount of fat that is stored which is proportional to body mass. Because metabolism is proportional to \({M_b}^{0.75}\), a larger bird can survive a proportionately longer time. Retterson and Nolan (1976) discuss this hypothesis in relation to body size and the sex clines they found for the Dark-eyed Juncos, Juncos hyemalis hyemalis. The ecologist, however, is still left to explain McNab’s objection that a larger animal needs absolutely more energy. This might be rephrased as “Can a bird slightly larger than its conspecifics forage at a proportionately greater rate to meet its larger energy requirements?”
Spotila and Gates (1975) provide the only study that addresses Bergmann’s role and specifically incorporates the heat transfer processes. They conclude that indeed increasing body size will decrease the metabolic rate per unit surface area to achieve thermal equilibrium. Figure 10.5 clearly shows that size acts as insulation reducing the metabolic output. Given the alternative of increasing size or adding insulation, though, Figs. 10.5a and b show that a homeotherm (\(T=42^\circ{C}\)) and 2 cm in diameter in a cold environment can get the same reduction in metabolism by increasing insulation thickness 10 times instead of increasing body size to 10 cm in diameter. Their model only investigated the steady state situation. It would be instructive to incorporate temporal variations in the thermal environment.
In 1877, Allen wrote that species from colder climates often have smaller appendages than do closely related species in warmer climates. He suggested that this was an adaptation to conserve heat in cold environments. Mayr (1963) states that Rensch (1933) made quantitative measurements which upheld Allen’s rule. The problem is that decreasing surface area decreases the rate at which an organism can absorb energy as well as release energy. If the environment is always colder than the organism, it should assume a spherical shape and avoid the plate shape. As already noted earlier in the text, at times it may be important to increase heat loss even in the coldest environment. By reducing surface area, the organism has less ability to direct blood flow to influence its, heat balance physiologically, but an increase in the surface area to volume ratio may require more energy to keep surface tissue from freezing. The effects of natural selection on such trade-offs are not clear.
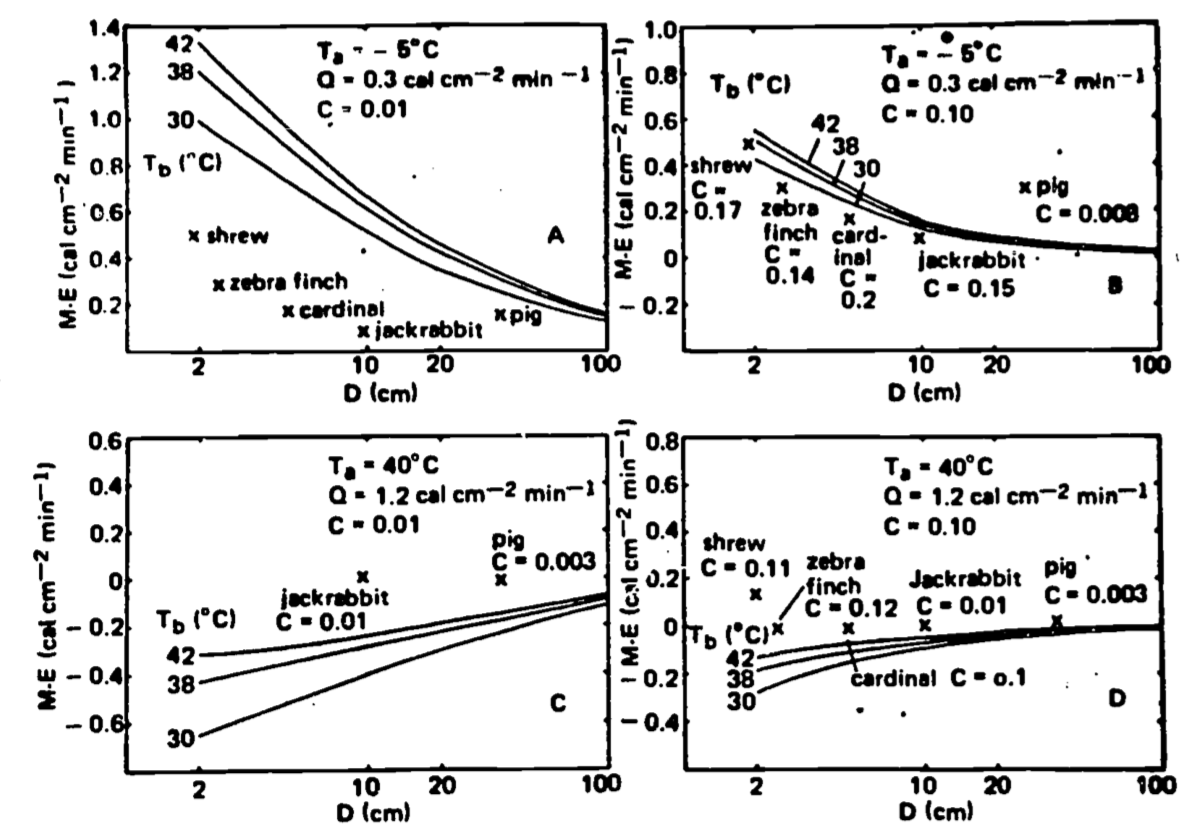
Figure 10.5: Effect of body size and insulation on the M-E requirement of homeotherms. (A) Cold conditions, clear sky at night, low insulation. (B) Cold conditions, clear sky at night, increased insulation. (C) Full sun, high air temperature, low insulation. (D) Full sun, high air temperature, increased insulation. Insulation consists of a layer of fur or feathers, the thickness of the layer defined as CD, where D is the inside diameter with no insulation and C is a constant proportion of D for all sizes of D in a given set. Data for real animals are taken from Porter and Gates (1969). (From Spotila and Gates 1975, p. 295.)
There are several well-documented examples of the importance of appendages in thermoregulation. Farlow et al. (1976) investigated the sail fin of the dinosaur Stegosaurus. Studies of the vascular system and a model of heat transfer implicate the dorsal fin as an important heat transfer mechanism. The pinna of Leporidae (hares and rabbits) is a favorite topic of vertebrate physiologists (Kluger et al. 1971, Hill and Veght 1976, Schmidt-Nielsen et al. 1965, Wathen et al. 1971). These investigators have shown that the large surface area (20% of the body) of the external ear is a useful mechanism to control heat exchange. Their large surface area, which improves convective and radiation exchange, combined with the ability to pump blood through the tissue makes an effective regulation system. Wathen et al. (1971) have made wind tunnel and theoretical investigations exploring various geometries. Hesse (1928) and Griffing (1974) provide empirical evidence for Allen’s rule. But there are no theoretical studies comparable to the work of Spotila and Gates (1975) to help interpret this phenomenon.
Gloger (1833) postulated that lighter colored animals are found in more open habitats because they emitted more radiation. From modern physics, however, we know that color is not important in determining emissivity to longwave radiation. Almost all organisms have emissivities above 0.5 (Monteith 1973). Hock (1965) pointed this out and ascribed the importance of color to camouflage. In his investigation of animal color, Hamilton (1972) distinguishes three categories: communication, camouflage (from predators and from prey) and radiation exchange. He correctly states that color will be important for absorption of solar radiation. Hamilton (1972) believes that open habitat birds often have the problem of overheating in the daytime. In this environment, coloration will reflect solar radiation thus reducing the heat load. Since these habitats also tend to be cooler at night, these birds should have thicker plumage to conserve heat after dark. Hamilton presents some comparative and physiological data which supports his hypothesis. Omhart and Lasiewski (1970) and Lustick (1969) have made O2 consumption measurements below the thermal neutral zone showing that black-colored birds have reduced metabolic requirements compared to white birds. If the reader understands radiation transfer, this result is not so surprising. In fact, the reduction in metabolic rate can be accurately predicted as shown later in the module.
The heat transfer processes in the fur and feathers are just beginning to be explored (Davis and Birkeback 1974, Cena and Monteith 1975a, b,c). Physically, as light penetrates the pelage or plumage, it gets reflected forward and backward creating concave temperature distributions. Kowalski (1978) has found the radiation and conduction processes are coupled in the heat transfer. In general, a white-colored outer layer will absorb less radiation, but as wind speed increases, Walsberg et al. (1979) found that the reduction in absorbed radiation for black feathers was larger. This is because the maximum temperature in the plumage layer was closer to the surface in the black than in the white feathered skin. Therefore convection will have a larger effect on the black-colored bird. Further studies will be able to investigate fur and feather characteristics (thickness, length, density) which eventually can be incorporated into a model of the total animal in the environment to understand the interactions of wind speed and radiation on absorbed radiation.
In 1946, Cowles suggested that lizard size should decrease with increasing latitude because increasing size would decrease the rate at which a reptile could achieve activity temperature. This hypothesis has never been rigorously tested. Ray (1960) and Lindsay (1966) examined latitudinal trends in size changes for a variety of invertebrate species but reached no conclusions.
Most models of thermoregulation have started with certain assumptions about the morphology and physiology of the organism and then attempted to ask about the control of body temperature (Huey and Slatkin 1976) or the limit of activity times (Belovsky 1977; Porter et al. 1973, Porter and Tracy 1975) and habitat (Tracy 1976). Other characteristics such as body shape and size, surface characteristics (scales, hair, feathers), preferred body temperatures, basal metabolic rate, and the design of the circulatory system also merit our attention since they too are under selective pressures. For instance, a question of interest for many years has been the evolution of homeothermy (Cowles 1946, Ricgles 1974, Whittow 1973, Heath 1968, Bakken 1971, Bakken and Gates 1975, Heinrich 1977, McNab 1978, Stevens 1973, Dawson 1975, Bouvier 1977, Calloway 1976, Crompton et al. 1978, Hainsworth and Wolf 1978). The question of preferred body temperature obviously has implications for the biochemical system of the organism which is also being investigated (Brock 1967, Hochaka and Somero 1973, Somero and Low 1975). [See Angilletta (2009, Thermal Adaptation) for recent treatments of the issues in the preceeding paragraphs.]
10.3.3 Other Ecological Considerations
Because of its very existence, every organism exchanges heat energy with its environment, it is natural to ask about the relation of thermoregulation to the tasks an individual must perform which include growth, procurement of food, avoidance of predation and reproduction. Although these are standard subjects for ecological studies, their relation to thermoregulation is largely unexplored. Several paragraphs on the interaction of feeding and temperature regulation are included to spur the reader’s interest.
It seems quite natural that the ecologists studying thermoregulation should become interested in the food requirement of their subjects. The chemical energy obtained is used for basal metabolism as well as all other tasks the animal must perform. In turn, the metabolic rate is a significant component of the heat energy balance of homeotherms, while for poikilotherms the thermal environment will influence the animal’s body temperature and thus its metabolic rate.
What about ecologists interested in predicting an animal’s food items? Investigators modeling feeding strategies (although not specifically concerned with thermoregulation costs) have provided some insight into temporal patterns and foraging modes (see Pyke et al. 1977 and Norberg 1977). Schoener (1974) states that an organism should forage during a given period if the energetic gain is greater than resting during that period. Symbolically this is stated: The animal shall forage if \[\begin{equation} e_x > {-W}_x \tag{10.1} \end{equation}\] where- \(e_x\) is the net energy gained while feeding in a period of type \(x\)
- \(W_x\) is the energy lost while waiting through a period of type \(x\)
He summarizes:
These considerations imply that temporal specialization should vary with food abundance in exactly the opposite manner to food or habitat specialization. In situations of very high food abundance, only the best item kind is taken and only the best patch type is foraged in. Hence specialization on food type and habitat is at its maximum. But under situations of greatest food abundance, there should be no time during which feeding results in a greater loss of energy than waiting. Hence temporal specialization is at its minimum. With decreasing food abundance, item kinds and habitat types are added, but it is possible that food availability becomes so low during certain periods of time that it is less expensive to wait those periods out. Hence food and habitat type broaden while diet activity periods shrink as abundance decreases.
... Of course it is possible that animals will not be as generalized with respect to time as contingency models imply, if by being so generalized they gain more food than they can process. Such animals, or any animal with a fixed caloric requirement should specialize with respect to time as food abundance increases, just as they should for food or habitat. Thus contingency feeders and restricted feeders should react in opposite ways to changes in overall food abundance. Williams (10) reports that during poor weather when yield from the best feeding periods is less, certain animals (daddy-longlegs, cattle) enlarge their activity times.Such animals are behaving as if they have a fixed caloric quota.
- \(F_x\) is energy captured (\(W\)),
- \(M_{fx}\) is metabolism foraging (\(W\)),
- and \(M_{rx}\) is metabolism while resting (\(W\)).
If the costs of the two environments are much different or the probability of finding food is low, it may be that an organism should skip foraging periods more often. Consideration of the daily and seasonal foraging patterns of organisms suggests the question: “Why do animals spend so much of their time waiting or resting?” Katz (1974) developed a long-term foraging optimization scheme to investigate some of these issues. Brett (1971) provides some intriguing data on the interaction of food levels and temperature.
The remainder of this module returns to questions of heat balance. The ecologist, however, must constantly keep this broader perspective in mind if he or she is to investigate the patterns found in nature.