1.12 Solution to the Additional Problems
- First partial derivatives: \[\begin{align*} \frac{\partial E^2}{\partial A} &= \int^{30}_3\frac{\partial}{\partial A}(6.1(x+5.0)e^{-0.045x}-Ax-B)^2dx \\ &= 2 \int^{30}_3(6.1(x+5.0)e^{-0.045x}-Ax-B)(-x)dx \end{align*}\] Equating to zero and dividing by 2 gives \[0 = -\int^{30}_36.1(x-2+5x)e^{-0.045x}dx +\int^{30}_3Ax^2+Bxdx\] Successive integration by parts (for the first integral) and direct integration (for the second integral) yield the first equation: \[0 = 8991.0A + 445.5B - 25984.9\] \[\begin{align*} \frac{\partial E^2}{\partial B} &= \int^{30}_3\frac{\partial}{\partial B}(6.1(x+5.0)e^{-0.045x}-Ax-B)^2dx \\ &= -2 \int^{30}_3(6.1(x+5.0)e^{-0.045x}-Ax-B)dx \end{align*}\]
Equating to zero, dividing by 2 and solving yields the second equation: \[0 = 445.5A + 27.0B - 1568.8\]
The solutions are \(A= 0.061\), \(B = 57.1\). The least squares integral using the approximation \(Y = 0.061x + 57.1\) is 546.452.
- Let \(x=a\sin\theta\). The limits of integration are then changed as follows \[-a \le x \le a\] \[ -a \le a\sin\theta \le a\] \[ -1 \le \sin\theta \le 1\]
There are many options for the range of \(\theta\). We first change the integrand to see which range is suitable. We know the integrand is non-negative since \(x^2 \le a^2\). Substitution gives
\[x = a\sin\theta\]
\[dx = a\cos\theta\:d\theta\]
\[\sqrt{a^2-x^2}dx = \sqrt{a^2 - a^2\sin^2\theta}\cdot a\cos\theta \:d\theta\]
The integrand is then non-negative when the positive square root is used and when \(\cos \theta\) is non-negative. Thus, we choose the limits of integration to be \(-\frac{\pi}{2}\), \(\frac{\pi}{2}\) since \(\sin(-\frac{\pi}{2}) = 1, \sin(\frac{\pi}{2}=1)\) and \(\cos\theta \le0\) if \(-\frac{\pi}{2} \le \theta \le \frac{\pi}{2}\).
The integral is then
\[\int^{\pi/2}_{-\pi/2}\sqrt{a^2-a^2\sin^2\theta}a\cos\theta \:d\theta = a^2\int^{\pi/2}_{-\pi/2}\sqrt{1-\sin^2\theta}\cos\theta\:d\theta\]
\[\begin{align*}
&= a^2\int^{\pi/2}_{-\pi/2}\cos^2\theta\:d\theta=a^2[\frac{\theta}{2}+\frac{\sin2\theta}{4}]^{\pi/2}_{-\pi/2} \\
&= a^2[\pi/4+(1/4)(0)-(-\pi/4)-(1/4)(0)] =\pi a^2/2
\end{align*}\]
Thus
\[A=\frac{2b}{a}\int^a_{-a}\sqrt{a^2-x^2}dx = \pi ab\]
When \(a = b = 5.57\), \(A = 97.47\).
When \(a = 5\), \(b = 6.09\), \(A = 95.66\).
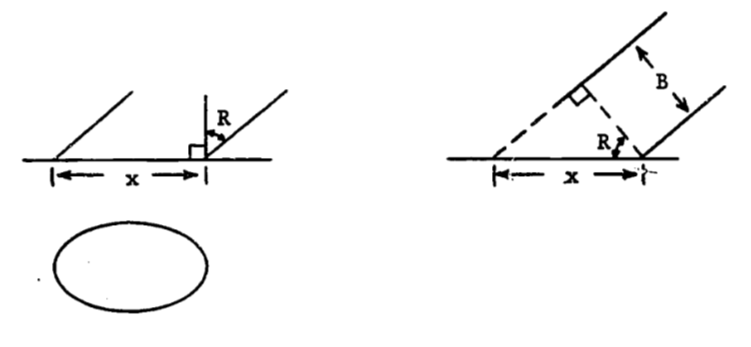
From the right-hand diagram, we have \[\cos R = B/x\] and thus \[x=B/\cos R\] The minor axis is then the circle’s diameter, \(B\). In the answer to part “a”, we replace \(2a\) by \(B/\cos R\) and \(2b\) by \(B\).
\[\begin{align*} A &= \pi ab = \pi(B/2\cos R)(B/2) \\ &= \pi B^2 / (4 \cos R) \end{align*}\]
Since the area of the circle is \(\pi B^2/4\),the dilution coefficient is
\[D = \frac{\pi B^2/4}{\pi B^2/4\cos R} = \cos R\]
Thus \(D=0.6\) means less dilution than \(D=0.3\), and \(D=1.0\) means no dilution at all. For Minnesota, the coefficients are
\(D=0.94\) for \(R=20°\)
\(D=0.42\) for \(R=65°\)