10.7 Problem Set
Pick an animal and discuss what factors in Table 10.1 will be most important in its thermoregulation strategy. Include in your response any factors that have been omitted from the table.
When an endothermic animal is resting, there can be a range of standard operative environmental temperatures within which its heat production or metabolic rate is constant. This thermal neutral zone, as it is called, is shown in Figs. 10.1, 10.6 and 10.8. What mechanisms does an animal have available to maintain constant core temperature and heat production when the thermal environment is changing? Discuss the relative importance of each.
Using the information in Fig. 10.3, what are the avenues of heat gain and heat loss for an exercising rabbit?
At different temperatures, some terms are constant while others are changing. Why? Identify the factors which may have caused the end of the exercise period. Is there a temperature at which one of these factors is likely to be more important?
Appendages serve a variety of functions but all are included under Allen’s rule. Contrast the foot of a seagull with its wing with regard to the importance of each for heat balance when the animal is resting and exercising. (You may choose your own organism and set of appendages.) Support your discussion with knowledge about other functions of the appendages. Any physiological or behavioral information will strengthen your conclusions.
You are researching the prospects of entering the aquaculture business raising sockeye salmon (Oncorhynchus nerka). In the graph below juvenile sockeye growth is given as a function of food and temperature conditions. What is the temperature for maximum growth rate when food rations are at 6, 4.5, 3.0 and 1.5% of dry body weight per day. Fish food is relatively cheap and you could afford to provide maximum rations, but the average water temperature in the pond you plan to use is only 7°C so that the fish are not achieving maximum growth rates. Discuss the conditions in which it would be economically advantageous for you to raise the water temperature. How high would you raise it? What might be the ecological consequences of heating the water for the rest of the aquatic community.
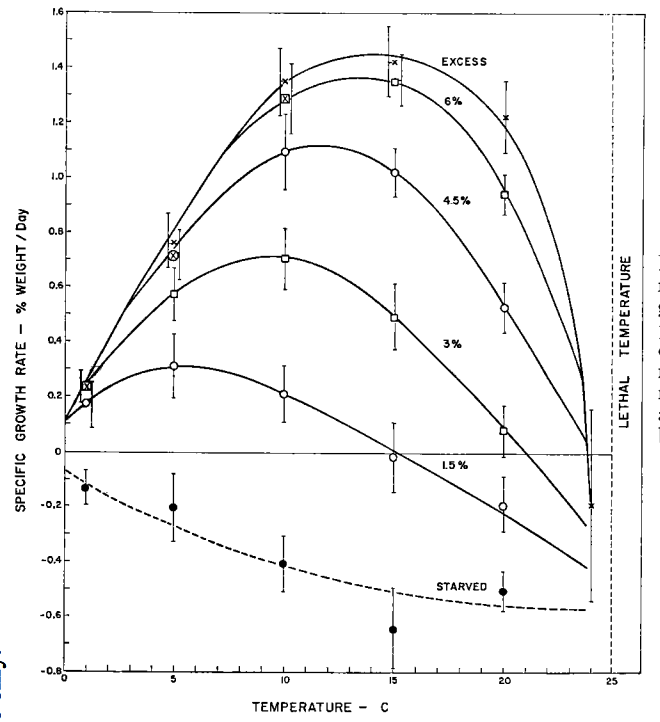
Figure 10.11: Effect of reduced ration on the relation betwern growth rate (±2 SE) and temperature, for 7 to 12 month-old sockeye. Points for excess ration or where a prescribed ration turned out to be excessive are marked with an X. The broken line for starved fish is a provisional interpretation (From Brett,J.R. et al.1969, p. 2381.).
- Imagine that you are studying the foraging and activity patterns of the Ortax, a large ungulate, and a carnivorous beetle, the Diplitz. You have divided the day into ten equal time periods and measured \(F_x\), \(M_{fx}\), and \(M_r\) for each period as shown in the table below.
| Time Period | Ortax | Diplitz | ||||
|---|---|---|---|---|---|---|
| \(F_x\) | \(M_{fx}\) | \(M_{rx}\) | \(F_x\) | \(M_{fx}\) | \(M_{rx}\) | |
| 1 | 6 | 3 | 2 | 20 | 10 | 1 |
| 2 | 6 | 5 | 2 | 25 | 10 | 2 |
| 3 | 7 | 7 | 3 | 8 | 10 | 2 |
| 4 | 7 | 2 | 3 | 4 | 10 | 2 |
| 5 | 7 | 2 | 2 | 2 | 10 | 2 |
| 6 | 7 | 2 | 1 | 0 | 9 | 2 |
| 7 | 8 | 1 | 1 | 1 | 9 | 1 |
| 8 | 6 | 2 | 2 | 2 | 8 | 1 |
| 9 | 6 | 4 | 2 | 7 | 7 | 1 |
| 10 | 6 | 2 | 1 | 14 | 8 | 1 |
Rank the time periods in order of decreasing net caloric profit, assuming the animals can choose between resting and foraging. Are there any time periods the animals should be resting instead of feeding? If both organisms are trying to gather energy stores, what pattern of feeding activity would you expect to see using this simple model? What is the most each can expect to “make” during one cycle? If the Ortax must make a net profit of 20 caloric units per day to prepare for winter when should it feed to minimize total feeding time? If it must maintain weight how should it feed? If both animals must wait one time period to digest its food after it has a full stomach of 22 units, what is its feeding schedule to maximize net profit? Remember to consider \(F_x\) values to figure digestion limits. Assume the Ortax must skip two periods. How should it feed to maximize profit?
You work as a biologist for the consulting company Envirotech. The firm’s latest contract calls for an evaluation of the potential impact on the quail populations of a logging plan in Americana National Forest. Describe how you would fulfill this contract. Specifically, discuss the importance of food and cover on population densities and individual health.
Using the theory derived in the module and the data below, calculate \(T_b\) for the three cases given. What is the environmental and the physiological contribution to \(T_b\) in each case? What two kinds of animals are represented?
| \(M\) | \(E_r\) | \(E_b\) | \(Q_a\) | \(K\) | \(T_a\) | \(M_b\) | |
|---|---|---|---|---|---|---|---|
| Animal | (W m-2) | (W m-2) | (W m-2) | (W m-2) | (W m-2 °C-1) | (°C) | (kg) |
| 1 | 20 | – | 10 | 550 | 180 | 15 | 0.07 |
| 2 | 150 | 25 | 100 | 750 | 15 | 20 | 0.008 |
| 3 | 45 | – | 40 | 850 | 200 | 25 | 0.01 |
Assume \(\varepsilon = 0.95\), \(V = 0.25 m s^{-1}\), \(\overline{T}_r = 25^\circ C\),\(h_c = 17.24V^{0.60}M_b^{-0.133}\).
Using the data in problem 8 for the two ectotherms, calculate \(K_0\) for V = 0.1, 0.5, and 3.0 m s\(^{-1}\). Assume that the difference between metabolism and water loss is zero. What is \(T_b\) in each case now? If the heat capacity is equal to the specific heat (3430 J kg\(^{-1}\) °C\(^{-1}\) ) times the mass of the animal, what is the heat capacity for each? Assuming \(Q_a = 600 W m^{-2}\)and \(T_a = 20^\circ C\) for the range of wind speeds above which animal will get warmer. Are your conclusions still the same if \(Q_a = 380 W m^{-2}\)? Integrate equation (10.10) to find \(T_b\) as a function of time. If the initial body temperature of both animals is 10°C at time equal to zero, which animal will get to \(T_b = 25^\circ C\) first? Use the following relationship from Mitchell (1976).
\[\mbox{Area}=11.0\times\bigg(\frac{\mbox{body mass}}{\mbox{body density}}\bigg)^{2/3}\] where body density equals \(1\times10^3 kg m^{-3}\) to correct the dimensions of the equations. What is the difference in time between when each will arrive at 25°C? (Hint: Solve the integrated equation for time.) Answer the preceding two questions for V=0.1 and 0.5 m s-1. Assume the animals are lizards and comment on Cowles’ suggestion.Include a conduction term of the form \(G(T_r-T_g)\) in equation (10.2) and find an equation analogous to equation (10.5) for \(T_b\).
Imagine you are employed as an entomologist with the U.S.D.A. working with a team of research scientists studying a pest that drills into the stalks of corn. Your assignment is to investigate the importance of the physical environment in the corn-insect interaction. Ten years of historical data suggest that during cold springs the corn is not badly infected. Also it is known that chemical treatments are most effective on the third instar. These specific questions are important to managing this pest.
Will this be a high density year for the corn drill so that biological or chemical controls will be needed?
If so, when during the season will most of the insects be in this instar? Discuss your research plan to address these questions.