11.11 Answers to the Problem Set

1.Transpiration increases with windspeed for lines 1 and 2, i.e., \(r_l\) = 168 s m^-1 but decreases with wind speed for lines 3 or 4.

par(mar = c(5, 5, 3, 5))
fig.vr=sapply( seq(0,600,100), FUN=est_TlTrans, T_a=40, rh=0.5, 
               V=0.1, D=0.001, W=0.02, Q_a=800)
plot(fig.vr[1,], fig.vr[2,], type="l", col='tomato', 
     xlab="Leaf temperature (°C)", 
     ylab= expression("Leaf transpiration (kg / " * m^2 * "s)"), 
     xlim=range(35,45), ylim=range(0.0,0.001))
fig.vr=sapply( seq(0,600,100), FUN=est_TlTrans, T_a=40, rh=0.5, 
               V=2.1, D=0.001, W=0.02, Q_a=800)
points(fig.vr[1,], fig.vr[2,], type="l", col='tomato2')
fig.vr=sapply( seq(0,600,100), FUN=est_TlTrans, T_a=40, rh=0.5, 
               V=4.1, D=0.001, W=0.02, Q_a=800)
points(fig.vr[1,], fig.vr[2,], type="l", col='tomato3')
fig.vr=sapply( seq(0,600,100), FUN=est_TlTrans, T_a=40, rh=0.5, 
               V=6.1, D=0.001, W=0.02, Q_a=800)
points(fig.vr[1,], fig.vr[2,], type="l", col='tomato4')

fig.vr=sapply( seq(0.1,6.1,0.2), FUN=est_TlTrans, T_a=40, rh=0.5, 
               r_l=0, D=0.001, W=0.02, Q_a=800)
points(fig.vr[1,], fig.vr[2,], type="l", col='skyblue', 
       lty="dashed")
fig.vr=sapply( seq(0.1,6.1,0.2), FUN=est_TlTrans, T_a=40, rh=0.5, 
               r_l=200, D=0.001, W=0.02, Q_a=800)
points(fig.vr[1,], fig.vr[2,], type="l", col='skyblue2', 
       lty="dashed")
fig.vr=sapply( seq(0.1,6.1,0.2), FUN=est_TlTrans, T_a=40, rh=0.5, 
               r_l=400, D=0.001, W=0.02, Q_a=800)
points(fig.vr[1,], fig.vr[2,], type="l", col='skyblue3', 
       lty="dashed")
fig.vr=sapply( seq(0.1,6.1,0.2), FUN=est_TlTrans, T_a=40, rh=0.5, 
               r_l=600, D=0.001, W=0.02, Q_a=800)
points(fig.vr[1,], fig.vr[2,], type="l", col='skyblue4', 
       lty="dashed")

legend("top", c("V=0.1", "V=2.1","V=4.1","V=6.1"), lty=c(1), 
       bty = "n", col = c('tomato','tomato2','tomato3','tomato4'))
legend("topright", c("r_l=0", "r_l=200", "r_l=400", "r_l=600"), 
       col = c('skyblue','skyblue2','skyblue3','skyblue4'), 
       lty='dashed', bty = "n")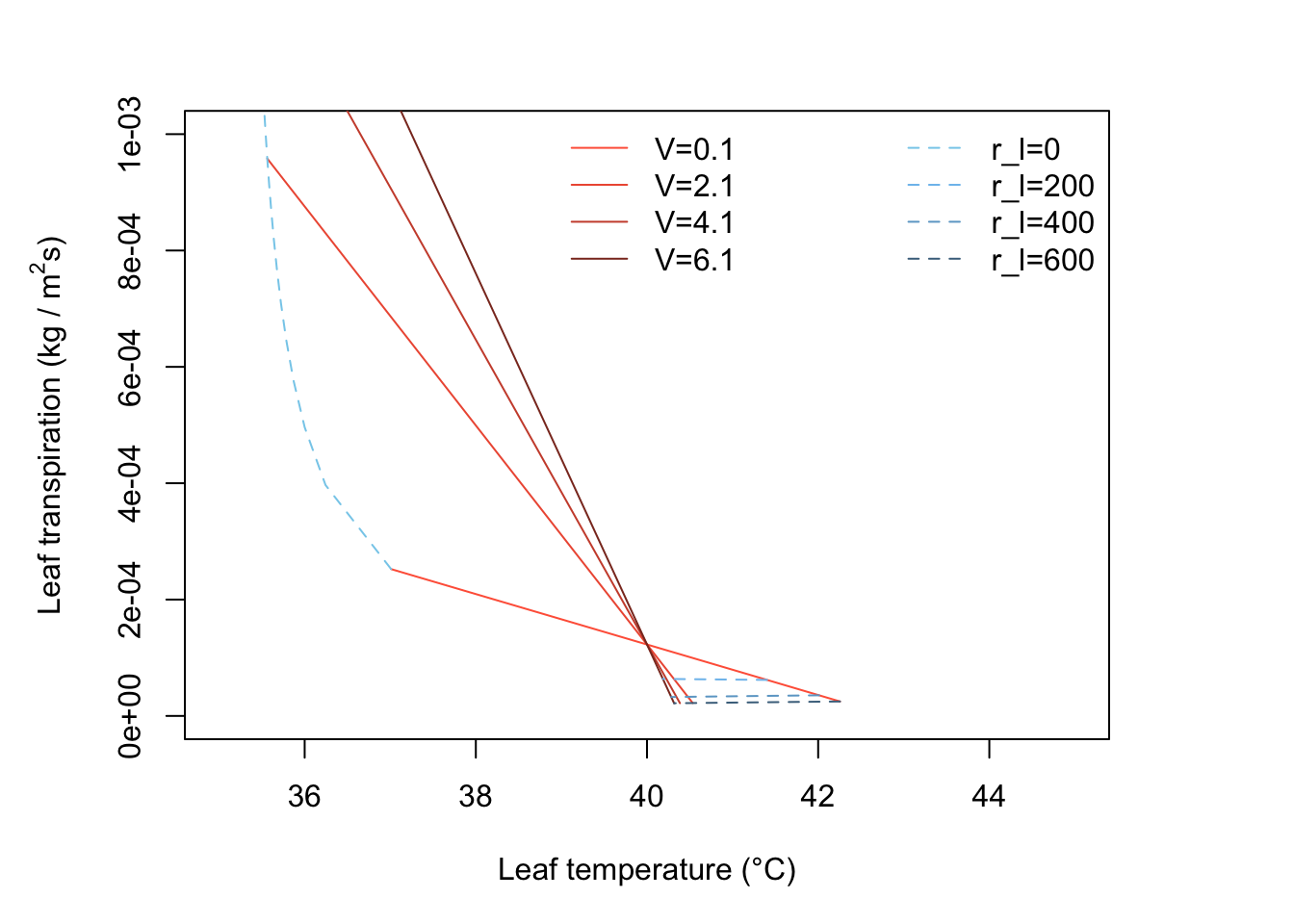

2. The leaves will be long and thin so that their dimension in the direction of the wind is always small. They must be less than about 0.015m wide, and are essentially unlimited in length.

par(mar = c(5, 5, 3, 5))
fig.vr=sapply( seq(0.01,0.1,0.005), FUN=est_TlTrans, T_a=35, 
               rh=0.2, V=0.1, W=1, Q_a=800, r_l=2000) #1045.6
plot(fig.vr[1,], fig.vr[2,], type="p", 
     xlab="Leaf temperature (°C)", 
     ylab= expression("Leaf transpiration (kg / " * m^2 * "s)"))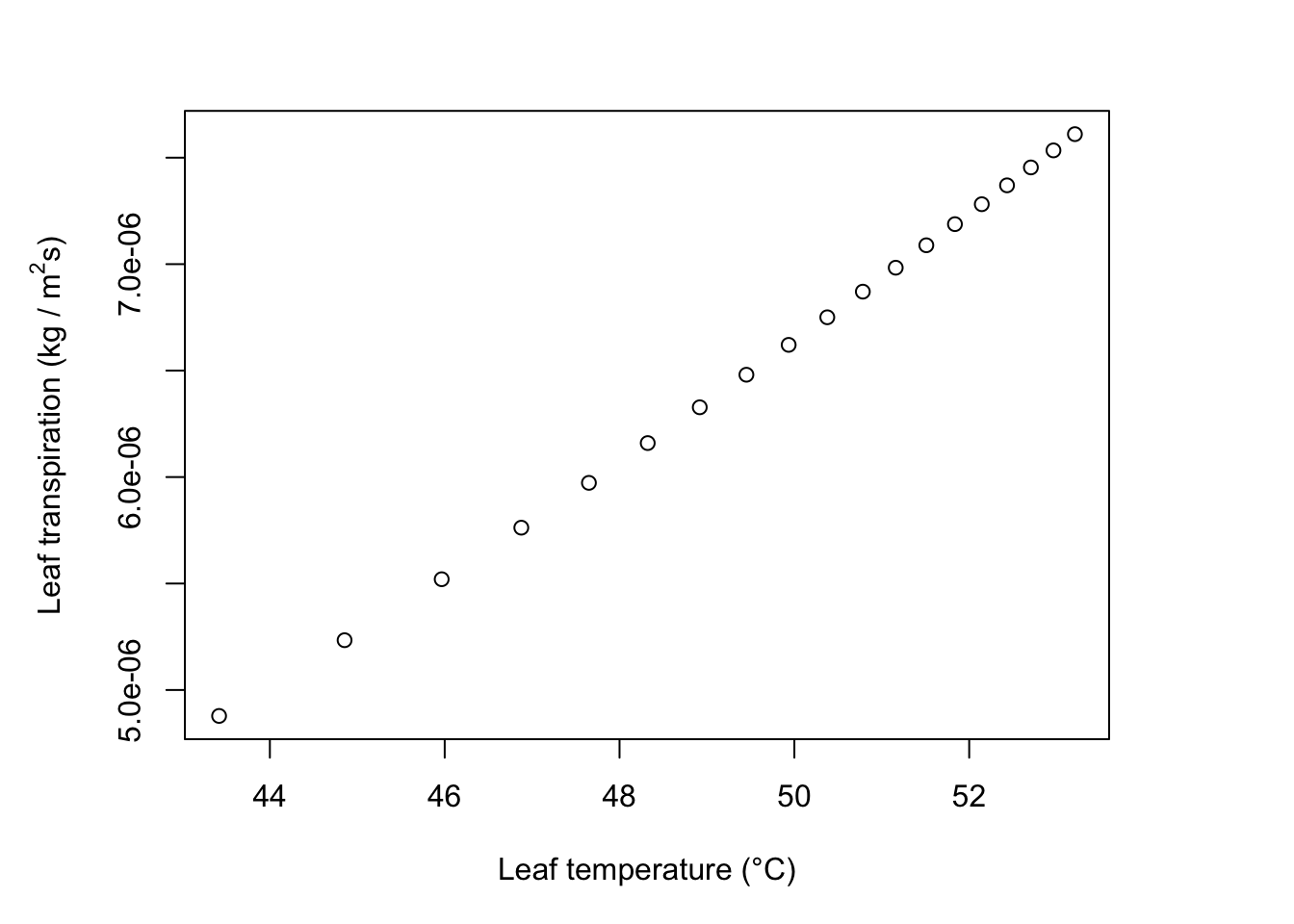

3. We estimate the heat dissipation components as follows:

#a)
#fig 3
par(mar = c(5, 5, 3, 5))
fig.vr=sapply( seq(0,600,100), FUN=est_TlTrans, T_a=40, rh=0.2, 
               V=0.1, D=0.05, W=0.05, Q_a=800)
plot(fig.vr[1,], fig.vr[2,], type="l", 
     xlab="Leaf temperature (°C)", 
     ylab= expression("Leaf transpiration (kg / " * m^2 * "s)"))
fig.vr=sapply( seq(0.1,6.1,0.2), FUN=est_TlTrans, T_a=40, rh=0.2, 
               r_l=200, D=0.05, W=0.05, Q_a=800)
points(fig.vr[1,], fig.vr[2,], type="l", lty="dashed")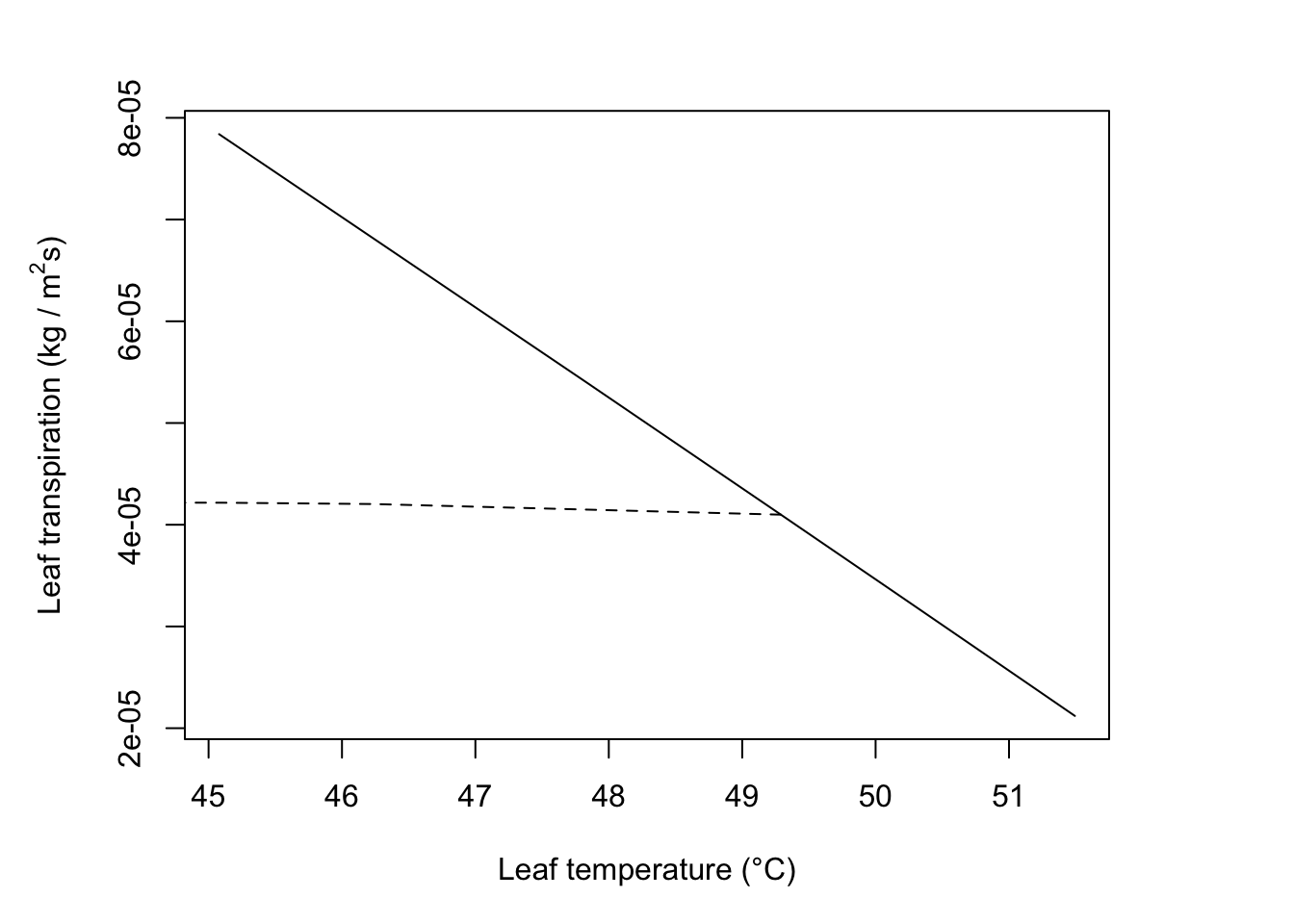

#Calculate components
T_a=40; rh=0.2; V=0.1; D=0.05; W=0.05; Q_a=800; r_l=200
T_l= 49.3
#reradiation
epsilon *sigma*(T_l + 273)^4

## [1] 587.348

#convection
k1*(V/D)^0.5*(T_l-T_a)

## [1] 120.211

#latent heat transfer
L*(vd(T_l, rh)-rh*vd(T_a, rh)) / 
  (r_l + k2*(D^{0.3}*W^{0.20})/ V^{0.50})

## [1] 92.68941

#b)
#fig 3
fig.vr=sapply( seq(0,600,100), FUN=est_TlTrans, T_a=40, rh=0.2, 
               V=2.1, D=0.05, W=0.05, Q_a=800)
plot(fig.vr[1,], fig.vr[2,], type="l", 
     xlab="Leaf temperature (°C)", 
     ylab= expression("Leaf transpiration (kg / " * m^2 * "s)"))
fig.vr=sapply( seq(0.1,6.1,0.2), FUN=est_TlTrans, T_a=40, rh=0.2, 
               r_l=0, D=0.05, W=0.05, Q_a=800)
points(fig.vr[1,], fig.vr[2,], type="l", lty="dashed")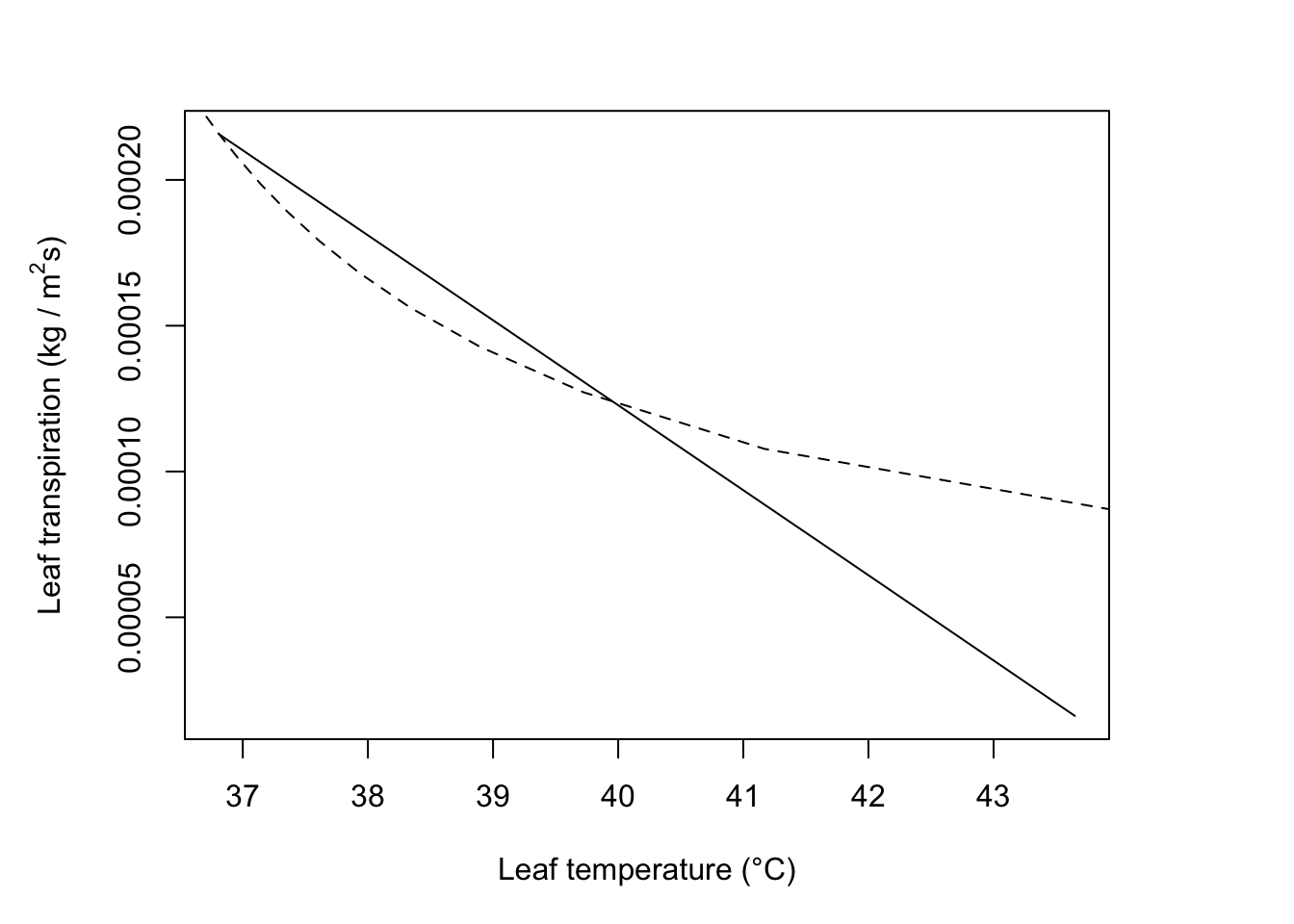

#Calculate components
T_a=40; rh=0.2; V=2.1; D=0.05; W=0.05; Q_a=800; r_l=0
T_l= 40
#reradiation
epsilon *sigma*(T_l + 273)^4

## [1] 522.4343

#convection
k1*(V/D)^0.5*(T_l-T_a)

## [1] 0

#latent heat transfer
L*(vd(T_l, rh)-rh*vd(T_a, rh)) /
  (r_l + k2*(D^{0.3}*W^{0.20})/ V^{0.50})

## [1] 599.3688

#c)
#fig 8
fig.vr=sapply( seq(10,40,10), FUN=est_TlTrans, r_l=500, rh=0.8, 
               V=0.1, D=0.05, W=0.05, Q_a=700)
plot(fig.vr[1,], fig.vr[2,], type="l", xlim=range(20,50),
     ylim=range(0.0,0.0001), xlab="Leaf temperature (°C)", 
     ylab= expression("Leaf transpiration (kg / " * m^2 * "s)"))
fig.vr=sapply(seq(0,1000,100), FUN=est_TlTrans, T_a=10, rh=0.8, 
               V=0.1, D=0.05, W=0.05, Q_a=700)
points(fig.vr[1,], fig.vr[2,], type="l", lty="dashed")

#Calculate components
T_a=10; r_l=500; rh=0.8; V=0.1; D=0.05; W=0.05; Q_a=700
T_l= 26
#reradiation
epsilon *sigma*(T_l + 273)^4

## [1] 435.0499

#convection
k1*(V/D)^0.5*(T_l-T_a)

## [1] 206.8146

#latent heat transfer
L*(vd(T_l, rh)-rh*vd(T_a, rh)) / 
  (r_l + k2*(D^{0.3}*W^{0.20})/ V^{0.50})

## [1] 47.53626