14.9 Answers to the Problem Set

  1. \[\begin{align*} Re&=\frac{\bar{u}d}{v} \\ &=\frac{(10 m s^{-1})(3m)}{1.5\times10^{-5}m^2s^{-1}}=\frac{30}{1.5\times10^{-5}}=2\times10^6 \end{align*}\] For \(v=0.1ms^{-1}\), \(Re=2\times10^4\)

  2. Solve the second equation for \(z\): \[z=4x-2\] Substitute this expression into the first equation: \[x+2y+3(4x-2)=10\] or \[13x+2y=16\] As was probably obvious from the outset, no solution is possible without some further information about either \(x\), \(y\) or \(z\); i.e., we need a third equation. This is an illustration of the so-called closure problem in turbulence which occurs with the Reynolds equations. In simple terms, this problem is “solved” by adding a third empirical equation; one derived from observations, not theory. Thus, if it is observed that usually \(x=-2\), then we may solve the system of equations: \(y=21\), \(z=-10\). Of course, our final answer is in general only as good as the validity of our assumption that \(x=-2\) for any given case.

Re 3000 6000
\(\bar{u}\) 1.6 cm s-1 3.2 cm s-1
\(d\) 0.8 mm 1.0 mm
\(u'/\bar{u}\) 0.0242 0.0229
\(T\) 50 ms 33 ms

Two things are of importance to note. First of all, since \(Re\) is proportional to velocity, and from the problem statement it is fair to assume fluid viscosity, density and flow geometry have stayed the same. It is safe to surmise that \(\overline{u}\) doubled when \(Re\) was increased from 3000 to 6000. Secondly, while \(d\) increased with \(Re\), which tends to oppose mixing, \(T\) decreases in larger proportion. In a similar line of argument to that of the text, we may argue that \(T\) gives an indication of the life span of the average eddy of size \(d\). Over a time equivalent to several time scales, an eddy can be expected to have become completely mixed with other eddies. Thus, apparently the decrease in \(T\) more than makes up for the increase in \(d\), so that mixing becomes more efficient as \(Re\) gets larger.

  1. Equation (14.10) is \(u_*=kz\frac{d\bar u }{dz}\)
    rearranging terms \(\frac{k}{u_*}d\bar u =\frac{dz}{z}\)
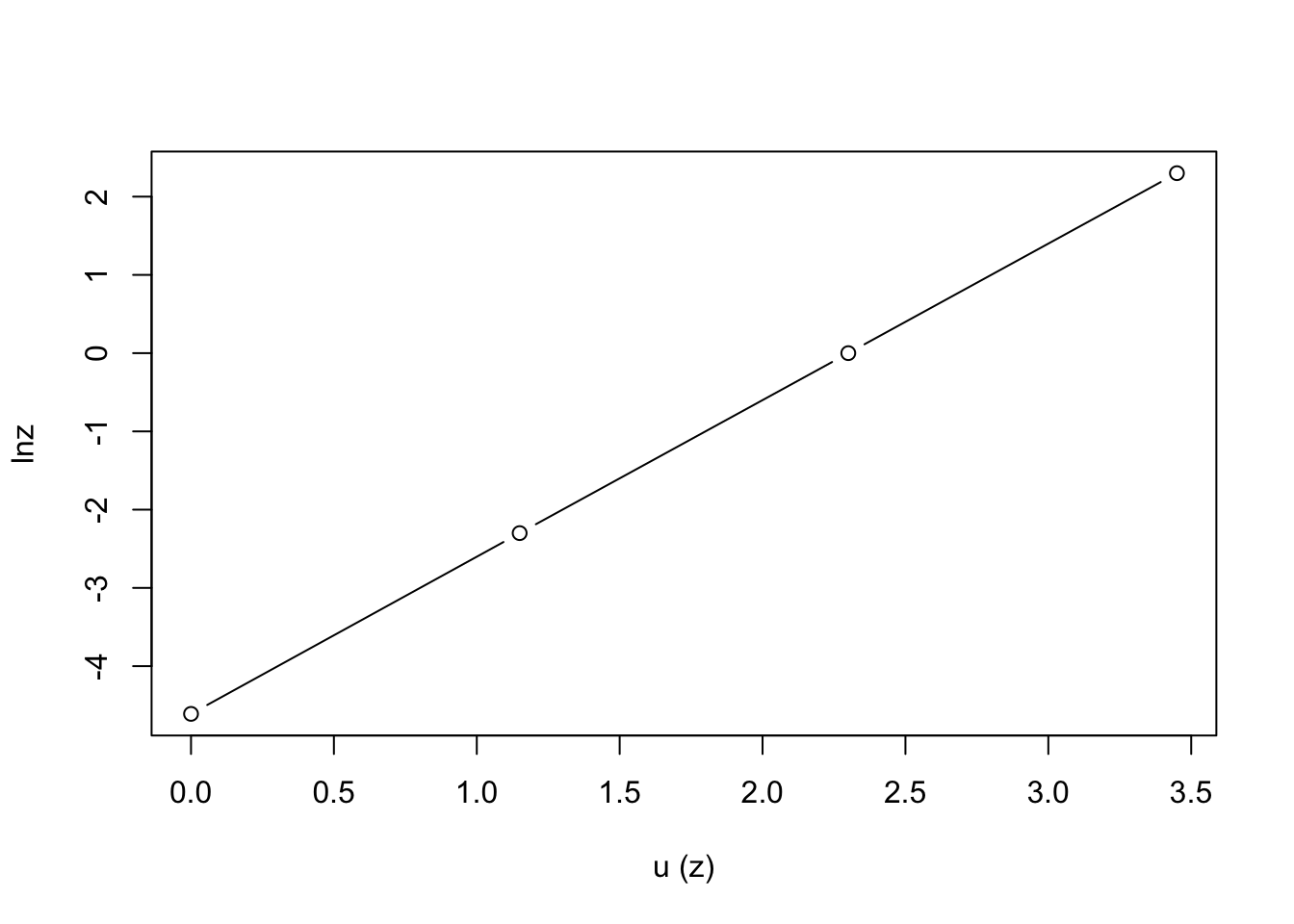
    integrating \(\frac{k}{u_*} \int_0^{\bar u} d \bar u=\int_0^z\frac{dz}{z}\) \[\frac{k\bar u}{u_*}=\ln z-\ln0\] But, \(\ln 0\) is infinite, so we introduce a small constant called the surface roughness (\(z_0\)), and integrate from \(z=z_0\) to \(z=z\). Thus, we are saying that the velocity is zero a small distance (\(z_0\)) above the surface \[\frac{k\bar u }{u_*}=\ln z-\ln z_0=\ln\left(\frac{z}{z_0}\right)\]
\(z\) \(\ln z\) \(\overline u(z)= 1/2 \ln(z/0.01)\)
\(z_0=0.01\) \(\ln z_0= -4.61\) 0
0.1 -2.3 1.15
1 0 2.30
10 2.3 3.45 
u= c(0,1.15,2.30,3.45)
lnz= c(-4.61,-2.3, 0, 2.3)
plot(u, lnz, type="b", xlab="u (z)")

  1. \[\begin{align*} Re&=\frac{ud}{v}=\frac{3ms^{-1}\times0.042m}{151\times10^{-7}m^2s^{-1}}=8.3\times10^3 \\ Nu&=ARe^n=0.6Re^{0.5}=55 \\ F_H&=55\times\frac{26mWm^{-1}°C^{-1}}{0.042m}(30-20)°C \\ &=339000\frac{mW}{m^2}=339\frac{W}{m^2} \end{align*}\]