4.4 Gravitational Force

The story of gravitation begins with the ancients observing the motions of the planets among the stars, and eventually concluding that they went around the sun, a fact much later picked up by Copernicus. Tycho Brahe had the revolutionary idea (at least by comparison to the ancients) that one could measure the movements of the planets and establish their paths in space, which then might resolve the arguments as to whether they indeed moved around the sun. Tycho made extensive measurements, which Kepler then used to establish his three famous laws: (1) planets move in ellipses, with the sun at one focus, (2) the radius vector from sun to planet sweeps out equal areas in equal times, and (3) the period of revolution about the sun is proportional to the 3/2 power of the semimajor axis of its orbit.

Galileo also studied the laws of motion, coming up with the principle of inertia (that undisturbed bodies coast forever in a straight line), which Newton extended by introducing the notion of force, which it was necessary to apply in order to either speed up or slow down the body, or perhaps to cause it to deviate from a straight line path.

In the process of his theoretical studies on the motion of planets, Newton invented the calculus, from which he was able to show that Kepler’s second law on equal areas being swept out in equal times followed from the assumption that the forces on the planets were directed exactly toward the sun. Furthermore, Kepler’s third law was found to require that the force diminish with distance from the sun, in fact that the force had to be inversely proportional to the square of the distance from the sun. Finally, Newton proposed that the phenomenon of gravitation was universal, that everything attracts everything else, and used this with his inverse square law to demonstrate that the planets must move in accordance with Kepler’s first law, in ellipses about the sun, as must any smaller body (such as a moon) about its parent body (say a planet).

Newton’s law of universal gravitation is: \[\begin{equation} F=G\frac{m_1m_2}{r^2} \tag{4.2} \end{equation}\]

where
    \(F\) = force of one body on the other (newtons)
    \(m_1,m_2\) = masses of the two bodies (kilograms)
    \(r\) = distance between the two bodies (meters)
    \(G\) = gravitational constant = 6.670 \(\times\) 10^-11 nt m²/kg²

This force is the weakest of the four known basic force laws. We tend only to notice its existence when at least one of the masses is very large, such as the earth is, and often don’t realize that all masses attract each other gravitationally (which, of course, is why it’s known as a “universal” law). At the molecular level, gravity plays an insignificant role in life processes (where electrical forces, which are about 10⁴⁰ times as powerful as gravity, are the most important). However, on a macroscopic scale, gravity plays an important role in determining structure and function of organisms, and ultimately limits the size of large animals (with the result that the largest of earth’s creatures are aquatic, where the buoyant force of water opposes the force of gravity; and which dictates, in general, that aquatic creatures have lower energy requirements than terrestrial forms).

The weakness of gravity makes the determination of \(G\) tricky. Cavendish was the first to successfully measure \(G\) in the laboratory, which he did with an apparatus called a torsion balance. It consists of a horizontal arm suspended by a thin torsion fiber. Lead balls on each end of the arm are gravitationally attracted to a pair of large stationary lead balls, which applies a twist to the fiber in proportion to the force.

4.4.1 Electromagnetic Force

The classical theory of electromagnetism as it was ultimately developed in the 19th century, and which culminated in Maxwell’s synthesis of the laws of electricity and magnetism with those laws of the behavior of light, is one of great beauty and also of great complexity. It is too complicated to present here in entirely correct detail, but though the formulas we give are approximations, they will suffice for our purposes of understanding something of life systems.

As students of cellophane laundry bags have observed in dry weather, there seems to be an entirely different sort of force from gravity, one which is strongly attractive between the bag and the hairs of one’s forearm. More diligent students have experimented with hard rubber rods and cat’s fur, glass rods and silk, and have discovered that there must be two different kinds of matter, which we call “positive” and “negative,” such that two “positives” or two “negatives” repel each other, while “positive” and “negative” matter will attract one another. We say hard rubber becomes negatively charged when rubbed with cat’s fur, and glass becomes positively charged when rubbed with silk. We now know that electrical charge is a property of the constituents of the atom, positive electricity defined to be associated with the nuclear proton, and negative electricity associated with the orbital electron. Furthermore, the charge on the rubber and glass rod gets there by transferring electrons from the cat’s to the rubber, and from the glass rod to the silk.

In 1785, Coulomb discovered with the use of a torsion balance that, like gravity, the force between charged bodies varies inversely as the square of the distance between them. Nowadays, Coulomb’s electrostatic force law is written: \[\begin{equation} F=\frac{1}{4\pi\varepsilon_o}\frac{q_1q_2}{r^2} \tag{4.3} \end{equation}\] where
    \(F\) = force (newtons)
    \(r\) = distance between charges (meters)
    \(q_1,q_2\) = charge on bodies 1 and 2 (coulombs)
    \(\frac{1}{4\pi \varepsilon_o}\) = 8.987 \(\times\) 10⁹ \(\frac{nt\cdot m^2}{coul^2}\)

The unit of charge, the coulomb, is formally defined today in terms of the amount of silver deposited on an electrical terminal under a certain electrical current, but for the purposes of this module it will be easier to define the coulomb in such a way that the magnitude of the charge \((e)\) on an electron (which is exactly the same in magnitude as the charge on a proton) is given by:

\[e=1.6019\times10^{-19}coul\] The coulomb is one of the five fundamental units (length, time, mass, electrical charge, and temperature) in terms of which all physical units may be expressed. The constant of proportionality (\(\frac{1}{4\pi\varepsilon_o}\)) is arbitrarily assigned this strange form by physicists so that certain other of their expressions derived from Coulomb’s law are more aesthetic in appearance than they otherwise would be.

As the above problems illustrate, the magnitude of the electrostatic force is enormous. Yet in our everyday experience the balance between negatively and positively charged matter (electrons and protons) is so nearly perfect in most objects that we fail to notice it. In fact, if you were standing at arm’s length from someone, and each of you had one percent more electrons than protons, the repulsive force between you would be sufficient to lift a weight equal to that of the earth (Feynman 1963).

Despite the near-perfect macroscopic balance of electrons and protons, if a small volume of matter is viewed at the atomic scale, electrons and protons are not present in equal numbers and do not balance out over the volume. Thus there are strong residual electrical forces which give the neutral atom its integrity and which account for the rigidity and strength of most solid materials.

Under the strong attractive force between them, electrons and protons try to get as close to each other as they can, up to a certain limit. To understand why they don’t get closer to each other than they do (~10^-8 cm) requires a knowledge of quantum mechanics beyond the scope of this set of modules. Suffice it to say that if the electron were confined in a region too close to the nuclear protons, Heisenberg’s uncertainty principle would require the electron to possess a large momentum which would effectively keep it out of the nucleus (most of the time!).

But what holds the protons together in such close proximity in the nucleus? The repulsive electrostatic force between two or more protons is just huge at sub-nuclear distances (~10^-13cm). The answer is that there is another basic force which keeps the nucleus together, and which must be attractive and more powerful than the electrostatic force. This is called the strong nuclear force, which along with another weaker-than-electrostatic force called the weak nuclear force, comprises the third and fourth basic force laws and completes the description of all the basic force laws known to physicists today. We shall not discuss these last two laws further, other than to say that they are not “inverse square” laws, but rather act only over very short distances. The strong nuclear force is not appreciable in magnitude beyond distances roughly equal to the diameter of a uranium nucleus. In fact, the uranium nucleus with its 92 protons and its approximately 145 neutrons, is on the verge of flying apart under electrostatic repulsion. A small nudge, as might be given it by smacking into a low energy neutron, will cause it to fly apart (fission) and release the electrical energy (commonly, but erroneously, called “nuclear energy”) stored in the close proton-to-proton affiliation.

We have described the law of interaction between charges at rest. To complete our description of electrical forces in this module, we must set down the law by which forces act between charges in motion. This is the phenomenon of magnetism, which when coupled with the law for electrostatics (and in fact we know now from the special theory of relativity that they are inseparable) forms the basis for what we term electromagnetic phenomena. The description of the magnetic force is difficult without introducing the intermediary concept of a magnetic field (it’s difficult enough even this way!). It goes like this: (1) a moving charge sets up what we call a magnetic field; (2) another charge in motion experiences a force as it moves through this magnetic field.

The Biot-Savart law (sometimes called Ampere’s law) describes the magnetic field set up at a distance \(r\) from moving charges (current) in a wire (see Fig. 4.4): \[\begin{equation} dB=\frac{\mu_o\;i\;dl\;\sin\theta}{4\pi r^4} \tag{4.4} \end{equation}\] where
    \(dB\) = incremental magnetic field (weber/m²)
    \(i\) = electric current (coul/s \(\equiv\) ampere)
    \(dl\) = incremental length of current carrying wire (m)
    \(r\) = distance from \(dl\) to point where \(dB\) is measured (m)
    \(\theta\) = angle between \(dl\) and \(r\)
    \(\frac{\mu_o}{4\pi}\) = 10^-7 weber/amp-m

The units for magnetic field \((B)\) will be seen from Equation (4.5) (next page) to be nt-sec per coul-m, which is conventionally called weber/m² instead.

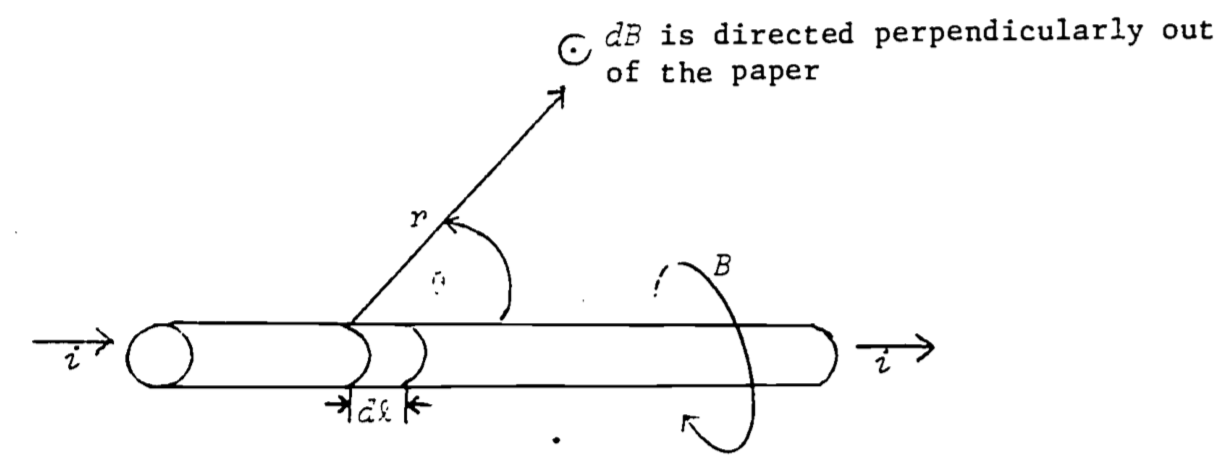
Figure 4.4: Magnetic field produced by current-carrying wire (Biot-Savart)

If the thumb of your right hand is pointed in the direction of the current, the magnetic field circles about the wire in the direction of the fingers of your right hand.

The force on a charge \((q)\) moving through a magnetic field \((B)\) is given by:

\[\begin{equation} F=qvB\sin\Psi \tag{4.5} \end{equation}\]

where
    \(F\) = force (nt)
    \(q\) = charge (coul)
    \(v\) = velocity of charge (m/s)
    \(B\) = magnetic field (weber/m²)
    \(\Psi\) = angle between velocity vector and \(B\) (as \(v\) rotates into \(B\)).
The direction of the force is as shown in Fig. 4.5.

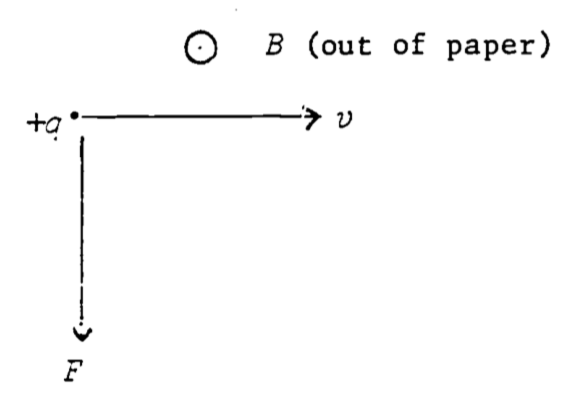
Figure 4.5: Force on charge moving through constant magnetic field.

In other words, if the fingers of the right hand follow \(v\) as it rotates into \(B\), the thumb points in the direction of the force (true for positive charge–negative charge changes the sign of the force vector).

It is worth noting that all of what is now known as classical electromagnetic theory was summarized by Maxwell into four compactly written vector differential equations (beyond the scope of these modules!), cleverly called Maxwell’s equations, which when solved by Maxwell led him to the following conclusion:

If two charges are initially held a distance \(r\) from each other, and at time 0 one of the charges is made to jiggle up and down with a frequency \(f\), the second charge will eventually experience a force on it which changes at the same frequency \(f\) with which the distance between the two charges is varying. But it will not experience this changing force immediately at time 0! The news that the first charge has started to jiggle does not arrive until \(\frac{r}{v}\) seconds after the jiggling has begun, where \(v\) is the velocity at which the news travels, and which was predicted by Maxwell’s equations to be:

\[v=\frac{1}{\sqrt{\mu_o\varepsilon_o}}=\sqrt{8.987\times10^9\times10^7}=2.998\times10^8m/s\] \[=c=\;\mbox{velocity of light}\] Note that \(\varepsilon_0\) and \(\mu_0\) were measured in the laboratory under static conditions as the proportionality constants in Coulomb’s and Biot-Savart’s laws, respectively. This seemingly remarkable coincidence, that electromagnetic radiation travels at the same speed at which light had been previously found to travel, led Maxwell to the inevitable conclusion that light was an electromagnetic phenomenon, which of course has been borne out. We now know that the light which we see is caused by the frantic jiggling of electrons, the color we see depending on the frequency of the jiggling. The electromagnetic spectrum extends far beyond the ability of our eyes to see however, ranging (in practical terms) from the very low frequency waves used in long-distance radio communication, through the higher frequency television and radar waves, through the infra-red (heat), visible, and ultraviolet, to X-ray and \(\gamma\)-ray frequencies. The study of the interaction of electromagnetic radiation of different frequencies with matter, its absorption, transmission, and reflection as dependent on the chemical make-up of the matter and the frequency of the radiation, has long occupied the physicist and is of central importance to the proper design of a living organism, plant or animal, enabling it not only to cope with its thermal environment but to sense the presence of its food or its enemies. Other modules also discuss this interaction and its importance in greater detail.

In conclusion, the electromagnetic forces are by far the most important of any of the basic force laws in understanding the living organism. Atomic processes, whether they be the “physical” processes involved in changes of state…solid, gas, or liquid…or the “chemical” processes involved in exchanges of partners between atoms, are basically manifestations of the electromagnetic force laws (sometimes necessarily being modified by the rules of quantum physics). Certain other processes, such as elastic collisions between molecules or between large objects, hence friction, are really the result of an electrostatic repulsion between molecules at close range. In short, most of biophysics and biochemistry could ultimately be explainable (in theory, at least!) by an elaborate application of Maxwell’s classical laws and those of modern quantum electrodynamics.

4.4.2 Other Force “Laws”

Friction, Intermolecular Forces, Hooke’s Law

There are other so-called force laws which are usually treated in elementary presentations, which, though apparently having a reality of their own, are seen on closer inspection to be consequences of the basic laws of electromagnetism. For example, the frictional “drag” force on a body moving through a fluid (liquid or gaseous) is observed to be proportional to the velocity of the body relative to the fluid if the velocity is slow enough that no turbulence is present. At higher velocities, the force opposing the motion may be more nearly proportional to the square of the velocity. This is the case when an airplane flies through the atmosphere at subsonic speed. The frictional force “law” is actually a consequence of the molecules of the fluid bombarding the object, changing their momentum during the act of collision, which is in turn a consequence of the strong repulsive electrostatic force between two molecules as they approach too closely. The sum of the basic electromagnetic interactions between a myriad of molecules results in the measured drag forces in a manner so complicated that the frictional effects have never been calculated from first principles.

The force between two molecules requires a knowledge of quantum mechanics for a full understanding; nonetheless a good qualitative understanding of such forces can be couched in classical terms. It is necessary to consider cases, since many molecules have fundamental asymmetries, such that the mean positions of their negative and positive charges do not coincide. The water molecule serves as an example, where the negative charge tends to reside more on the oxygen, creating what we call a dipole. Thus there are strong attractive forces between water molecules in a dipole-dipole interaction.

Even in molecules where the mean positive and negative charges coincide (non-polar molecules), such as is true in oxygen gas, the positive and negative charges do have some limited freedom to rearrange themselves, and this will happen in the presence of a nearby molecule. Since like charges repel and unlike charges attract, the charges rearrange themselves in such a way that the respective distances between like charges are slightly greater than the distances between unlike charges. The net repulsive force is therefore less (the like charges are farther apart) than the net attractive force (unlikes are closer together) and the molecules attract one another. Such a rearrangement is illustrated in Fig. 4.6. It is known from the principles of quantum mechanics that non-polar molecules are attracted at long distances by a force which is inversely proportional to the seventh power of the distance, that is, \(F = \frac{k}{r^7}\). However, when the molecules get too close they repel one another with great force. These results are summarized in Fig. 4.7.

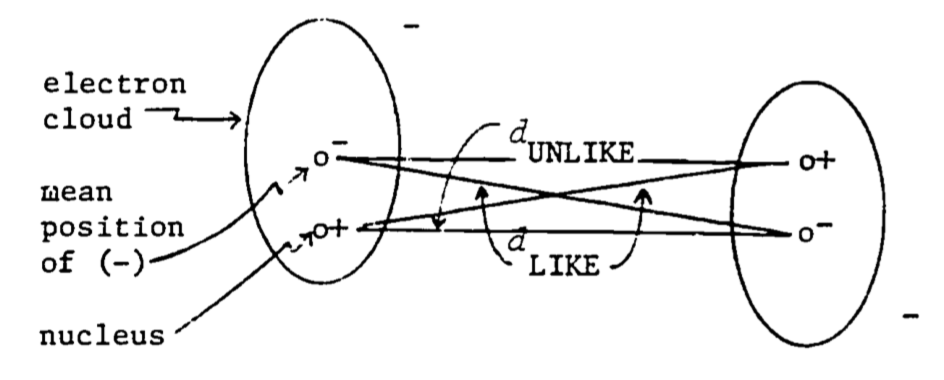
Figure 4.6: Induced dipole-dipole interaction in otherwise non-polar molecules.

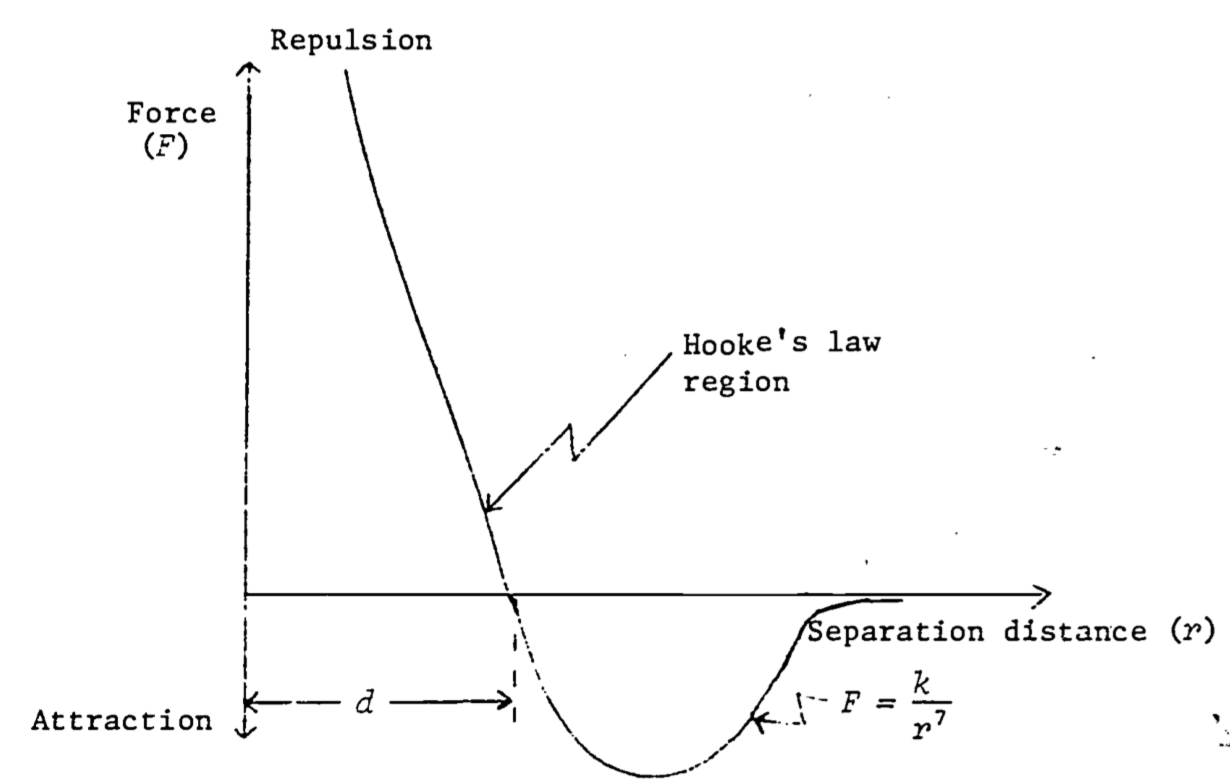
Figure 4.7: Force between two non-polar molecules as a function of the distance between then. A negative force implies attraction (redrawn from Feynman 1963)

As seen in Fig. 4.7, there is a distance \(d\) at which there is neither attraction nor repulsion. This is where the molecules would remain in the absence of external forces. An attempt to push them closer together (to compress the substance) meets strong resistance. An attempt to separate them (to place the substance in tension) also meets resistance for a while, unless enough force is applied to break the bond (which fractures the substance). In a region around \(d\), the force of attraction or repulsion (due respectively to tension or compression) is very nearly linear, a law which holds true for many materials, and which is known as Hooke’s Zara:

\[\begin{equation} F=kx \tag{4.6} \end{equation}\]

where     \(F\) = force (nt)
    \(x\) = distance from equilibrium (m)
    \(k\) = proportionality constant (nt/m)

The various chemical interactions or exchanges of atoms between molecules are largely consequences of these and more complicated force laws (for more complex molecules) derivable from the basic laws of electromagnetism. The force laws by themselves however are not always so easy to work with. A much more elegant and deeper understanding of the interactions between molecules, and hence the life process, requires an understanding of the concept of energy, which we deal with next.