12.7 Heat Gained by Absorption of Radiation

We next consider heat gained by the absorption of radiation including direct solar and sky radiation, reflected solar radiation, and long-wave radiation from the ground and air (Figure 12.3)

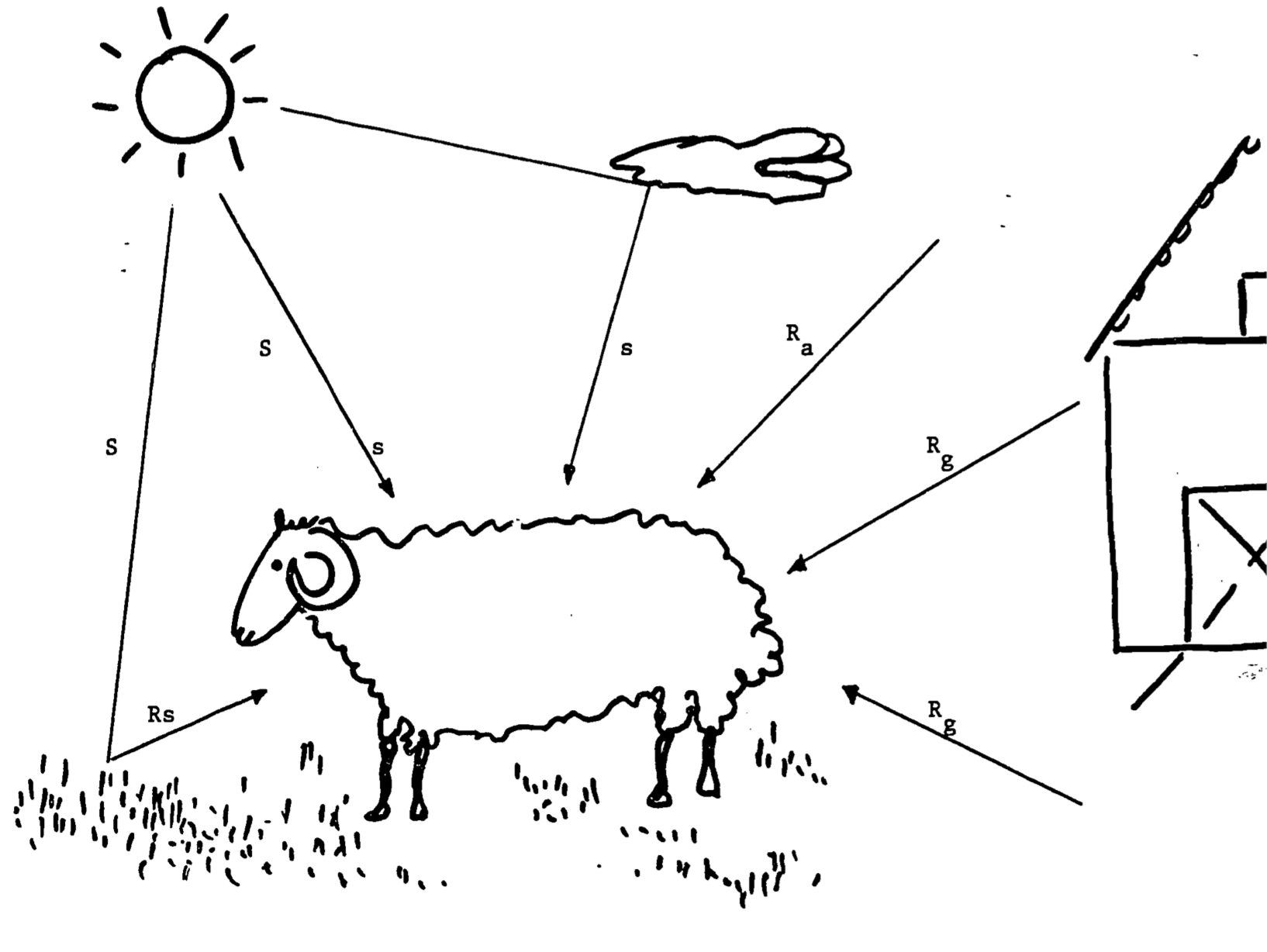
Figure 12.3: Energy gained by sheep from envrionment. Symbols are as follows: S = direct solar radiation, s = sky radiation, $R_s$ = reflected solar radiation; $R_g$, $R_a$ = long-wave (thermal) radiation from ground and air, respectively.

12.7.1 Direct Solar Radiation

We may make an approximate calculation of $a_1A_1S$, the direct solar radiation absorbed by the sheep’s body in unit time, if we consider the amount of sunlight intercepted by a cylinder of diameter $d$ and length $L$. Clearly, if the sun is directly overhead, the shadow cast by the cylinder on the ground has area $dL$. It follows immediately that the surface of the cylinder absorbs the same amount of radiation as would a plane of area $dL$. (The average amount of energy absorbed per unit area of the cylinder is then $a_1 (dL) S/(\pi dL/2) = 2a_1 S/\pi(W m^{-2})$, since the cylinder presents half its area to the sun.) As long as the sheep maintains its body at right angles to the sun, it intercepts the same fraction of incoming solar radiation.

We obtain an estimate of the total direct solar radiation absorbed by the animal by substituting the following values for our parameters:
$a_1 = 0.74$; $A_1 = dL = 0.5\cdot1.0$; and $S = 1046.7 W m^{-2}$, the value corresponding to a clear June 21 day at latitude 40°N at about 10 A.M. or 2 P.M. (Bartlett and Gates, 1967). Then $a_1A_1S = 387 W$.

12.7.2 Sky Radiation

The sheep exposes an area $A_2=\pi dL/2 \;m^2$ of its upper surface (half the area of the cylinder, neglecting the ends) to diffuse radiation coming in from the sky. Then the total sky radiation absorbed is $a_2 A_2 s = a_2 \pi dLs/2$. Since sky radiation intensity is about $27.9 W m^{-2}$ (Bartlett and Gates, 1967), we calculate this component of $A Q_{abs}$ as $(0.74)(\pi\cdot0.5\cdot1.0)(27.9)/2 = 16 W$.

12.7.3 Reflected Short-Wave Radiation

The sheep’s lower surface absorbs direct and scattered solar radiation that has been reflected from the grassy surface on which it stands (Fig. 3). If the grass reflectivity is 0.25 (Monteith, 1973), and if one-third of the solid angle is occupied by the sheep’s shadow, the radiation received will be approximately $(0.25)(2/3)(0.74)(\pi\cdot0.5\cdot1.0/2)(1047.7+27.9)=104W$.

12.7.4 Long-Wave Radiation

The sheep is also heated by thermal radiation emitted from sky ($R_a$) and ground ($R_g$). As Priestley (1957) pointed out, development of a correct model for long-wave radiation absorbed by the sheep is a difficult problem. The major complication arises from sky radiation, which is imperfectly understood. Both Priestley (1957) and Bartlett and Gates (1967) rely on an empirical formula due to Brunt (1939) to calculate sky thermal radiation. Brunt’s formula is $R_a = 1.04 B$ where $B = (0.44 + 0.08\sqrt e)\sigma T_a^4$. In this expression, $e$ is the vapor pressure of the atmosphere (millibars), $\sigma$ is Stefan’s constant ($5.67\times 10^{-8} W m^{-2} K^{-4}$) and $T_a$ is the air temperature (K). Then the sky component of the long-wave radiation absorbed by the sheep is $a_4A_4R_a = 1.04 BA_4$, in which $A_4 = \pi dL/2$. To calculate $B$, we take $e = 10 mb$, and $T_a = 10^\circ C = 283 K$. Then $B = (0.69)(5.67\times10^{-8})(283^4) = 251 W m^{-2}$ and the component due to atmospheric long-wave radiation is $205 W$.

Long-wave radiation from the ground absorbed by the sheep is given by $a_5A_5R_g = A_5\sigma T_g^4$ , where $T_g$ is the ground temperature (K). Here $A_5$ is again one-half the surface area of the cylinder. For our calculation, we will follow Priestley (1957) and make the convenient assumption that $T_g = T_h$, the average temperature of the tips of the sheep’s hair. Since the energy loss from the upper and lower parts of the sheep’s body due to emitted long-wave radiation is $(\pi dL)(\sigma T_h^4)$, the net energy gain due to long-wave radiation is $$1.04BA_4+A_5\sigma T_g^4-2A_5\sigma T_h^4=(\pi dL/2)(1.04B-\sigma T_h^4)$$ Although we have not yet shown how $T_h$ is to be calculated, if we assume again that $T_h=10^\circ C=283K$, then we calculate the net gain as $$(\pi\cdot0.5\cdot1.0/2)(1.04\cdot251-5.67\times10^{-8}\cdot283^4)=-81W$$

Since net gain is negative, we conclude that the animal suffers a net long-wave radiative loss of $81 W$ at its surface.