1.11 Additional Problems
- One way to use least-squares is to approximate one function by another. Here we approximate the curve \[y = 6.1(x+5.0)e^{-0.045x}\] by a straight line \[ y = Ax + B\]
Evaluate both \(\partial (E^2)/\partial A\) and \(\partial (E^2)/\partial B\), then set both equal to zero to obtain two equations in A and B. The goal is to minimize: \[E^2 = \int^{30}_3[6.1(x+5.0)e^{-0.045x}-Ax-B]^2dx\] (Hint: when evaluating \(\partial E^2/\partial A\) and \(\partial E^2/\partial B\), differentiate under the integral sign.)
Solve your equations for A and B and the least squares integral.
- The stomates in leaves are small pores which permit the exchange of gases and water vapor. The stomates change shape from a near circle to a slit in order to adjust this exchange in response to varying environmental conditions. Each stomate is roughly elliptical in shape with constant perimeter throughout the shape change. The area of the opening is then given by \[A= \frac{2b}{a}\int^a_{-a}(a^2-x^2)^{1/2}dx\] where \(2a\), \(2b\) are the lengths of the major and minor axes, respectively, of the ellipse.
First evaluate this integral using either of two trigonometric substitutions: let \(x = a \cos \theta\) or let \(x = a \sin \theta\). Be sure to check the limits on \(\theta\) and the sign of each trig function in the transformed integrand. Your result must be non-negative since the area is non-negative. For a fixed perimeter, say \(35 \mu\), the area should be maximal when the hole is a circle, i.e. \(a=b\). Demonstrate this by evaluating the area when \(a=b=5.57\), and when \(a=5\), \(b=6.09\). (The perimeter formula is \(P = 2\pi\sqrt{(a^2+b^2)/2}\).)
Use your area formula (the answer to part a) to investigate the dilution of the sun’s energy flux due to the angle at which the rays strike the earth’s surface. The dilution is caused by a fixed amount of solar energy being spread over a larger area (as the rays become more horizontal) and thus the energy per unit area decreases as compared to the energy density of vertical rays. The situation is pictured below, giving a top and side view for two inclination angles. The sunlight passes through a circular hole in an opaque sheet and strikes the earth at an angle \(R\) from the perpendicular.
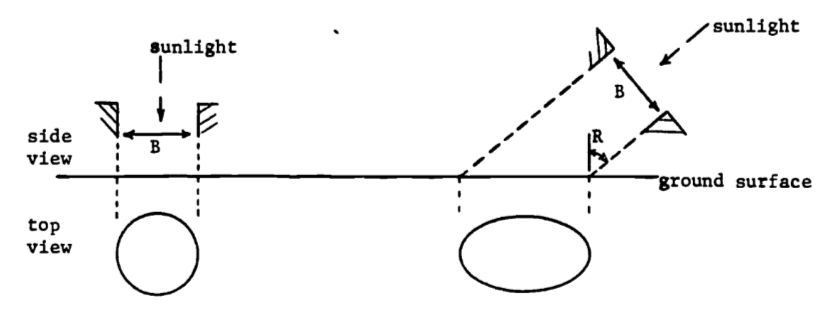
The illuminated area changes from a circle (\(R=0\)) to an elongated ellipse (as \(R\) increases). For a given diameter \(B\), write the illuminated area \(A\) as a function of the angle of inclination \(R\). Check your result by choosing values for \(B\) and \(R\) and calculating the dilution \(D\), which equals the circle’s area divided by the ellipse’s area. Does \(D = 0.6\) mean more dilution (less energy density) than \(D = 0.3\) or vice versa? The inclination angle in Minnesota changes from about 20° in summer to 65° in winter. What is the resulting change in energy density, measured by \(D\)?