4.5 Energy

4.5.1 Work and Potential Energy

Suppose we carry a bucket of water up ten flights of stairs. We would probably all agree that some work had been done. If we had had a course in physics, we would be inclined to say that we had done some work on the bucket of water (as well as on our own selves) in carrying it up ten stories. From our everyday use of the word “energy” we might also note that we expended considerable energy in getting the bucket of water to that great height, and we might intuitively believe that in some way we have imparted some of that energy to the bucket of water, though of course it doesn’t look any different to us from ten stories up as it did at ground level. We will be calling this energy which we endowed to the bucket of water, the “potential energy,” and justify this terminology by noting that if we were to open the window and pour out the water with careful aim onto the blades of a turbine at ground level, the energy of motion (i.e., the “kinetic energy”) which the water builds up as it hurtles turbineward at an acceleration of 9.81 m/sec², will set the blades of the turbine in motion, which in turn will generate several milliwatt-hours of electrical energy. On our return to the ground floor we will no doubt be confronted by the chief physicist of the project who will deprecatingly inform us that though, while we were ten stories up we had a good deal of potential energy ourselves, in walking back down we had lost it all and had effectively performed no net work beyond that which we performed on the bucket of water (or on just the water if we brought the bucket back with us). The water itself, while no longer possessing potential energy, did indeed convert that energy into some useful work in turning the blades of the turbine to produce electricity, but we did no useful work ourselves in descending the ten stories with the empty bucket.

Do physicists and physiologists have different ideas as to what work and energy are? Though it was a lot easier coming back downstairs with the empty bucket than it was going up with the full one, we know that it took some energy expenditure in getting back down the ten flights. And besides, if we had done no net work on ourselves, why do we need the food energy from a bologna sandwich before we can repeat the trip? To understand, we must become precise in our definitions, which we will do on the physicist’s own terms (and which the physiologist will eventually find perfectly acceptable), and then we must bring these into accord with what we know must be true about our own bodily energy expenditure during the round trip.

If we slowly move an object a certain distance in a straight line, and if we must apply a force in the direction we move it (not counting the force necessary to overcome inertia—that’s why we’re moving slowly, so inertial “force” is negligible), the work done on the object by us is defined to be the force we applied, times the distance we moved, thus: \[\begin{equation} W=F_xx \tag{4.7} \end{equation}\] where
    \(W\) = work (joules \(\equiv\) nt-m)
    \(F_x\) = force in x-direction (nt)
    \(x\) = distance (m)

When the distance traveled is great enough that the force is changing as we move the object (such as might be true if we took an object several thousand miles up, so that the force of gravity is diminishing appreciably as we move, or if the object were attached to a spring, where the force is proportional to the distance from equilibrium) we must modify the above definition by summing the infinitesimal amounts of work done in moving the object a series of infinitesimal distances (over each of which the force is essentially constant), which of course is equivalent to finding the integral:

\[\begin{equation} W_{12}=\int_{x_1}^{x_2}F_xdx \tag{4.8} \end{equation}\]

where \(x = x_1\) at the start of our travail, and \(x = x_2\) at the finish. Note that work is done only by that component of the force acting in the direction of motion. Any component for force perpendicular to the motion does no work under this definition.

If the path of motion is not straight, we must give the most general definition of work, which takes the form of a line integral (see Fig. 4.8): \[\begin{equation} W_{AB}=\int_A^BF\cos\theta ds \tag{4.9} \end{equation}\]

where \(ds\) = incremental distance in direction of the path of travel
    \(\theta\) = angle between F and direction of path.

Note that \(F \cos \theta\) is the component of force in the actual direction of motion. Also note that the work done is computed from the force we must apply to the object, not from the force that is opposing our motion. (Otherwise it would have the opposite sign.)

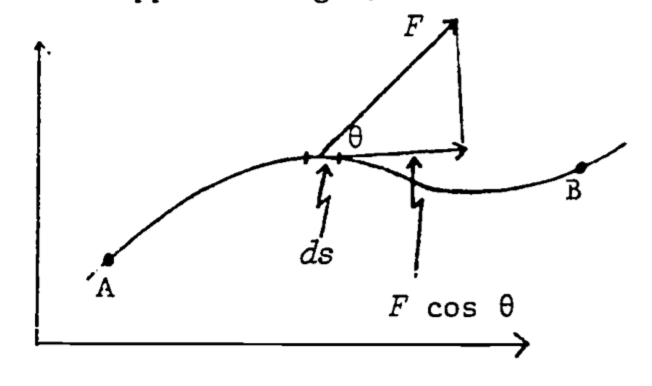
Figure 4.8: Relations between F, \(\theta\), and \(d_s\) used in computing work in moving an object from A to B.

The actual calculation of a line integral is beyond the scope of this module, but this general definition of work is included for completeness.

Let’s use the definition in order to compute the work done on the water in the bucket as we carry it up ten stories to a height \(h\) above the ground. The force due to gravity, which is acting downward on the water (of mass \(m\)), is equal to \(mg\). If we were to carry the water straight up (such as by climbing a vertical ladder) we would be applying an upward force mg, in the direction of motion. Thus the work we do on the water is force times distance, or: \[\begin{equation} W=mgh \tag{4.10} \end{equation}\]

What if, instead of climbing a vertical ladder, we had carried the water up a plane inclined at the angle \((\phi)\) (Fig. 4.9)?

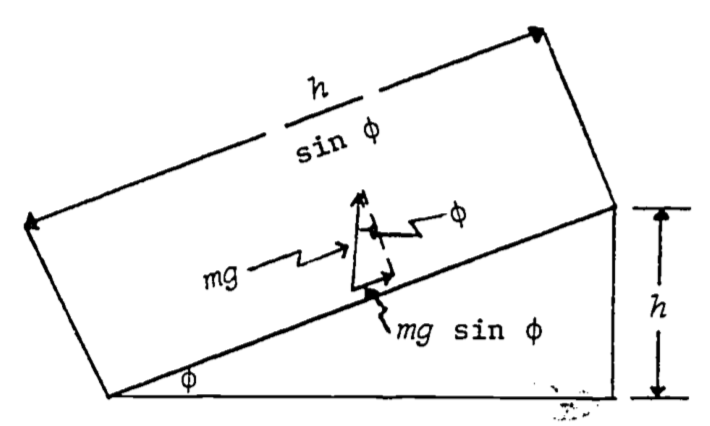
Figure 4.9: Relations between quantiles needed to calculate work against gravity on an object being taken up an inclined plane.

The vertical force we apply to the water is \(mg\), while the component of force acting in the direction of motion is \(mg \sin\phi\). The distance the water moves under this constant force is \(\frac{h}{\sin\phi}\). Consequently the work is: \[W=mg\sin\phi\frac{h}{\sin\phi}=mgh\] The same as before! This is no accident. In fact, it is not difficult to see that the amount of work done on an object in raising it a height \(h\), by any path, will always be \(mgh\). (Imagine an arbitrary path from the ground to height \(h\) to be approximated by an interconnected collection of infinitesimally short straight line segments, the \(i^{th}\) one of which is tilted at an angle (\(\phi_i\) and rising an amount \(\Delta h_i\) over its length. The total work is thus \(\sum mg\Delta h_i = mgh\).) When a force law has the property that the work done on an object in moving it from position A to position B is the same no matter which path we take in getting from A to B, we call, the force conservative. A corollary of this is that under a conservative force, a round trip from A to B and back to A again results in no net work being done. For if there were net work done in the round trip ABA, then all paths from A to B would not result in the same amount of work (since ABAB and AB are both legitimate paths from A to B, with the former clearly requiring more or less work when the round trip is thrown in).

When the force is conservative (as we have just shown to be true for a force which is constant in both magnitude and direction), then for an object of mass \(m\) each point in space will possess a unique value for the work required to move the object to that point from some constant reference point. This value of work is unique in the sense that no matter which path were chosen to get from the reference point to the position in question, we would do the same amount of work on the object. Of course if we shift the reference point, we may change the value of work in getting to the position in question. So when we pick a reference point, let’s not change it. We may now regard an object of mass m at some position in space as possessing the property that a certain amount of work has been (or could have been) done on it in getting it from the reference point to where it is now. However, we don’t usually call this property “work” (since “work” is an action). Instead, we refer to this property as the potential energy of the object with respect to the reference point. Thus the potential energy of an object is the amount of work that would have to be done in taking the object from the reference point to its present location. To put it another way, the potential energy is the amount of work that the object could perform on something else in making its own way back to the reference point. Energy obviously has the same units as work (joules)—the two words are distinguished by our perception that “potential energy” is a property possessed by a body (as a consequence of its position in space) which would enable it to perform an act called “work.”

The importance of our peculiar definitions of work and energy lies in the profound fact, which we will demonstrate subsequently, that under conservative force laws, the total energy of an isolated system remains constant. There may be exchanges of energy between certain parts of the system or there may be changes in form of the different energies (e.g., potential energy may be changed into the energy of motion), but the sum of all the component energies of the isolated system must remain forever constant.

Energy is recognized in several different forms, each associated with a different force law, and each expressed by a different formula. The different forms of energy we recognize are gravitational, kinetic, heat, elastic, electrical, chemical, radiant, nuclear, and mass-energy. Since there are only four basic force laws (taken in conjunction with Newton’s second law), there is obviously some redundancy in this list. For example, what we call “heat energy” is in fact a manifestation of the “kinetic energy” (energy of motion) of the molecules of a substance.

Since the law of conservation of energy depends on the forces being conservative, it is well to ask whether the four basic force laws are conservative. They are indeed. There are no non-conservative forces! There are, however, some apparent non-conservative forces, such as friction. For example, if we slide an anvil from Dubuque to Peoria, the amount of work we do depends on which highways we slide it on. And surely if we make a round trip, we will do significantly more than zero work in getting back to Dubuque. Thus certainly our energy is not conserved. However, if we look at things more closely, we will discover that that work we did on the anvil, though not resulting in any potential energy gain by it, did result in setting a number of molecules in both anvil and highway in much more rapid motion. Our work went into heating the highway and the anvil, that is, increasing the kinetic energy of their respective molecules and hence, increasing the temperature of both road and anvil– it didn’t result in what we think of as useful work, but neither did it result in a loss of energy to the universe.

If you are wondering whether this work against friction can be recovered to perform work on something else, that is, if we could use the enhanced kinetic energy of the Molecules of the anvil and the highway to do work, the answer is we could use some of it, but not all. A good deal of this energy will be forever unavailable to do work, which we will see later is a consequence of the second law of thermodynamics and which we shall have to elaborate upon in terms of what we call the “entropy” and “free energy.”

We can now begin to understand some of the differences between “physical work” (as defined by Equation (4.9) and “physiological work,” such as we do when we run downstairs, or hold a heavy weight in a stationary position. In running downstairs, or at a constant level, though we’re doing negative, or at best zero work against gravity, it seems apparent that we’re doing considerable work against friction. Some of this results in a direct heating up of the environment—the air molecules we bump into are sped up, the molecules of the earth under our feet are given a jolt with each stride—but more significantly, there is a good deal of friction within our bodies as we run, many parts sliding and rubbing each other as our muscles contract and extend. We might think that since this energy remains within the body, in the form of kinetic energy, that it’s not lost to us—we should still be able to get some useful work out of it. Again, the second law of thermodynamics denies this possibility for the most part, saying that we cannot get useful work solely by extracting energy from the kinetic energy of a randomly moving, i.e. disordered, array of molecules. Thus, since the body cannot make good use of this energy, it must release most of it, or else this kinetic energy will result in a disastrous rise in body temperature. Consequently, water is made to appear on the surface of our skin through the pores (i.e., we sweat) and as we learned previously, the more highly energetic of these water molecules will depart, leaving behind the slower ones. And the body cools.

But there’s more to the explanation of physiological work than just external and internal friction. For imagine that we’re not running, but instead are standing as still as we can, while holding an anvil at chest height. There is no physical work being done, but there certainly is some physical exertion! If we were to set the anvil on a table, we know that neither physical work nor physical exertion would be required of the table. Why must we work so hard to do no physical work? The answer lies in the way our striated or skeletal muscles function.

Muscles consist of interdigitating protein filaments that slide past each other (Figs. 4.10 and 4.11).

Figure 4.10: Muscle at rest.

Figure 4.11: Muscle contracted.

The energy which makes muscles contract comes mostly from the chemical energy stored in the molecular bond of a class of compounds called phosphagens, the most noteworthy of which is adenosine triphosphate (ATP). The ATP will release its energy in the presence of calcium ions, which are stored away from the ATP in a system of tubules (the sarcoplasmic reticulum) in the muscle cell. When an electrical signal from the nerve is delivered to a muscle fiber, the calcium ions in the sarcoplasmic reticulum are released into the fluid surrounding the muscle filaments. The ATP molecules present on these filaments release their chemical energy (by which we really mean electrical potential energy) and the muscle contracts, or at least attempts to. The calcium ions are immediately pumped back into the sarcoplasmic reticulum, and in fresh muscle, new ATP is created from another phosphagen present in muscle cells, which ultimately must get its energy from the oxidation energy available from food combustion. These processes all happen in a matter of hundredths of a second, after which the muscle cell relaxes. So what we actually see upon the electrical signal from the nerve, is a twitch in the muscle fiber! For us to lift and hold a constant load, say the weight of an anvil, there must be many twitches per second—the nerves are constantly firing, and ATP is constantly discharging its energy and re-energizing. It can do so only as long as the blood can resupply the energy to the muscle from that energy available from food consumption. Under heavy exertion the energy from food consumption cannot be delivered fast enough to the muscle, and the load must be dropped or the running stopped for want of ATP. (As you might guess, there’s more going on than just this, but these are the essential features.)

It seems strange that nature should have evolved such an inefficient scheme for muscle action, but apparently this is what we must give up in order to have “fast” muscle. Nature seems to have been unable to have evolved muscle which can act rapidly and also sustain large static loads. The smooth muscle (such as that surrounding the intestines) is built quite differently, and acts much more like the table in holding a constant load, where the molecules essentially lock into position to sustain that load. The abductor muscle of the clam represents a good example of smooth (hence “slow”) muscle which can effortlessly sustain a load over long periods.

4.5.2 Kinetic Energy

We must now formally obtain a formula for kinetic energy, which is defined to be the amount of work we do in overcoming the inertial force of a body of mass \(m\), in getting it from zero velocity to a velocity \(v\). The inertial force is given by Newton’s second law, which we manipulate a bit using the chain rule for derivatives and recalling that the rate of change of velocity is acceleration: \[F=ma=m\frac{dv}{dt}=m\frac{dv}{dx}\frac{dx}{dt}=mv\frac{dv}{dx}\] We may insert this into the definition of work (Equation (4.8)) to get: \[\begin{equation} \mbox{Kinetic Energy}\equiv T=\int mv\frac{dv}{dx}dx=\int_0^vmvdv=\frac{1}{2}mv^2 \tag{4.11} \end{equation}\] We are now ready to establish the law of conservation of energy, which we do forthwith.

4.5.3 Conservation of Energy

It’s interesting to note that this cornerstone physics, the principle of conservation of energy, was first demonstrated by the German physician, Dr. Julius Robert Mayer, based on his observation that the venous blood of a patient in the tropics is redder than the venous blood of a patient in the temperate zone. This difference, he concluded, resulted from the body’s lower oxidation rate required to maintain body temperature in the tropics: Mayer viewed the organism not as an independent entity, but as a part of the environment and responsive to its external surroundings, which led him eventually to an understanding of the mechanical equivalent of heat, and ultimately to a statement of the law of conservation of energy, which he published in 1842 in Liebig’s Annalen on “The Forces of Inorganic Nature.” Thus did biology make a signal contribution to physical theory.

The principle of conservation of energy is simply stated:

In an isolated system, the total energy never changes.

This is to say that if we are careful not to let anything bump into our system (such as air molecules), and if we keep it hidden from sources of radiant energy (such as the sun), then whenever we measure the kinetic and potential energies of the system’s component parts, and add them up, we will always come up with the same answer.

For a single body acting under a conservative force, we may write one statement of the principle of energy conservation: \[T + V = \mbox{constant}\]

where \(T\) and \(V\) are the respective kinetic and potential energies. A falling body, e.g., would every second be “losing” potential and “gaining” kinetic energies, but the total at any time is constant.

Let’s see if this relationship holds in the case of a body of mass \(m\) falling freely in a gravitational field (neglecting frictional losses due to collision with air molecules). In such a case we would have:

\[\begin{equation} \frac{1}{2}mv^2+mgh=\mbox{constant} \tag{4.12} \end{equation}\]

If equation (4.12) is true then the time derivative of the left hand side must be zero. Taking this derivative: \[\begin{align*} \frac{d}{dt}(\frac{1}{2}mv^2+mgh)=\frac{1}{2}m\frac{d}{dt}(v^2)+mg\frac{dh}{dt}&=\frac{1}{\rlap{---}2}m\rlap{---}2v\frac{dv}{dt}+mg\frac{dh}{dt} \\ &=mv(-g)+mgv=0 \end{align*}\]

where we have chosen the positive direction for \(h\) to be upward, \(\frac{dh}{dt} = v\) (both \(\frac{dh}{dt}\) and \(v\) are negative), and the acceleration due to gravity \((\frac{dv}{dt} = -g)\) is a negative quantity since it is directed downward. Thus, the derivatives of both sides of (4.12) are zero and (4.12) is satisfied. We also interpret this to mean that the principle of conservation of energy is satisfied.

To show that conservation of energy holds in general is best done using the tools of vector analysis, which is beyond the scope of this module. It is easy to show without vector analysis that it must be true for an object moving in a straight line. Then if you’re satisfied to think of an arbitrary curved path as being made up of infinitesimal straight line segments, you will be satisfied with the following:

All that need be done is to return to the development of the formula (4.11) for the kinetic energy, which was defined as the work necessary to get a body from zero velocity to a velocity \(v\). If we wish to find the work done on the body in getting from a velocity \(v_1\) (at point 1 in space) to a velocity \(v_2\) (at point 2 in space), the steps are the same as in obtaining equation (4.11) except the final integral has limits \(v_1\) and \(v_2\):

\[\begin{align} \mbox{Work in getting from 1 to 2} \equiv W_{12}&=\int_{v_1}^{v_2}mvdv \notag \\ &=\frac{1}{2}m(v_2^2-v_1^2) \notag \\ &=T_2-T_1 \tag{4.13} \end{align}\]

Equivalently, if the force acting on the body is conservative (work done is independent of path from 1 to 2), then we may figure out a potential energy (relative to an arbitrary point) of the body at each point, say and the work we must do \(V_1\) and \(V_2\), on the body in getting it from 1 to 2 is \(V_2 - V_1\). If we release the body at point 2, the force associated with the p(potential (let’s say it’s gravity) will do en amount of work \(W_{21} = V_2 - V_1\) on the body in getting it from point 2 to point 1. We may write:

\[\begin{equation} W_{12}=-W_{21}=V_1-V_2 \tag{4.14} \end{equation}\]

Comparing this to equation (4.13) gives us the statement of conservation of energy: \[V_1-V_2=T_2-T_1\] or \[\begin{equation} T_1+V_1=T_2+V_2=\mbox{constant} \tag{4.15} \end{equation}\]

since points 1 and 2 were arbitrary.

The principal assumption in this development is that the forces acting on the body are conservative, which we reiterate is true for all four known basic force laws, but which is not necessarily true for other so called forces such as friction. Thus, when we employ the conservation principle, we must be sure that the system we have in mind is isolated, or else we must account for exchanges of energy between the system and its surroundings. Conservation of energy is a universal principle, but it works only if we have accounted for all possible exchanges of all possible forms of energy. We will discover that the laws of thermodynamics provide a most convenient tool for dealing with these exchanges.

In passing, we point out one more assumption made in the development of the law, which though not of professional interest to biologists, should be of some philosophical interest. In the development of the expression for the kinetic energy, the mass of the object was assumed constant. In everyday circumstances this is true, but as you’re no doubt aware, at velocities near the speed of light it is not true. When Einstein used his formula for mass as a function of velocity in the development of an expression for kinetic energy, he discovered that in order for the formulation to be consistent with conservation of energy, a net change in mass in an isolated system would be associated with a net opposite change in energy of magnitude \(E = mc^2\), where \(m\) is the change in mass and \(c\) is the velocity of light. This is the form of energy previously referred to as mass-energy, and is of utmost importance to the under standing of nuclear reactions, though it won’t concern us further here.

4.5.4 Gravitational and Electrostatic Potential Energy

We can now establish formulas for gravitational and electrostatic potential energy. For reasons that will become apparent in the development, we usually choose \(r = \infty\) to be the reference point for the potential energy; that is, we shall define \(V_{\infty} = 0\). Thus if we take equation (4.14) and (4.8) in combination to define potential energy, then substitution of equation (4.2), Newton’s law of universal gravitation, into the defining potential energy relations gives: \[\begin{align*} V_r-V_{\infty}&=-\int_r^{\infty}g\frac{Mm}{r^2}dr \\ V_r&=-G\frac{Mm}{r} \tag{4.16} \end{align*}\]

where
    \(M\) = mass of earth
    \(m\) = mass of object whose energy we’re computing
    \(r\) = distance from center of earth

The negative sign is taken since the force is opposite to the positive \(r\) direction. Since we expect that an object loses gravitational potential energy as it falls closer to the center of the earth, and since we defined \(V_{\infty} = 0\), then we should expect \(V_r\) to be able to take on only negative values, and to be getting more negative as \(r\) becomes smaller. You may object that Newton’s law of gravitation applies only to point masses (or infinitesimal masses) and that an accurate expression for the potential energy of an object at a distance \(r\) from the center of the earth could only be obtained from an integral over all the infinitesimal volume elements of the earth. Gauss, however, in a beautiful theorem, demonstrated that one could treat a spherical object as though all its mass were concentrated at the center, and get the exact answer that one would get by performing the complicated integration!

We have derived two different expressions for the potential energy in a gravitational field, which may have led to confusion. In the first case, we made the assumption that we were raising an object to relatively low heights (say no more than a few miles) over which distance the force of gravity could be considered constant. It was most convenient to consider the earth’s surface as the zero reference point for computing the potential energy. In the second case we used the more accurate expression for the gravitational force, the form of which led to infinity as the most convenient reference point for computing potential energy. Since in any practical situation we will only be interested in change in potential energy, the choice of reference potential energy is immaterial, because no matter what reference point is chosen, the calculated change in potential energy between two points will always be the same. We must not, however, change reference points in the middle of a calculation!

To demonstrate the power of the principle of conservation of energy, let’s compute the “escape velocity” from the earth’s gravitational field. Escape velocity will be defined as the velocity at which we must propel an object so that at a large distance the object is just barely moving. Thus at a great distance both the potential energy and kinetic energy will be zero. At the earth’s surface, the total energy must therefore also be zero, allowing us to write: \[\frac{1}{2}mv^2-G\frac{Mm}{R}=0\] where \(R\) = radius of earth.

Thus the escape velocity is \(v = \sqrt{\frac{2GM}{R}}\).

Of greater biological importance is the potential energy associated with the electrostatic force. Since, like gravity, it is an inverse square law, there is no need to derive it again, but rather just write:

\[\begin{equation} V=\frac{1}{4\pi \varepsilon_o}\frac{q_1q_2}{r} \tag{4.17} \end{equation}\]

where once again infinity is chosen as the reference point. The sign is positive since, unlike gravity, the force between like charges is repulsive. (Of course, if the charges are unlike, we would come up with the negative energy associated with attractive forces.)

With the background that we’ve now gathered, we are ready to begin a discussion of the application of the principles we’ve developed to the study of thermodynamics, which we will find to result in a most elegant set of tools for the handling of some otherwise vexing, but nonetheless important, biological problems.