13.7 Problem Set

1. Verify that:
   1. Equation (13.11) is a solution to Equation (13.8).
      
   2. Boundary conditions 9 and 10 satisfy Equation (13.8).
2. Devise an expression for surface heat flux density $(G(0))$ from Equation (13.11).
   1. What is the maximum heat flux at the surface? Hint: The trignometric identity $\sin(x+y) = \sin x \cdot \cos y + \cos x \cdot \sin y$ may be useful.
      
   2. When does the heat flux reach its maximum in relation to the maximum in the diurnal temperature wave at the surface? The annual temperature wave?
      
   3. Show that the quality $D/\sqrt{2}$ can be regarded as an “effective depth” for heat flow. Hint: Compare Equation (13.2) with result from part 2(a).
      
   4. Show that the amount of heat flowing into the soil during one-half cycle is $\sqrt{2}CDA(0)$. This is the amount of heat required to raise a layer of soil $D/\sqrt{2}m$ thick $A(0)$°C.
3. Refer to Figure 13.2.
   1. Derive an expression for the damping depth $D$. What is the value of $D$ for the diurnal temperature wave? What is the functional relation between the diurnal and the annual damping depth? What is the value of the annual damping depth?
      
   2. Estimate $A(0)$.
      
   3. Calculate diffusivity $(K)$. Was the soil wet or dry (see Table 13.1, or Figure 13.15 in problem 4)?
4. Based on the following figure, comment on possible explanations for the shape of the curves. Hint: Compare Figures 13.6 and 13.7.

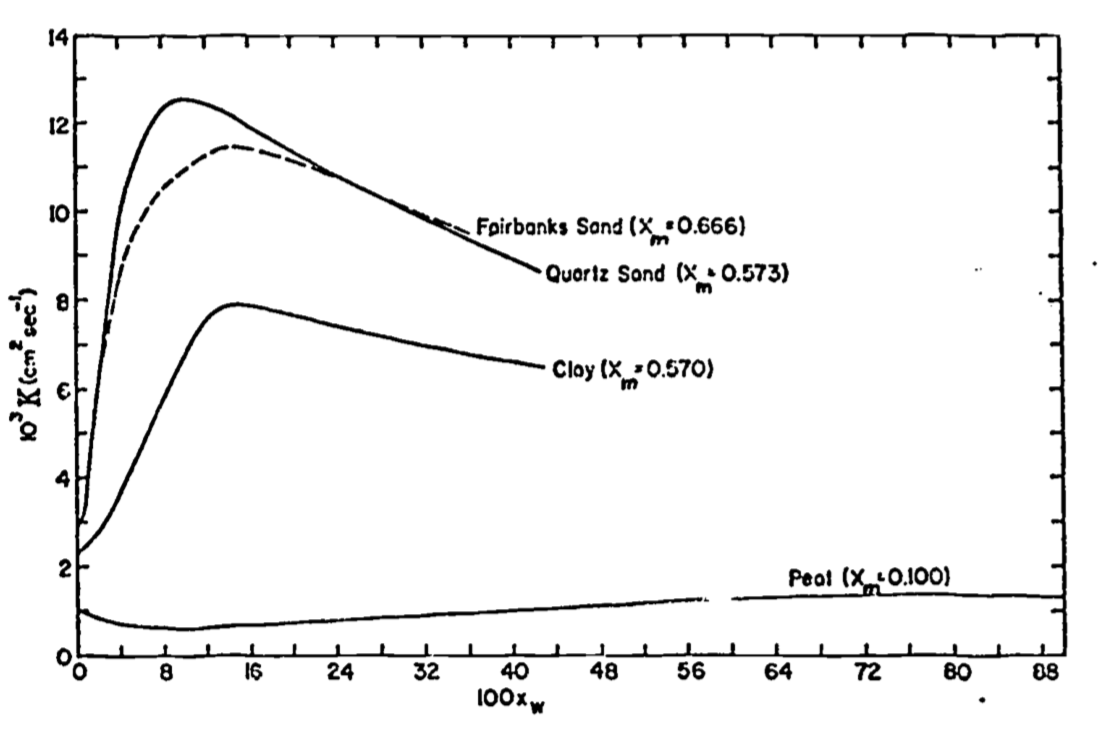
Figure 13.15: For problem 4